집밖은 위험해

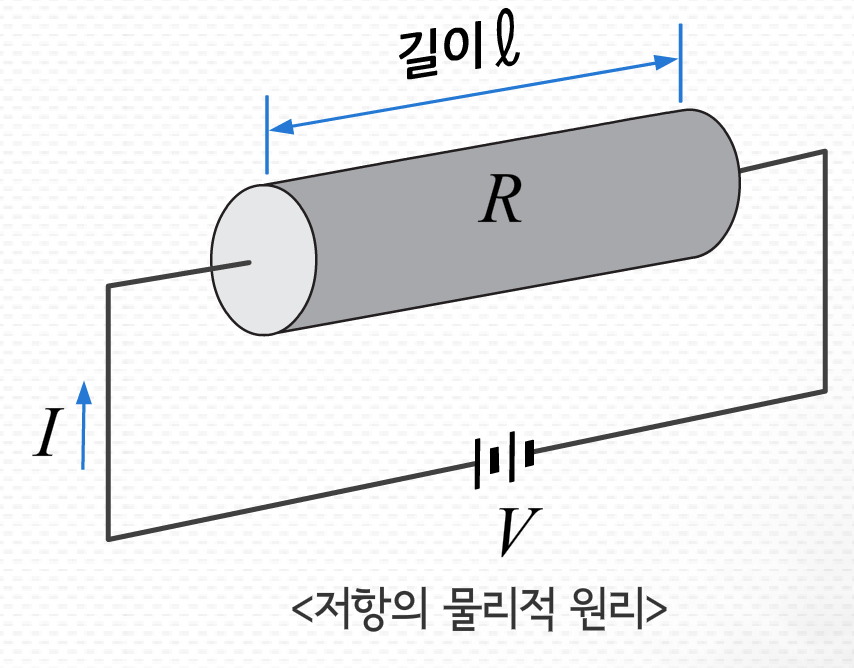
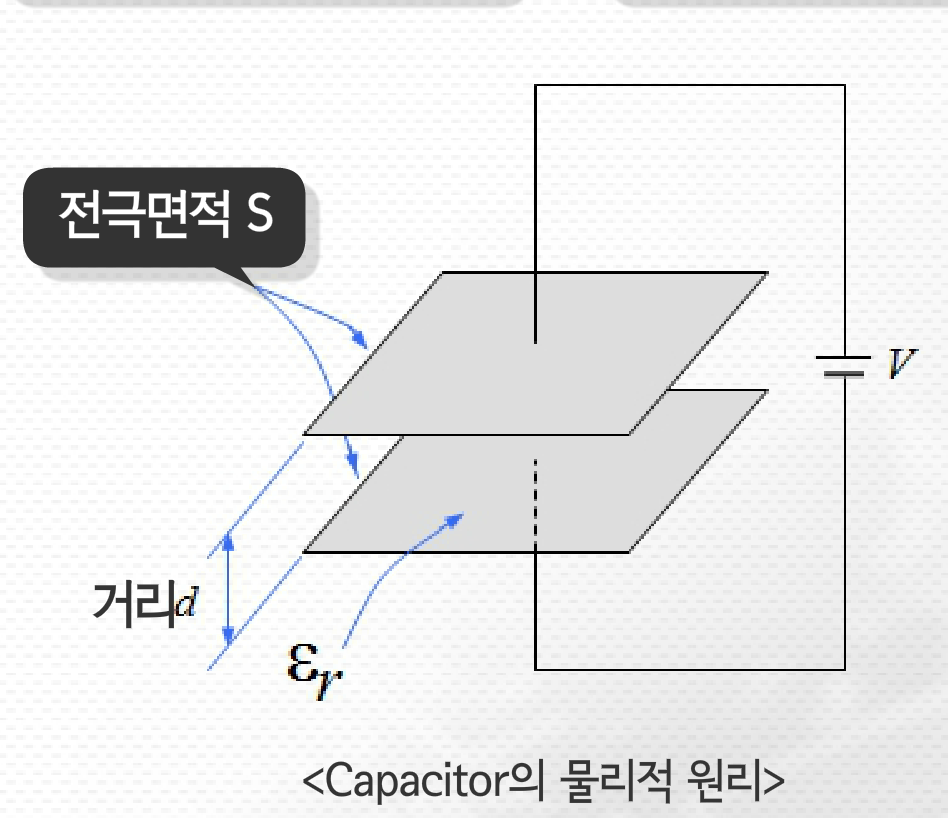
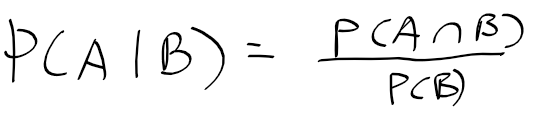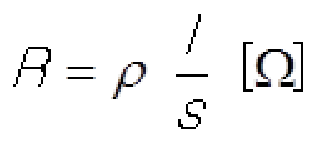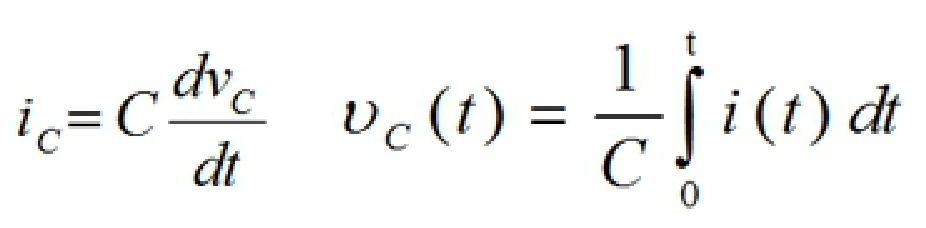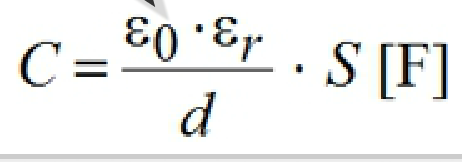 기후 변화, 방사능 유출같은 세계적인 문제들로 인해, 그리고 에너지 소모를 줄이기 위해 많은 공학자들이 세로운 제어기 설계 방법을 찾으려고 노력하고 있습니다.

 그러한 설계 방법을 그린 엔지니어링 green engineering이라고 부르며, 그린 엔지니어링의 목표는 오염을 줄이고, 사람에게 유해를 줄이도록 하는 제품을 만드는것이 목표라 할수 있겠습니다. 이러한 그린 엔지니어링의 원칙에 따라서 피드벡 제어 시스템의 유용함을 보여드리고자 합니다.

 지구 온난화 문제와 오염을 줄이기 위해서는 환경 모니터링 시스템을 늘리고, 품질도 높여야만하는데요. 한 가지의 예시로 외부 환경을 관측하는 무선으로 이동하면서 감지하는 플랫폼들이 있습니다. 보내지는 전력과 전압의 변화 등을 측정하는것도 그러한 예시라고 할수 있겠습니다.

 수많은 그린 엔지니어링 시스템들을 다루기 위해서는 신중하게 전류와 전압을 보아야만 하는데요. 전력 변환기는 전력 공급망 상에서 흘러가는 다양한 크기의 전류를 측정하고 모니터링을 할수 있어야 하며, 여기서 사용되는 센서들은  측정치가 제어 시스템이 적절한 동작을 하는데 필요한 정보들을 제공하므로 제어 시스템의 핵심 요소라고 할수 있습니다.

 그린 엔지니어링에서의 제어시스템의 역활은 자동화와 정밀화 수준이 높아만 가면서 세계적으로 큰 역활을 하게 될겁니다. 그래서 이후에는 풍력 발전기같은 그린 엔지니어링의 제어나 태양의 밝기가 변화하는 사이에서도 전력 생산량을 최대로 하는 태양광 발전기 피드벡 제어 시스템을 설계해보겠습니다.

 제어 시스템으로 개발할수 있는 다른 재밌는 것으로 IoT가 있습니다. 여기서 IoT란 Internet of Things의 약어로 많은 전자 장치들이 연결된것을 말합니다. IoT 네트워크 상에서 수백만의 장치들은 각자의 컴퓨터가 내장되어 인터넷에 연결 됩니다. 이러한 연결된 장비들을 제어해보는것은 제어 공학도에게는 신나는 일이라 할수 있을것 같습니다.

 그래서 제어 공학은 재미있고, 도전할만한 분야라고 생각합니다. 제어 시스템은 본래 여러 분야가 혼합된 학문으로, 엔지니어링 커리큘럼 상에서 핵심역활을 한다고 할수 있겠습니다. 이 분야에서는 수학적 배경 지식이 많이 필요하므로, 정리와 증명과 같이 이론적인 부분들도 다루긴 할겁니다. 하지만 최종 목표는 현실에서 동작가능한 제어기를 설계하는 것이므로, ad-hoc(임기 응변)적인 방법과 직관력으로 피드백 제어기를 설계해 보겠습니다.

 앞으로 배우는데 있어서 가장 중요한 것은 과거에 다루었던 문제와 이에 대답을 다시 찾아보는것이라 할수 있겠습니다. 그래서 학생들이 수많은 문제들과 해결방안 그리고, 수십년 전에 있어왔던 해결 방안에 대해서 배워보아야 합니다. 옛날의 학습 방법에서 학생은 이러한 문제를 고민하지 않고 단순히 과제들을 풀기만 했었습니다. 하지만 이 과정을 통해서 배우는 사람들이 이론적인 어려움을 줄이고 창의성과 즐거움을 찾길 희망하고 있습니다.

 이제 피드벡 제어 이론의 구조에 대해서 살펴보고, 다양한 흥미로운 주제들을 드리고자 합니다. 그래서 여러분들이 피드벡 제어 시스템 이론과 실습에 도움이 되었으면 좋겠습니다.

확률 변수 random variable

- 관심 사건을 변수로 설정한 것

 => 확률 변수 X = 0, 1, 2, 3 중 하나의 값 -> X = 1, X = 2와 같이 표현

확률 분포표

- 확률 변수의 값과 그에 대한 확률을 나열한 표

이산 확률 변수 discrete random variable

- 확률 변수가 정수와 같이 셀수 있는 값을 가지는 경우 이산확률 변수라 부름

 => ex. 동전 앞면 수, 오타 수, 합격자 수 등

이산 확률 분포

- 이산 확률 변수에 대한 확률들의 분포

- 아래는 동전 2개를 던질때 앞면이 나온 수에 대한 이산 확률 분포

확률 질량 함수 probability mass function, pmf

- 각 확률 변수에 대한 이산 확률들, P(X=x_i) = p_i가 확률 질량 함수 pmf

연속 확률 변수 continuous random variable

- 확률 변수가 셀수 없는 경우 연속 확률 변수라 부름

 => ex. 시간, 무게 등

확률 밀도 함수 probability density function, pdf

- 어느 확률 변수가 어느 구간에 속할 확률을 결정짓는 함수

 => [1, 2]에 속할 확률, [1, 3]에 속할 확률 등

 기대값 expectation value

- 확률 변수 x_i와 해당 확률 p_i의 곱들의 합으로 시행시 기대되는 결과를 예측할 수 있음

복권 예제에서의 기댓값

- 복권을 뽑을때 받을수 있는 상금에 대해 아래와 같은 확률분포표가 제시된다고 하자.

- 한번 복권을 뽑는 경우 예상되는 상금은 다음과 같다.

 => 기대값 E(x)는 한번 시행시 예상 결과로 이 경우에는 12원의 상금이 기대된다.

분산 variance

- 확률 변수가 기댓값을 중심으로 얼마나 퍼져있는지 정도

- 기대값 E(x) = mu로 표기하나 mu가 음수인 경우도 존재하므로

 1. 확률 변수 X와 기대값 mu의 차이를 제곱

 2. 차이의 제곱에 대한 평균을 구함

표준 편차 standard variation

- 분산 Var(X)는 차이 제곱에 대한 평균을 구하므로 기존의 확률 변수 X와 단위가 다름

 => 단위 일치를 위해 제곱근을 수행하여 구함

조건부 확률 conditional probability

- 정보가 주어졌을 떄 어떤 사건이 발생할 확률

주사위와 조건부 확률 - 상황

- 주사위 던질때 1의 눈이 나올 확률 1/6

- 짝수가 나올 확률 1/2

주사위와 조건부 확률 

- 주시위가 3이하라는 정보가 주어짐. 짝수일 확률은 몇일까? 여전히 1/2?

- 위 경우 짝수인 경우는 세가지 중 하나

 => 3 이하라는 정보가 있을때, 짝수일 확률은  1/2(전체의 절반)가 아니라 1/3(3이하 수중 하나)

조건부 확률

- 주어진 정보로 사건 B가 발생하였다는 가정하에 사건 A가 발생할 확률

베이즈 정리

- 조건부 확률을 이용해 어느 사건의 발생 확률을 구하는데 사용되는 정리

베이즈 정리의 예시 - 공장

- 생산 라인 1(생산률 20%, 불량 비율 5%), 생산 라인 2(생산률 50%, 불량 비율 4%), 생산 라인3(생산률 30%,불량률 3%)

=> 문제 : 1) 전체 불량률은 몇일까? 2) 불량품이 첫 라인에서 만들어질 확률은?

전체 불량률

- 생산 라인 1 : 0.2 x 0.05 = 0.01

- 생산 라인 2 : 0.5 x 0.04 = 0.02

- 생산 라인 3 : 0.3 x 0.03 = 0.09

=> 전체 불량률 = 0.39

표본 공간 분할과 사건 A

- 표본 공간 S는 분할된 사건 B1, B2, B3, B4로 구성

사건 A가 주어졌을떄 조건부 확률

- 사건 A에 대한 정보가 주어진 경우, 사건 B_i에 대한 조건부 확률

베이즈 정리 bayes theorem

- 표본 공간을  B1 , ... Bk로 나눌 경우 사건 A와 조건부 확률 B_i는 아래와 같다.

    => 베이즈 정리 : 사전 확률과 분할 사건에 대한 사후확률을 구하는 아래의 식

베이즈 정리를 이용한 전체 불량률 구하기

- 전체 불량률 P(A)은 얼마나 되는가?

1. 사건 정의

- B1 : 제품이 생산 라인 1에서 만들어질 사건

- B2 : 생산 라인 2에서 만들어질 사건

- B3 : 생산 라인 3에서 만들어질 사건

2. 우도 likelihood 정리

- 각 라인에서 생산한 제품이 불량률일 확률

3. 베이즈 정리로 구한 전체 불량률

- 베이즈 정리로 사후확률과 사전 확률은 아래와 같이 정리할 수 있다.

- 지금 구하고자 하는것은 전체 불량률, 즉 사후확률 P(A)를 구하므로 다음과 같이 정리된다.

4. 베이즈 정리로  불량 제품을 뽑앗을때 1번 라인에서 생산한 제품일 확률

애매한 재능, 어중간한 재능은 잔인하다는 말이 종종 보인다.

그럴수 밖에 없는게

아예 못한다면 포기하면 되지만

어중간한 재능을 갖고 있으면 머리가 나쁜것 가지는 않고

미련을 남기게 되고

수렁에 빠지게 만드는 원인이 된다.

아주 뛰어난 사람이 많은데

어중간한 재능으로 뛰어드는 건 정말 힘든 일인것 같다.

본인도 그런 점에서는 어중간한 재능을 가졌다고 생가간다.

모르는 사람이 보는 입장에서는 대단해 보일수 있어도

대학원 연구원들이 보면 그렇게 잘한것 같지 않아보일것같다.

학회에서 갔을때도 비전공자여서인지는 모르나 다른 대학원 생들에 비해 매우 못미치는 정도의 연구밖에 하질 못하다보니

내가 어중간한 재능을 가졌다고 생각을 강하게 하게되었다.

그런 탓에 뛰어난 사람들을 이기기 보다는 내 강점을 찾기 위해

다방면을 다루는데 집중하다보니

현 블로그처럼 이내용 저내용을 정리하게 되기도 했다.

유튜브보니 이런 내용들이 참많더라

어중간한 재능이 있는 사람들에게 잘 모르는사람이 함부로 부추기는건 참 무책임해보인것같기도하다.

오마르

오마르님도 비슷한 고민을 하셨더라

랩에 대해서 주변인들의 칭찬을 듣다보니 잘하는줄 알았으나

결국 본인은 빈지노가 아니었고

20대를 많이 소모하게 되었다고 한다.

한편으론 애매한 재능을 축복이라고 말하는 사람도 있다.

https://jiyoonpyo.tistory.com/22

내가 애매한 재능을 가졌는건지

노력을 하지 않아서인건지

고민이 된다면

나는 전자라고 생각된다.

이전에 수능때 죽기살기로 공부했지만

결국 3~4등급대에서 정체되어 몇달동안 성적이 오르지 않았던 적이 있었다.

수능, 평가원 등의 성적에서 상위 20~25%정도인 중상이었으니 못한다고는 할수 는 없었으나

10%를 넘어가는덴 분명히 한계가 존재했다.

지금 보면 내가 내 생각에만 빠져 좁은 시야에서 공부했기 때문이라 판단하고

가능한 넓은 시야를 가지려고 다른 사람들의 공부 방뻡, 조언 등을 찾으려고 의식적으로 훈련 중이긴 하다.

덕분에 내가 할수 있는 일의 범위는 늘어나기는 했으나

20%대의 한계를 넘기기는 힘든것같다.

애매한 재능을 갖고 한 분야의 탑이 되는건 미련이고 괴로운 일일것 같아.

내 생활을 다채롭게 만드는게 중요하다고 생각된다.

지금처럼 다양다양하게 하다보면

한 분야만 파고들었을때 보지못햇던 통찰력을 얻고

한 분야만 팟을때 20%였다면

타분야를 통해 통찰력을 얻고 1%, 2% 정도 조금씩 성장하는게 목표다.

평생 공부만 하고 살순 없으니

현실과 이상을 잘 조절하면서 생할하고는 있는것 같지만

언제까지 공부만 해선 안다고 생각은 하고있긴하다.

대강 대학 수학 범위의 절반 정도는 본것같다.

확률도 비슷하게 정리하고

통계도 얼른 시작해서 마무리해버려야 z

1. 미분

미분 derivative

- 변화하는 정도. 즉, 기울기

평균 변화율 average rate of change

- y = f(x)가 주어질때 x = $x_0$, x = $x_1$ 사이에서의 평균 변화율. 아래와 같이 정의

 => 두 점을 지나는 직선의 기울기

$\frac{\Delta y}{\Delta x} = \frac{f(x_1) - f(x_0)} {x_1 - x_0}$

미분 계수 differential coefficient

- 함수 y = f(x)가 주어질때, x = a에서의 미분계수는 다음과 같이 정의

$lim_{\Delta x -> 0}  \frac{f(a + \Delta) - f(a)} {\Delta x}$

- 위 비분계수가 수렴하는 경우 극한값은 f'(a)

 => x = a에서 미분 가능함.

미분 계수와 미소 증분

- 미소 증분 increment $\Delta x$: x가 0에 가깝지만 0이 아닌, 아주 작은 값의 증가.

- x = a에서 증분 값 $\Delta x$가 0에 가까워질때 평균 변화율은 순간 변화율이 되어 f'(a)로 표기

도함수 derivative

- 함수 y = f(x)가 주어질때, f(x)의 도함수를 아래와 같이 정의

f'(x) = $\frac{dy}{dx}$ = $\frac{df}{dx}$ = $lim_{\Delta x-> 0} \frac{f(x + \Deta x) - f(x)}{\Delta x}$

상미분 ordinary derivative

- 일변수 함수 y = f(x)에 대해, 함수 f를  독립 변수 x에 대한 도함수

- 도함수와 동일

f'(x) = $\frac{dy}{dx}$ = $\frac{df}{dx}$ = $lim_{\Delta x-> 0} \frac{f(x + \Deta x) - f(x)}{\Delta x}$

편미분 particial derivative

- 다변수 함수 y = f(x, y)가 주어질때, 함수 f에 대해 독립변수 x와 y 각각에 대한 도함수

$\frac{\sigma f}{\sigma x}$, $\frac{\sigma f}{\sigma y}$

접선의 방정식

- y = f(x)에서 x = a에서 미분 가능한 경우, 접선의 방정식

y = f'(a)(x - a) + f(a)

2. 미분 법칙 

함성 함수의 미분 - 연쇄법칙

- z = f(y),  y = g(x)가 주어질때 z를 x에 대해서 미분하면. 즉, z = f(g(x))의 x에 대한 미분

$\frac{dz}{dx}$ = $\frac{dz}{dy}$ $\frac{dy}{dx}$ = f'(g(x)) g'(x)

로피탈 정리

- f(0) = g(0) = 0이고, f'(0)과 g'(0)이 존재하면 아래의 식이 성립

$lim_{x->0} \frac{f(x)}{g(x)}$ = $lim_{x -> 0} \frac{f'(x)}{g'(x)}$

1. 수열

수열 sequence

- 자연수 N 집합을 정의역, 실수 전체 집합 R을 공역으로 하는 함수

 => f : N -> R

- 보통 수열은 a(n)으로 표기되어 f(n) = $a_n$이 됨

- 함수와 구별되도록 아래와 같이 표기

$a_1$, $a_2$, . . . = {$a_n$}

무한 수열 infinite sequence

- 정의역 N이 무한한 대응 관계를 갖는 함수

등차 수열

- 이웃하는 두 항의 차가 d로 일정한수열

$a_n$ = $a_1$ + (n-1)d

등비 수열

- 이웃하는 두 항의 비가 r인 수열

$a_n$= $a_1$ $r^{n-1}$

수렴 Convergence

- 수열 $a_n$에서 n이 증가함에 따라 $a_n$이 일정 값 $\alpha$에 가까워지는 현상

      => 수열 $a_n$은 $\alpha$에 수렴

- n이 무한대에 가까워질때 $a_n$이 $\alpha$로 수렴 하는것을 다음과 같이 표현

     => n -> $\inf$, $a_n$ -> $\alpha$ or lim$a_n$ = $\alpha$

발산 divergence

- 수열 $a_n$ 이 수렴하지 않는 경우

- 무한대로 갈수록 하나의 값에 가까워지지 않고, 매우 커지거나 매우 작아짐 

=>   n -> $\inf$ => $a_n$ -> $\inf$ or lim $a_n$ = $\inf$ {=$-\inf$}

진동 osillate

- 여러 값에 가까워지기는 하지만 한개의 값에 수렴하지는 않는 경우

 => 진동도 발산

수렴 수열과 경계

- 수렴하는 수열은 절대값이 유계(한계가 존재, bounded)

- 충분히 큰 실수 M이 존재하고, 모든 자연수에 대해 다음이 성립

|$a_n$| <= M

단조 증가 수열과 단조 감소 수열

- 단조 증가 monotone increasing : 수열 $a_n$이 아래의 조건을 만족하면서 계속 증가하는 경우

$a_n$ <= $a_{n+1}$

- 단조 감소 monotone decreasing : 수열 $a_n$이 아래의 조건을 만족하면서 계속 감소하는 경우

$a_n$ >= $a_{n+1}$

2. 급수

무한 급수 infinite series

- 무한 수열 $a_n$의 모든 항을 합한 식

$\sum_{k = 1}^{\infty}a_k$ = $\lim_{n -> \infty} \sum_{k = 1}^{n}a_k$

무한 등비 급수

- 일반 항이 $a_n$ = $a r^{n-1}$인 무한 등비수열의 급수

=> S = a + ar + a$r^2$ + . . . 

양항 수열과 양항 급수

- 양항 수열 : 모든 항 $a_n$이 0이상인 수열

- 양항 급수 : 양항 수열의 무한 급수

교대 급수

- 단조 감소하는 양항 수열 $a_n$이 존재할때, 교대 급수는 아래와 같다.

 $\sum_{n=1}^{\infty}$ $(-1)^{n-1} a_n$

- 위 교대 급수가 수렴하기위한 필요충분 조건은 아래와 같다.

$\lim_{n -> \infty}$ $a_n$ = 0

3. 함수의 극한

극한

- 함수 f(x)에서 x가 a로 가까워질때 f(x)가 상수 b로 가까워지는 현상

 => x가 a로 수렴할 때, f(x)는 b로 수렴함

- 이를 아래와 같이 표기

     1. $\lim_{x->a} f(x) = b$ 

     2. x -> a    =>    f(x) -> b

극한 값 존재 여부

- x가 a로 가까위질때, + 방향에서 가까워짐과 동시에 -방향에서도 가까워지는 값이 동일하면 극한 값이 존재한다고 한다.

  * 임의의 수 a에서 함수 f(x)가 끝어져, +방향과 -방향에 따라 f(x)서로 다른 값으로 수렴할수 있기 때문

$\lim_{x -> a^{-}} f(x) = b$ = $\lim_{x -> a^{+}} f(x)$ = $\lim_{x -> a} f(x)$ = b

4, 함수의 연속

함수의 연속

- 다음의 세 조건을 만족하면 f(x)는 x = a에서 연속함

 1. x = a에서 f(a)가 존재

 2. $\lim_{x -> a}$ f(x)도 존재

 3. $\lim_{x -> a}$ f(x) = f(a)

함수와 연속

- 함수 f(x)가 특정 구간에서 모든 점에 대해 연속일 떄 => f(x)는 그 구간에서 연속 continuous

- 모든 점에서 연속이지 않은 경우 => f(x)는 그 구간에서 불연속  discontinuous

최대 최소 값 정리 extreme value theorem

- 닫힌 구간 [a, b]에서 f(x)가 연속이면, 반드시 이 구간에서 최대 최소값을 가짐

 * 닫힌 구간 [a, b] : a ~ b사이 범위. a와 b 포함

 * 열린구간 (a, b) : a ~ b사이 범위이나 a와 b는 불포함

중간값 정리 intermediate value theorem

- 아래의 조건을 만족할 떄

 1. 닫힌 구간 [a, b]에서 f(x)가 연속

 2. f(a) < f(b)

- 중간값 정리 : f(c) = u인 c가 닫힌 구간 [a, b]에서 적어도 하나는 존재

EMC 관점 수동 소자

1. 저항

2. 캐패시터

3. 인덕터

4. Ferrite Bead

5. EMI Filter

6. Common Mode Choke Coil

7. 3단자 캐패시터

저항 registor

- 전류 흐름을 억제하는 소자

- 옴의 법칙 : I = V/R

- 저항 특성 : 캐패시터 , 인덕터와 달리 전력 소모

- 기호

- 물리적 원리 : rho는 물질의 비저항(고유저항), s는 물질의 단면적, l은 길이

           => 저항은 고유저항과 길이에 비례, 단면적에 반비례

저항의 종류

1. 직렬 접속 저항

- V = IR에 따라 R은 직렬합

2. 병렬 접속 저항

- 병렬 접속으로 인해 직렬에 비해 저항의 크기가 줄어듬

캐패시터 capacitor

- 에너지 저장하는 소자

- 저장 에너지

- 교류 저항

- 시간 영역에서 캐패시터의 전류 전압과의 관계식

- 기호

- 물리적 원리 : epsilon_0는 자유공간 유전율, epsilon_r은 비유전율, d는 전극간 거리, S는 전극 면적

캐패시터의 합성

1. 직렬 연결

2.병렬 연결

캐패시터와 SRF Self Resonant Frequency

- 동작 주파수가 증가할수록 Passive 소자의 제작 구조상 발생하는 기생 캐패시턴스와 인덕턴스의 영향으로 의도된 임피던스 특성과 겨양과 반대로 동작하기 시작하는 주파수

- 캐패시터의 경우 SRF보다 높은 주파수에서 인덕터로 동작

휴대폰 비행기 모드의 필요성

- 전자 시스템 전파 간섭 우려 때문에 필요

=> 전화, 메시지, 인터넷 등이 사용 불가

- 비행기 운형에 영향을 주는 전자파

=> 항공기 운행 오작동 발생 가능

전자파란?

- 주기적으로 세기가 변하는 전자기장이 공간속으로 전파해 나가는 파동 현상

- 아래의 그림은 전자파를 이루는 전기장과 자기장을 보여줌

전자파의 반사, 굴절, 회절

- 반사 : 입사한 전자파가 되돌아가는 현상

- 굴절 : 산란체의 경계면에서 전자파 진행경로가 꺾이는 현상

- 회절 : 장애물에 의해 전자파가 도달할수 없는 곳에서 전자파가 전파되는 현상

 * 방송이나 무선통신에서 송신 안테나를 볼수없는데도 전자파를 수신함

전자파의 세기

- 전자파 발생원으로부터 거리에 따라 급격히 감소

- 자유 공간 진행(직접파)하거나 반사 또는 굴절된 전자파의 전력은 거리의 제곱에 반비례하여 감소

- 회절된 전자파의 전력은 거리에 반비례하여 감소

 * 회절된 전자파는 회절이 일어나는 지점에서 세기가 크게 줄어들므로 직접파나 반사파, 굴절파에 비해 세기가 크게 약해짐

주파수 스펙트럼과 용도

- 아래의 그림은 각 주파수대역별 용도를 보여줌

전자파 관련 용어

EMC(Electro Magnetic Compatibility)

- 전자파 적합성or 전자파 양립성

- 기기외부로 불요 전자파를 최소로 방출시켜 다른 기기에 전자파 간섭을 일으키지 않고, 외부로부터 전자파 간섭에 영향을 받아도 정상적으로 동작할 수 있는 상태

EMI - Electro Magnetic Interference

- 전자파 간섭

- 전류 흐름에 의해 도선에 자연적으로 발생되는 에너지가 타 기기에 방해 간섭원천으로 동작되는 형태

EMS Electro Magnetic Susceptibility

- 전자파 내성

- 외부의 전자파 간섭으로부터 전자기기가 간섭을 받음에도 얼마나 기능을 하는가 의미

EMI 전자파 간섭의 종류

- RE Radiated Emission 방사방출 : 30MHz 이상 회로서 발생. 전자파가 공기로 방사되는 전자파를 잡음

- Conducted Emission 전도 방출 : 30MHz 이하 회로에서 발생. 신호선, 전원선 같은 매질로 전달되는 전자파 잡음

-ESD ElectroStatic Discharge 정전기 방전

   : 서로 다른 정전기 전위 가진 물체가 가까워질때 갑작스러운 전하 이동으로 과전류 흘러 오작동 발생하는 현상

- RS Radiated Susceptibility 방사 내성 : 자유공간으로부터 전파되어오는 전자파 간섭에 견디는 정도

- CS conducted Susceptibility 전도 내성 :외부 케이블, power cords, IO interconnect 등에서 오는 전자파 간섭에 견디는 정도

- EFT/Burst Electrical Fast Transient/Burst : 전기적 빠른 과도 현상

- Surge : 전기회로에서 수초간 지속되는 전압, 전류, 전력의 과도 현상

- Voltage Dip : 전압 강하. 전압 감소 전자 시스템의 한 지점에서 전압이 급격히 감소했다가 짧은 시간 후에 회복되는 현상

- hazard 위해 : 전자파가 유기체에 미치는 위협

- EMP Electro Magnetic Pulse : 전자파 펄스. 

전자파 발생 원리

- 아래의 그림은 전자기파의 발생 원리를 보여줌

- 전선을 따라 전류가 흐르면 주위에 전기장과 자기장이 형성됨

- 아래의 그림은 LC회로로. 축전기와 코일이 규칙적으로 진동하는 회로

전파의 속도

- 지구 7바퀴 반 도는데 1초

- 지구에서 화성가는데 3.3초

- 지구에서 태양가는데 8분 3초

- 전파의 속도 초당 30만 km

전자파 환경

- 자연 잡음 :자연적 현상에 의해 발생하는 잡음

       => 대기 잡음 : 번개, 이온층 임펄스, 슈만공진

      => 우주 잡음 : 태양 흑점 활동, 천체 축 열 잡음

- 인공 잡음 : 인간이 사용하는 기계에 의해 발생하는 잡음

    => 의도적 잡음 : 제품 성능 및 기기 동작을 위해 고의적으로 Rf에너지 발생시키는 경우

        * 예시 : 송신기 고조파, 수신기의 국부발진기(AM/FM), TV의 동기 펄스, 마이크로프로세스

    => 비의도적 잡음 : 제품의 성능 또는 기능 동작을 수행하는 동안 비의도적으로 RF 에너지가 발생

       * 예시 : 전동기, 전기접점 기기(릴레이, 스위치), 스파크 방전(이그니션), 코로나 방전(송전선)

전자파 기술 변화 과정

1. 1900년대 이전 - 전자파 개념 존재 x

- 교환 시설 : 수동식(자석식/ 공전식)

- 전송/정보/이동통신 : 기술 발전 미흡

- 전자파 환경 : 자연환경에 의한 전자파가 존재

2. 1900년대 - 전자파 활용 기술 연구

- 교환시설 : 기계식 (STM/EM/Cross-Bar)

- 전송 : 아날로그 전송기술 사용(나선 반송/동축케이블/PCM방식)

- 전자파 환경 : 군사 목적에 의해 중요성 인식 시작

3. 1970년대 - 군사 목적에 의한 전자파 대응

- 교환시설 : 반전자식 교환기 (No.1AESS)

- 전송 : 아날로그 방식 이동전화 상용화

- 전자파 환경 : 무선 분야 기술 전개에 따른 전자파 중요성 인식

4. 1980년대 - 선진국 중심 EMI 자율적 규제

- 교환시설 : 전전자식

- 이동통신 : 아날로그방식 세계적 운영

- 전송기술 :광통신망 이용

- 전자파 환경 :전자 산업 발달에 따른 전자파 문제 발생 및 중요성 강조

   => 전자파 규제 시작

5. 1990년대 - 국내 산업기기 EMI 승인 의무화

- 디지털 시대

- 전파환경의 복잡, 무선 시설이ㅡ 발달

- 사용 주파수 대영 증가

- 전자파 환경 : 전자파 세계적 강제 규제

    =>세계 각국 자국 산업 보호를 위한 규제

6. 2000년대 - 전자파 규제 범위 확대

- 유무선 위성통신의 통합

- 첨단 멀티미디어 시대 IMT-2000

- 전자파 환경 : 소비자 및 제품 품질 수준의 척도. => EMI규제에서 EMS 분야로 확대

EMC 문제 대두 배경

1. 전기 전자기기의 디지털화

- 아날로그 회로 : 잡음의 영향이 일과성이 강함

- 디지털 회로 : 메모리 소자 내장, 낮은 직류 전류에서 동작 => 미약한 잡음 영향이 메모리에 기억되어 오작동 발생

2. 전기 전자기기의 저전력화

 - 기기의 소형화,  전지의 긴 수명 확보

   => 동작 전압이 낮아짐(저전력화) => 같은 잡음 레벨에도 장애 발생

3. 전기 전자기기의 고밀도화

 - CPU가 내장된 디지털 기기의 급속한 보급

 => 좁은 공간에 인접해짐 => 각기기간 전자파 간섭이 심해짐

목표

- 전기전자기기 설계시 전자파 적합성 전반을 이해도를 높여 초기 설계 단계에서 대책을 수립

- 회로에 반영하여 EMC 문제로 인한 비용을 최소화 하기 위함

OrCAD ( CAD : Computer Aided Design)

- cad : 컴퓨터 기반 설계의 약어

- 제도가 아닌 컴퓨터를 이용한 설계

- 전자 분야에서 설계 자동화에 사용되는 프로그램을 EDA( Electronic Design Automation, 전자설계 자동화) 라고 부름

CAD 프로그램 종류

- PADS, P-CAD, CADSTAR

- OrCAD : 전자회로설계, 회로시뮬레이션, 회로기판 설계

OrCAD

- EDA 전자 설계 자동화 프로그램중 하나로 국내에서 보편적으로 사용됨

- 주요 프로그램

OrCAD Capture 특징

- 회로도 Schematic 분석을 쉽게 도와줌

- 전자회로 도면을 그려서 이를 인쇄회로기판 PCB : Printed Circuit Board로 구현하기 위한 Netlist File을 생성 가능

- 명령어의 빠른 접근을 위한 툴바와 툴 팔레트 제공

- 부품 목록, 도면 정보등을 문서화 시켜서 이를 데이터베이스화

- Excel, Lotus 등 각종 스프레드 시트 등과 파일 호환 가능

회로도 작성 방법

1. 프로젝트 시작

2. 설계 환경 설정

3. 부품 배치 및 배선하기 ( 부품 생성, 라이브러리 추가, 풋 프린트값 입력)

4. 어노테이트 (참조값 갱신)

5. DRC ( Design Rule Check)

6. 후처리 파일(네트리스트, BOM 파일 등) 생성