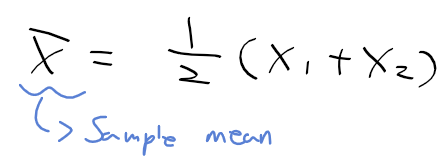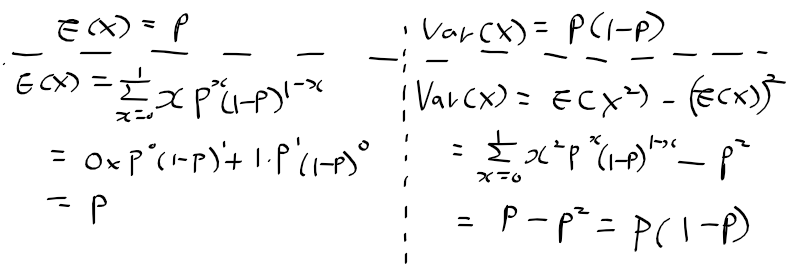집밖은 위험해

오늘날 사용되는 다양한 제어 이론들

- 고전 제어

- 현대 제어

- 강인 제어

자동 제어

- 공학 및 과학에서의 핵심 분야 중 하나

- 우주선 시스템, 로봇 시스템, 제조 시스템 등 다양한 산업 전반에서 사용

제어 이론의 역사

- 18세기 : 제임스 와트의 증기기관을 이용한 속도 제어

- 1922 : minorsky는 자동화 제어기 분야 연구. 시스템에 대한 미분 방정식으로 배의 안정성 유지되도록 구함

- 1932 : 나이퀴스트가 정현파 입력에 대한 개루프 시스템의 정상상태 응답으로 폐루프에서 안정성을 구하는 과정 설계

- 1940

    1. 보드 선도를 이용한 주파수 응답을 활용하여 성능 요구를 만족하는 선형 폐루프 제어기를 설계할수 있게됨.

    2. 압력, 온도등 제어하기 위한 PID 제어기가 산업 전반에서 사용됨

    3. 지글러와 니콜이 PID 제어기 튜닝 방법을 소개.

    4. 에반스가 루트 로커스 방법을 제안

- 1960 

   1. 디지털 컴퓨터가 만들어지면서 복잡한 시스템에 대한 시간 영역에서의 해석이 가능해짐.

   2. 현대에 들어와 복잡해진 제어기와 정밀도가 요구되는 일들을 다루기위함.

- 1960 ~ 1980

    1. 결정론적이고, 확률적인 시스템에 최적으로 제어하고, 복잡한 시스템에 적응해나가는 방법들이 연구됨

- 1980 ~ 1990

    1. 강인 제어에 대한 연구가 이루어짐.

고전 제어

- 주파수 응답과 루트로커스 방법은 고전 제어 이론의 핵심이되어 여러 성능 요구사항들을 지킬수 있었음.

- 하지만 고전 제어 이론은 단일 입력, 단일 출력 시스템에서만 사용가능

- 다중 입력, 다중 출력 시스템에서는 사용 불가

현대 제어

- 시스템 미분방정식의 시간 영역에 대한 해석을 기반

- 현실에 존재하는 제어 시스템을 수학적 모델링 하여 활용

-실제 시스템과 모델 사이의 오차가 존재하며, 이 오차에 시스템 안정성이 영향을 받음

1. 제어 시스템 소개

2. 시스템 수학적 모델링

3. 상태 변수 모델

4. 궤환 제어 시스템 특성

5. 피드백 제어 시스템 성능

6. 선형 피드백 시스템의 안전성

7. 루트 로커스 방법

8. 주파수 응답 방법

9. 주파수 영역에서의 안정성

10. 피드백 제어기 설계

11. 상태 변수 피드백 시스템 설계

12. 강인한 제어 시스템

13. 디지털 제어 시스템

1. 제어시스템 소개

 1.1 소개

 1.2 자동화 제어에 대한 역사

 1.3 제어 시스템의 예시

 1.4 엔지니어링 설계

 1.5 제어 시스템 설계

 1.6 기계적 시스템

2. 시스템 수학적 모델

 2.1 소개

 2.2 물리적 시스템에대한 미분 방정식

 2.3 물리적 시스템을 선형 근사화 하기

 2.4 라플라스 변환

 2.5 선형 시스템 전달함수

 2.6 블록 다이어그램

 2.7 signal flow 그래프 모델

 2.8 디자인 예시

 2.9 제어 설계 프로그램을 이용한 시스템 시뮬레이션

3. 상태 변수 모델

 3.1 소개

 3.2 동적 시스템의 상태 변수

 3.3 상태 미분 방정식

 3.4 signal-flow 그래프와 블록 다이어그램 모델

 3.5 signal flow 그래프와 블록 다이어그램을 대신할 방법들

 3.6 상태 방정식을 전달 함수로 변환하기

 3.7 시응답과 상태 전이 행렬

 3.8 디자인 예시

 3.9 제어기 설계 소프트웨어를 사용한 상태 변수 모델 해석

4. 피드백 제어 시스템 특성

 4.1 소개

 4.2 에러 신호 해석

 4.3 파라미터 변동에 따른 제어 시스템의 민감도

 4.4 피드백 제어 시스템에서 요란  신호

 4.5 제어기 과도 응답

 4.6 정상 상태 응답

 4.7 피드백 비용

-- 생략---

반도체 semi(반) conductor(도체)

- 도체 : 전기가 잘통합

- 절연체 : 전기가 잘 안통함

- 도체와 절연체의 중간

- 열, 빛, 자장 등 영향으로 성질이 크게 바뀌어 다양한 용도로 사용 가능

=> 방송, 통신 기기, 가전, 로봇 등 모든 전기전자기기에 사용 

=> IT산업의 쌀

반도체의 주원료

- 초기 : 게르마늄

- 오늘날 : 실리콘

윌리엄 브래드포드 쇼클리와 반도체

- 전자는 반도체라는 고체 안에 존재

반도체란

1. 원자구조

2. 반도체와 공유결합

3. 진성 반도체와 불순물 반도체

원자의 정의

- 물질의 특성을 갖는 더이상 쪼갤수없는 작은 입자

- 특정수의 전자와 양자 가짐

보어의 원자 모델

- 원자 핵(nucleus)과 전자(electron)으로 구성

- 원자핵은 양성자 potron, 중성자 neutron으로 이루어짐

- 전자는 음-으로 대전된 입자

원자번호와 질량

- 원자번호 tomic number : 전기적 중성인 원자속 전자의 수

- 주기유표 periodic table : 원자 번호와 질량 순으로 배열

- 중성상태 neutral : 모든 원소의 원자는 양자의 수와 동일한 전자 개수를 가짐 => 전기적 중성

전자각 shell

- 원자 내 전자는 핵으로부터 일정한 거리 궤도를 그리며 움직임

- 전자가 돌고있는 궤도.

- 개발적인 전자각은 허용된 에너지 준위에서 한정된 수의 최대 전자를 가짐

- 최외각, 가전자각 : 가장 바깥쪽의 궤도

- 가전자 valence : 최외각 전자를 돌고있는 전자. 더 높은 에너지 준위를 가지는 전자. 핵으로부터 인력이 최소.

           => 화학적 반응, 물질의 구조, 전기적 성질 등에 영향을 미침

이온화

- 원자가 열 혹은 빛 에너지흡수

- 핵으로부터 이탈(자유전자)  중성 -> +를띄는 양이온

- 새 전자가 원자궤도로 들어오면. 중성 -> 음이온

반도체와 공유결합

반도체란?

- 전기가 잘통하는 도체와 통하지 않는 절연체의 중간적 성질을 나타냄

- 순수한 상태에서 부도체와 비슷한 특성

- 불순물 첨가에 의해 전기전도도가 늘어나고, 빛이나 열에너지에 의해 일시적으로 전기전도성을 갖는 물질

- 도체 절연체의 차이를 어떻게 알까 -> 구분은 해당 물체의 에너지 대역의 차이로 알 수 있음

실리콘 Si의 에너지 대역

가전자대

- 전자들이 가질수 있는 가장 높은 에너지 준위

- 원자핵의 영향을 아직 받고 있는 에너지준위

-> 외부 에너지에 의해 핵의 구속을 벗어날 수 있는 에너지 준위

전도대

 - 가전자대의 전자가 원자핵의 구속으로부터 이탈하여 이탈하여 자유로워지는데 필요한 에너지 준위

-> 자유 전자가 존재

절연체, 도체, 반도체 비교

- 절연체 : 에너지간격이 매우큼. 높은 에너지저항. 가전자대에서 전도대로 전자이동이 힘듬(고무, 나무)

- 도체 : 에너지간격이 거의없음. 전도대에 많은 자유전자가 존재. 매우 낮은 에너지저항(구리, 금, 은)

- 반도체 : 에너지간격이 절연체보다 작고 도체보다 큼. 외부 에너지가 없으면 절연체와 같음. 얻으면 전류흐름

실리콘 원자결합

- 4개의 원자로 구성됨

- 진성 반도체 : 불순물이 섞이지 않은 순수 반도체

 * 옥텟 규칙 : 가전자가 8개일때 가장 안정한 상태가 됨

공유 결합

- 4개의 가전자를 가지는 실리콘 원자는 주위 다른 4개의 실리콘 원자와 가전자 공유하여 결합

- 실질적으로 8개 가전자로 구성되어 화학적으로 안정되게 하는 결합

반도체에서 어떻게 전류가 흐를까

자유 전자와 정공

- 자유 전자 : 빛, 열 에너지를 얻으면 가전자 에너지가 커져 궤도를 이탈해 자유전자가 됨

- 정공 hole  : 자유전자로 궤도를 이탈하고 남은 빈자리

- 재결합 recombination : 궤도를 이탈한 자유전자가 에너지를 읽고, 가전자대의 빈자리로 다시 돌아오는 현상

자유 전자들의 이동 - 전자 젼류 electron current

- 자유전자와 정공은 반도체에 전류를 흐르게하는 반송자

1. 실리콘 양끝에 전압 인가

2. 자유전자들은 전계에 의해 쉽게 +로 이동

3. 전류가 생성

정공 전류 hole current 생성

- 정공이있는 가전자 레벨에서 발생

- 약간의 에너지를 얻으면 근처의 정공으로 이동 -> 다른 빈자리를 생성

공유 결합 방법에 따른 반도체의 분류

- 진성 반도체

- 불순물 반도체 : p형 반도체, n형 반도체

진성 반도체

- 4가 반도체 원자 이외에 다른 원자(불순물)이 없는 상태

- 안전한 공유결합으로 외부 에너지를 얻어도 전도대가 존재하는 자유전자와 가전자대에 존재하는 정공이적음

   => 전도도가 낮다

불순물 반도체

- 전도도를 높이기 위해 불순물을 섞어 전자나 정공의 수를 늘린 반도체

- 도핑 doping : 순수 반도체에 불순물을 넣어 반송자(전기를 전도하는 전자와 정공)를 증가시키는 과정

- 정공을 증가시킨 P형 반도체와 자유전자를 증가시킨 N형 반도체가 존재

P형 반도체

- 정공 수를 늘리기 위해 3가 불순물 원자(알루미늄, 붕소) 첨가

- 4가 원자에 3가 원자를 첨가하면, 공유 결합으로 8개 최외각 전자가 필요하나 1개의 빈자리(정공) 생성

- 다수 반송자 majority carrier : 정공

- 소수 반송자 minority carrier : 전자

N형 반도체

- 자유 전자를 늘리기 위해 5가 불순물 원자(비소, 안티몬) 추가

- 4가 원자에 5가 원자를 첨가하여 공유 결합으로 8개 가전자가 사용되나 1개의 여분의 전자(자유전자) 생성

- 다수 반송자 : 전자

- 소수 반송자 : 정공

모집단 population

- 관심의 대상 전체

표본 sample

- 모집단의 일부분

모수 parameeter

- 모집단은 특정 분포를 따름

- 모집단의 특성을 나타내는 값(모집단이 변경되지 않는 이상 상수)

통계값

- 표본으로부터 얻은 값

 * ex. 임의로 선정한 1000가구의 평균 지출이 100만원인 => 100만원이 통계값

통계량 statistic

- 통계 값을 구하기 위한 수식

- 대표적인 통계량으로 표본 평균

표본 평균 구하기

- 확률 변수 X1, ..., Xn가 평균 mu, 분산 sigma^2인 모집단에서 추출된 경우

- 모집단의 평균 mu를 추정 inference 하기위한 표본 평균은 아래와 같음

주사위에 대한 확률 분포와 모수 구하기

- 주사위는 1 ~ 6까지 확률 변수값을 가지는 이산 균일 확률 분포를 따름

 => 모집단의 평균과 분산은 다음과 같이 구함

표본 크기가 2인 경우 주사위 표본 평균 구하기

- 이번에는 확률 변수 X1, X2가 주어질때 표본 평균을 구하면 다음과 같이 정의함

- X1과 X2가 아래와 같이 주어질때 표본 평균 bar{X}는 아래와 같다.

표본의 크기가 2인 표본 평균의 확률분포표

- 주사위를 두번 던질때 얻을수 있는(X1, X2의 조합) 표본 평균에 대한 확률 분포표는 아래와 같다.

표본의 크기가 2인 표본의 통계값

- 위 표본 평균에 대한 확률 분포가 주어질때 기대값과 분산은 아래와 같다.

=> 모 평균과 표본 평균은 7/2로 동일하나 표본 분산은 모 분산의 1/2가 됨.

표본 크기가 n인 표본 평균 bar{X}의 기댓값과 평균

- 다음과 같이 n개의 표본들이 주어질 때

- 이들을 샘플링하여 뽑은경우 표본 평균 bar{X}의 기댓값과 평균은 아래와 같다.

 => 1. 모 평균과 표본 평균은 동일

      2. 표본 분산은 모 분산/n

대수의 법칙

- 표분의 수가 커지면 표본 평균 bar{X}는 모 평균 mu에 수렴

모집단이 정규분포일때 표본 평균 분포

- 표본 평균은 모집단을 추정하는데 사용되므로 매우 중요

- 모집단이 정규 분포를 따르면 -> 표본 평균도 정규 분포를 따름

중심 극한 정리 central limit theorem

- 모집단이 정규 분포가 아니어도 표본 n이 충분히 크면 표본 평균은 정규 분포에 근사

자료 분석의 주요 관심사

- 두 변수 사이의 관련성

 * ex. 광고비와 순익의 연관성

결합 분포 joint distribution

- 2개 이상의 확률 변수들을 같이 고려한 확률 분포

 * ex. 키에 대한 확률 변수 X와 몸무게에 대한 확률 변수 Y => 키가 180cm 이상이고, 몸무게가 80kg 이상일 확률

다변량 확률 분포 multivariate distriubiton

- 여러 확률 변수들의 결합분포

이변량 확률 분포 bivariate distribution

- 두 확률 변수의 결합 분포

결합 확률 분포의 기대값, 공분산, 상관계수

1. 기댓값 expectation

- 이산/연속 확률 변수가 주어질때 결합확률질량/밀도 함수에 대한 기댓값은 아래와 같다.

2. 공분산 covariance

- 두 변수간의 관계를 나타내는값

3. 상관 관계 correlation

- 공분산은 각 확률 변수의 단위에 의해 정해짐

 => 각 변수의 표준편차를 나누어 표준화한 상관계수(rho)로 상관관계를 알 수있음

- 아래는 상관 계수의 식

조건부 확률 분포 conditional probabilistic distribution

- 조건부 분포 : 두 확률 변수 (X, Y) 중 Y의 값이 주어질때 X의 확률 분포

 * ex. X는 키, Y는 몸무게라고 할때, 몸무게가 80인 경우 키에 대한 확률 분포

- 두 확률 변수 X, Y가 주어질때 조건부 확률 분포는 다음과 같이 정의 가능

이변량 정규분포 bivariate normal distribution

- 정규분포를 2개의 변수에 대해 결합 분포로 확장한 것

 * ex. 키와 몸무게에 대한 확률 변수를 이변량 정규분포로 표현 가능

- 다음의 경우 두 확률 변수 X1과 X2에 대한 이변량 정규분포를 정리함

다변량 정규분포 multivariate normal distribution

- 이변량 정규분포와 마찬가지로 벡터와 행렬로 간편하게 표현 가능함

- p개의 확률 변수 X1, ..., Xp가 다변량 정규분포를 따르는경우 X1, .., Xp의 결합 확률 밀도함수는 다음과같음

 * 행렬식 determinant : 행렬의 역행렬이 존재하는지 판별하는 식

- 확률 변수 X가 다변량 정규분포를 따를때 다음과 같이 정리할 수 있다.

연속 확률 분포 continuous probability distribution

- 확률 변수가 연속(셀수 없는)인 경우에 대한 확률 분포

- 예시 : 균등 분포, 지수분포, 정규분포 등

연속 균등(균일) 분포 continuous uniform distribution

- 구간 [a, b]에 균일하게 분포된 확률 분포

- 균일 분포의 확률 밀도 함수와 표기를 다음과 같이 한다.

지수 분포 exponential distribution

- 사건이 독립일때, 일정 시간 동안 발생한 횟수가 포아송 분포를 따른다면, 다음 사건 발생까지 대기시간은 지수 분포를 따름

- 제품 수명에 대한 확률 분포로 자주 사용

  ex) 평균 수명이 1000시간인 부품이 있을때, 1000시간 이전에 고장날 확률은?

- 지수 분포의 확률 밀도 함수

- 지수 분포 예시 그림

정규 분포 normal distribution

- 평균점을 중심으로 좌우 대칭이며 종 모양의 확률 분포. 널리 사용됨

- 에시 : 학생들의 성적 분포, 남성의 콜레스테롤 수치 분포 등

- 정규분포는 다음과 같이 확률 밀도 함수와 표기를 한다.

- 정규 분포의 확률 밀도 함수

이산 확률 분포 discrite probability distribution

- 주사위 눈의 값과같이 (셀수 있는) 이산적인 확률 변수를 갖는 확률 분포

이산 균등 분포 discrete uniform distribution

- 모든 확률변수에서의 확률 값이 동일(균일)한 확률 분포

초기하 분포 hypergeometry distribution

- 표본 조사시 모집단에서 표본을 비복원 추출을 하는 경우 이용됨

베르누이 분포 bernoulli distribution

- 베르누이 시행 : 서로 배반인 두가지 경우만 발생하는 사건

    ex. 동전 앞면/뒷면,  양품/불량품

- 베르누이 시행 확률 질량 함수

- 기대값과 분산

이항 분포 binomial distribution

- 일정 확률 p를 가진 독립시행을 n번 반복했을때의 확률 분포

- 이항분포의 확률 질량 함수 pmf와 이에 대한 표기를 다음과 같이 한다.

포아송 분포

- 발생 가능성 p는 매우 작지만 시행횟수 n은 충분히 큰 경우 사용하는 분포

- 포아송 분포는 이항 분포의 근사라 할 수 있음

- 포아송 분포의 확률 질량 함수와 포아송 분포를 따르는 확률 변수 X에 대한 표기

- 아래의 그림에선 시행횟수는 k, 발생 게인은 lambda 

처음 라이노 연습하면서 간단한 사각형 모델 만들기 까지 진행했다

오늘 배운 것들과 함수들

1. 점 연습

2. 선 긋기 (폴리 라인)

3. 곡선그리기 - 제어점 커브와 커브 보간점( shift를 눌럿더니 대각선으로 가지더라)

4. 원 그리기

5. 호 그리기

6. 커브 필릿 – 연결된 두 직선사이 곡선, 떨어진 두 선 사이 곡선을 부드럽게, 비슷한걸로 각지게 만드는 기능도

7. 트림 – 삐져나온 선 지우기

8. 조인, 분해 – 단일 요소들을 합치고 나누기

9. 서피스 – 점, 선 요소로 평면 만들기

10. 상자 높이기, 원뿔 만들기

11. 로프트 – 중심 선들을 뒤덮는 입체

12. 선형치수 – 기하학적요소들의 길이 재기

13. extrudecrv – 선 돌출시키기 -> 3차원화

14. filetedge – 가장자리(모서리) 다듬기

15. blendcrv – 떨어진 두 선 사이 곡선 넣기.

* 트림으로 이어진 곡선을 떨어트린후 넘어간 부분들을 자름

-중략 -

16. filetedge - 가장자리 다듬기

17. sweep2 – 윗 면에서 아래 면을 감싸는 곡면 생성

18. split – 선 요소를 특점 점을 기준으로 나눔

=> sweep2에서 선 범위 지정에 활용

19. mirror – 기존의 요소를 거울에 비치듯이 복제

20. 결과물 – 탄젠트 커브의 경우와 이를 고친후 미러한 결과물

아두이노로 만들수 있는 프로젝트 들은 참많다

어떻게 만드는지 등은 다 아두이노 공식 홈페이지 상에서도 제공하고 있지만

막상 그런 제품을 만들 비용과 시간, 게으름 때문에 제대로 해볼 생각은 한적이 없었다.

다행이 이번에 하드웨어와 소프트웨어를 통합한 프로토타이핑을 하면서

이제서야 한번 시도해볼 기회가 생긴것 같다.

처음에는 원래 역 도립진자를 한번 만들어보고 싶었다.

본인은 제어 공학을 공부했지만 이론적인 내용과 간단한 메트랩 실습만 조금해보았지

실제 제어기 적인 내용은 제대로 만들어보지를 못했다.

그러다보니 이런걸 다루어보고싶었지만

하드웨어를 만들줄 모르니 엄두가 안나더라

그렇게 해서 제어기와 프로토타이핑을 결합한

역 도립진자를 생각하게 되었다.

이것 자체가 석사 논문에 쓰기도 하는 내용이기도 하고

적당한 거라 생각하려했는데

* 하다 하다 삼단 역 도립진자도 있다..

아두이노 예제 코드만 몇번 놀리고 말았던 내가 하기에는 조금 힘들것 같더라

대신 이전에 조금더 간단한 예제가 생각난게

초음파 밸런서가 있었다.

시소 처럼 생긴 구조물 끝에 초음파 센서와 공을 놓고

공이 너무 가까워지면 시소를 기울려 떨어지게 하고

너무 멀어지면 초음파쪽으로 기울어지도록 제어하는 예제였는데

이런식으로

한번 PID 게인들 조절하면서 찾아가는 과정을 한번 해보고 싶다.

처음부터 역도립진자하는것보단 쉽겠지

내가 배운 제어공학을 생각하면

분명 많은 시간을 들여서 신호와 시스템, 제어공학을 공부했지만

아직도 PID 제어기가 뭔지, 해가 뭔지 잘 정리되는 느낌이 들질 않는다.

아마 간단한 메트랩 예제만 해보고 말았지

실제로 제대로 된 프로젝트를 해본적이 없어서 그런것 같다.

이번 기회에 PID 제어기가 들어간 이러한 프로젝트를 직접 만들어 보고 싶다.

만약 정말 시간이 남는다면

조금 더 어려운 프로젝트로

아두이노 강아지나 자율주행 차량용 차체 같은것을 만들어 보고자 한다.

이전에 자율주행 차 연구를 할때

하드웨어에 대해서 아는게 하나도 없어

장난감 자동차에다가 수백만워너치 장비들을 올려서 사용하곤 했었다.

보기도 너무 안좋고 심하게 조잡했다.

다른 곳에서 로봇 만든다고하면

이런 장난감 차체가아니라 실제 기구 제작해서 만든다는데

이런것 밖에 쓸수없는게 너무 자존심 상하더라

이런거 만들어보고싶다..

개인 프로토타이핑 목표

1. 초음파 기울기 

2. 역도립진자 만들기

제품 디자인 프로세스

1.  디자인 방향 설정

2. 디자인 컨셉 설정

3. 스케치 1차 시각화

4. 스펙 및 개발 레이아웃 설정

5. 3d 디자인 모델링

6. 3d 렌더링 등 2차 시각화

7. 프로토 타입 등 실물 확인 작업

8. 개발 실장 검토

9. 디자인 및 개발 개선

10. 디자인 목업, 워킹 목업 제작

------------ 목표------------

11. 금형 검토 및 양산성 검토

12. 금형 제작 및 시사출 검토

    * 시사출 검토 : 전문가들이 금형을 만들어도 안되는 경우가 많음. 문제 검출 

13. CMF 시방서 및 샘플 제작

14. 품질 감리 및 양산

제품 디자인 프로세스에 관한 이야기

규모에 따라 와따가따가 건너띄기도

=> 적립이 안되고, 비용을 줄이기위함

-> 그렇다고 안되는건 아님 (목적에 부합하는것이 가장 중요, 이게 합리적일수도)

금형이란?

- 틀을 의미

드라프트?

- 사출물이 빠져나올수있는 각도를 줄임 정밀하느냐에 따라서  달라질 수있음 어떤 

=> 3d 프린팅에는 그런게 없기 때문. 어떤 형상에서든 제한이 존재하지 않음

디자이너 정의의 필요성

- 많은 사람들이 비전은 있지만 명확하지 않음

- 디자이너가 풀어줌

=> 깔금하게 만들어주세요라는 경우가 많음

- 스코프 정의 가 중요

일의 범위(스코프) 정의 

- 비용, 시간, 일정이 일의 범위에 따라 정해지기때문

- 비지니스  환경과 스코프 설정 이해 필요

대기업과 디자인

- 어느정도 설정이 정리되서 온다

- 디자이너들은 이 제품이 동작과 기능 어떻게 심미적으로 아름답게 보이는지 신경을 많이 쓰임

    => 컨셉 설정의 많은 부분 차지

- 디자인 리서치 팀도 따로있음 

    => 체계화가 되있으나 경험의 폭이 좁음

- 학생들이랑 비슷 판넬에다 아이디어 키워드 붙이고 정리

스케치와 시각화

- 바로 3d도 문제될수 있으

- 스케치, 모델링 다 과정

- 3d로 해봐야디겟느넫 3d해보고 유기적으로 와다가다가 중요

- 스케치 멋잇게 해봣자 결과 안나오면 otl

- 스캐치 상에서 개발 관련된 얘기는 잘하지 않음. 그러다 잘못되는 경우가 많음

 => 스타트업이 의사결정이 빠르다 ...

레이아웃

- 완성된 제품을 봤을때. 산출물 껍데기를 뺀 상태를 레이아웃

- 레이아웃이 있어야 겉데기를 만들수 이따

- 레이아웃이 와따가따하다가 3d 디자인 검토

랜더링

- 키샷 같은 프로그램으로 얘기해보면 좋을듯

- 제대로된 후가공은 힘들듯

개발 실장 검토

- 개발이 가능한지 여부를 다룸

디자인 프로세스 필요 역량

- 다음 기술을 기반으로 캐드와 프로토타이핑 와따가따

- 비슷하진 않더라도 거슬리지 않게 하기도 힘듬

디자인 프로세스 장비

1. 3d cad(라이노)

 - 3d 형상 제작 및 데이터화

 - 컨셉 정리

2. 3D 프린터

 - 프로토타입, 부품, 양산 등에 활용 가능

 - 퀄리티에서 변수 존재

3. 레이저 커터

 - 2d 작업에 적합(판을 자르는ㄷ ㅔ 사용)

 - 2d 이상 작업 힘듬. 열로 인한 마감 문제 발생

3D CAD 개념

1. 폴리곤 모델링

- 유기체에 적합

- 다양하고 자유로운 표현 가능

- 수취화 힘듬

2. Nurbs 모델링

- 고정 물체에 적합

- 정량적이고 수치화에 용이함

- 자유로운 표현이 힘듬

프로토타입 목표 - 구체화 ver.1

1. 가장 간단한 프로젝트 

 - 초음파 발란서

2. 중간 난이도 프로젝트

 - 역 도립진자

3. 고 난이도 프로젝트

 - 중형 자율차 차체

4. 초고난이도 프로젝트

 - 개 로봇