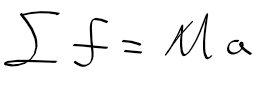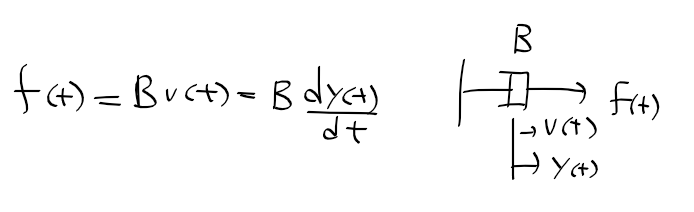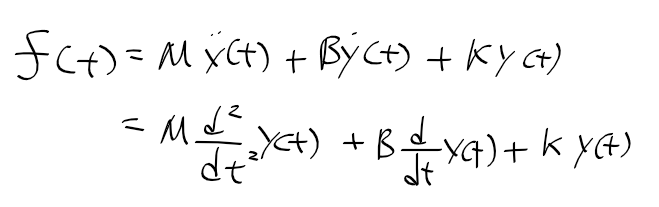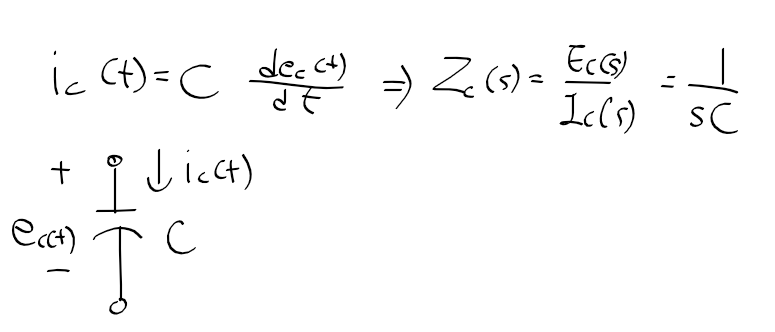집밖은 위험해

회전 운동 rotation

- 고정된 축을 중심으로 회전하는 운동

회전 운동에서의 뉴턴의 운동 방정식

- 힘 대신 토르크 torque T

- 질량 대신 관성 inertia J

- 가속도 대신 각가속도 alpha

=> 회전 운동에 작용하는 모든 토르크의 합 = 관성 * 각가속도

- 각가속도 alpha는 각속도 omega와 각변위 theta와 다음과 같은 관계를 가짐

관성 inertia

- 회전 운동의 운동 에너지를 저장하는 요소

토크 관성 시스템과 운동 방정식

- 관성이 J인 물체에 토크 T(t) [N m]이 가해질때 운동방정식

비틀림 스프링

- 비틀림 스프링은 토크에 비례하여 각변위가 생김

마찰

- 회전 운동에서 댐핑 마찰은 마찰 계수 D를 사용하여 다음과 같이 표현

회전 운동에서의 질량-스프링-댐핑 시스템

- 아래의 같은 회전 운동하는 원판이 주어질때, 우측과 같은 작용 반작용이 발생

- 이에 대한 운동방정식은 다음과 같음

제어 시스템

- 제이 시스템 = 전기 시스템 + 기계 시스템 + (유압 시스템)

기계 시스템에서의 운동

- 회전 운동 rotation + 병진운동 translation

- 뉴톤의 운동 법칙이 적용됨

병진 운동

- 강체의 직선, 곡선 방향의 운동

- 변수 : 가속도, 속도, 변위

운동 방정식 equation of motion

- 물체에 가해지는 힘 f의 합 = 질량 M * 가속도 a와 같다.

힘-질량 시스템과 운동 방정식

- 아래의 힘-질량 시스템이 주어질때

- 이에 대한 운동 방정식은 아래와 같음.

힘-스프링 시스템

- 변위 y(t)는 힘 f(t)에 비례

힘-댐퍼 시스템

- 댐핑은 속도에 비례해서 제동을 주며, 댐핑힘 B과 속도의 관계는 아례와 같음

질량-스프링-댐퍼 시스템의 자유 물체도

- 아래의 질량-스프링-댐퍼 시스템이 주어질때 자유물체도는 우측과 같다.

- 이 시스템의 운동방정식은 다음과 같이 정리할 수 있다.

전기 시스템

- 제어기에 필수적. 아날로그나 디지털로 됨.

아날로그 소자

- 능동 소자, 수동 소자가 있음.

수동 소자

- 외부 별도 전원이 필요없는 소자

- 인덕터 L, 캐패시터 C, 저항 R이 있음

=> 수동 소자를 통해 극점, 영점이 0이아닌 다양한 전달함수를 만들 수 있음

* 0인 극/영점은 능동 소자 사용해야함

인덕터

- 전류의 변화량에 비례해 전압을 유도하는 코일

- 인덕터의 전류와 전압의 관계는 아래와 같음

캐패시터

- 직류를 가할시 전기를 저장

- 교류를 가할시 직류 성분을 차단

=> 노이즈 제거, 교류 통과, 불안정 전원을 해결하기 위한 용도

저항

- 단순 비례 관계

능동 소자

- 전압원, 전류원

- 증폭 기능을 가진 능동 소자는 종속 전압원, 종속 전류원으로 표현

트랜지스터 모델링

- 트랜지스터 등가 회로

연산 증폭기 모델링

미분기와 적분기

- 연산 증폭기로 0인 극점과 영점을 만들수 있음

전달 함수 구성 요소

- 미분기 derivative : G(s) = s. 영점이 0

- 적분기 integral : G(s) = 1/s.  극점이 0

- 비례기 proportional : G(s) = K

적분기와 비례기를 이용한 전달함수 예시

상태 선도 state diagram

- 상태 변수가 시간에 따라 변화하는 과정을 표현

상태 방정식과 출력 방정식

- 상태 방정식 state equation : 도함수 등 입력 상태 변수들의 선형 합으로 나타낸 방정식

- 출력 방정식 output equation : 출력 c(t)를 입력을 포함한 상태 변수들의 선형 합으로 나타낸 방정식

상태 공간 state space

- 동적 방정식 dynamic equation = 상태 방정식 state equation + 동적 방정식 dynamic equation

- 시스템을 동적 방정식 dynamic equation으로 표한한 것

라플라스 변환 laplace transform

- 시간 영역에 대한 시스템(함수)를 주파수 영역으로 변환하는것

*  푸리에 급수 : 주기 신호(함수)에 대한 주파수 영역으로의 변환

   푸리에 변환 : 비주기 신호(함수)에 대한 주파수 영역으로 변환

   라플라스 변환 : 비주기 발산신호의 주파수 영역 변환

역라플라스 변환 inverse laplace transform

- 주파수 영역의 함수를 시간 영역에 대한 함수로 변환

미분 방정식 differential equation

- 모든 물리 시스템은 미분 방정식으로 표현 가능함

- 종속 변수에 대한 독립 변수의 미분

- 미분 방정식에서의 미분이 상미분인지 편미분인지에 따라 분류됨

미분 방정식을 통해 해를 구하는 과정

1. 제어 시스템의 해를 구하기 위해 실제 현상을 미분 방정식으로 물리적 모델링

2. 미분 방정식을 라플라스 변환하여 대수 방정식으로 바꿈

3. 대수 방정식의 해를 구한 후 다시 역라플라스 변환

4. 시스템의 해를 구함

선형 미분 방정식 linear differential equation

- 종속변수 및 그 도함수가 1차이고, 각 계수(coefficient)가 독립변수 만의 함수

- 상수 계수 선형 미분 방정식

미분 방정식의 해- 일반해(보조, 동차해) general solution과 특수해 particular solution등이 있음- 완전해 complete solution = 일반해 + 특수해

제어 시스템과 미분 방정식의 해

- 시간 영역에서의 응답(완전 응답) = 고유 응답(과도 응답) + 강제 응답(정상 상테 응답)

- 미분 방정식의 특수 해 = 강제 응답, 정상상태 응답

- 미분 방정식의 일반 해 = 과도 응답, 고유 응답

- 미분 방정식의 완전해 = 완전 응답(시간 응답)

과도 응답 transient response, 고유 응답 natural response- 시간이 지나면서 사라지는 응답.

회로, 시스템의 특성을 나타냄

강제 응답 forced response, 정상상태 응답 steady state response

- 시간이흐른뒤 과도 응답이 0이되어 남는 시스템 응답. 외부의 입력에 의해 발생하는 응답

완전 응답 complete solution

- 과도 응답 + 정상상태 응답으로 시간 영역에서의 시스템의 응답

선형 시스템에서의 강제응답(정상상태 응답 특성)

- 입력 유형에 따라 출력 유형을 약간이나마 알 수 있음

- 입력이 상수  -> 출력도 상수

- 입력이 정현파 -> 출력도 정현파

제어 시스템에서의 고유응답 transient response

- 선형 미분방정식에서 입력이 0이며, 초기조건이 주어진 경우에 대한 응답

시불변 시스템 time invariant system

- 입력 r(t)와 출력 c(t)가 다음의 선형 미분방정식으로 나타내며 계수 a와 b가 상수인 경우. 시불변 시스템

전달 함수 transfer function

- 모든 초기조건이 0일때, 주파수 영역에서 출력 C(s)와 입력 R(s)의 비

- 단일 입력, 단일 출력에 대한 시스템의 특성을 나타냄

=> 시스템 안정성 등 중요한 정보들을 알려줌

전달 함수와 블록선도 block diagram

- 아래와 같이 입력과 출력에 대한 관계를 전달함수로 나타낸 그림

극점과 영점

- 극점 pole : 전달 함수 분모 다항식의 근

- 영점 zero : 전달 함수의 분자 다항식의 근

전달 함수로 얻을수 있는 시스템 특성

- 임펄스 응답 impulse response : 임펄스 신호에 대한 시스템의 반응

- 계단 응답 step response : 계단 신호에 대한 시스템 반응

- 주파수 응답 frequency response : 주파수 영역에서의 시스템 응답

일차 시스템 first order system

- 물탱크에 물을 채우는 시스템 처럼 종속 변수에 대한 독립 변수의 1차 미분으로 표현가능한 시스템

시스템의 시간 영역에 대한 응답 관련 용어

- 시정수 time constant : 1차 시스템(1차 회로)에서 과도 응답 특성을 나타냄. 정상상태의 63%에 이르는 시간

- 정착 시간 settling time : 정상상태의 98%에 도달하는데 걸리는 시간

- 과도 상태 transient state : 정착되기 이전의 상태

- 정상 상태 steady state : 정착 된 이후 상태

- 정상 상태 오차 steady state error : 기준 입력 r(t)와 정상 상태 출력 y(t)의 차이

- 오버슈트 overshoot : 시스템 응답이 최대치가 됬을때의 값

- 피크시간 peak time : 오버슈트일때의 시간

=> 제어기 controller는 시스템이 빠르게 정상상태에 수렴하도록 함

동적 시스템 dynamic system

- 시스템의 차수가 높아질 수록 입력에 대한 응답이 복잡해짐

-> 입력을 그대로 따르지 않는 시스템

이차 시스템 quadratic system

- 전달 함수가 이차 함수로 이루어진 시스템

이차 시스템 전달함수의 표준 형태 standard form

- 아래와 같으며, 여기서 전달 함수의 분모를 특성 방정식 characteristic equation이라 함

특성 방정식에서의 댐핑비와 고유주파수

- 댐핑비 damping ratio : 시스템이 얼마나 빠르게 수렴(감쇄되는지)를 나타냄

- 고유 주파수 natural frequency : 시스템이 얼마나 진동하는지를 나타냄

감쇄비 damping ratio

- 과감쇄, 오버슈트 overshoot : 댐핑비 zeta > 1

- 임계감쇄 critically damped : 댐핑비 zeta = 1

- 과소감쇄, 언더슈트 undershoot  : 댐핑비 zeta <1

극 영점도 pole-zero diagram

- 복소평면 상에서 극점과 영점을 나타낸 그림

- 극점은 x 영점은 o로 표시

극점의 위치에 따른 시스템 임펄스 응답

- 아래의 그림은 극점의 위치에 따른 시스템의 임펄스 응답

댐핑 비와 시스템 응답

주파수 응답 frequency response

- 주파수 영역에서의 시스템 응답

피드백 시스템

- 시스템 출력을 입력으로 되돌려(feedback)하여 오차를 줄여나가는 시스템

부궤환과 정궤환

- 부궤환 negative feedback : 기준 입력 - 출력

- 정궤환 positive feedback : 기준 입력 + 출력

피드백 전달함수가 상수인 일차 시스템

- 피드백 이득 K_F가 상수인 경우

- 폐루프 전달함수는 아래와 같다.

외란 disturbance

- 외부에 의한 원치 않은 입력. 바람, 잡음 등

직렬 제어 cascade control

- 외란의 영향을 받는 직렬 제어 시스템

시스템 system

- 기계, 전기 요소 component들의 모음

제어 control

- 시스템이 원하는 목표의 출력을 나도록 하는 행위

제어 시스템 control system

- 제어를 하려는 대상 시스템

입력, 출력

- 입력 input : 제어 시스템이 원하는 목표로 하도록 주는 지시

- 출력 output : 제어 시스템에 입력에 대한 결과

하부시스템 subsystem

- 제어 시스템만으로 부족한 부분을 보완해주기 위한 시스템

제어기 controller

- 제어 시스템이 원하는 출력이 나오도록 보완해주는 하부 시스템

ex. 우주선, 미사일, 조타 장치 등

제어기의 설계 design

- 제어 시스템을 해석하고 설계하는 행위

- 시간 영역 해석 : 임펄스 응답, 계단 응답, 근궤적법

- 주파수 영역 해석 : 보드 선도, 나이퀘스트 선도, 니콜스 선도 

제어 공학에서의 피드벡, 궤환 feedback

- 제어 시스템의 출력을 입력으로 되돌려주는것

- 기준 입력 r(t) - 출력 y(t) = 오차 e(t)

- 제어기는 오차 e(t)를 최소화 하기위해 동작함

폐루프 시스템 closed loop system

- 피드백으로 인해 입력과 출력간에 루프가 만들어지는 시스템

ex. 에어컨

개루프 시스템 open loop system

- 출력을 피드백하지 않아 오차가 보정되지 않는 시스템

ex. 선풍기

외란 disturbance

- 사용자 입력 이외에 시스템에 영향을 주는 외부 입력

ex. 비행기 제어 시스템에서의 외풍

안정성 stability

- 외란 발생시에도 제어시스템이 안정을 유지하는지에 대한 지표

- 출력을 피드백하여 안정성을 높이는데 이용됨

- 시스템의 안정성은 극점의 위치로 결정

현대에서의 제어 morden control engineering

- 자동차, 배 조타, 항공기, 우주선 등 모든 분야에 사용됨

동적 시스템 dynamic system

- 시간에 따라 변화하는 시스템

시스템 응답 system response

- 제어 시스템에 입력을 줄때, 시스템의 반응

- 시간영역, 주파수 영역에서의 반응으로 분류.

- 시간 영역 응답은 과도 응답과 정상상태 응답을 나누어서 볼 수 있음.

과도 응답 transient response

- 기준 입력 r(t)에서 시스템 출력이 얼마나 벗어났는지에 대한 응답

정상 상태 응답 steady state response

- 시스템이 과도기를 거친 후 출력과 가까워 진 시점에서의 응답.

시스템 설계 system design

- 제어 시스템이 안정성을 갖도록 하는 제어기 controller를 만드는것

제어 시스템 전반

1. 제어 개요

2. 수학적 백그라운드

3. 신호 흐름

4. 물리시스템 모델링

5. 상태 공간 해석

6. 피드백 제어 시스템

7. 안정성

8. 시간 응답

9. 근궤적 루트로커스

10. 주파수 응답

11. PID 제어

전달 함수 transfer function

- 선형, 시불변, 미분 방정식인 시스템이나 입출력 요소들간 관계의 특성을 구하기 위해 사용

- 선형, 시불변, 미분방정식 시스템의 전달 함수는 초기 상태가 0으로 가정 시, 출력의 라플라스 변환과 입력의 라플라수 변환의 비율로 구함

전달함수 구하기

- 아래의 식은 선형 시불변 시스템에서의 미분 방정식으로 y는 시스템 출력, x는 시스템 입력

$a_0a_0 \overset{(n)}{y} + a_1\overset{(n-1)}{y} + . . . + a_n y = b_0 \overset{(m)}{x} + b_1 \overset{(m-1)}{x} + . . . + b_m x$

- 전달함수는 초기상태가 0일때,  출력의 라플라수 변환과 입력의 라플라스 변환의 비율로 구함

전달함수 = G(s) = $\frac{L[output]} {L[input]} |_{0 초기상태}$

              = $\frac{Y(s)} {X(s)}$ = $\frac{b_0 s^{m} + b_1 s^{m-1} + . . . + b_m} {a_0 s^{n} + a_1 s^{n-1} + . . . + a_n}$

- 전달 함수 개념을 사용하면, s 영역에서 대수 방정식으로 시스템 동역학을 나타낼수 있습니다.

- 이 전달함수의 분모가 n차인 경우 이를 n차 시스템이라 부릅니다.

전달함수 사용시 고려사항

- 전달 함수는 선형, 시불변, 미분 방정식 시스템에서 사용할수 있지만 많이 사용되고 있습니다.

- 전달 함수를 사용시에 아래와 같은 고려사항들이 있습니다.

 1. 시스템의 전달함수는 단일 입력 변수에 대한 단일 출력 변수에 관한 미분 방정식을 나타내는 수학적 모델입니다

 2. 전달 함수는 시스템 고유의 성질로 입력의 크기나 성질에 독립적입니다.

 3. 전달함수를 알고 있다면, 다양한 입력에 대한 응답으로 시스템의 성질을 알수 있습니다.

 4. 전달 함수는 입력과 출력에 관한 요소들을 가지고 있으나 시스템의 물리적 구조에 대한 정보는 없습니다.

'

임펄스 응답

-초기 상태가 0일때, 단위 임펄스 입력에 대한 선형 시불변 시스템의 출력을 살펴봅시다.

- 단위 임펄스 함수가 입력으로 주어질때, 이 함수의 라플라스 변환은 1이므로 전달함수는 아래와 같습니다.

 Y(s) = G(s)

- 위 식에 대해 역 라플라스 변환을 수행하면 시스템의 임펄스 응답을 얻을수 있는데 G(s)에다가 역 라플라스 변환을 한것을 임펄스 응답이라 부르며, 임펄스 응답 g(t)는 선형 시불변 시스템에 단위 임펄스 입력을 준것에 대한 반응이라고 할수 있습니다.

$L^{-1} [G(s)] = g(t)$

제어 시스템과 수학적 모델링

- 수학 용어로 동역학 시스템을 모델링 할수 있어야함

- 이 시스템의 동역학적 특성을 분석할수 있어야 함.

동역학 시스템의 수학적 모델

- 시스템의 동역학을 나타내는 여러개의 방정식들로 정의.

- 하지만 시스템에대한 수학적 모델링은 하나가 아니라 다양한 방법으로 표현 가능

동역학 시스템의 종류

- 기계적 시스템

- 전기적 시스템

- 유체 시스템

=> 다 미분 방정식으로 표현

미분 방정식 구하기

- 각 시스템에 대한 물리적 법칙으로 얻을 수 있음

- 기계적 시스템의 경우 뉴턴 법칙

- 전기적 시스템에선 키르히호프의 법칙

수학적 모델

- 다양한 형태로 수학적 모델을 만들 수 있음.(어느 시스템이냐, 상황에 따라)

- 최적 제어 문제에선 상태 공간 표현법이 좋음

- 입력 신호에 대한 과도 응답이나 주파수 응답 분석,  선형, 시뷸변 시스템인경우 전달함수 모델이 좋음

간결함과 정확도

- 수학적 모델링을 구할때 모델을 간결하게 할지 정확하게 할지 절충해야하며, 간단하게 하기위해 시스템 물리적 특성일부를 무시해야함.

- 선형 수학적 모델링을 한다고 하면, 비선형적인 요소들과 파라미터들을 제거 필요

- 제거한 속성의 영향력이 작다면, 실제 물리적 시스템과 수학적 모델링 사이에서 차이가 크지않을것임

선형 시스템 linear system

- 중첩 superposition의 원리가 적용되는 시스템을 선형 시스템.

- 중첩의 원리는 서로 다른 두 변수를 동시에 주었을때 나온 응답과와 두 변수 개별 응답의 합이 동일한 경우.

- 선형 시스템은 여러 입력에 대한 응답을 단일 입력들의 응답으로 계산할수 있음.

=> 중첩의 원리를 사용해 복잡한 식을 간단히 해를 구할수 있는 선형 미분 방정식으로 바꿀수 있다.

선형 시불변 시스템과 선형 시변 시스템

- 시스템의 계수들이 상수이고, 독립 변수들로 이루어진 경우 미분 방정식은 선형.

- 선형 시불변 시스템 : 선형 시불변 미분 방정식을 요소하는 동역학 시스템

- 선형 시변 시스템 : 계수가 시간에 대한 함수인 미분 방정식으로 표현된 시스템

실제 물리적 시스템과 모델링 사이의 오차 제거

1. 가능한 에러 범위 설정

2. 이 범위를 넘지 않는 제어기 설계

   -> 설계된 제어기 시스템이 안정하다고 볼수 있음

=> 강인 제어 이론이라 함

강인 제어 이론 robust control theory

- 주파수 응답과 시간 영역에서의 방법을 둘다 사용

- 수학적으로 매우 복잡

용어들

1. 제어 변수, 제어 신호, 조정 신호

- 제어 변수 controlled variable : 관측하거나 제어하려는 상태나 값

- 제어 신호 control signal, 조정 신호 manipulated variable : 제어기를 사용하여 제어 변수의 값에 영향을 주는  값, 상태

- 제어 control : 시스템의 제어 변수 값을 관측하고, 목표 값으로 도달하도록 편차를 줄이는 제어 신호를 보내는 것

2. 플랜트

- 특정한 일을 수행하는 장비

- 플랜트로 우주선이나 화학 반응기 같은 물체를 제어할것임.

3. 프로세스

- 연속된 작업들 혹은 특정 결과를 얻도록 하는 일련의 변화 과정들

4. 시스템

- 특정한 목표를 이루기 위해 함께 동작하는 요소들의 모임

- 시스템은 물리적인 개념뿐만이 아니라 추상적인 개념으로도 사용될수 있음.

 * ex. 경제학에서 동적인 변화 현상

=> 물리학, 생물학, 경제학 같은 분야에서도 시스템이 사용될수 있음.

5. 요란 disturbance

- 시스템 결과에 악영향을 주는 신호

- 요란이 시스템 내부에서 발생 -> 내부 요란

- 시스템 외부에서 발생하여 입력으로 들어옴 -> 외부 요란

6. 피드백 제어 feedback control

- 요란이 존재할때 시스템의 출력과 기준 입력 사이 차이를 줄여주도록 하는 제어 작업

- 예측할수 있거나 알고 있는 요란은 시스템 내부에서 보상될수 있으므로 예측할수 없는 요란들이 입력으로 들어옴.

온도 제어 시스템의 예시

1. 전기 난로는 내부의 온도계로 (아날로그) 기온을  측정

2. 아날로그 기온은 AD 변환기로 디지털 온도로 변환

3. 디지털 온도는 인터페이스를 통해 제어기 입력으로 들어감

4. 입력된 디지털 온도는 기존에 입력으로 설정한 온도와 비교

5. 현재 온도와 기준 온도 사이의 차이가 발생 시, 제어기는 히터에 신호를 보냄

6. 증폭기 amplifier로 신호가 증폭되고, 릴레이를 통해 전기 난로가 목표 값에 도달하도록 제어됨.

피드백 제어 시스템

- 출력과 기준 입력을 비교하고, 그 오차를 제어에 사용하는 시스템

  ex. 방 온도 제어

- 사람의 신체와 같이 공학 이외 분야에서도 피드백 제어가 많이 이용됨.

폐루프 시스템 closed loop control system

- 피드백 제어 시스템은 폐루프 제어 시스템이기도 함

- 폐루프 제어 시스템에서 오차 신호로 구동함.

- 오차를 줄이도록 제어기가 동작하여 시스템 출력이 원하는 값에 도달

=> 즉, 폐루프 제어는 시스템 오차를 줄이도록 피드백 제어 동작을 수행한다고 할 수 있음.

개루프 제어 시스템 open loop control system

- 시스템 출력이 제어 동작에 영향을 주지 않는 시스템

 => 개루프 시스템의 출력은 측정하지 않음 + 입력과 비교해서 피드백 되지 않음.

 * ex. 식기 세척기, 세탁기 등(출력을 측정하지 않고, 그냥 세척만 함)

폐루프 시스템과 개루프 시스템의 차이

- 폐루프 시스템의 장점은 피드백 제어를 사용하므로 시스템 응답이 외부 요란이나 내부 변화에 덜 민감

- 값싸고 정밀하지 않은 장치를써도 플랜트를 이용해 정확한 제어가 가능함, 개루프 시스템은 불가능함

- 개루프 시스템은 시스템 안정성이 주요 이슈가 아닌 경우 사용됨

- 시스템 안정성이 중요한 경우 폐루프가 사용. 오차를 줄여나가면서 진폭 변화와 상수 진동이 발생

개루프 시스탬의 장점

1. 만들거나 유지하기 쉽다

2. 폐루프보다 싸다

3. 안정성 문제를 고려안한다.

4. 출력 측정이 힘들때 편하다

개루프 시스템 단점

1. 요란이 생기거나 변화시 오차가 발생 -> 출력이 원해던 목표치와 달라진다

2. 일정한 퀄리티로 원하는 값을 유지하려면, 매번 재조정이 필요하다.