추정, 추론 estimation, inference
- 표본 집합 데이터들로 정확하지는 않으나 값을 구하나는 행위
패턴인식에서의 추정
- 수집된 표본으로부터 확률 밀도 함수를 추정은 패턴을 인식하기 이해서 매우 중요
- 유한개의 표본들로 클래스별 확률 밀도 함수 추정해야함
베이즈 정리
- 사후확률 계산하려면 우항의 우도, 사전확률을 알아야함.
- 사전확률 : 이미 알고있는것으로 정의될수 있음
- 우도 : 해당 클래스의 확률 밀도 함수로 표본 데이터를 이용하여 추정 필요

데이터 밀도 추정 방법
- 모수적 방법 parametric method
주어진 데이터 집합(샘플 데이터들)이 이루는 확률 밀도 함수가 가우시안 같은
특정 형태로 이루어진것을 가정하고, 확률밀도 함수의 평균, 공분산 등의 파라미터 추정한는 방법.
=> 샘플 데이터가 특정 분포를 따른다 가정하여, 그 분포의 파라미터 추정 (ex. 최우추정법 MLE)
- 비모수적 방법 non parametric method
주어진 데이터가 아무 분포를 따르지 않고, 데이터로 직접 밀도 함수를 구하는 방법.
* ex. 히스토그램, KNN, KDE 커널 밀도 추정
최우추정법 최대 우도 추정, MLE Maximum Likelihood Estimation
- 아래와 같이 M개의 파라미터 집합과 확률 밀도 함수 P(x | Theta)로 관측된 표본 데이터 집합 x가 주어질때 파라미터들을 추정하는 방법
=> 샘플 데이터로 특정 확률 분포의 파라미터 추정

- 어느 프로세스로 발생된 데이터로 이루어진다면, 전체 표본집합은 결합확률 밀도로 다음과같음.

- 위 식에서 P(x|Theta)는 파라미터 Theta를 따르는 주어진 데이터 집합의 우도 함수.
- 위 함수는 확률 함수. 가장 큰 확률 갑을 구하는 Theta를 hat{theta}로, 우도 함수의 곱을 합으로 바꾸게 log를 하자
=> 이 식은 로그 우도 함수 log likelihood function.
=> 로그 우도 함수를 최대로 하는 파라미터 hat{theta}가 미지의 파라미터를 가장 잘 추정해냄


로그 우도 최대화 maximization of log likelihood
- 로그 우도를 최대화 하기 위해서 Theta에 대해서 편미분 하자.

- 아래의 그림은 1차원 데이터에 대해 많은 후보 확률 분포가 나타냄.

- 다음 그림은 결합 밀도 함수로 구한 우도 함수 p(D|Theta) (D는 dataset)
* 우도를 최대화 하는 파라미터에 hat{theta} 표기가 됨
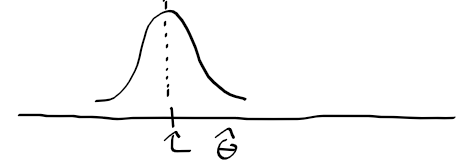
- 다음 그림은 로그 우도 함수. 최우도 hat{theta}의 위치가 우도인 경우와 동일함

MLE 최대 로그 우도 추정법으로 최대 로그 우도 구하기
- 파라미터 벡터를 다음과 같이 가정

- 로그 우도의 그라디언트를 구하면
* hat{theta}가 로그 우도를 최대화 하는 파라미터

최우 추정하기
1. 표본 집단의 로그 우도 구하기

2. l(theta)를 모든 파라미터로 편미분 한 후, 우항을 0으로 하여 최우 방정식으로 만듬

3. 연립 방정식을 풀어 해를 구한다.
4. 해 중에서 최대값을 추정 파라미터 hat{theta}로 쓴다.
가우시안을 따르는 샘플 데이터로부터 파라미터를 최우추정법으로 추정하기
- 표본 데이터가 단변량이라 가정

- 우리는 이 샘플 데이터가 가우시안 분포를 따른다 가정하고 가우시안 분포의 파라미터를 추정할 것임
=> 단변수 가우시안 확률 밀도 함수의 로그 우도는 아래와 같음.

- l(theta)의 그라디언트는 다음과 같음
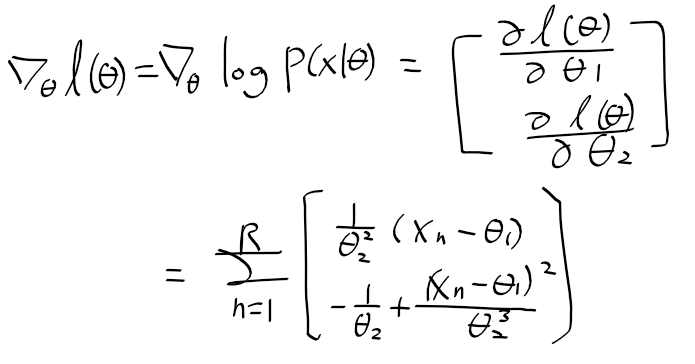
- 그라디언트 우항을 0으로 하여, 최우 방정식을 만들자. 로그 우도를 최대로하는 첫번쨰 파라미터는 표본평균

- 로그 우도를 최대로하는 두번쨰 파라미터는 표본 분산

- 결론 : 주어진 샘플 데이터의 평균과 표본 분산이 로그 우도를 최대로 하는 파라미터
'수학 > 공업수학, 확률' 카테고리의 다른 글
| 확률 - 2. 고전적 확률과 공리적 확률 (0) | 2020.08.07 |
|---|---|
| 확률 - 1. 확률 개요 (0) | 2020.08.07 |
| 통계 - 13. 판별함수 (0) | 2020.08.04 |
| 통계 - 12. 베이즈 위험을 이용한 결정 규칙들과 다중 클래스 결정 규칙 (0) | 2020.08.04 |
| 통계 - 11. 베이즈 위험 (0) | 2020.08.04 |