728x90

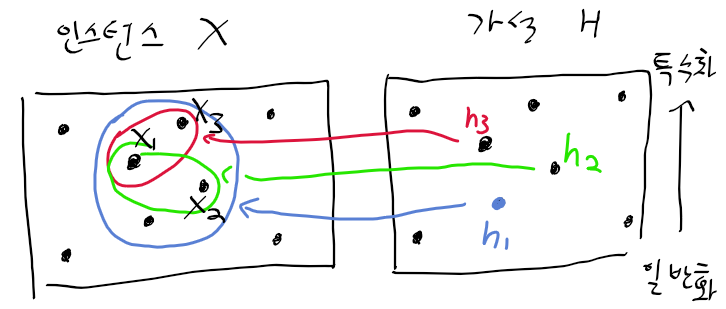
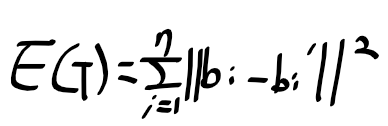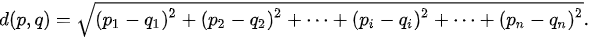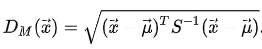 이번에 프로젝트로 위성 사진을 시멘틱 분할하는 어플리케이션을 준비하게 되었다. 베이스라인 모델로 U-Net 같은 것들을 사용하면 된다고 하더라. 일단 이전에 시멘틱 분할 모델인 FCN이나 U-Net 같은 모델 논문을 잠깐 간단히 보기는 했지만 그렇게 잘 와닿지는 않았다.

 

 아무튼 지금나는 시멘틱 세그먼테이션을 하기 위해서 저런 모델을 사용한다는 사실만 알고, 데이터셋을 어떻게 준비하는 지 모델을 만들어서 준비한 데이터셋으로 학습하고 돌리는지 까지는 잘 모르는 상태였다. 그래서 잠깐 구글링으로 U-Net으로 별도의 데이터셋을 훈련하는 방법, 프로젝트에 관해서 검색 해보았는데 자세히 보지는 못했지만 Palliwi라는 분이 잘 정리해서 미디움에다가 올려놓으셨더라.

 

pallawi-ds.medium.com/semantic-segmentation-with-u-net-train-and-test-on-your-custom-data-in-keras-39e4f972ec89  

 

Semantic segmentation with U-Net- train, and test on your custom data in Keras

What is semantic segmentation?

pallawi-ds.medium.com

 

 주의 깊게 본다면 이해할 수 있을것 같긴한데 내용 앞부분을 보면서 잠시 FCN, U-Net 모델에 대해서 조금 더 깊이 이해할 필요성을 느꼈다. 이전에 여러번 초록 정도는 보고, 이해하려고 뭔가 속시원하게 파악하지는 못하다보니 이번에 다시 FCN 부터 다양한 국내 블로그 정리 글을 찾아보았는데 가장 먼저 라온 피플에서 작성한 글을 보았다. 보면서 나도 이렇게 잘 좀 정리하고 싶은데 왜 이렇게 힘들까 ㅠㅜ. 지난번에 ResNet도 깔끔하게 정리해봐야지 해놓고 계속 미뤄두네 ;;

 

m.blog.naver.com/laonple/220958109081

 

[Part Ⅶ. Semantic Segmentation] 3. FCN [1] - 라온피플 머신러닝 아카데미 -

Part I. Machine Learning Part V. Best CNN Architecture Part VII. Semantic Segmentat...

blog.naver.com

 

라온 피플의 FCN에 대한 설명 1

 이 글에서는 우선 FCN이 언제 나오고 얼마나 열광 받고 있는지 부터 시작하고 있다. 그리고 분류, 검출, 시멘틱 세그먼테이션과 같이 컴퓨터 비전 분야의 문제들을 소개하면서 각각 문제 모델의 특징들을 알려주는데, 이런 내용은 여러번 보았고 알곤 있었지만 뭔가 허전함? 깔끔하게 정리가 잘 안됬는데 이런 내용들 처럼 잘 정리하고싶다 ㅜㅜ

 

 아무튼 FCN의 Fully Convollution layer/ 1 x 1 Convolution의 장점에 대해서 소개하는데 이 방법이 나는 FCN에서 처음으로 사용된 것인줄 알았지만 이전에 잠깐 있다고만 들었던 OverFeat 모델에서 사용되었다고 하더라. 하지만 OverFeat에서는 분류, 검출에서만 사용했다 하고, FCN이 시멘틱 세그먼테이션 용도로 1 x  1 conv가 사용된 경우라고 한다.

 

 여기서 말하는 1 x 1 Convolution의 장점으로는 기존의 분류 모델이나 검출 모델에서는 뒤에 고정 크기의 벡터를 만드는 완전 연결 레이어가 존재하여 입력 크기의 제한을 받는다고 한다. 아마 입력 크기가 클수록 고정 크기의 입력 벡터로 정리하려고 많은 정보들을 정리할 수 없고, 완전 연결 계층에서 연산을 하기 위해 Flatten 할 필요가 없어지니 기존의 공간적 정보가 사라지는 것을 방지 한다는 점에서 영상 제한이 사라진다고 하는것 처럼 보인다. 

 

 이 다음으로는 디컨볼루션을 이용한 업샘플링에 대해서 설명해주고 있다. 업샘플링을 하는 이유는 여러 레이어들을 거쳐가면서 피쳐맵의 공간적 크기가 줄어드는데 이를 기존의 입력 크기와 동일하게 맞춰주기 위함인데, 간단하게 업샘플링을 한다면 opencv의 resize함수처럼 양선형 보간법을 사용하면 되겠지만, 여기서는 end-to-end 학습을 통해 구하며 backward convolution(deconvolution)을 사용한다고 말한다. 

 

 하지만 마지막 레이어에서 너무 작아진 피쳐맵만 가지고 deconv로 크기를 키우면 중간에 존재하던 디테일한 정보들이 사라지기 때문에 중간 레이어로부터 스킵커넥션을 통해 보강시킨다고 한다. 이걸 tf로 어떻게 표현하는지는 잘 모르겠지만 skip layer를 추가시킬수록 더 정교한 예측을 만드는 것으로 이 글이 마쳤다. 라온 피플에서 FCN 모델에 대해 추가적인 설명을 하니 다음 글도 봐야겠다.

300x250
저작자표시

'인공지능' 카테고리의 다른 글

AINIZE를 활용한 ML 프로젝트 배포  (0) 2021.03.26
[인공지능및기계학습]02.4 엔트로피와 정보 이론  (0) 2021.01.14
[인공지능및기계학습]02.3 결정 트리 개요  (0) 2021.01.13
[인공지능및기계학습]02.머신러닝의 기반들  (0) 2021.01.08
[인공지능및기계학습]01.동기부여 및 기초  (0) 2021.01.07
728x90

AINIZE

- 오픈 소스 프로젝트를 간편하게 배포하는 툴

ref : ai-network.gitbook.io/ainize-tutorials/

 

DevOps(Development Operation)

- IT 제품 개발 사이클을 의미

1. 프로토타이핑

2. 테스트

3. 패키징

4. 배포

5. 실행

6. 반복

=> MLOps(Machine Learning Operation)을 구현하자.

 

MLOps 준비

1. ML 프로젝트를 웹(flask)으로 연동 준비

2. 도커화

3. Ainize로 프로젝트 배포

 

포크할 ML proj

github.com/minsulee2/mnist-mlp-app

- 위 저장소의 숫자 인식 ml proj를 클론 받아 웹 연동 후 ainize로 배포할 예정

 

 

 

파일 구조

 

 

 

Flask 서버 코드 작성(server.py)

from flask import Flask, render_template, request, Response
from PIL import Image
from image_preprocessor import preprocess
from mnist_mlp import load_keras_model, predict_number

model = load_keras_model()
app = Flask(__name__, template_folder="./templates/",
        static_url_path="/images", static_folder="images")

@app.route("/")
def index():
    return render_template("index.html")

@app.route("/healthz", methods=["GET"])
def healthCheck():
    return "", 200

@app.route("/image", methods=["POST"])
def get_result():
    if request.method == "POST":
        width, height = 28, 28
        try:
            source = Image.open(request.files["source"])
            adjusted_img = preprocess(source, width, height)
            res = predict_number(model, adjusted_img, width, height)
        except Exception as e:
            print("error : %s"%e)
            return Response("fail", status=400)
    return str(res)

if __name__=="__main__":
    app.run(host="0.0.0.0", port="80", debug=True)

 

index.html

- 작업 폴더에 템플릿 폴더를 만들어 그안에 배치

- (workspace)/template/index.html

<HTML>
	<head>
		<meta charset="utf-8">
		<meta name="viewport" content="width=device-width, initial-scale=1, shrink-to-fit=no">
		<link rel="stylesheet" href="https://stackpath.bootstrapcdn.com/bootstrap/4.4.1/css/bootstrap.min.css"
			 integrity="sha384-Vkoo8x4CGsO3+Hhxv8T/Q5PaXtkKtu6ug5TOeNV6gBiFeWPGFN9MuhOf23Q9Ifjh"
			 crossorigin="anonymous">

		<title>Handwritten Number Reader</title>
		<style>
			.img{
				height: 250px;
			}

			figure{
				display: inline-block;
				text-align:center;
			}
		</style>
	</head>
	<body>
		<div class="container">
			<div class="jumbotron mt-3">
				<h1>digit reader</h1>
				<a>github repo</a>
				<a href="https://github.com/JeongChanDo/mnist-mlp-app">mnist</a>
				<br>
				<hr class="solid">
				<div id="sampleBox">
					<figure>
						<img class="img" src="./images/2.png">
					</figure>
				</div>
				<br>
				<div id="input img">
					<label for="source">source num img : </label>
					<input type="file" id="source" style="margin-right: 10px; margin-bottom: 10px;">
					<button id="submit" type="submit" class="btn btn-primary btn-lg" style="margin-left: auto;"> run</button>
				</div>
				<div id="resultbox" style="margin-left: auto; margiin-right: auto;">
					<p id="errorbox"></p>
					<p id="result"></p>
				</div>
				<script>
				  document.getElementById("submit").onclick = () => {
				       var formData = new FormData();
				       var source = document.getElementById('source').files[0];

				       formData.append('source', source);

				       fetch(
					   '/image',
					   {
					       method: 'POST',
					       body: formData
					   }
				       )
				       .then(response => {
					   if (response.status == 200) {
					       return response.text();
					   }
					   else {
					       throw Error("Loading image error");
					   }
				       }).then(text => {
					   document.getElementById('result').innerText = text;
				       }).catch(e =>{
					   document.getElementById("errorbox").innerHTML = e;
				       });
				   };
				</script>
			</div>
		</div>
	</body>
</HTML>

 

Dockerfile 수정

FROM tensorflow/tensorflow:latest-gpu

RUN apt-get update
RUN apt-get install -y libgl1-mesa-dev
RUN pip install keras numpy pillow flask

COPY . .

EXPOSE 80
ENTRYPOINT ["python"]
CMD ["server.py"]

 

mnist_mlp.py 수정

from __future__ import print_function

import keras
import numpy as np
from keras.datasets import mnist
from keras.models import Sequential, load_model
from keras.layers import Dense, Dropout
from keras.optimizers import RMSprop
from keras.preprocessing import image

def load_keras_model():
    model = load_model("models")
    return model

def predict_number(model, img, width, height):
    test_img = image.img_to_array(img)
    test_img = test_img.astype("float32")
    test_img = test_img.reshape(width, height)
    test_img /= 255
    test_img = test_img.reshape(1, width * height)
    res = model.predict(test_img, batch_size=1)
    return np.argmax(res)

 

 

도커 이미지 빌드 및 실행

- localhost/healthz로 서버가 잘 살아있는지 확인 가능

docker build -t mnist-mlp-app .
docker run -p 80:80 mnist-mlp-app

 

동작 확인

http://localhost/

에 들어가서 아래의 이미지 업로드

num4.png
0.01MB

 

 

 

 

ainize를 이용한 배포

- ainize.ai/dashboard

 

 

 

 

300x250
저작자표시

'인공지능' 카테고리의 다른 글

Sementic Segmentation 준비기 1  (0) 2021.05.12
[인공지능및기계학습]02.4 엔트로피와 정보 이론  (0) 2021.01.14
[인공지능및기계학습]02.3 결정 트리 개요  (0) 2021.01.13
[인공지능및기계학습]02.머신러닝의 기반들  (0) 2021.01.08
[인공지능및기계학습]01.동기부여 및 기초  (0) 2021.01.07
728x90

한 특성만 보는게 아니라 여러개를 보는 경우 특징을 위주로 보는게 좋을까?

신용카드 발급 여부 문제에서 계속 이어나가보자

 

엔트로피 entropy

- 어떤 특성이 더 좋은것인가?를 보여주는 지표

 -> 아까 본 A9의 속성으로 분할한 경우 속성 값이 t일때 284개가 긍정, 77개가 긍정

    => 속성 값이 t일때 긍정이 나올 가능성이 크므로 A1보다 불확실성이 작다고 할 수 있음.

 -> A1속성으로 분할한 경우 속성 값이 a일떄 98개가 긍정, 112개가 부정.

    => 긍정과 부정이 나올 수가 비슷하므로 불확실성 uncertainty이 크다고 할수 있음.

 

- 불확실성의 측정 지표로서의 엔트로피

 -> 하나의 특징, 속성을 확률 변수 random variable로 볼수 있다!

    ex. 항상 3만 나오는 주사위 -> 항상 확실하므로 불확실성이 없다.

    ex. 모든 면이 1/6확률로 나오는 주사위 -> 불확실성이 존재하다.

 -> 엔트로피가 크다 = 불확실성이 크다

 -> 아래는 엔트로피를 구하는 함수.

- 조건부 엔트로피를 구하자

 -> 특징이 주어질때 해당 클래스의 엔트로피를 구하자.

 

 

정보 게인 Information Gaion

- 이제 확률변수 A1과 A9의 엔트로피를 구할수가 있겠다.

- 조건부 엔트로피를 통해 특징이 주어질때 클래스별 엔트로피를 구할수가 있다.

- Y라는 클래스의 엔트로피를 위의 엔트로피 구하는 식을 통해 구햐보자

 

 

- A1, A9 특징이 주어질때 Y가 나올 엔트로피를 구해보자

 

- 우리가 원하는 것은 클래스별 엔트로피를 불확실성을 없애는 방향으로, 확실한 방향으로 만들어야 한다.

 -> 어떤 정보를 추가해야 불확실성이 사라질까?를 파악하기위헤 조건부 엔트로피를 사용

    => A1의 정보를 주었을때 엔트로피가 어떻게 되는가 -> H(Y | A1)

    => A9의 정보를 주었을때 엔트로피가 어떻게 되는가 -> H(Y | A2)를 알아야 한다.

 

- 어떤 클래스 엔트로피가 주어졌을때, 어떤 속성 특징을 사용한 경우(조건부) 해당 클래스의 엔트로피가  클래스의 엔트로피가 얼마나 크게 변하였는가

 -> 원래 클래스 엔트로피와 특징이 주어진 경우 엔트로피가 얼마나 크게 차이나는가 = 정보 게인

=> 불확실성이 작은 A9 속성이 정보 게인이 크다.

 

 

 

신용카드 발급 데이터를 이용한 결정 트리 만들기

1. A1 부터 A15까지 모든 정보 게인을 측정하자

2. A9이 제일 좋구나(정보 게인이 크다)-> A9으로 트리 루트를 사용하여 분리.

3. 분리된 데이터로 다음에는 어느 속성의 정보게인이 가장 큰가를 판단하여 노드 분리

4. 3번 과정을 여러번 반복

5. 결정 트리 완성

 

 

 

결정 트리의 문제

- 모든 속성을 다루는 큰 결정 트리를 만든 경우의 문제

 -> 학습된 경우는 처리할수 있으나 현실에 존재하는 노이즈나 이상한 경우를 대응하지 못함.

- 아래의 그림을 보면 x축은 트리의 크기, y는 정확도를 보야주고 있음.

 -> 결정트리가 커질수록 파란선(훈련 데이터)은 높아지나, 빨간 선(테스트 데이터)은 피크를 지난 후 정확도가 내려감

  => 가지고 있는 데이터에 정확하게 만들수 있으나 학습되지 않은 세세한 경우를 다루지 못해 떨어진다.

 

300x250
저작자표시

'인공지능' 카테고리의 다른 글

Sementic Segmentation 준비기 1  (0) 2021.05.12
AINIZE를 활용한 ML 프로젝트 배포  (0) 2021.03.26
[인공지능및기계학습]02.3 결정 트리 개요  (0) 2021.01.13
[인공지능및기계학습]02.머신러닝의 기반들  (0) 2021.01.08
[인공지능및기계학습]01.동기부여 및 기초  (0) 2021.01.07
728x90

규칙 기반 머신러닝의 한계

- 우리가 살고 있는 현실에는 노이즈가 존재하여 관측되므로 원하는 결과를 구하기 힘듬.

 

우리가 필요한 것들

- 노이즈가 있는 데이터에 더 강건해야하는 방법

- 가설을 더 명확하게 설명할수 있는 방법

 

규칙 기반 머신러닝 기법으로 나가 놀지 여부를 결정 트리로 표현 하는 경우

 

 

 

신용 평가 데이터셋을 사용한 머신 러닝

- 신용카드를 발급해줄지 말지를 이 데이터셋으로 판단해보자

- 690개의 인스턴스, 307개의 긍정 케이스(신용 카드 발급)

- ref : http://archive.ics.uci.edu/ml/datasets/Credit+Approval

- 신용 평가 정보 Attribute Information:

A1: b, a.
A2: continuous.
A3: continuous.
A4: u, y, l, t.
A5: g, p, gg.
A6: c, d, cc, i, j, k, m, r, q, w, x, e, aa, ff.
A7: v, h, bb, j, n, z, dd, ff, o.
A8: continuous.
A9: t, f.
A10: t, f.
A11: continuous.
A12: t, f.
A13: g, p, s.
A14: continuous.
A15: continuous.
A16: +,- (class attribute)

 

 

 

A1속성만으로 판단하는 경우

- A1 속성 값이 a인 경우 98개가 긍정이고, 112개가 부정

- A1 속성 값이 b인 경우 206개가 긍정, 262개가 부정

- A1 속성 값이 알수없음 ?인 경우 3개가 긍정, 9개가 부정

   => 가능한 모든 경우의 총 긍정 307, 총 부정 383

=> A1 속성만으로는 긍정과 부정 여부를 잘 분류하지 못한다고 볼수 있다. 거의 50:50 비율로 판별하므로

 

A9 속성 만으로 판단하는 경우

- A9 속성 값이 t인 경우 284개가 긍정, 77개가 부정

- A9 속성 값이 f인 경우 23개가 긍정, 306개가 부정

=> A9 속성이 t일때 긍정을 많이 찾고, f일때 부정을 많이 찾는다. => A1 속성보다는 잘 분류해낸다.

 

300x250
저작자표시

'인공지능' 카테고리의 다른 글

AINIZE를 활용한 ML 프로젝트 배포  (0) 2021.03.26
[인공지능및기계학습]02.4 엔트로피와 정보 이론  (0) 2021.01.14
[인공지능및기계학습]02.머신러닝의 기반들  (0) 2021.01.08
[인공지능및기계학습]01.동기부여 및 기초  (0) 2021.01.07
컴퓨터 비전 & 패턴 인식 - 32. 아웃라이어에 대처하는 기하 변환 방법  (0) 2020.12.16
728x90

목표

  • 머신러닝의 고전적 방법들을 배워보자
    • 규칙 기반 방식 rule based approach
    • 고전 통계적 방식 classical statisitc approach
    • 정보 이론 방식 information theory approach
  • 규칙 기반 머신러닝
    • 어떻게 특성화되거나 일반화 할수 있는 규칙을 찾는지 알아보자
    • 왜 이러한 규칙이 쉽게 깨지는지 알아보자
  • 결정 트리
    • 어떻게 훈련 데이터셋으로 결정 트리를 만들어낼까
    • 왜 새로운 데이터셋에 대해 트리가 약한 분류기가 될까.
  • 선형 회귀
    • 어떻게 훈련 데이터셋으로 파라미터를 추론하는가
    • 왜 피처 설정이 한계를 가지는가.

규칙 기반의 머신 러닝 rule based machine learning

  • 완벽한 세상에서의 규칙 기반의 머신 러닝 : 아래와 같은 가정을 할때
    • 관측 에러가 없고, 항상 일관된 관측 결과를 구할 수 있다.
    • 관측 결과에 확률적인 영향, 임의에 의한 영향이 존재하지 않다.
    • 시스템을 설명할수 있는 모든 정보를 얻었다.
  • 사람이 기상을 관측해서 나가서 운동할수 있는지의 여부, 규칙을 이용한 머신러닝으로 판단하자.
    • <기상, 온도, 습도, 바람, 수온, 기상 변화> 정보를 얻고, 이 정보로 운동할수 있는지 예측하자.

함수 근사 function appraoximation

  • 머신 러닝이란?
    • 머신 러닝은 더 나은 근사 함수를 만드는 작업이라 할 수 있다.
  • 이전에 정의한 완벽한 세상에서 운동을 할수 있는지의 여부를 다루자.
    • 인스턴스 X
      • 피처 O : <화창, 따뜻, 보통, 강함, 따뜻, 같음>
      • 라벨 Y : <운동 가능>
    • 훈련 데이터셋 D
      • 인스턴스 관측 집합
    • 가설 H
      • X로 Y를 얻을수 있는 어떤 함수, 가설들이 존재할까?
      • h_i : <화창, 따듯, ?, ?, ?, 같음> -> 운동 가능
      • 얼마나 많은 가설이 존재할까?
    • 타겟 함수 c
      • 피처와 라벨로 알수 없는 타겟 함수. 가설 H의 목표가 되는 함수.

함수 근사를 시각적으로 살펴보기

  • 다음의 인스턴스 x가 존재할때,
    • x1 : <화창, 따뜻, 보통, 강함, 따뜻, 같음>
    • x2 : <화창, 따뜻, 보통, 약함, 따뜻, 같음>
    • x3 : <화창, 따뜻, 보통, 강함, 따뜻, 변함>
  • 아래의 가설 H가 존재한다고 하자
    • h1 : <화창, ?, ?, ?, 따뜻, ?> -> 기상이 화창하고, 수온이 따뜻한 경우 -> 운동 가능
    • h2 : <화창, ?, ?, ?, 따뜻, 동일> -> 기상이 화창하고, 수온이 따뜻하며, 기상 변화가 없을때 -> 운동 가능
    • h3 : <화창, ?, ?, 강함, 따뜻, ?> -> 기상이 화창하고, 바람이 강하며, 수온이 따뜻할 때 -> 운동 가능
      • x2를 h3 가설을 기준으로 판별시 -> 운동 불가로 판단.
      • x3는 h3 가설을 기준으로 판별 시 -> 운동 가능로 판단.
  • 어느것이 가장 나은 함수 근사, 가설이라 할수 있을까?
    • 일반화와 특수화에 달린 문제
    • 가설 h1은 약한 조건을 가진 가설(일반화 가능한 가설)
    • 가설 h3은 강한 조건을 가진 가설

규칙 기반 알고리즘 살펴보기

S 탐색 알고리즘(Find S Algorithm)

  • 최적의 가설 h를 구한다.

  • 데이터셋 D에서 모든 인스턴스 x에 대해

    • x가 긍정이라면, 위 예시를 들면 운동 가능하다면
      • 모든 피처 f에 대해, 피처와 가설이 동일하면 -> 아무것도 하지 않음.
        • ex ) 가설 h3의 기상 특징이 화창, 인스턴스 x_i의 기상 특징이 화창인 경우 아무런 동작을 하지 않음
      • 해당 인스턴스 x의 피처 f와 가설의 f가 동일하지 않다면 -> 가설에 포함시킴
        • ex ) 가설 h3의 기상 변화특징이 동일, 인스턴스 x_i은 변화인 경우 다르므로 합집합 가설을 구함.

  • 다음의 인스턴스 x가 주어지고

    • x1 : <화창, 따뜻, 일반, 강함, 따뜻, 동일>
    • x2 : <화창, 따뜻, 일반, 약함, 따뜻, 동일>
    • x4 : <화창, 따뜻, 일반, 강함, 따뜻, 변화>

  • 다음의 가설이 주어지면

    • h0 = <0, 0, 0, 0, 0, 0>
    • h1 = <화창, 따뜻, 일반, 강함, 따뜻, 동일>
    • h_{1, 2, 3} = <화창, 따뜻, 보통, ?, 따뜻, 동일>
      • h1에 x2를 반영하면, 바람 특징이 약함(x2), 강함(가설)으로 다름 -> 해당 특징은 ?가 된다.
    • h_{1, 2, 3, 4} = {화창, 따뜻, 보통, ?, 따듯, ?}
      • x4를 반영하면서 기상 변화 특징이 동일 + 변화 -> ?가 됨.
        • 어떤 문제가 존재할까?
        • 가능한 가설들이 너무 많아 정리 할수 없음.

버전 공간 version space

  • 너무 많은 가설이 존재할 수 있어, 하나의 가설로 모으기가 힘듬
  • 특정 가설을 찾기 보다는 범위에 속하는 것을 가설들을 찾아보자
  • 가능한 가설 집합 == 버전 공간 : 구간을 정해주자
    • 일반 구간 G : 버전 공간의 최대 일반화 가설 집합
      • 특정 구간 S : 버전 공간의 최대 특수화 가설 집합
      • 버전 공간에 속하는 가설 VS_{H, D}는 일반 구간 G와 특정 구간 S에 속하는 가설들을 갖는다.

후보자 제거 알고리즘 candidate elimination algorithm

  • 버전 공간을 만들기 위해서 가장 일반, 가장 특수한 가설들을 제거해 나가면서 특정 버전 공간을 만드는 알고리즘
  • 가장 특수한 가설들을 만들어 주자 -> ex S0 : <0, 0, 0, 0, 0, 0, 0> 무조건 운동 x
  • 가장 일반적인 가설 -> ex) G0 : 무조건 나가 운동
  • 데이터셋 D의 모든 인스턴스 x를 사용
    • x의 라벨 y가 참이라면
      • 인스턴스를 품을수 있을 만큼 특수화 된 가설 S를 일반화
    • 거짓 이라면
      • 일반 가설 G를 특수화.
        • 특정 특징이 가장 일반화, 특수화 된 경우가 동일하다면 더이상 특수, 일반화가 불가

이게 잘 동작하는가?

  • 후보자 제거 알고리즘으로 올바른 가설들을 구할수 있는가?

    • 수렴하는가? -> 가설을 구할수 있어야 한다.
    • 올바른가? -> 관측하여 얻은 가설은 참이어야 한다.

  • 다음의 가설이 주어진다면, 잘 동작한다고 할 수 있다.

    • 관측 오차와 관측 불일관성이 존재하지 않고,
    • 임의 오차가 존재하지 않고
    • 모든 관측 정보로 시스템을 예측할수 있는 경우

  • 하지만 위 가정을 할 수 있는 완벽한 세상은 존재하지 않는다.

    • 데이터 셋 D의 x인스턴스의 어느 특징에든 노이즈를 가지고 있고,
    • 노이즈로 인해 올바른 가설이 제거될수도 있어 올바르게 동작한다고 할 수 없다.

  • 이러한 규칙 기반 머신 러닝 기법의 한계로 노이즈에 강인한 결정 트리가 나옴

300x250
저작자표시

'인공지능' 카테고리의 다른 글

[인공지능및기계학습]02.4 엔트로피와 정보 이론  (0) 2021.01.14
[인공지능및기계학습]02.3 결정 트리 개요  (0) 2021.01.13
[인공지능및기계학습]01.동기부여 및 기초  (0) 2021.01.07
컴퓨터 비전 & 패턴 인식 - 32. 아웃라이어에 대처하는 기하 변환 방법  (0) 2020.12.16
컴퓨터 비전 & 패턴 인식 - 31. 기하 변환과 최소 제곱법  (0) 2020.12.16
728x90

이전 부터 인공 지능에 대해 무크 사이트에서 공개 강의로 올라와 있는건 알고 있었지만

그 동안 볼때마다 확률, 통계, 공업 수학 등 이론적 배경이 부족하다 보니 이해하는데 어려움이 많았었다.

그래서 전에는 포기하고 제대로 보지 않았는데

오늘 네이버 메일로 이 강의가 다시 와있더라

kaist.edwith.org/machinelearning1_17/lecture/40603/

그 동안 배경 이론들을 많이 연습했으니 이제 볼수 있을것 같아 한번 보았다.

머신 러닝 기법 응용사례로

스팸 메일 여부, 주가 예측, 헬기 제어 등을 보여주더라

머신러닝 분야

  • 지도 학습 : 인스턴스 별 결과, 라벨을 아는 경우 머신 러닝
  • 비 지도 학습 : 인스턴스 별 결과, 라벨이 주어지지 않는 경우의 머신 러닝
  • 강화 학습 : 목표가 있으나 어떻게 목표에 도달하는지에 대한 정보가 없는 경우의 머신러닝

지도 학습 supervised learning

  • 실제 결과를 알고 있는 문제를 학습하는 경우
  • 예시
    • 스팸 필터링
    • 자동 물품 카테고리 분류
  • 분류 classification와 회귀 regrssion
    • 참 거짓 맞추기 Hit or Miss : 양성, 음성 분류하기
    • 점수 매기기 Ranking : A+, B, C, F중 무엇을 받았을까?
    • 값 예측 value prediction : 물품의 가격 예측하기

비지도 학습 unsupervised learning

  • 결과를 주어지지 않고, 주어진 데이터만으로 학습하는 문제
  • 비지도 학습 예시
    • 군집 찾기 cluster
    • 숨겨진 인자(요소) latent factor 찾기
    • 그래프 구조 찾기
  • 클러스터, 필터링,
    • 텍스트 데이터로부터 주제 단어 찾기
    • 얼굴 데이터로부터 latent 중심 이미지 찾기
    • 궤적 뎅이터에서 노이즈 필터링 하기

압정 문제 Thumbtack Question

  • 압정을 던졌을 때 기울어져 있을까? 뒤집혀 있을까?
  • 동전은 앞뒷면이 동일하니 50:50이지만 압정은 다른 결과가 나올것임
  • 5번 던졌을때, 3번은 뒤집혀 있었고(핀이 위), 2번은 기울어 져있었(머리가 위)다고 하자.
    => 시행 결과 핀이 위일 확률은 3/5, 머리가 위일 확률을 2/5

이항 분포

  • 이산 확률 분포중 하나로 상호 배반 사건만 존재하는 시행들(베르누이 시행)으로 나타나는 확률 분포
  • 압정 던지기는 iid 라는 가정을 함. 독립적(independent)이고, 동일한(identically distributied) 확률 분포를 가짐.
  • 데이터 D = H, H, T, H, T로 주어질때,
    • n = 5
    • k = a_H - 3
    • p = theta(H가 나올 확률)
  • P(D | theta) = theta^(a_H) (1 - theta)^(a_T) : theta 가 주어졌을때, D가 관측될 확률
  • 이항 분포의 PMF : f(k; n, p) = P(K = k)=

최대 가능도 추정 Maximum Likelihood Estimation

  • P(D | theta) = theta^(a_H) (1 - theta)^(a_T)
  • 우리의 가정 : 압정 던지기 결과는 theta 확률의 이항 분포를 따른다.
  • 어떻게 theta를 설정할때 가장 이 데이터를 가장 잘 설명을 할수 있을까?
    • 관측 결과를 가장 잘 나타내는 분포를 찾아야 한다.
    • 최적의 theta를 구하여야 한다. 어떻게 theta를 구할까?
  • 최대 가능도 추정 : 관측된 데이터들의 확률을 최대화 하는 theta를 찾는 방법
    • hat{theta} = argmax_{theta} P(D|theta)
    • 위 압정 시행을 통해 추정한 hat{theta} = a_H/(a_t + a_H)

시행 횟수와 에러 구간

  • 추가적인 시행은 추정 오차를 줄여주게 된다.
  • 추정 모수 hat{theta}, 진짜 모수 theta^*라고 할때
  • Hoeffding의 부등식에 따르면 다음의 확률 상한을 얻을 수 있음.
    • 시행 횟수가 늘어날수록 실제 오차와 추정 오차 간격이 줄어듦.
    • P(|hat{theta} - theta^*| >= e) <= 2 e^{2Ne^2}
  • 이것은 PAC(Probably Approximate Correct) learning
    • 추정량 hat{theta}는 위 확률 범위와 오차 범위 내에서 올바름

베이즈와 사전 확률

  • 사전 정보를 파라미터 추정 과정에 반영 할수 있음(사전 확률)
  • 사전 정보를 가미한 추정량을 구하자
  • P(theta | D)Posterior = P(D|theta)Likelihood x P(theta)Prior/ P(D)Normalizing Constant
    • 이전에 P(D|theta)는 정의하였음.
    • P(D | theta) = theta^(a_H) (1 - theta)^(a_T)
  • 50:50이 사전 확률 P(theta)로 사용 될 수 있음.
  • 사전 확률과 데이터를 반영한 P(theta | D)를 구해보자

베이즈 관점에서 살펴보기

  • P(theta | D) 비례 P(D | theta) P(theta)
    • P(D | theta) = theta^(a_H) (1 - theta)^(a_T)
    • P(theta) = ????
    • 가능도 P(D | theta)가 이항분포를 이용하여 구한것 처럼 P(theta)도 확률 분포를 이용하여 구할 수 있다!!
  • 베타 분포로 사전 확률을 사용하자.
    • 베타 분포의 확률 밀도 함수 P(theta) (이항 분포에서 앞면, 뒷면 횟수로 가능도를 구한것 처럼, alpha와 beta가 필요)

  • 사후확률 P(theta | D)를 정리하면..
  • P(theta | D) 비례 P(D | theta) P(theta) 비례 theta^(a_H) (1 - theta)^(a_T) theta^{alpha -1} (1 - theta)^{beta -1} = theta^{a_h + alpha - 1} (1 - theta)^{a_t + beta - 1}

베타 분포로 사전 확률을 사용하자.

사후확률 최대화 MAP Maximum A Posterior

  • MLE에서는 가능도 P(D | theta)를 최대화 하는 추정량 theta를 구하였었다.
    • hat{theta} = argmax_{theta} P(D | theta)
    • hat{theta} = a_h/(a_h + a_t)
  • MAP는 가능도가 아닌 사후확률을 최대화 하는 추정량 theta를 구하는 방법
    • P(theta | D) 비례 thet^{a_h + alpha - 1} (1 - theta)^{a_t + beta - 1}
    • hat{theta} = (a_H + alpha - 1) / (a_h + alpha + a_t + beta - 2)
  • MLE에는 사전 확률을 반영할수 없으나 MAP는 사전확률을 반영할수 있게 된다!!
300x250
저작자표시

'인공지능' 카테고리의 다른 글

[인공지능및기계학습]02.3 결정 트리 개요  (0) 2021.01.13
[인공지능및기계학습]02.머신러닝의 기반들  (0) 2021.01.08
컴퓨터 비전 & 패턴 인식 - 32. 아웃라이어에 대처하는 기하 변환 방법  (0) 2020.12.16
컴퓨터 비전 & 패턴 인식 - 31. 기하 변환과 최소 제곱법  (0) 2020.12.16
컴퓨터 비전 & 패턴 인식 - 30. kd트리 기반 최근접 이웃 탐색  (0) 2020.12.16
728x90

아웃라이어의 영향을 제거하거나 약화시키는 방법이 필요

 

-> M 추정, 최소 제곱 중앙법이 있음

 

 

 

최소제곱법으로 구한 추정량을 아래와 같이 정의할때

 

 

M 추정 M estimator

 

m 추정을 활용한 식은 아래와 같음.

 

 

rho(r_i) = r_i^2이면 최소제곱법과 동일.

 

하지만 r_i가 일정 값 이상(오차가 크다면)이면 함수의 크기를 줄임.

 

이때 함수 rho()는 huber 함수로,

 

 

r이 임계값보다 작은 경우 2차 곡선 사용.(오차가 작으므로)

 

r이 임계값보다 큰경우 1차 곡선을 사용하여 오차의 영향력을 보다 줄임(오차가 크므로)

 

 

 

 

 

 

 

 

 

최소 제곱 중앙값 LMeds: Least median of Squared

 

최소 제곱 중앙값을 활용한 식은 아래와 같음.

 

 

n개의 특징점 중 중앙값을 취함.

 

중앙값인 매칭쌍의 오차를 최소로 하는 기하 변환 행렬 T의 매개변수들을 찾는 방법

 

 

 

 

붕괴점 breakdown point

 

더 이상 추정 알고리즘이 동작하지 않는 아웃라이어 비율.

 

최소제곱법은 붕괴점이 0%

 

최소제곱중앙값은 50%

 

 

 

 

 

 

 

 

RANSAC을 이용한 기하변환 추정

 

입력 : 대응쌍 집합 X, 반복 회수, 인라이어 판단 임계치 t, 인라이어 집합 크기 d, 적합오차 e

출력 : 기하 번환 행렬 T

 

 

Q = []

for i in range(k):
    X에서 임의의 대응쌍 3개 선택.
    세 대응쌍으로 최소제곱법으로 T_j 추정
    세 대응쌍은 인라이어로 판단
    
    m = X에서 세 대응쌍을 제외한 대응쌍 집합)
    for p in m:
        # T_j로 첫번째 대응쌍 요소를 변환시킨 p.1'와 p.2의 오차가 t보다 작은경우
        # 인라이어로 판단
        if  (p.2 - T_j*p.1) < e:
           p를 인라이어에 추가
           
    # 인라이어의 개수가 d이상이 되면
    if |inlier| >= d:
        인라이어 요소(대응쌍)들로 새 T_j 계산
    
    # 구한 T_j의 적합 오차가 e보다 작은경우 Q에 추가
    if T_j 적합 오차 < e:
        T_j를 Q에 추가
 
 Q에 있는 것들 중에서 가장 좋은 변환행렬 T를 선정

 

 

 

 

 

 

300x250
저작자표시

'인공지능' 카테고리의 다른 글

[인공지능및기계학습]02.머신러닝의 기반들  (0) 2021.01.08
[인공지능및기계학습]01.동기부여 및 기초  (0) 2021.01.07
컴퓨터 비전 & 패턴 인식 - 31. 기하 변환과 최소 제곱법  (0) 2020.12.16
컴퓨터 비전 & 패턴 인식 - 30. kd트리 기반 최근접 이웃 탐색  (0) 2020.12.16
컴퓨터 비전 & 패턴 인식 - 29. 이미지 매칭을 위한 거리 척도와 매칭 방법  (0) 2020.12.16
728x90

기하 정렬/기하 관계의 필요성

 

앞서 살펴본 매칭 과정은

 

지역 정보. 특징점의 기술자만을 사용하여 대응점들을 찾았다.

 

하지만 동일한 물체끼리는 기하 변환 관계를 가치는데, 이 기하 정렬 geometrical alignment조건 을 고려할 필요가 있음.

 

 

www.cc.gatech.edu/~hays/compvision/proj2/

 

 

 

 

기하 변환을 위한 최소 제곱 법

 

그동안 선형 모델을 구할때 최소 제곱법을 자주 사용했었는데,

 

컴퓨터 비전 문제에 최소 제곱법을 사용해보자.

 

위와 같은 두 영상에서 대응쌍 구했다고 하자

 

X = {(a1, b1), (a2, b2), . . ., (a_n, b_n)}

 

이 대응 쌍들은 기하 변환을 통해 얻었을탠대

 

회동, 이전, 크기 변환을 포함한 기하 변환 행렬 T로 나타내자

 

 

 

기하 변환 행렬 T로 a_i들 맵핑하여 b_i'를 얻을수 있게 된다.

 

 

 

 

실제 b_i와 a_i를 변환하여 얻은 b_i'사이에는 오차가 존재할텐대

 

이 오차를 최소화 하는 변환 행렬 T를 구하는게 목표가 되겠다.

(변환 행렬의 파라미터 6개를 구한다)

 

 

오차 E(T)를 기하 변환 행렬 T의 각 요소들로 편미분한 것을 0으로 하여 식을 얻고

 

행렬식을로 표현하면 아래와 같이 정리할 수 있다.

 

 

 

 

최소 제곱법의 한계

 

하지만 최소 제곱법은 오차가 정규 분포를 따르는 경우 정상적으로 동작한다.

 

그래서 아웃라이어의 영향을 크게 받는데,

 

아웃라이어를 제거하거나 이에 강인한 기하 변환 행렬을 구할 수 있는 방법이 필요하다.

 

https://slideplayer.com/slide/2342847/

 

 

 

 

 

 

 

 

 

 

 

300x250
저작자표시

'인공지능' 카테고리의 다른 글

[인공지능및기계학습]01.동기부여 및 기초  (0) 2021.01.07
컴퓨터 비전 & 패턴 인식 - 32. 아웃라이어에 대처하는 기하 변환 방법  (0) 2020.12.16
컴퓨터 비전 & 패턴 인식 - 30. kd트리 기반 최근접 이웃 탐색  (0) 2020.12.16
컴퓨터 비전 & 패턴 인식 - 29. 이미지 매칭을 위한 거리 척도와 매칭 방법  (0) 2020.12.16
컴퓨터 비전 & 패턴 인식 - 28. 중간  (0) 2020.12.16
728x90

나이브 최근접 이웃 방법, 단순 최근접 이웃 매칭

 

기본적인 매칭쌍 탐색 방법은 두 영상 사이 모든 점들을 매칭시켜 보는 것으로

 

1번 영상 특징이 m개, 2번 영상의 특징이 n개인 경우 mn번을 수행함.

 

 

대강 이런 식이 되지 않을까 싶다..

 

아래의 경우 최근접 이웃으로 했는데 조금 수정해서 최근접 거리 비율로 고칠수도 있겠다.

m = len(keypoints1)
n = len(keypoints2)


mlist = []

for i in range(m):
    shortest = inf
    idx_lst = []
    for j in range(n):
        dist = get_dist(keypoints1[i], keypoints2[j])
        if dist < smallest:
            shortest = dist
            if shortest < T:
                ids_lst.append(j)
     
     match = [i, min(idx_lst)]
     mlist.append(match)

 

하지만 이 방법은 가능한 모든 특징 쌍들에 대해 계산하므로 너무 오랜 시간이 걸리게 된다.

 

이 외 방법으로 이진 검색 트리를 개조한 kd 트리나 해싱을 이용할수 있겠다.

 

 

 

 

 

이진 검색 트리 binary search tree

 

이진 검색 트리는 특정 노드를 기준으로 왼쪽은 작은 값 오른쪽은 큰 값을 가지는 트리를 말한다.

 

아래의 그림을 보면 값이 8인 루트 노드를 기준으로 왼쪽으로는 8보다 작고, 우측으로는 8보다 큰 값을 노드들이 갖는다.

 

 

검색 키를 4라고 지정하면,

 

1. 8보다 4가 작으므로 왼쪽 노드, 노드 값이 다르므로 한번 더

 

2. 3보다 4가 크므로 우측 노드, 노드 값이 다르므로 한번 더 

 

3. 6보다 4가 작으므로 좌측 노드, 탐색 완료

 

이진 검색 트리를 이용해 3번만에 4를 찾을수 있었다.

 

 

https://en.wikipedia.org/wiki/Binary_search_tree

 

 

이를 슈도 코드로 나타내면 아래와 같이 정리할수 있겟다.

 

트리의 깊이는 log(n)이므로 빅오 표기법으로 O(log(n)) 시간에 검색 마침

 

t = binary_search(T, v):
if (t = Null):
    v가 존재하지 않음
else:
    키가 v인 노드 t를 반환

def binary_search(t, v):
    if t == Null:
        return Null
    if t.key == v:
        return t
    else:
        if (v < t.key): # 탐색 값, 키가 현재 노드의키보다 작으면 왼쪽 노드 탐색
            return binary_search(t.leftchild, v)
        else: # 아니면 우측 자식 노드 탐색
            return binary_search(t.rightchild, v)

 

 

 

 

 

 

 

 

 

 

 

 

 

빠른 특징 기술자 탐색을 위한 자료구조 - kd 트리

 

이진 트리 탐색 방법을 생각해보면

 

특징 벡터를 기반한 트리를 만들어 탐색함으로써

 

모든 특징벡터의 거리를 구해서 비교하는 기존 방법보다 빠르게 탐색할수 있겠다.

 

 

 

 

 

하지만 특징 벡터는 이진 트리처럼 1개의 값을 가지는게 아니라

 

SIFT 기술자는 128차원을 가지니 이에 맞는 트리 생성 알고리즘이 필요하다.

 

1975년 벤트리는 kd 트리를 제안함.

 

k dimension을 다루므로 kd 트리라 부르는것 같다.

 

 

kd 트리 분할 기준 2가지

 

1. 분할 축 선택

 

각 차원 분산 중 최대 분산을 가지는 차원 k를 분할 축으로 선정

 

2. 분할 기준 선정하기

 

차원 k 기준 정렬, 중앙값을 분할 기준으로 사용

 

 

X = [x_1, x_2, ...]

T = get_kdtree(X)

def get_kdtree(X):
    if X == Null:
        return Null
    else if X == 1: #단일 노드이면
        node.vector = X.m
        node.leftchild, node.rightchilde = Null
        return node
    
    else:
         k = 주어진 특징 벡터의 차원들 중에서 최대 분산을 갖는 차원
         X_sorted = sort(X, k)
         X_left, X_median, X_right = get_divided(X_sorted)
         
         node.dim = k
         node.vector = X_median
         node.leftchild = get_kdtree(X_left)
         node.rightchild = get_kdtree(X_right)
         return node

 

 

 

kd 트리를 이용한 최근접 이웃 탐색

 

새 특징 벡터 x가 주어질 때, 최근접 이웃을 탐색해보자

 

1. 루트 노드의 분할기준 차윈 k을 확인하다.

 

2. 입력 벡터의 k차원 값과 루트노드의 기준값을 비교하여 좌측 혹은 우측 자식 노드의 입력으로 보낸다.

 

위 1과 2를 단일 노드에 도착할때까지 판복한다.

 

 

이렇게 탐색한 단일 노드는 항상 최근접이라는 보장은 없음.

 

다른 트리 가지에 찾아낸 노드 보다 가까운 벡터가 존재할수 있기 때문

 

 

 

 

개선된 최근접 이웃 탐색

 

위 방법에서는 반대편 노드를 확인하지 못해, 분명하게 최근접인지 확인할수 없음.

 

현재까지 탐색한 노드들을 스택에 저장 -> 깊이 방향 탐색 수행

 

리프 노드 도착시 백트래킹 수행 -> 입력 벡터 x와 스택에서 꺼낸 노드 t의 특정 차원 오차가 최근접 거리보다 작은경우

 

=> 노드 t의 반대편에 더 가까운 노드가 존재할 가능성이 있음. 재귀 탐색 수행

 

 

이 방법은 노드가 많더라도 log(n)으로 빠른 탐색이 가능,

 

하지만 특징 벡터의 차원이 10차원 이상일 경우 모든 특징벡터를 수행하는것과 비슷해져 성능이 떨어짐.

 

#지나온 노드를 저장할 스택 생성
stack s = null;

# 현재 최근접 거리
current_best = inf
# 현재 최근접 노드
nearest = Null

search_kdtree(T, x)



def search_kdtree(T, x):
    t = T
    # 리프 노드가 아니면
    while is_leaf(t) == False:
        # 현재 차원기준, x가 현재노드보드 작다
        # 오른쪽 자식 노드는 스택에 대입
        # 왼쪽 자식노드는 t에 대입
        if x[t.dim] < t.vector[t.dim]
            s.push(t, "right")
            t = t.leftchild
        else
            s.push(t, "left")
            t=t.rightchild
    # 현재 노드 t와 x 거리 계산
    d = dist(x, t.vector)
    if d < current_best:
        current_best = d
        nearest = t
    
    #거쳐온 노드에 대해 최근접 가능성 여부 확인
    while s != null:
        t1, other_side = s.pop()
        #입력 벡터 x와 거쳐온 벡터 t1의 거리 계산
        d = dist(x, t1.vector)
        
        #거쳐왔던 벡터 t1이 최적이라면, 현재 최근접 거리와 벡터 변경
        if d < current_best
            current_best = d
            nearest = t1
        
        # (벡터 x의 어느 차원의 값 - t1의 어느 차원 값) < current_best
        # t1의 반대편 t_other에 보다 가까운 점이 존재할 가능성이 있음.
        if (x, t1.vector)의 분할 평면까지 거리 < current_best:
            t_other = t1의 other_side 자식 노드
            search_kdtree(t_other, x)

 

 

 

 

 

 

 

 

 

 

 

 

 

kd 트리를 이용한 근사 최근접 이웃 탐색

 

최근접 이웃이거나 가까운 이웃(근사 최근접 이웃 approximate nearest neighbor)을 찾는 방법

 

위 방법에서 스택 대신 우선 순위 큐인 힙을 사용

 

x로부터 거리가 우선순위로 이용됨.

 

-> 거쳐온 순서대로 백트래킹을 수행한 스택과 달리, 가장 거리가 가까운 노드부터 수행

 

추가로 try_allowed로 조사 횟수제한

 

 

#지나온 노드를 저장할 힙 생성
heap s = null;

# 현재 최근접 거리
current_best = inf
# 현재 최근접 노드
nearest = Null

# 비교 횟수
try = 0


search_kdtree(T, x)

def search_kdtree(T, x):
    t = T
    # 리프 노드가 아니면
    while is_leaf(t) == False:
        # 현재 차원기준, x가 현재노드보드 작다
        # 오른쪽 자식 노드는 스택에 대입
        # 왼쪽 자식노드는 t에 대입
        if x[t.dim] < t.vector[t.dim]
            s.push(t, "right")
            t = t.leftchild
        else
            s.push(t, "left")
            t=t.rightchild
    # 현재 노드 t와 x 거리 계산
    d = dist(x, t.vector)
    if d < current_best:
        current_best = d
        nearest = t
    
    try++
    #지정한 횟수만큼 우선순위 노드를 백트랙킹으로 탐색 후에는 종류
    if try > try_allowed:
        탐색 종료
    #거쳐온 노드에 대해 최근접 가능성 여부 확인
    while s != null:
        t1, other_side = s.pop()
        #입력 벡터 x와 거쳐온 벡터 t1의 거리 계산
        d = dist(x, t1.vector)
        
        #거쳐왔던 벡터 t1이 최적이라면, 현재 최근접 거리와 벡터 변경
        if d < current_best
            current_best = d
            nearest = t1
        
        # (벡터 x의 어느 차원의 값 - t1의 어느 차원 값) < current_best
        # t1의 반대편 t_other에 보다 가까운 점이 존재할 가능성이 있음.
        if (x, t1.vector)의 분할 평면까지 거리 < current_best:
            t_other = t1의 other_side 자식 노드
            search_kdtree(t_other, x)

 

 

300x250
저작자표시

'인공지능' 카테고리의 다른 글

컴퓨터 비전 & 패턴 인식 - 32. 아웃라이어에 대처하는 기하 변환 방법  (0) 2020.12.16
컴퓨터 비전 & 패턴 인식 - 31. 기하 변환과 최소 제곱법  (0) 2020.12.16
컴퓨터 비전 & 패턴 인식 - 29. 이미지 매칭을 위한 거리 척도와 매칭 방법  (0) 2020.12.16
컴퓨터 비전 & 패턴 인식 - 28. 중간  (0) 2020.12.16
컴퓨터 비전 & 패턴 인식 - 27. 대표적인 이진 기술자들  (0) 2020.12.15
728x90

아래와 같이 두 영상에 존재하는 동일한 건물의 특징점을 매칭하려면

 

두 특징점이 주어질때, 유사도나 거리 척도가 필요

 

 

http://vclab.kaist.ac.kr/cs484/hw4/index.html

 

 

 

유클리디안 거리 Euclidean Distance

 

유클리드 공간 상에서의 거리

 

위 사진에서 SIFT 기술자를 추출한다면 하나의 기술자 특징벡터는 128차원으로 이루어져 있을것임.

 

 

 

 

 

마할라노비스 거리 mahalanobis distance

 

점들의 분포 N(mu, sigma2)를 고려한 거리로

 

 

아래의 그림을 보면 분포 바깥 점이 평균과 더 가깝지만,

 

분포를 고려하면 멀리 위치한 분포 안의 점이 더 가까운것으로 판단함.

 

 

 

 

 

단순 매칭 전략 - 고정 임계값 사용

 

가장 단순한 매칭 방법은 고정 임계값 T을 사용하는 것으로

 

두 특징 벡터의 거리가 임계값보다 작은 경우 동일한 매칭 쌍으로 판단.

 

문제는 T가 너무 작은 경우 너무 적은 매칭 쌍만 생성됨. -> 매칭 쌍이지만 놓치는 경우 FN가 많이 발생

 

 

 

 

 

최근접 이웃 매칭 전략

 

주어진 특징 벡터와 가장 가까운 특징 벡터를 찾아 임계치보다 작으면 대응 쌍으로 판단.

 

1번 영상의 i번째 특징 벡터를 a_i,

 

2번 영상의 j번째 특징 벡터를 b_j라 할때

 

a_i와 가장 가까운 b_j를 탐색

 

d(a_i, b_j) < T인경우 매칭쌍

 

 

 

 

 

최근접 거리 비율 매칭

 

가장 가까운 특징벡터와의 거리와

 

두번째로 가장 가까운 특징벡터의 거리 비율이 임계치보다 작은 경우 매칭쌍으로 판단.

 

 

a_i와 가장 가까운 특징 벡터 b_j

 

두번째로 가까운 특징 벡터 b_k가 있을때

 

d(a_i, b_j)/d(a_i, b_k) < T 인 경우 대응쌍으로 판단

 

가장 좋은 성능을 보임

 

 

 

 

 

 

300x250
저작자표시

'인공지능' 카테고리의 다른 글

컴퓨터 비전 & 패턴 인식 - 31. 기하 변환과 최소 제곱법  (0) 2020.12.16
컴퓨터 비전 & 패턴 인식 - 30. kd트리 기반 최근접 이웃 탐색  (0) 2020.12.16
컴퓨터 비전 & 패턴 인식 - 28. 중간  (0) 2020.12.16
컴퓨터 비전 & 패턴 인식 - 27. 대표적인 이진 기술자들  (0) 2020.12.15
컴퓨터 비전 & 패턴 인식 - 26. 이진 기술자  (0) 2020.12.15

+ Recent posts

티스토리툴바