조건부 확률 conditional probability
- 정보가 주어졌을 떄 어떤 사건이 발생할 확률
주사위와 조건부 확률 - 상황
- 주사위 던질때 1의 눈이 나올 확률 1/6
- 짝수가 나올 확률 1/2
주사위와 조건부 확률
- 주시위가 3이하라는 정보가 주어짐. 짝수일 확률은 몇일까? 여전히 1/2?
- 위 경우 짝수인 경우는 세가지 중 하나
=> 3 이하라는 정보가 있을때, 짝수일 확률은 1/2(전체의 절반)가 아니라 1/3(3이하 수중 하나)
조건부 확률
- 주어진 정보로 사건 B가 발생하였다는 가정하에 사건 A가 발생할 확률
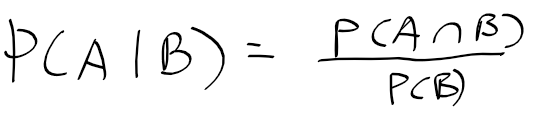
베이즈 정리
- 조건부 확률을 이용해 어느 사건의 발생 확률을 구하는데 사용되는 정리
베이즈 정리의 예시 - 공장
- 생산 라인 1(생산률 20%, 불량 비율 5%), 생산 라인 2(생산률 50%, 불량 비율 4%), 생산 라인3(생산률 30%,불량률 3%)
=> 문제 : 1) 전체 불량률은 몇일까? 2) 불량품이 첫 라인에서 만들어질 확률은?
전체 불량률
- 생산 라인 1 : 0.2 x 0.05 = 0.01
- 생산 라인 2 : 0.5 x 0.04 = 0.02
- 생산 라인 3 : 0.3 x 0.03 = 0.09
=> 전체 불량률 = 0.39
표본 공간 분할과 사건 A
- 표본 공간 S는 분할된 사건 B1, B2, B3, B4로 구성

사건 A가 주어졌을떄 조건부 확률
- 사건 A에 대한 정보가 주어진 경우, 사건 B_i에 대한 조건부 확률

베이즈 정리 bayes theorem
- 표본 공간을 B1 , ... Bk로 나눌 경우 사건 A와 조건부 확률 B_i는 아래와 같다.
=> 베이즈 정리 : 사전 확률과 분할 사건에 대한 사후확률을 구하는 아래의 식

베이즈 정리를 이용한 전체 불량률 구하기
- 전체 불량률 P(A)은 얼마나 되는가?
1. 사건 정의
- B1 : 제품이 생산 라인 1에서 만들어질 사건
- B2 : 생산 라인 2에서 만들어질 사건
- B3 : 생산 라인 3에서 만들어질 사건

2. 우도 likelihood 정리
- 각 라인에서 생산한 제품이 불량률일 확률

3. 베이즈 정리로 구한 전체 불량률
- 베이즈 정리로 사후확률과 사전 확률은 아래와 같이 정리할 수 있다.

- 지금 구하고자 하는것은 전체 불량률, 즉 사후확률 P(A)를 구하므로 다음과 같이 정리된다.

4. 베이즈 정리로 불량 제품을 뽑앗을때 1번 라인에서 생산한 제품일 확률

'수학 > 공업수학, 확률' 카테고리의 다른 글
| 확률 - 5. 이산 확률 분포 (0) | 2020.08.12 |
|---|---|
| 확률 - 4. 확률 분포 (0) | 2020.08.11 |
| 확률 - 2. 고전적 확률과 공리적 확률 (0) | 2020.08.07 |
| 확률 - 1. 확률 개요 (0) | 2020.08.07 |
| 통계 - 14. 최우추정법을 이용한 확률밀도함수 추정 (0) | 2020.08.04 |