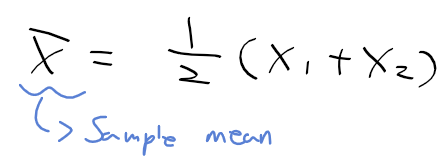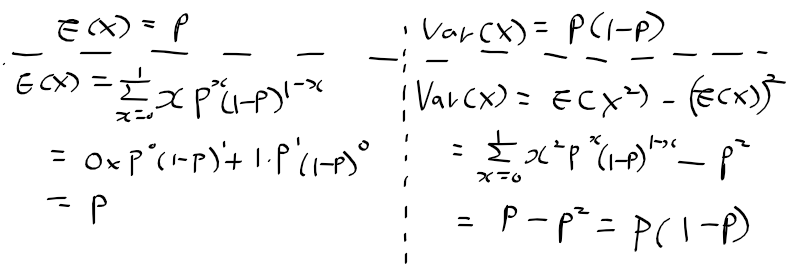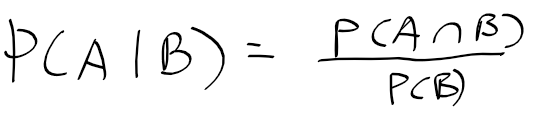일단 확률이란 과목 전반에 대해 간단히 살펴보았다.
이전에 확률 공부하면서
확률에는 이산 확률과 연속 확률이 있고
각 이산 확률 분포와 연속 확률 분포에는 어떠한 확률 분포들이 종류로 있는지는 대강 알고 잇엇다
하지만 후반부의 내용인
모집단, 모수, 표본집단(샘플), 통계량 등에 대한 개념은 대강 알기는 했었으나 다소 불명확하게 이해하고 있었다.
하지만 모집단 분포를 따라는 샘플 몇개를 추출해서 이 샘플의 평균과 분산을 통해 모집단을 추론해낸다.
라는 대략적인 과정을 이해할수 있었다.
또, 간단하게 시간의 변화에 대한 확률인 확률 과정과
임의의 난수를 생성시켜서 활용하는 몬테카를로 방법에 대해 간단히 살펴보았다.
이정도로만 살펴보고 마치기에는 확률론에 대해서
다소 부족한감은 있지만
대강 전체적인 범위와 무엇을 알아야하는지 정도는 파악되었고
중간에 애매했던 개념들을 이만큼 복습하였으면 충분할것 같다.
부족한 내용들은 다음에 다시 복습하는걸로 하고 확률 공부는 여기까지 하고자 한다.
다음으로 해야할 내용들은
대학 수학, 통계론, 제어 시스템, opencv-python 등이 있을것 같다.
추가적으로 가능하다면 공업수학 내용들을 한번 더 복습이 필요할것 같으나
지금 프로토타이핑을 공부하는 와중에 너무 많이 늘리기는 힘든 상황이다.
그나마 빨리 끝낼수 있는건 대학 수학정도 될것같긴한데,
하고싶을때 해야z
'수학 > 공업수학, 확률' 카테고리의 다른 글
| 확률 - 10. 몬테 카를로 방법 (0) | 2020.08.13 |
|---|---|
| 확률 - 9. 확률 과정 (0) | 2020.08.13 |
| 확률 - 8. 표본 분포 (0) | 2020.08.12 |
| 확률 - 7. 다변량 확률분포 (0) | 2020.08.12 |
| 확률 - 6. 연속 확률 분포 (0) | 2020.08.12 |