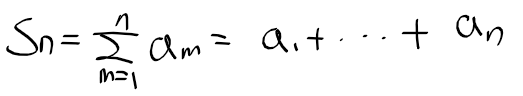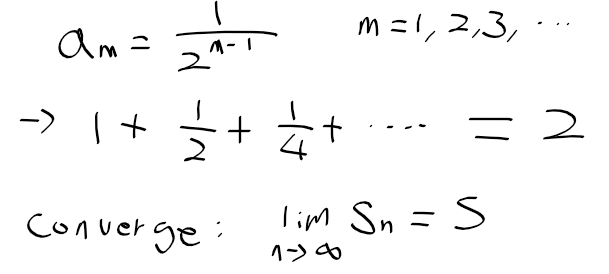집밖은 위험해

오늘 본 영상은 미래 설계에 대하여

요약하자면

아주 먼 미래는 어떻게 될지 모르니

가까운 1달이나 3~5년 이내 정도는 계획을 가지고 지내야 된다고 한다.

이 영상은 너무 짧아선지 큰 감흥은 없어서 

하나 더 봤다.

이번에는 하버드대 학생들에게 하는 얘기

정리하면

대학은 인생에서 4년 뿐인 아주 좋은 기회인데,

여기서 제대로 말하고, 듣고, 쓰는 방법을 배워야 한다.

집에서 놀고 먹는것보다 대학을 나오는게 좋고,

학생들이 가난한 이유는 젊기 때문. 부자는 나이많은 사람이 많다.

요즘 대학들은 취업교육만 하지 학생들에게 제대로 된걸 가르치지않는다.

오늘 본 영상들은

예쩐에 몇번 본적이 있는 영상들이어선지

처음 봤을때 만큼 감흥 있지는 않지만

그냥 보고 말았다.

그래도 어제 영상 보면서 생각정리한게 많이 도움이 되었는데

어떻게 해야할지 방향 못잡고, 무기력하게 있다가

그래도 글로 적으면서 생각도 정리하고 조금 구체화되니

막연함이 조금 줄어들고 목표가 조금씩 명확해지는 기분이 들더라

그런 이유로 오늘 일어나서 부터 조금씩 정리하다보니

생각보다 많이 올수 있었다.

조금더 공부할 수도 있지만

오늘 많이 했고, 보고서를 쓰느라 생각보다 시간이 늦었다.

보고서라 해도 내가 그날 한걸 그냥 생각나는데로 적는게 다다.

여기까지 하고 맘 편히 쉬어야지.

 매 주마다 공부한 내용을 보고서로 쓰고 있었는데

나중에 날라갈지도 모르니

매일 여기다 가도 같이 올리려고 한다.

학습 내용 및 느낀점

- 그 동안 SLAM 내용을 마친 이후에 결국 공업수학을 공부하게 되면서 지난 시간에는 공업 수학이라는 과목이 왜 필요한지 수학적 모델링과 이를 통해 만드는 방정식들의 종류 그리고 해가 어떤것들이 있는지 살펴보았습니다. 또, 가장 대표적인 1차 미분 방정식에서 해를 구하는 다양한 방법들과 현상들을 어떻게 수학적 모델링을 하여 해를 구하는 과정을 알아보았으나 대부분의 현상들은 비선형이므로 2차 이상으로 이루어진 미분방정식으로 나타낼 수 있다고하며, 이번 시간에는 2차 미분방정식과 이 이후의 내용들을 학습하였습니다.

- 지난 시간에 2차 미분 방정식이 어떤 형태로 되어있는지 보았으나 아직 2차 미분방정식의 해를 구하는 방법은 살펴보지 않았습니다. 대표적으로 상수 계수로 이루어진 미분 방정식에서는 미정 계수법이, 변수 계수로 이루어진 미방에서는 매개변수 변화법을 통해서 계수를 구할수 있는 것을 알게 되었습니다. 이러한 방법으로 미분방정식의 해를 구해보기도 하였으며, 다음으로 여러개의 선형 미분방정식들이 존재하는 선형 연립방정식에서 소거법을 이용함으로써 여러 종류의 미분방정식의 해를 구하는 방법들을 학습하였습니다.

- 1, 2차 미분 방정식에 대해서 살펴본 이후 매번 수학적 정리를 이용하는 해석적 방법을 통해 해를 구할수 있었습니다. 하지만 라플라스 변환을 통해 주파수 영역에서 다루면 조금 더 쉽게 해를 구할수 있었습니다. 라플라스 변환은 기존의 시간 영역에서 다루는 미분 방정식을 주파수 영역에서 다루는 대수 방정식으로 변환하는 것으로, 이공 분야에서의 문제들을 라플라스 변환으로 구한 대수 방정식을 연산하여 해를 구한후 역 라플라스 변환을 통해 시간 영역에 대한 함수로 다시 되돌린다고 합니다. 이러한 라플라스와 역 변환을 이용하여 조금 더 쉽게 해를 구할수 있는 방법을 알 수 있었습니다.

- 그 다음으로 무한 급수에 대해서 살펴보게 되었는데, 수능을 본 이후로 무한 급수에 대한 개념들을 많이 잊었었으나 다시 전반적으로 복습할수 있는 좋은 기회가 되었습니다. 무한 급수, 조화 급수 등의 급수들 뿐만아니라 무한 제곱 급수를 이용하여 이후에 자주 사용하게 되는 테일러 급수를 유도하는 과정에 대해서 알아보았으며, 테일러 급수와 유사하나 더 간단한 매클래인 급수를 유도하면서 다양한 급수들과 수렴의 개념에 대해서 정리하였습니다.

- 이제서야 제가 그동안 간단하게 배우고 싶던 수치 해석에 대해서 살펴보았는데, 공업수학의 일부분이다 보니 많은 부분들을 살펴본 것은 아니나 수치해석의 개념과 대표적인 수치해석 방법을 통해 근사해를 구하는 과정, 해석적 방법과 수치적 방법의 차이, 그리고 초기값 문제에서 해를 구하기 위한 오일러 방법, 테일러 방법, 룽게-쿠타 방법 등의 정의와 이를 통해 해를 구하는 과정에 대해서 이해할수 있었습니다.

- 오늘은 2차 미분방정식부터 수치해석까지 전반의 내용들을 살펴보았습니다. 아주 깊이 들어간 것은 아니나 이후 응용분야에서 사용하는 용어들을 이해할수 있는 정도로 최소한은 확인한 것 같습니다. 다음 시간에는 벡터와 행렬, 그리고 벡터의 미적분에 대해서 학습하여 마무리 하고자 합니다.

초기값 문제

- 미분방정식, 초기조건으로 구성

초기값 문제에 사용하는 다양한 수치적 해법

1. 오일러 방법 euler method

2. 테일러 방법 talyor method

3. 룽게-쿠타 방법 runge-kutta method

주어진 1계 초기값

오일러 방법

- x >= x0 일때, y(x)의 해를 구하기 위해 x의 구간을 h로 나누면

- 단순 오일러 방법 : x0에 대해서 y의 도함수를 구하고 일반화 시켜 해를 구하는 방법

테일러 방법

- 2항 테일러 방법 : y(x)의 테일러 급수에 x = x_{n+1}을 대입하여 아래의 식을 구하고, 앞의 두 항만 골라 구한 식

3. 룽게-쿠타 방법 runge-kutta 방법

- 테일러 방법에서 등간격 h를 사용하였고, f(x, y)를 계속 미분하였음.

- 룽게-쿠타 방법은 테일러 방법과 유사하나 f(x,y)에 따라 h를 적절히 바꾸고, f(x, y)를 여러번 미분할 필요가 없음

- 방법은 생략

문제를 해결하는 방법

1. 해석적 방법 anlaytic method

- 수학적 정의와 정리들을 이용하여 문제를 푸는 방법

2. 수치적 방법 numerical method

- 컴퓨터 연산을 통해 문제를 해결하는 방법

f(x) = 0을 만족하는 근 x를 찾기 위한 해석적 방법과 수치적 방법

1. 해석적 방법

- 1차 방정식 linear equation과 2차 방정식 quadratic equation만 구할 수 있음

2. 수치적 방법 - 이분법 bisection method

- 이분법 : 구간을 반복적으로 이분하여, 오차 범위 내의 근을 구하는 방법

- 아래의 함수 f(x) =0를 만족하는 근 x를 찾는다면

- f(x) = 0 해를 찾기 위한 이분법 의사 코드

해석적 방법과 수치적 방법의 특징

1. 해석적 방법

- 해를 구할수 있는 경우 true solution을 얻을 수 있다.

- 해를 찾을수 없거나 계산량이 너무 많을 수 있음.

2. 수치적 방법

- 컴퓨터로 풀수 있도록 문제를 수정해야함

- 근사해를 구함

- 대부분 문제에서 해를 얻을 수 있음

수치 해석 관련 용어

- 참해 true solution : 실제 정확한 해

- 근사해 approximate solution : 실제 해에 가깝도록 근사하여 구한 해.

- 절단오차 truncation error : 근사에 의해서 해에서 나타나는 오차

- 자리수 오차 roundoff error : 컴퓨터의 소수 표현에 의해 생기는 오차

- 전파 오차 propagation error : 반복 중 이전 오차가 다음으로 넘어가는 정도

무한등비급수 infinite geometric series

- 첫 항이 a, 공비가 r인 무한 급수

조화급수 harmonic series

- 다음의 무한급수를 조화급수라 부름

- 조화급수는 발산하는 대표적인 급수

교대급수 alternating series

교대 조화 급수 alternating harmonic series

거듭 제곱 급수 infinite power series

- 급수의 중심 x_0(center)에 거급제곱들의 합인 급수

테일러 급수 Taylor series

- 우선 거듭 제곱 함수의 도함수들을 구해보자

- 거듭 제곱 함수와 도함수들에 x = x_0를 대입하면 다음과 같이 정리할 수 있다.

- 이를 계수 a_m에 대해서 정리하면 다음과 같다.

테일러 급수 Taylor series

- 위 계수 a_m으로 거듭 제곱 급수를 정리하면 아래의 식 f(x)가 테일러 급수이다.

매클로린 급수 McLaurin series

- 테일러 급수의 x_0에 0을 대입하여 얻을 수 있는 급수

매클로린 금수의 예시

- 지수함수, 삼각함수, 로그 함수, 등비급수, 이항급수 등

오일러 공식

무한 급수가 필요한 이유

- 계수들이 변수인 미분 방정식은 보통 무한 급수로 해를 구함

* 예외 : 무한 급수 없이 해를 구할수 있는 변수 계수 미분 방정식 -> 코시 오일러 미분방정식

무한 수열 infinite sequence

- 항이 무한개가 존재하는 수열

무한 급수 infinite series

- 모든 항의 합

부분합 partial sum 

- n항까지의 합

수렴 converge과 발산diverge

- 수렴 : 다음의 수열의 무한 급수의 합이 2에 가까워지듯 무한 급수가 하나의 지점이 되는것

- 발산 : 무한 급수가 수렴하지 않고 무한대로 가는 것

1차 미분방정식으로 풀 수 있는 문제들

1. 집단의 개체수 증가 감소의 수학적 모델링

2. 가열 및 냉각 법칙을 이용한 수학적 모델링

3. 자유낙하운동

4. 로지스틱 미분방정식

5. 전기회로 등

2차 미분방정식으로 풀 수 있는 문제들

1. 질량-스프링-댐핑 시스템

2. RLC 회로

라플라스 변환 Laplace transform

- 적분의 한 종류로 상미분 방정식 Ordinary Differential Equation을 대수 방정식 Algebraic Equation으로 변환한다.

라플라스 변환을 하는 이유

- 현상을 수학적 모델링한 상미분 방정식을 라플라스 변환을 하여 대수 방정식을 만든 후, 대수 방정식의 해를 구하여 다시 역 라플라스 변환을 하면 상미분 방정식의 해를 얻을 수 있기 때문

라플라스 변환 

- 시간 t>=0 에서 정의됨. 여기서 t는 시간 영역(domain)이며 시간에 대한 함수 f(t)에 라플라스 변환을 수행

- 라플라스 변환을 통해 주파수 영역, 즉 s영역에 대한 함수 F(s)를 얻을 수 있음.

역 라플라스 변환 inverse laplace transform

- s영역의 함수를 다시 시간영역에 대한 함수로 변환

라플라스 변환의 선형성

- 적분과 마찬가지로 라플라스 변환도 선형성을 가짐

라플라스 변환 성질

1. 시간 이동

2. 주파수 이동

3. 미분

4. 적분

등은 생략

단위 계단 함수와 디렉 델타 함수

- 생략

라플라스 변환을 이용한 미분 방정식의 해 구하기

- 이전에 미분 방정식에서 해석적으로 구하던것보다 간단하게 풀 수 있음

연립 미분방정식 system of coupled differential equations

- 여러 미지함수가 있는 여러개(coupled)의 미분 방정식을 연립 미분방정식이라 함.

- 각 미분 방정식들이 선형인 경우와 비선형인 경우가 존재함.

선형 연립 미분 방정식

- 아래의 두 미분방정식에 함수 x(t)와 y(t)가 존재하며, 각 미분방정식들은 선형임

- 비선형인 경우 해석적(수학적 방법)으로 구할수 없음

선형 연립방정식 풀이 방법

- 대입법 subsitution method/소거법 elimination method라 부름

 -> 여러개의 함수들을 줄여 하나의 함수에 대한 미분방정식을 만듦

선형 연립미분방정식 풀이

매개변수 변화법 method of variation of parameters

- 미정 계수법 method of undetermined coefficients는 상수 계수의 비동차 미분방정식에서만 사용 가능

- 일반적인 비동차 미분방정식의 특수해는 매개변수 변화법으로 구함

=> 모든 비동차 미분방정식의 특수해를 구할 수 있음.

다음의 2차 비동차 선형 미분방정식 표준형이 주어질때

미정 계수법 method of undetermined coefficents

- 상수 계수 2차 비동차 선형 미분방정식이 주어질 때

- 비동차항의 형태에 따라 미정 계수 undetermined coefficients를 포함시키는 특수해를 가정

- 이 특수 해를 미분 방정식에 대입하여 계수 값을 구하는 방법

* 상수 계수 미분방정식에만 사용 가능

상수계수 비동차 선형 미분방정식

- g(x) != 0 일때

비동차항에서의 특수해 형태

미정 계수법 풀이 예시