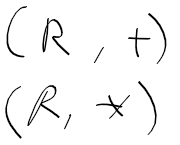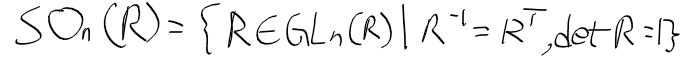집밖은 위험해

물체의 움직임 motion

- 3차원 공간상에서 움직임(모션)은 평행이동 translation과 회전 rotation으로 이루어짐.

- 회전은 각 축에 대해서 수행되며 3 x 3 행렬의 형태가 됨.

- 모든 회전을 나타내는 행렬 R은 하나의 군이라고도 할 수 있으며 SO_3(R)의 원소가 됨.

오일러각

- 각 축에 대한 \theta 만큼의 회전을 오일러 각이라고 함.

- 각 축에서의 오일러각 회전 행렬은 아래와 같음

2020-07-16

• 지난 시간에는 공업 수학을 마무리하고 앞으로 어떤 분야를 다뤄바야 할지 생각해보다가 원래 최적화를 공부하려던 걸 떠올리고, 이제서야 최적화를 공부하게 되었습니다. 최적화를 배우기에 우선 선형대수를 알아야 되고, 공업 수학에서 보았던 1변수, 다변수 함수에 대해서 다룰줄 알아야 했었습니다. 그러다 보니 이전에도 여러 차례 보았지만 오늘은 선형 대수 위주로 보면서 이전에 놓쳤던 부분이나 이해도가 부족한 부분들을 조금씩 채워나가는 방향으로 학습을 진행하였습니다.
• 가장 먼저 선형 대수에서 벡터와 행렬의 연산을 다루는데 항상 R이라고 하는 단어가 많이 햇갈렸었습니다. 이게 집합이라는 건 알고 있었는데 어떤거는 R의 3제곱, 어떤거는 그냥 R로 표기되어있고 함수 f와 같이 사용하니 함수의 집합이라는건지 그런 의미 등을 잘 모르고 있었는데, 이번 기회에 이런 개념들을 확립할수 있었습니다. 제가 궁금해했던 R의 n승은 벡터 공간으로 원소의 갯수가 n개인 벡터들의 집합이었고, 1차원 벡터 공간 집합은 R, 2차원 벡터 공간의 집합은 R의 2승, 3차원 벡터 공간의 집합은 R의 3승 식으로 이해할수 있게 되었습니다. 또한 선형 결합에 대해서 간단히 살펴보았는데, 이전에 공업 수학에서 살펴 본 덕에 선형 성을 가지고 있는 변수와 계수들의 조합인 걸 알고 있으니 간단히 넘어가고, 벡터에 있어서 선형 독립과 선형 종속을 그림과 수식 상에서 정리해보았습니다.
• 다음으로 선형대수에서 많이 보는 기저와 내적, 노름 등의 개념들을 살펴보았습니다. 기저가 basis로 뭔가의 기준이 된다는 의미는 알고 있었지만 정확하게 어떤 기준인지는 약간 불명확 했습니다. 하지만 이번에 반복을 하면서 선형 대수에 있어서의 생성이라는 개념과 함께 벡터 공간의 원소들을 생성하는 벡터를 기저라 함을 알 수 잇었고, 내적에 대해서 살펴보았는데 내적의 수식은 간단하지만 이 내적이 이후에 어떻게 활용되는지는 잘 몰랐습니다. 일단 내적은 두 벡터의 점곱으로 결국에는 스칼라 값이 결과로 나오지만 이후 내용들을 보면서 내적이 벡터의 거리를 구하는데 활용됨을 알수 있었습니다. 특히 한 벡터의 크기를 구할때 해당 백터의 내적에 루트를 씌워서 구하였으며, 두 벡터 사이의 거리를 두 벡터의 원소들의 차 제곱합에 루트를 씌운것으로 유클리디안 거리라고 부르는데 이 떄에도 내적의 개념이 활용되는 과정을 살펴보았습니다.
• 앞으로 벡터를 행렬들로 다루게 되는데, 다양한 행렬들을 전치, 대각, 단위, 교대, 역행렬등 다양한 행렬들을 살펴보았습니다. 그 중에서 이전에 로봇 공학을 공부할 때 확정 행렬이라는 용어가 종종 나왔었는데 정확히 이해하지 못하다 보니 확정 행렬에 대해서 자세히 살펴보았습니다. 확정 행렬은 대칭 행렬 A가 주어질때 n차원의 벡터 x와의 이차 형태의 행렬로 이 이차 형태가 0보다 큰 경우 양의 확정 행렬 그리고, 같거나 큰 경우에 양 세미 확정행렬로 종종 보는 개념이긴 하지만 이차 형태를 알고 나서 보니 조금은 이해할수 있었습니다. 또 행렬을 공부할때 역행렬을 자주 다루게 되는데, 역 행렬 이외에 특이 행렬과 비특이행렬이란 개념들을 잘 몰랐었습니다. 역행렬의 정의가 행렬 A가 주어질때 행렬 A와 곱연산을 하면 단위 행렬이 되는 행렬이지만 역행렬이 존재하는지 판별하는것이 중요 했었습니다. 그런데 이런 역행렬이 존재하는 행렬 A를 비특이행렬이라 하고, 역행렬이 존재하지 않는 행렬을 특이 행렬이라고 하는 부분들을 살펴보았고, 추가적으로 행렬 개념을 다룰때 랭크가 필요했는데, 저는 단순히 랭크가 행렬에서 행의 갯수 정도로 알고 있었지만 실제로는 선형 독립인 행 백터의 갯수로 조금 더 명확한 정의를 이해할 수 있었습니다.
• 수학에서 함수라는 용어는 자주 보았지만 f: X -> Y라는 개념은 잘 몰랐었습니다. 하지만 집합 X의 원소가 집합 Y의 원소에 대응하는 관계로 명확히 정의하고 넘어갔고, 벡터의 평행 이동을 수행하는 어파인 변환에 대해서 간단하게 살펴봤습니다. 이후 영상 처리나 제어 공학에서 가끔 봤던 개념인데 고유치와 고유 벡터에 대해서 알아봤습니다. 고유치와 고유벡터의 관계를 표현하는 공식과 푸는 과정은 봤지만 고유치의 의미에 대해서는 아직은 조금 부족하게 이해하고 있습니다.
• 하지만 앞서 살펴본 선형 독립과 고유 벡터의 개념을 이용해서 행렬 A와 이 행렬 A의 고유 벡터들 V가 주어질 때, AV로 부터 대각 요소를 구하는 과정을 정리해보았고, 여기서 A라는 행렬이 대칭 행렬인 경우 두 고유 벡터의 내적이 0으로 직교하는 사실을 증명하는 예제로 살펴보았습니다.
• 이후에는 그람-슈미트 직교화 과정이라는 방법을 통해서 n의 벡터 공간 상에서 선형 독립인 벡터로 서로 직교하는 다른 벡터들을 만드는 과정을 3차원 벡터 공간에서의 예시를 통해 정리 해보았고, 조금전에 살펴보았던 내적이란 걔념을 이용해서 유클리디안 거리구해 보았으며, 내적을 행렬로 바꾸어 대각화 요소를 포함하는 이차 형태로 변환하였습니다. 여기서 대각 행렬이 I라면 유클리디안 거리지만 대각 행렬이 데이터들의 공분산 이라면 마할라 노비스 거리로 정의되며, 데이터의 상관관계를 고려한 거리로 이 식을 유도하는 과정을 정리할수 있었습니다.
• 그 동안안 R이라고 하는 벡터 공간만을 보았지만, R이외에도 다양한 벡터 공간들이 존재하며 특정 이항 연산자에 대해 만족하는 집합 G를 군이라고 정의고, 이러한 군들이 어떤것들이 있는지 살펴보았습니다. 특히 군이라는 개념들은 논문에서 나오는걸 봤지만 선형 대수를 공부할때 군까지 가본적이 없다보니 이런 군과 관련된 표기를 봐도 이게 선형대수 용어인지, 기하학 용어인지 구분조차 하지도 못했었습니다. 적어도 이 군이 어떤것을 의미하는지 정도는 파악하는데 많은 도움이 되었습니다.

https://www.clien.net/service/board/lecture/15183818

내용과 댓글들이 많아 아직 다 읽어보지는 않았지만

공감되는 부분들이 많았다. 

글쓴분은 영어를 스킬 위주로만 접근하면 망한다고 하는데

특히 나의 경우가 그러했던것 같다.

내가 토익준비할때 당시 시중에서 가장 어렵다고하던 빨강이 1000제인가?

그 책을 사서

내가 모르는 단어와 틀린 문제 원인을 찾고 맞추는 식으로 연습을 하다보니

영어의 맥락을 파악하기 보다는

이전에 학습한 스킬 패턴데로 답을 찾아내고 있더라

그래서인지 배에서 실습 다닐때

토익 성적은 괜찬은데 왜 영어를 못하냐고 핀잔듣고는 했었다.

또한 수능 영어를 준비할때

내가 경험이 부족할것이라고 생각해서

계속 반복을 했지만

성적은 일정한 만큼만 오르고

더 이상은 오르지 않더라

이런 궁금증에 대해서

글쓴분과 다른 사람들의 얘기하는 과정을 보면

다양한 관점에서 어떻게 다뤄야될지 도움될것 같다.

군 이론 group theory

- 컴퓨터 비전과 컴퓨터 그래픽스에서 자주 등장하며, 다음과 같은 군들이 있다.

군 이란?

- 집합 G가 이항 연산자 *에 대해 다음 조건들을 만족하는 경우의 집합. 

 => (G, *)은 군 group이 됨.

1. 결합 법칙

2. 항등원, 역원의 존재

3. 아래와 같이 교환법칙이 성립하는 경우 -> (G, *)는 가환 군 commutative group

군의 종류

1. 가환군 commutative group

2. 비가환군

- 공간상 물체의 평행 이동을 의미하는 군

- 행렬식이 0이 아닌 행렬의 집합 : general linear group

- 위 집합의 부분군이며, 회전을 나타내는 집합

3차원 벡터 공간에서의 직교 행렬

- 직교행렬 orthogonal matrix : 다음의 경우를 만족하는 행렬

- 직교행렬의 모임은 아래와 같다.

직교 행렬의 성질

1. 정규 직교 행렬의 거리(노름)은 불변

 - 정규 직교 행렬 U와 벡터 x이 주어질때 노름을 구하면 다음과 같다.

2.  직교행렬 U의 열 벡터 U1, U2, U3는 3차원 벡터 공간의 정규 직교 기저 orthnormal basis

 -  O_3(R)은 직교군 orthogonal group

 - U가 O_3(R)의 원소라면, 정규직교 기저로 이루어진 직교행렬들은 다음과 같은것들이 존재함.

외적 outer product

- 두 벡터 x, y가 주어질때 외적은 아래와 같다.

- x간의 외적은 대칭 행렬이며, 양의 준확정행렬이 된다.

마할라노비스 거리

- 다음의 샘플 데이터들이 있을때

유클리디안 거리 euclidean distance

- 아래의 두 벡터 x, y가 주어질때 두 벡터 사이의 거리는 다음과 같으며, 이를 유클리디안 거리라 한다.

내적과 거리

- 거리는 벡터의 내적에서 나온 것임

내적의 행렬 표현

- 위에서 벡터 x와 y의 내적을 행렬로 바꾸면

양의 확정 행렬 positive definite matrix을 이용한 내적의 정의

- 위의 내적의 행렬 표현에서 단위 행렬 I 대신 양의 확정 행렬 A로 내적과 노름, 거리는 아래와 같다.

 => 단위 행렬 I로 내적을 정의한 경우 I-내적, 양의 확정행렬 A로 내적을 정의하면 A-내적이 된다.

그람-슈미트 직교화 과정 gram-schmidt orthogonalization process

- n 벡터 공간에서 선형 독립인 벡터 u1, ..., uk로 서로 직교인 벡터 v1, ..., vk를 만드는 과정.(k <= n)

3 벡터 공간에서 그람 슈미트 직교화 과정

- 다음과 같이 선형 독립인 3개의 벡터가 주어질때, 서로 직교인 벡터 u1, u2, u3을 구해보자

- v1 = u1으로 하고, v2는 u2에서 u1으로 투영한 벡터로 한다.

- v3은 u3을 v1, v2 평면에 사영한 벡터가 된다.

대각화 diagonalization

- 3 x 3 행렬과 선형 독립인 고유 벡터 3개가 주어질때

직교 고유벡터

- 대칭 행렬의 두 고유 벡터의 내적은 0으로 두 고유 벡터는 직교한다.

 => 직교 고유 벡터 orthogonal eigenvector

대칭 행렬의 직교 고유벡터 예시

고유치와 고유 벡터

- n차원에서 n차원으로 n x n 형태의 선형 변환 행렬 A가 주어질때, n차원 벡터 v사이 다음 관계가 성립할때

고유치와 고유 벡터 구하기 예시

함수 function

- f: X -> Y 집합 X의 원소이 집합 Y의 원소에 대응하는 관계

선형 변환 linear transformation

- m x n 행렬 A이 열벡터 x를 n차원 벡터 공간에서 m차원의 벡터 공간으로 선형 변환(차원 변환)시킨다.

어파인 변환 affine transform

- 직선의 평행 이동