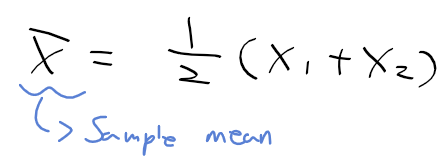집밖은 위험해

데이터 분석을 하려면 가장 먼저 할 일은?

-> 데이터 수집, 로딩

데이터 출력

- header =T 옵션 없으면 age, gender, group을 열이 아닌 1행으로 인식

변수 할당시 보기

- ctrl + 변수 명 클릭

head 함수

- 상위 6개 행 출력

- 데이터 상당히 많으므로 일부 볼떄 자주 사용

names 함수

- 열이름 확인하기

summary 함수

- 데이터 정리해서 출력

str 함수 (structure)

- 해당 데이터의 구조 출력

- 10개의 옵셔베이션, 3개의 바리어블

is.na 함수

- 결측치인지 반환

- is.na에 sum : true 가 1, false 는 0이며 true 가 없으므로 0이

colSums 함수

- 열 별로 sum 연산

- 아래의 예시는 각 열별 결측치 sum

read.csv()

- "tab" 쓰면 해당 wd의 파일 자동완성

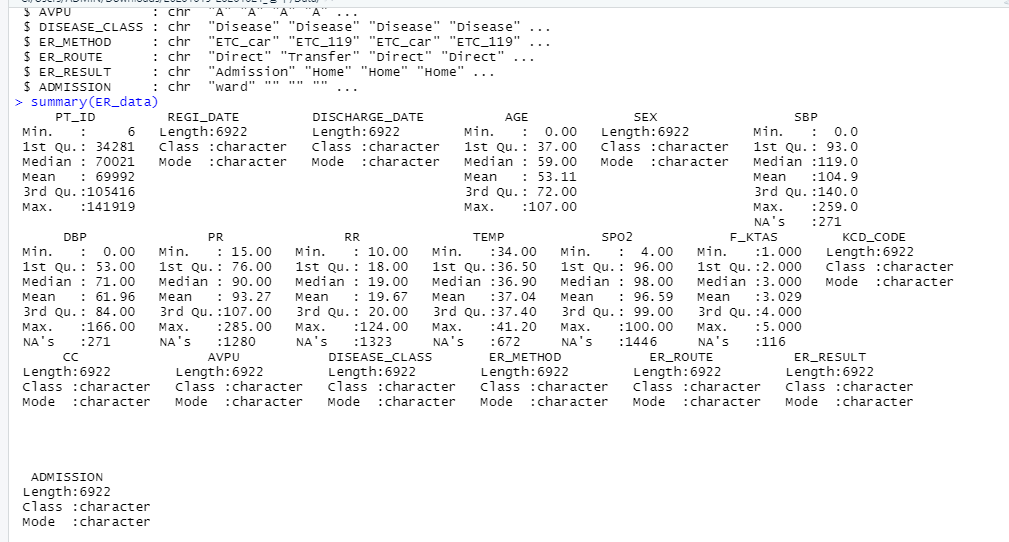
- 다음 예시는 6922 옵셔베이션에 20개 변수 가짐

csv 데이터 훑어보기

- str() : 구조 파악

- summary() : 기초 통계 빈도에 대한 내용 반환

- names : 변수명 확인

- is.na() : 결측값 확인

데이터 형태

- 데이터 프레임 : 엑셀과 같은 데이터

- 스칼라 : 1 x 1 형 데이터

- 벡터 : 1 x N 형 데이터

- matrix : M x N 형 데이터

* c() : concatenate의 약어로 스칼라 값들을 연결하여 벡터로 만듬

=> ex. c(1,2,3,4,10)

R 패키지

- CRAN The Comprehensive R Archive Network

- git

moonBook 설치 및 사용

- 성별을 기준으로 AGE, TEMP, AVPU 데이터 분석

유용한 R 패키지들

support.rstudio.com/hc/en-us/articles/201057987-Quick-list-of-useful-R-packages

- 배워야할 필수 패키지 4개

- Dplyr

- ggplot2

- ggvis

- caret

latex

- 논문쓸떄 많이 사용하며, html형태로 결과를 만들어줌

데이터 프레임 일부분 추출

- 데이터프레임명[행, 열]

데이터프레임 특정 변수 접근

- 데이터프레임명$변수

- age에서 1~4 추출

- age가 30보다 큰 추출 -> true false 반환

- age가 30보다 큰 age들 추출

- age가 30보다 큰 행 전체 출력

문제

# 나이가 30세보다 크고

# 성별이 M인 사람을 뽑자

통계를 배워야 하는 이유

- 무엇이 최선의 선택인가?

=> 데이터 주도 의사결정

통계학

- 실험으로 발견된 차이가 우연으로 예측된 차이보다 큰 것을 증명

- 통계 분석 : 그 결과가 우연인지 아닌지, 의미잇는 것은지 아닌지 분석하는 과정

통계학 배워서 할것들

- 데이터 시각화

- 통계적 시험

- 통계 개념 이해

- 여러 방법론 사용

고전과 현대 통계학

- 고전 통계학 : 수식과 알고리즘으로 소통

- 현대 통계학 : 데이터 기반

빅데이터 정의

- 4v도 있지만.

- 타임 스탬프(이 데이터가 언재)와 로케이션(어디서 생성되었는가)을 갖는 데이터

데이터 분석시 고려사항들

- 보정 adjust 

- 쪼개기 faceting

- 아웃라이어

- 결측치 

보정

- 해당 변수의 영향을 고려하는 것

ex) 폐암과 연관성이 높은 요소라고해서 무조건 암의 원인이라고 판단할수는 없음

보정의 예시

- 교회가 많아지면 범죄율도 증가한다

 => 인구가 늘면 교회도 늘고 범죄율도 증가

- 냉장고 보급률과 위암 환자에는 큰 관계가 있다

 => 사실 소득이 늘면서 냉장고 보급과 의료 서비스가 좋아짐. 위암 환자수가 증가

심슨의 역설

- 쪼개서 보아야 함. => 하위 그룹 분석

아웃라이어의 문제점

- 이상치로 인해 추정 값이 너무 심하게 변함

=> 평균, 회귀계수

결측치 NA Not Available

- 데이터에 결측치가 있는경우 분석되지 않을수도 있다.

- 데이터에 결측치가 포함된 경우 모든 통계값은 NA를 리턴하게되어 없애주도록 해야함

통계 분류

- 기술 통계 descriptive statistics : 수집한 데이터를 요약, 묘사

- 추론 통계 inference statistics : 모집단(알려고하는집단, 전체 집단)을 대표할수 있는 표본집합(모집단을 샘플링)으로 추론

기술 통계

- 수집된 데이터를 요약, 묘사(수치적, 시각화 등)

- 수치적 묘사 : centering 지표 ( 평균, 중앙값, 최빈값), spread 지표(분산, 표준편차), 웨도, 첨도 등

centering 지표

- 평균mean : 데이터의 합/ 데이터 갯수

- 중앙값 median : 데이터 정렬 후 가운데 값

- 절삭 평균 truncated mean : 양끝값을 제거 후 평균

=> 자료의 중심 측도 만으로 내용을 설명하기에는 부족함. spread 지표로 묘사

spread 지표

- 분산 variance : 평균에서 얼마나 멀어지는지. 데이터가 퍼진 정도

그 외 지표

- 왜도 skewness : 자료의 치우친 정도. 자료 대칭성 측도.

- 첨도 kurtosis : 얼마나 뾰족한가. 봉오리 높이 측도

추론 통계 inference statistics

- 수집 데이터로 추론, 예측하는 기법

- 전체 집단을 알수없기 때문 ->제한된 데이터 표본

- 모집단 population : 알고자 하는 전체 집단

- 표본집합 sampling : 모집단으로부터 추출한 집단

다양한 표본 추출 방법

- SRS Simple Random Sampling : 단순 랜덤 샘플링

- 층화

- 집락

- 계통

- PPS Proportional to Population Size : 모집단 크기에 비례하도록 추출

구간 추정

- 신뢰 구간

컴퓨터로 수학 문제를 풀때

대부분의 대학교에서는 MATLAB으로 가르치는데

매트랩이 그만큼 잘 되어있기는 하지만 학교 학생이 아닌 이상 라이센스 때문에 쓰기 힘들다

매트랩 말고 매트랩 비슷한 무료 소프트웨어가 있다고 하지만

제대로 찾아보지는 않았고

이전에 역도립진자를 파이썬으로 푼게 없는지 찾다보니

GEKKO란 라이브러리를 찾았다.

https://gekko.readthedocs.io/en/latest/overview.html

GEKKO는 비선형/대수 방정식을 최적화하여 해를 구하는 소프트웨어로

선형, 2차, 비선형 방정식 등 다양한 문제들을 풀어주고,

실시간 최적화, 동역학 시뮬레이션, 비선형 예측 제어 등의 모드가 제공된다고 한다.

GEKKO는 파이썬 래퍼로 벡엔드 단에서는 APMonitor가 실제 모델을 풀어준다.

다음 영상은 GEKKO 최적화 플레이리스트의 첫 영상으로

GEKKO가 무엇인지, 설치방법, hock & schittkowski 71번 문제를 푸는 과정을 보여주고 있다.

플레이리스트

GEKKO Optimization - YouTube

평균 변화율과 순간 변화율, 법선

- 평균 변화율 = 할선 scant line의 기울기 slope of secant

- 순간 변화율 = 접선 tangent line 의 기울기 slope of tangen

- 법선 normal line: 접선과 수직인 선

평균값 정리

- 함수 y = f(x)가 닫힌 구간 [a, b]에서 연속이고 (a, b)에서 미분 가능한 경우 아래의 식을 만족하는 c가 (a, b) 사이에 적어도 한개가 존재

$\frac{f(b) - f(a)} {b - a}$ = f'(c) 

극댓값, 극솟값, 극값

1. 극댓값 local maximum

 -열린구간 I에서 f(c)가 최대값인 경우 f(c)는 극댓값, x = c에서 f(x)는 극댓값 가짐

2. 극솟값 local maximum

 - 열린구간 I에서 f(c)가 최소값인 경우 f(c)는 극속값, x = c에서 f(x)는 극솟값이됨

3. 극값 local extrema

 - 극솟값 혹은 극댓값

=> 아래의 그림은 전역 극대점, 전역 극소점, 지역 극대점, 지역 극소점을 나타냄

최적화 문제

- 최대값이나 최소값을 구하는 문제

최소 자승법 least square method : LSM

- 에러 제곱 합 sum of squared error을 최소로하는 해를 구하는 방법

 => 점과 직선사이에 오차가 가장 작도록 하는 직선을 구할 시 사용

미소 증분과 선형 근사

- 미소 증분 $\Delta x$가 충분히 작다면 dx(미분)이 되며, 아래와 같이 정리 가능

  $\Delta_y$ = f(a + $\Delta_x$) - f(a) $\approx$ f'(a) $\Delta$ x

- a + $\Delta_x$ = x로 하면 다음과 같이 x = a에서의 직선의 방정식을 선형 근사하여 얻을 수 있다.

f(x) $\approx$ f'(a) (x - a) + f(a)

 => 직선이 아닌 n차에 대한 근사로 테일러 전개가 있음.

수치미분 numerical defferential

- 미분 공식으로 도함수를 얻을수 있으나, 미분 계수 근사값만으로도 충분할수도 있음.

- x = a에서의 미분 계수와 미소 증분이 충분히 작은 경우 평균 변화율(할선의 기울기)과 순간 변화율(점선의 기울기)은 비슷

순간 변화율(미분 계수) : f'(a) = $lim_{\Delta x -> 0} \frac{f(a + \Delta x)  - f(a) } {\Delta x}$

평균 변화율(미소 증분이 작은 경우) : f'(a) $\approx$ $\frac{f(a + \Delta x) - f(a)} {\Delta x}$

뉴턴 방법 netwon method

- 4차 방정식부터 근의 공식이 존재하지 않음

- n차 함수 f(x) = 0인 경우의 해를 어떻게 구할까?

1. x= a1에서 접선을 구함. 이 접선의 x 절편을 a2

   y - $f(a_1) = f'(a_1) (x - a_1)$

   $a_2$ = $a_1$ - $\frac{f(a_1)} {f'(a_1)}$

2. x = a2에서 접슨을 구함. 얻은 접선의 x절편 a3

....

=> f(x) $\approx$ 0인 x를 구하게 됨.

   $a_{n + 1}$ = $a_{n}$ - $\frac{f(a_n)} {f'(a_n)}$

$lim_{n -> \infty} a_n$ = $\alpha$

- f($\alpha$) = 0

- 아래는 뉴턴 방법으로 f(x) = 0이되는 x= $\alpha$를 뉴턴 방법으로 구하는 과정

경사법 gradient method

- 목적 함수, 비용 함수를 정의하여 이 비용이 최소(극소)가 되는 방향으로 내려가는 방법

- 보폭크기 $\alpha$만큼 경사 방향으로 내려감

일단 확률이란 과목 전반에 대해 간단히 살펴보았다.

이전에 확률 공부하면서

확률에는 이산 확률과 연속 확률이 있고

각 이산 확률 분포와 연속 확률 분포에는 어떠한 확률 분포들이 종류로 있는지는 대강 알고 잇엇다

하지만 후반부의 내용인

모집단, 모수, 표본집단(샘플), 통계량 등에 대한 개념은 대강 알기는 했었으나 다소 불명확하게 이해하고 있었다.

하지만 모집단 분포를 따라는 샘플 몇개를 추출해서 이 샘플의 평균과 분산을 통해 모집단을 추론해낸다.

라는 대략적인 과정을 이해할수 있었다.

또, 간단하게 시간의 변화에 대한 확률인 확률 과정과

임의의 난수를 생성시켜서 활용하는 몬테카를로 방법에 대해 간단히 살펴보았다.

이정도로만 살펴보고 마치기에는 확률론에 대해서

다소 부족한감은 있지만

대강 전체적인 범위와 무엇을 알아야하는지 정도는 파악되었고

중간에 애매했던 개념들을 이만큼 복습하였으면 충분할것 같다.

부족한 내용들은 다음에 다시 복습하는걸로 하고 확률 공부는 여기까지 하고자 한다.

다음으로 해야할 내용들은

대학 수학, 통계론, 제어 시스템, opencv-python 등이 있을것 같다.

추가적으로 가능하다면 공업수학 내용들을 한번 더 복습이 필요할것 같으나

지금 프로토타이핑을 공부하는 와중에 너무 많이 늘리기는 힘든 상황이다.

그나마 빨리 끝낼수 있는건 대학 수학정도 될것같긴한데,

하고싶을때 해야z

몬테카를로 방법 monte carlo method

- 특정 확률 분포로 난수를 수없이 생성

 -> 복잡한 문제의 해를 근사적으로 구하여 확률 문제 해결

- 표본 평균의 표본 수가 커지면 모집단 평균에 술며하는 성질 이용

몬테카를로 방법 예시

- 뷔퐁의 바늘 문제 : 수많은 평행선에 바늘던져, 평행선에 닿는 바늘 갯수에 대한 확률로 원주율 구함

- 폰 노이만의 실험

=> 확률분포 생성, 최적화 문제, 수학적 적분 등에서 많이 사용

확률 과정 stochastic process

- 시간의 흐름에 따라 관찰되는 확률 변수들의 모임

- 시간 t에서 관측값 X(t)

- 여러 시간 t1, t2 ...에서 확률 변수 모임 {X(t1), X(t2), . . } => 이 모임이 학률 과정

- ex. 주식 거래일의 종가, 일자별 날씨

마르코브 연쇄 markov chain

- 미래 상태는 과거가 아닌 현재 상태만의 영향을 받음

 => 확률과정이 무기억성을 가짐. 이를 마르코브 연쇄

확률과정과 정상 stationary 성질

1. 손자 수(X2)가 3명에서 증손자 수(X3)가 5명으로 늘어날 확률과

2. 10대 후손의 수 (X10) 3에서 11대 후손의 수 (X11)가 5명으로 변화할 확률은 같음

- 단계 n 상태 i에서 다음 단계에서 상태 j로 변화될 확률이 n에 의존하지 않는경우

 * 위 예시에선 2단계 상태 3에서 3단계 상태 5(1), 10단계 상태 3에서 11단계 상태 5로 변화

 => 확률 가정이 정상 성질을 가짐

전이 확률 transition probability

- 위 예시를 보면 상태 i에서 상태 j로 변화시 현재 단계 n과는 상관 없음.

- 이 확률을 i와 j만으로 나타낼 수 있음

- 상태 i에서 j로의 전이확률은 아래와 같음.

전이 확률 행렬 transition probability matrix

- 상태 i에서 상태 j로 변화할 확률을 (i + 1)번째 행, (j + 1)번쨰 열의 원소로 나타낸 행렬 P

 * (i + 1)인 이유는 상태가 0인 경우도 고려하기 때문

모집단 population

- 관심의 대상 전체

표본 sample

- 모집단의 일부분

모수 parameeter

- 모집단은 특정 분포를 따름

- 모집단의 특성을 나타내는 값(모집단이 변경되지 않는 이상 상수)

통계값

- 표본으로부터 얻은 값

 * ex. 임의로 선정한 1000가구의 평균 지출이 100만원인 => 100만원이 통계값

통계량 statistic

- 통계 값을 구하기 위한 수식

- 대표적인 통계량으로 표본 평균

표본 평균 구하기

- 확률 변수 X1, ..., Xn가 평균 mu, 분산 sigma^2인 모집단에서 추출된 경우

- 모집단의 평균 mu를 추정 inference 하기위한 표본 평균은 아래와 같음

주사위에 대한 확률 분포와 모수 구하기

- 주사위는 1 ~ 6까지 확률 변수값을 가지는 이산 균일 확률 분포를 따름

 => 모집단의 평균과 분산은 다음과 같이 구함

표본 크기가 2인 경우 주사위 표본 평균 구하기

- 이번에는 확률 변수 X1, X2가 주어질때 표본 평균을 구하면 다음과 같이 정의함

- X1과 X2가 아래와 같이 주어질때 표본 평균 bar{X}는 아래와 같다.

표본의 크기가 2인 표본 평균의 확률분포표

- 주사위를 두번 던질때 얻을수 있는(X1, X2의 조합) 표본 평균에 대한 확률 분포표는 아래와 같다.

표본의 크기가 2인 표본의 통계값

- 위 표본 평균에 대한 확률 분포가 주어질때 기대값과 분산은 아래와 같다.

=> 모 평균과 표본 평균은 7/2로 동일하나 표본 분산은 모 분산의 1/2가 됨.

표본 크기가 n인 표본 평균 bar{X}의 기댓값과 평균

- 다음과 같이 n개의 표본들이 주어질 때

- 이들을 샘플링하여 뽑은경우 표본 평균 bar{X}의 기댓값과 평균은 아래와 같다.

 => 1. 모 평균과 표본 평균은 동일

      2. 표본 분산은 모 분산/n

대수의 법칙

- 표분의 수가 커지면 표본 평균 bar{X}는 모 평균 mu에 수렴

모집단이 정규분포일때 표본 평균 분포

- 표본 평균은 모집단을 추정하는데 사용되므로 매우 중요

- 모집단이 정규 분포를 따르면 -> 표본 평균도 정규 분포를 따름

중심 극한 정리 central limit theorem

- 모집단이 정규 분포가 아니어도 표본 n이 충분히 크면 표본 평균은 정규 분포에 근사

자료 분석의 주요 관심사

- 두 변수 사이의 관련성

 * ex. 광고비와 순익의 연관성

결합 분포 joint distribution

- 2개 이상의 확률 변수들을 같이 고려한 확률 분포

 * ex. 키에 대한 확률 변수 X와 몸무게에 대한 확률 변수 Y => 키가 180cm 이상이고, 몸무게가 80kg 이상일 확률

다변량 확률 분포 multivariate distriubiton

- 여러 확률 변수들의 결합분포

이변량 확률 분포 bivariate distribution

- 두 확률 변수의 결합 분포

결합 확률 분포의 기대값, 공분산, 상관계수

1. 기댓값 expectation

- 이산/연속 확률 변수가 주어질때 결합확률질량/밀도 함수에 대한 기댓값은 아래와 같다.

2. 공분산 covariance

- 두 변수간의 관계를 나타내는값

3. 상관 관계 correlation

- 공분산은 각 확률 변수의 단위에 의해 정해짐

 => 각 변수의 표준편차를 나누어 표준화한 상관계수(rho)로 상관관계를 알 수있음

- 아래는 상관 계수의 식

조건부 확률 분포 conditional probabilistic distribution

- 조건부 분포 : 두 확률 변수 (X, Y) 중 Y의 값이 주어질때 X의 확률 분포

 * ex. X는 키, Y는 몸무게라고 할때, 몸무게가 80인 경우 키에 대한 확률 분포

- 두 확률 변수 X, Y가 주어질때 조건부 확률 분포는 다음과 같이 정의 가능

이변량 정규분포 bivariate normal distribution

- 정규분포를 2개의 변수에 대해 결합 분포로 확장한 것

 * ex. 키와 몸무게에 대한 확률 변수를 이변량 정규분포로 표현 가능

- 다음의 경우 두 확률 변수 X1과 X2에 대한 이변량 정규분포를 정리함

다변량 정규분포 multivariate normal distribution

- 이변량 정규분포와 마찬가지로 벡터와 행렬로 간편하게 표현 가능함

- p개의 확률 변수 X1, ..., Xp가 다변량 정규분포를 따르는경우 X1, .., Xp의 결합 확률 밀도함수는 다음과같음

 * 행렬식 determinant : 행렬의 역행렬이 존재하는지 판별하는 식

- 확률 변수 X가 다변량 정규분포를 따를때 다음과 같이 정리할 수 있다.

연속 확률 분포 continuous probability distribution

- 확률 변수가 연속(셀수 없는)인 경우에 대한 확률 분포

- 예시 : 균등 분포, 지수분포, 정규분포 등

연속 균등(균일) 분포 continuous uniform distribution

- 구간 [a, b]에 균일하게 분포된 확률 분포

- 균일 분포의 확률 밀도 함수와 표기를 다음과 같이 한다.

지수 분포 exponential distribution

- 사건이 독립일때, 일정 시간 동안 발생한 횟수가 포아송 분포를 따른다면, 다음 사건 발생까지 대기시간은 지수 분포를 따름

- 제품 수명에 대한 확률 분포로 자주 사용

  ex) 평균 수명이 1000시간인 부품이 있을때, 1000시간 이전에 고장날 확률은?

- 지수 분포의 확률 밀도 함수

- 지수 분포 예시 그림

정규 분포 normal distribution

- 평균점을 중심으로 좌우 대칭이며 종 모양의 확률 분포. 널리 사용됨

- 에시 : 학생들의 성적 분포, 남성의 콜레스테롤 수치 분포 등

- 정규분포는 다음과 같이 확률 밀도 함수와 표기를 한다.

- 정규 분포의 확률 밀도 함수