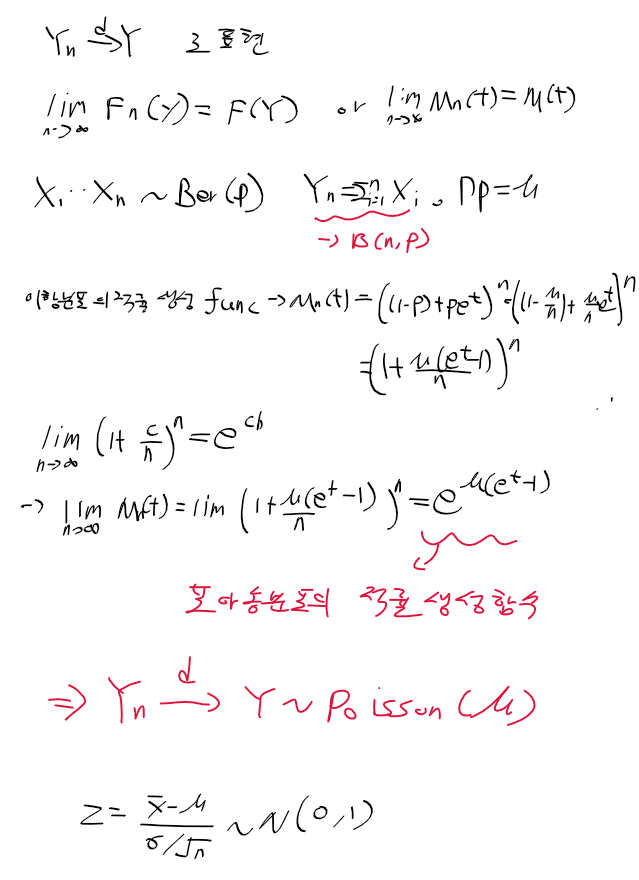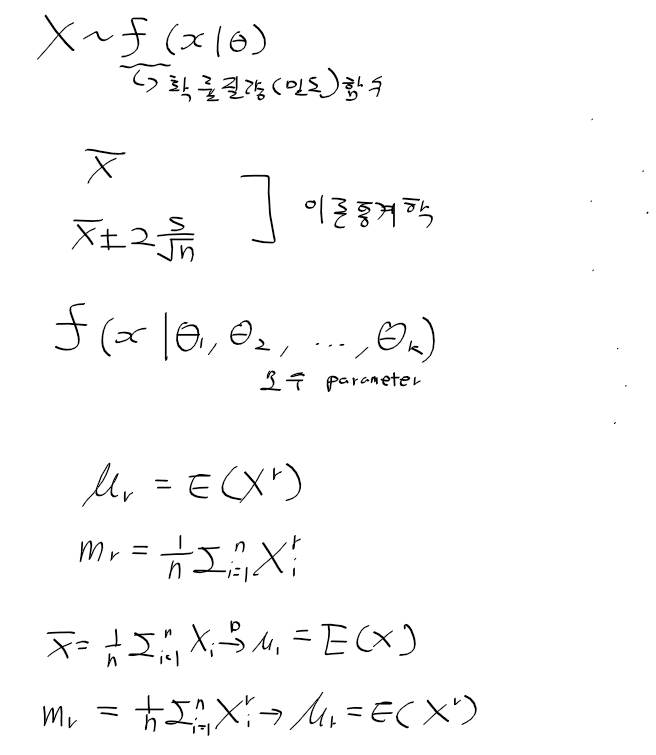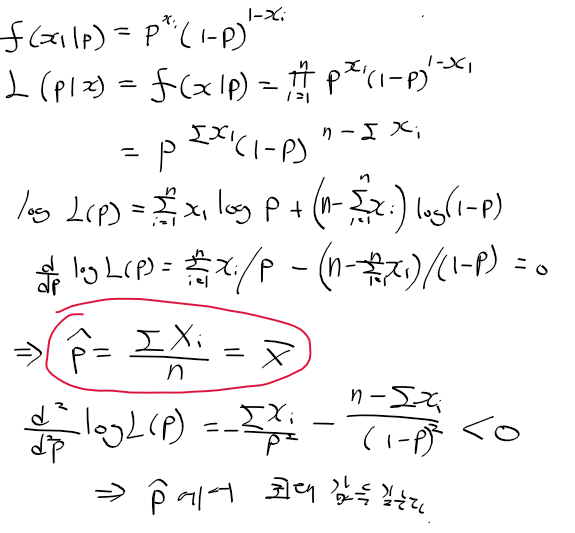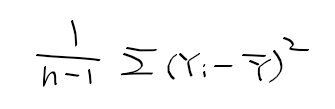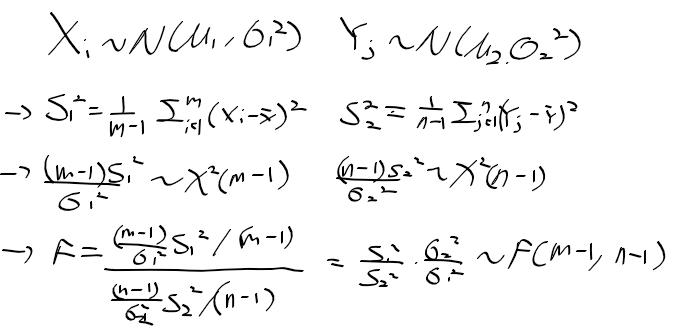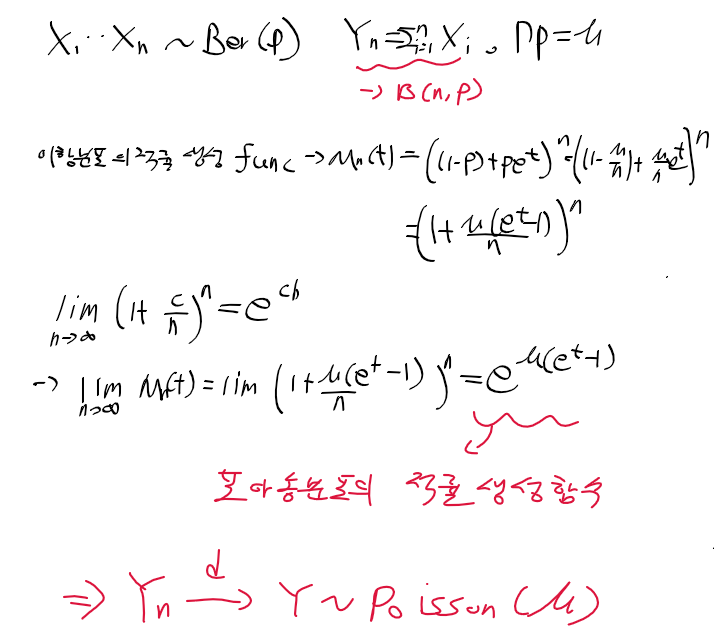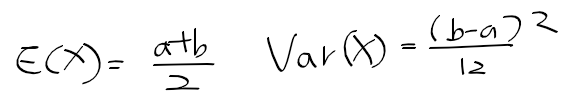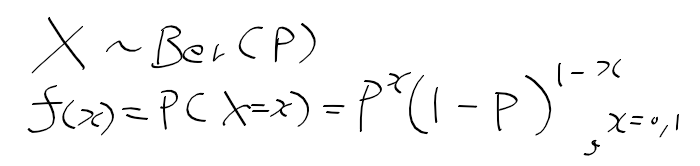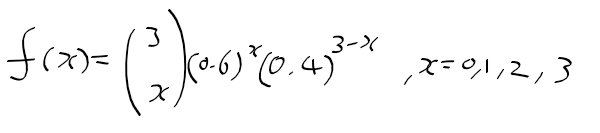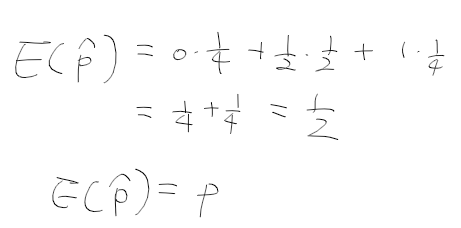집밖은 위험해

적률 추정량

최대 가능도 추정량

어떤 추정량이 좋은 추정량인가?

=> 불편 추정량, 추정량 효율성, 일치추정량, 평균제곱오차를 보자

추정량 estimator

- 모수를 추정하는데 사용되는 통계량 (표본의 함수, 표본평균/표본분산)

추정값 estimate

- 데이터에 근거한 추정량 값

좋은 추정량

- 추정량의 값이 모수와 항상 일치

- 추정량 선택 기준 : 불편성, 효율성, 일치성

추정량의 성질

- 불편성 : 평균하면 모수가 되는가

 => 불편 추정량 unbiased  estimator : 불편성을 가진 통계량

- 효율성 : 얼마나 밀집되어있는가

- 일치성 : 수렴한느가

불편향추정량 unbiased estimator

- 통계량 T가 다음을 만족하면 T는 불편 추정량

 => 불편향 추정량 : E(T) = theta

 => 불편향 추정량의 기대값은 모수가 됨.

편향 추정량 biased estimator

- 불편향 추정량이 되지 못하는 추정량

 => 편의 : bias(T) = E(T) - theta

불편향추정량 예제

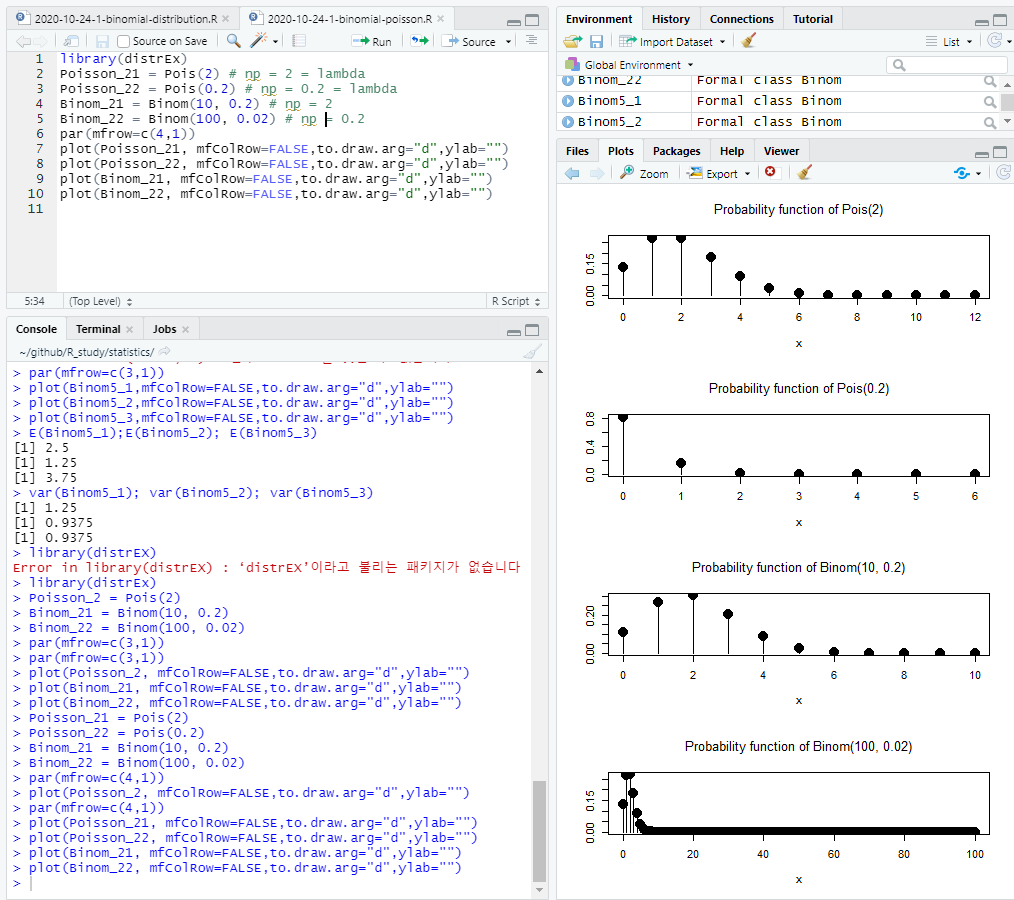
- X1, ..., Xn ~ Poisson(lambda)를 따르는 확률표본인 경우

- T1 = bar{X}이 불편추정량임을 증명

=> E(T1) = E(bar{X}) = lambda로 모수임을 증명함

편향 추정량 예제

- 다음 추정량의 편향을 구하라

효율성 efficiency

- 분산의 역수

- 불편 추정량 hat{theta}의 효율성

효율성 예제

- X1, ..., Xn ~ N(mu, sigma^2)을 따르는 확률 표본

- S2과 hat sigma2의 효율성을 구하라

- 

상대 효율성 relative efficienty

- 하나의 모수를 추정하는 2개의 불편 추정량이 있다면, 그 성능은 효율성으로 비교

- 모수 theta에 대해 불편추정량 T1, T2가 있을떄 T1에 대한 T2의 상대효율성

평균제곱오차의 필요성

- 불편 추정량과 편의 추정량 비교를 하기 위해 아까 본 예제를 다시보면

- 편향성과 효율성을 동시에 고려해야하며 기준 필요

=> MSE

평균제곱오차 Mean Sqaure Error, MSE

- 추정량 T와 모수 theta간 거리 제곱의 평균 측정값

- 통계량 T가 추정 통계량인 경우 T에 대한 평균제곱 오차는 다음과 같다.

평균 제곱 오차의 정리

- 통계량 T에 대한 평균 제곱 오차를 편향과 분산으로 나누면 다음과 같다.

평균 제곱오차 예제

- X1, .., Xn이 N(mu, sigma2)를 따르는 확률 표본인경우 추정량의 효율성과 평균제곱오차를 구해보자

- S2의 효율성과 평균 제곱오차

- sigma2 추정량의 효율성과 평균제곱오차를 구해보자

점추정 열심히 정리했는데 잘못 저장해서 날려먹엇다 ..

그냥 필기한거 복붙

적률 추정법

정규분포 적률 추정량 구하기

가능도 함수와 최대가능도함수로 최대 가능도추정량 구하기

최대가능도법으로 모수 p 추정하기

베르누이분포 최대가능도 구하기

정규분포 최대가능도 구하기

단순 선형 회귀 모델 simple linear regression model

- 회귀계수 beta0는 절편 intercept, beta1은 기울기 slope, 오차 epsilion ~ N(0, sigma^2)

단순 선형 회귀 모델 예제 - 회귀계수 beta0, beta1의 최대가능도추정량을 구하자

R 실습

1. 베르누이 분포 최대 가능도 함수로 확률 구하기

2. 정규분포 최대 가능도 함수

표본으로 추정한 모수(평균 키와 분산)

  1. 최대 가능도 함수로 모수 추정

  2. 가능도 함수로 데이터 만들고 plot

3. 단순 선형회귀 모델 beta0, beta1, sigma^2 최대 가능도 추정량 구하기

통계량들의 차 비에 대한 분포

극한 분포 - n이 커질떄 어떻게 수렴하는지

표본 평균의 차에 대한 분포

- 다음과 같은 표본이 주어질떄

- 표본 평균은

- 표본 평균의 차를 적률 생성 함수로 구할 수 있음

- sigma1과 sigma2가 동일하다고 가정하면 다음과 같이 표준화하면 표준 정규분포를 따르게됨

공통 분산

- 각각의 분산들을 추정할때 다음과 같이 계산

- X와 Y를 합한 공통 분산을 구하고, 이에 대한 카이제곱 분포는 m+n -2 자유도를 따름

표본 평균의 차에 대한 분포

- 두 집단 모분산을 모르지만 같다고 가정시, m+n - 2의 자유도를 같는 T분포를 따른다

표본 분산 비교

- 표본 분산의 경우 차 보다는 나누어서 주로 비교

F 분포

- 표본 분산비 : 카이제곱 통계령의 비 -> F분포로 표현됨. 분산분석법에 이용됨

- Fisher를 기르기위해 F분포라 명명

표본 분산의 비교

극한분포

- 표본수가 무한대가 될떄 어떻게 되는지

확률적 수렴

- 모집단이 N(mu, sigma^2)을 따르면, 표본 평균은 N(mu, sigma^2/n)을 따름

- n이 무한이 되면 표본 평균 bar{X}는 mu에 근접(약대수의법칙)

마르코브 부등식

- 약대수 법칙을 증명하기 위해 필요

- 확률변수 X가 주어지고 u(X)가 양의 함수일때 epsilon > 0에 대해 다음이 성립

약대수의 법칙

- X1, ... Xn 이 주어질떄 E(Xi) = mu, 분산 Var(Xi)= sigma^2인 모집단에서 확률 표본일때

- 표본평균 bar{Xn}은 상수 mu에 확률적으로 수렴

예제

- 표본 분산이 확률적으로 모분산에 수렴함을 증명하라

분포로 수렴

- 확률 변수가 하나의 값이 아닌 어떠한 분포로 수렴할수 있음

- 분포의 수렴을 알려면 CDF나 적률생성함수 사용

- 여기서 각 Yi의 누적 분포 함수 Fn(y)에서 n이 무한이 커진 F(y)를 극한 누적 분포 함수 limiting distribution이라 부름.

분포 정리 

- 베르누이 분포 : 베르누이 시행에 대한 분포

- 이항 분포 : 베르누이 시행을 n번 한 경우에 대한 분포

- 포아송 분포 : n이 충분히 크고, p가 작고, np가 lambda를 따르는 분포로 사건 발생 횟수에 간한 분포

- 지수분포 : 포아송 분포의 특수한 경우로 사건이 처음 발생할때까지 수명에 관한 분포

- 감마 분포 : gamma 번째 발생할 확률에 대한 분포

- t 분포 : 모분산을 모를때, 표본 분산의 분산을 구하기 위한 분포

- 카이제곱 분포 :  감마분포의 특수한 경우, t분포와 마찬가지로 통계량 추정을 위해 사용

분포 수렴 예제 - n이 무한이 커질때 이항분포가 포아송 분포를 따름을 증명

표본 평균의 분포

1. Xi가 정규분포를 따르는 경우

2. 정규 분포를 아니더라도. n이 무한이 커지면 정규분포로 수렴하게 된다.

R 실습

1. 정규 분포와 정규분포의 합 분포

2. 이항 분포 합의 분포 , 포아송 분포의 합의 분포, 정규분포 합의 분포, 정규분포 평균의 분포

그동안 계속 모집단에 대한 분포들을 연습했는데

모집단에서 추출한것이 표본이고

표본 수가 많으면 정규분포의 형태를 따르는 다나, 표본 평균의 평균/분산 까지는 이해가 되지만

표분 분산의 평균, 분산부터는 햇갈리기 시작한다 그래서 

다시 표본 분포에 대해서 살펴보고자 한다

앞서 살펴보니 이 파트에서는

확률 표본을 구성하는 확률 변수. 합의 분포와 변수 변환법으로 확률 변수함수의 분포를 본다고 한다.

내가아는 용어

* 확률 변수 : 표본 공간을 수로 만들어주는 함수  였엇지..

* 통계량 : 평균, 분산 등.

그 다음에는 확률 표본의 통계량인 표본 평균, 표본 분산과 관련된 분포 등에 대해서 다시 보자.

다시 용어정리

- 확률 표본 : 모집단에서 독립적으로 추출한 표본

- 통계량 : 모수 추정에 적합한 확률 표본들의 함수

   ex. 표본 평균, 표본 분산

- 표본 분포 : 통계량의 확률 분포

 ex. 표본 평균의 평균과 분산, 표본 분산의 평균과 분산

- 변수 변환법 : 확률 변수 함수에 대한 확률 밀도 함수를 구하는 방법

- 카이제곱분포 : 포본 분포에 대한 분포

이산형 변수 변환

- 통계량은 확률 변수의 함수

- 통계량 분포를 구하기 위해선 확률 변수 함수에 대한 분포를 구해야함

이산형 변수변환 예시 - 새로운 확률 변수의 확률 분포 구하기

연속형 확률 변수

- 이산과 달리 점확률이 존재하지 않으므로 누적 확률 분포를 사용하여야 함.

- 새 변수 Y에 대한 확률 밀도를 구해야하므로 미분하면 

연속 확률 변수 변환 예제

합과 평균의 확률분포

- 표본으로 구한 통계량들을 보면 확률 변수의 합 형태가 됨

=> 확률 변수 합의 확률 분포는 변수 변환법을 사용할수도 있지만 적률 생성 함수를 사용할수도 있음.

적률 생성 함수 성질

적률 생성함수 예제 1

- X_i ~ B(n_i, p)의 경우 X1 + X2의 확률 분포를 구해보자

적률 생성함수 예제 2

- Xi ~ Gamma(gamma_i, lambda), X1 + X2 + X3 + X4의 분포를 구해보자

카이제곱 분포

- 통계적 추론을 위해선 표본 평균과 표본 분산의 확률분포를 알기 위해서 필요한 분포로 카이 제곱, t분포가 있음

- 모분산 추정, 적합도 검정, 교차표 검정에 이용

- 감마 분포의 특수한 경우로 Gamma(r, lambda)에서 r = n/2, lambda = 1/2임

 => 확률 변수 X는 자유도 n인 카이제곱 분포를 따르게 됨.

*  원랜 비대칭적이나 자유도가 커질수록 대칭적으로 됨.

카이제곱 분포의 기댓값, 분산, 적률 생성함수

카이제곱 분포의 특성

- 정규 분포를 따르는 확률변수 Xi를 표준화 하고 제곱하면 자유도가 1인 카이제곱 분포를 따르게 된다.

- 확률 변수가 (n-1) 표본분산/분산인 경우, 자유도가 n-1인 카이제곱 분포를 따른다.

연속 확률 분포 continuous probability distribution

- 균등 분포, 정규 분포

- 지수 분포, 감마분포, 베타 분포, 카우치 분포 등

균등 분포 uniform distribution

- 확률변수 X = b - a

- a분에서 b분까지 기다리는 시간

균등분포의 확률밀도함수

균등 분포의 기댓값과 분산

지수분포 exponential distribution

- 사건이 첫 번쨰로 발생할때 소요되는 대기시간 T의 분포

       T ~ Exp(lambda)

지수분포와 포아송 분포

- 포아송 분포가 n이 충분히 클때 p이 0에 가까운 사건이 발생 횟수에 대한 확률 분포

- 버스 정류장에 한 시간에 5대씩 온다고 하면

- t 시간당 버스 도착 대수는 Poisson(5t)를 따른다고 할수 있다.

=> 쭉 전개해 나가면 지수 분포의 확률 밀도 함수를 구할 수 있다.

지수분포의 기대값, 분산, 적률생성함수

지수분포의 망각성

- a시간 동안 사건 발생 하지 않았다고 할떄, b를 더 기다리는 확률.

- 처음 a시간 만큼의 대기시간은 상관없음

지수분포 예제

- 노트북 수명 X가 평균 10년으로 Exp(1/10)을 따른다면, 5년 동안 사용한 노트북을 5년 더 사용할 확률

감마분포 gamma distribution

- r번쨰 사건이 발생할떄까지 대기시간 T의 분포

- T ~ Gamma(r, lambda)

* 감마분포도 지수분포와 마찬가지로 포아송 분포와 관련

감마 분포 예제

- 비행기 엔진이 두번째 결함이 일어나는 기간을 Gamma(2, 0.1)을 따를떄, 결함이 5년 뒤 나타날 확률

감마분포 기대값, 분산, 적률 생성함수

포아송/지수/감마, 카이 제곱 분포

- 포아송 분포 : n이 충분히 크고, p=0에가깝고, np=lambda일떄, 발생 횟수에 관한 분포 Poisson(lambda)

- 지수 분포 :  첫번째 사건이 발생할때까지 대기시간 T의 분포 Exp(lambda) = Gamma(1, lambda)

- 감마 분포 : r번째 사건이 발생할때까지 대기 시간 T의 분포 Gamma(r, lambda)

- 카이제곱분포 : Gamma(r, 1/2)

정규 분포 normal distribution

- 종모양의 대표적인 확률분포

- X ~ N(mu, sigma^2)

- 평균(기대값) mu : 위치 모수 location parameter

- 분산 : 척도 모수 scale parameter

정규분포의 적률 생성 함수

R 실습

1. 이항 분포

확률 변수

- 표본 공간을 수로 바꾸는 함수

확률 분포

- 이산형 확률 변수 : 베르누이 분포, 이항분포, 포아송 분포, 기하/초기하분포

- 연속형 확률 변수 : 균등분포, 지수분포, 감마분포, 정규분포 등

베르누이 분포

- 베르누이 시행 : 시행 결과가 두가지 중 하나 뿐인 시행

- 비르누이 시행의 확률 변수 X에 대한 분포

 ex. 불량품 여부, 찬성 여부

베르누이 분포 예시

- 게임 승리률이 60%라 가정할때, 승리 시 확률변수가 1 아니면 0인 경우 확률질량함수

베르누이 분포의 기대값, 분산, 적률생성함수

이항 분포 Binomial distribution

- n번 베르누이 시행을 독립 적으로 반복했을때 성공 횟수를 확률 변수 X로 할때의 확률분포

 ex. 동전을 n번 독립적으로 던진경우 앞면 총수

이항 분포의 예시 1

- 게임 승리율이 60%, 게임 3회시 승리 횟수(X)에 대한 확률 질량 함수는

이항 분포의 예시 2

- 위 예시에서 3번다 승리할 확률

이항 분포의 기대값, 분산, 적률생성함수

포아송 분포 Poisson distributioni

- 특정 기간/영역에서 사건이 일어날때 사건의 수를 확률 변수로 하는 분포

1. 이항분포에서 n이 충분히 크고

2. 성공률이 p가 0에 가까우며

3. 평균이 np = lamdba인 분포

포아송 분포의 기대값, 분산, 적률 생성 함수

모집단

- 우리가 알고자 하는 대상으로 불확실

- 불확실성을 확률, 확률 분포를 이용하여 측정

확률

- 확률 실험으로 나오는 일정한 비율(빈도론)을 확률 이해하기 시작

 ex. 동전 던지기, 주사위 던지기 등

표본공간 sample space의 예시

- 자동차 수명 

- 동전 던지기 실험

-> 확률 실험으로 구할수 있는 모든 케이스

사건

- 표본 공간의 부분집합

조건부 확률

- 사건 B가 발생한다고 가정할떄 A가 발생할 확률

조건부 확률 예시

- 주사위 눈이 짝수(A)가 나왔을때 3이하 수(B)가 나올 확률

S = {1, 2, 3, 4, 5, 6}

A = {2, 4, 6}

B = {1, 2, 3}

A 교 B = {2}

-> P(B|A) = 1/3

역확률 inverse probability

- P(A|B)를 P(B|A)로 바꿔주는것

베이즈 정리

- 표본 공간 B1, .. Bk로 나누고, A 발생을 가정할떄 Bi에 대한 조건부 확률

- "원인 B -> 결과 A"에서 "결과 A -> 원인 B"

배반

- 교사건이 존재하지 않는것

- 사건 A와 사건 B가 동시에 일어날 일이 없는 경우

독립 

- 교사건과 각 사건의 곱이 같은것

- 사건 A와 사건 B에 서로 영향을 주지 않음

P(A 교 B) = P(A) P(B)

독립 예제

- 500원 동전, 100원 동전을 던질때 사건 A, B가 독립인지 보자

* A: 500원이 앞면, B: 100원이 앞면

S = {HH, HT, TH, TT}

A = {HH, HT} -> P(A) = 1/2

B = {HH,TH}  -> P(B) = 1/2

교사건 = HH -> P(교) = 1/4

=> P(A) P(B) = 1/4 = P(교)

사건 A와 B는 독립

확률 변수 random variable

- 사건을 숫자로 변환해주는 함수

- 표본 공간을 정의역, 실수를 공역으로 하는 함수

확률 질량 함수

- 이산 확률변수 X의 분포

- f(x) = P(X = x), x = 0, 1, 2, ...

확률 밀도 함수

- 연속 확률 변수 X의 분포

- f(x) = d/dx F(x)

기대값 E(X)

- 확률 분포의 무게 중심

분산

- 모집단이 중심(기대값)으로부터 흩어진 정도)

결합 확률 분포 joint probability distribution

- 여러 가지의 확률 변수가 동시에 관측

 => 여러 확률 변수에 대한 결합 확률 밀도/질량 함수로 파악

결합 확률 질량/밀도 함수

- f(x, y) = P(X = x, Y = y)

주변 확률 질량/밀도 함수 marginal probability mass/density function

주변확률밀도함수 예시

기대값 성질

- E(aX + bY) = aE(X) + bE(Y)

- E(X1 + X2 + .. Xn) = E(X1) + . . . + E(Xn)

한개의 확률 변수를 다룰때

무게중심 기대값과 모집합이 퍼진 정도인 분산에 관심을 가짐

하지만 두개 이상의 변수인 경우

두 변수 간의 관계에 관심을 가져야 함

공분산 Covariance

- 두 확률 변수가 선형적으로 같이 변하는 정도의 측도

Cov(X, Y) = E([X - E(X)] [Y - E(Y)] )

             = E(XY) - E(X) E(Y)

상관관계 Correlation

- X의 단위는 명, Y의 단위는 kg 인 경우 공분산 값은 명 kg이 됨 => 표준화가 필요

- 표준화된 두 변수간 선형관계 척도

공분산 구하기 예제

X, Y가 독립 인 경우

- Cov(X, Y) = 0, Corr(X, Y) = 0

적률 Moment 생성함수

- E(X^K)승과 관련있는것을 만들어줌

- E(X)와 관련 있는것 -> 기대값

- E(X^2)와 관련 있는것 ->분산

- E(X^3) -> 왜도

- E(X^4) -> 첨도

=> 적률 :  기대값, 분산, 왜도, 첨도과 같은 것들

적률 생성 함수

- 모집단의 적률을 생성하는 함수

적률

- 확률 변수 X의 k승에 대한 기대값.

- 적률 생성함수를 k승 미분하고 t를 0으로 하면 구할 수 있다.

적률 예제 1

적률 예제 2 - X의 적률 생성 함수와, 1차 적률인 기대값

조건부 확률 밀도함수의 정의

통계학

- 주어진 데이터를 추론, 검정(통계폐키지 -> R, SAS 등)해서 의사 결정에 사용하는것

통계학의 원리를 수학과 시뮬레이션으로 일반화

- 통계적 추론에 대한 기본적인 이론과 구조 이해

- 확률 분포 이론에 대해서

- 추론 이론 : 빈도론자, 베이즈주의자(베이지안)

통계적 추론을 알려면?

- 수학을 이용한 연역적 방법

- 컴퓨터 시뮬레이션

- 통계학의 역사와 철학 :  어떤 원리로 발견되고 사용되었는지..

어떻게 통계적인 사고체계를 만들어갈것인가?를 중심으로 ...

통계적 추론을 하는 이유

- 세상은 불확실하다고 생각. 세상 일부를 관측해서 세상을 추론

- 통계적 추론의 예시 : 100만개의 꽃 씨가 있다. 어느 색 꽃의 씨인지 알수없으나 보라색 꽃의 씨 비율은?

- 불확실한 세상 : 확률로 나타냄

- 세상 일부 측정(표본, 실험, 관측 등) : 불확실한 세상 추론

이안 해킹

"통계학자는 생각하는 방법, 자기 견해를 내세우는 방법을 변화시켜서 세상을 바꾸었다."

통계학의 정의

- 데이터 측면 적 정의

 -> kendal, stuart : 자연 현상 성질을 측정한 데이터를 다루는 학문

- 불확실성 측면 정의

 -> Cox : 변동성, 불확실성 하에서 의사결정과 관련된 학문

 -> savage : 불확실성에 대한 학문

=> 불확실성, 불안전성, 변동성을 포함한 데이터로부터 지식을 일반화하고 효율적으로 사용할 수 있는 학문

- 통개학 개론에서의 정의 : 관심 대상에 대한 데이터를 요약 정리하여,

                                  불확실한 사실에 대한 결론이나 규칙성을 유도하는 방법

용어

- 통계학 출발점 : 관심 대상 전체가 아닌 일부만을 조사하여 전체를 파악

- 모집단 population : 알고자 하는 전체 집단(관심 대상)

- 표본 sample : 모집단 일부

- 모집단의 불확실성 -> 확률과 확률 분포로 나타냄

- 확률 : 0 ~ 1 값으로 사건 발생 가능성

  -> 빈도론적 확률 : 그 사건 횟수/ 전체 사건 횟수 => 빈도론자

  -> 인식론적 확률 (주관주의 확률) : 개인적 믿음 확률  => 베이지주의자

- 확률 변수 : 사건을 숫자로 바꿔주는 함수.

      ex. 동전 3개를 던질때, 앞면의 수(확률 변수 : 0, 1, 2, 3)

          주사위를 던질떄 나오는 수( 확률 변수 : 1, 2, 3, 4, 5, 6)

- 확률 변수 probability variable의 불확실성은 확률 분포로 표현

- 확률 분포 probability distribution : 몇개의 모수 parameter를 갖는 수학적 함수로 나타냄

   ex. N(mu, sigma^2), U(b, a)

통계량과 표본분포

- 통계량 statistic : 표본의 함수(표본 평균, 표본 분산)

- 표본 분포 sampling distribution : 통계량의 분포( 표본 평균의 평균과 분산, 표본 분산의 평균[=모 분산]과 분산)

추론 inference

- 알고있는 증거로부터 일정한 결론을 도출하는 방법

- 귀납적 추론 : 다수의 관측 증거로 결론을 도출하는것

- 연역적 추론 : 이미 밝혀진 명제로부터 결과를 도출하는것

통계적 추론 statistic inference

- 모집단으로부터 추출한 표본에서 모집단의 확률 분포(모수) 추측

- 이론적 부분 : 연역적 추론 

- 데이터 분석 : 귀납적 추론 ex. 여론 조사

통계 이론

- 내부를 알고있는 상자에서 공을 임의로 꺼냈을때 주황색 공 x개 나올 확률

 => 주사위를 던졋을때 1이 나올 확률

데이터 분석

- 내부를 모르는 상자에 공을 n개 꺼냇을때 x개가 주황색이라면, 상자에서 주황색공 비율

 => 여론조사 : 일부 사람들의 여론을 조사하여 전체 여론을 파악함

추론 inference 의 구분

- 추정 estimation

- 검정 test

통계적 추론 분야

- 확률 이론 : 확률 분포, 표본 분포

- 추론 이론 : 추정법, 검정법

빈도론자의 추론

- 2명의 인턴 중 1명 채용 예정. 

- 6개월 동안 20개 과제를 주고 성과의 평균을 비교

베이즈주의자 추론

- 과제를 순차적으로 주고, 과제별로 중요성을 다르게 봄.

- 중요성 높은 과제들을 많이 한 사람을 채용

Lindley의 통계적 추론 정의

- 통계학은 불확실성을 다루는 학문

- 불확실성은 확률로 측정

- 데이터 불확실성은 모수 조건에 따라 측정됨

- 모수 불확실성을 확률로 측정 -> 베이즈 추론, 이게 안하면 빈도론적 추론

- 추론은 확률 분포에 의해 수행

통계적 추론

- 모집단의 확률 변수 X ~ f(x|theta) (ex. N(mu, sigma^2)

- 표본 추출 : X1, X2, .. Xn ~ f(x|theta)

 * 서로 독립이고 동일한 분포를 갖는 확률 표본

- 모수에 적합한 통계량(추정량) 이용 : 대표적으로 표본 평균 bar{X}

- 통계량의 분포(표본분포)로 추정과 검정 수행 : 추정량 bar{X}의 분포 -> 정규분포, t분포

가능도의 원리 likelihood principle

- 표본의 가능도 함수에 표본으로부터 나타 수 있는 모수의 모든 정보를 가지고 있는 원리

 -> 모수의 정보를 가지고 있다고 생각.

     L(theta | x) = PI f(x_i | theta)

충분의 원리 sufficiency principle

- 표본을 요약한 통계략이 모수의 정보를 읽지 않는다는 원리

베이즈주의자와 빈도론자

- 빈도론자 : 모수는 고정

- 베이지안 : 모수는 확률적으로 분포

통계량 선택

- 평균제곱오차 MSE : 모수와 추정량 사이 손실함수의 기댓값

- 모집단이 정규분포일때, 표본 평균은 모평균을 추정하는데 있어 불편성과 효율성을 갖춘 좋은 통계량

통계 검정

- 귀무 가설 H0(기존의 사실)과 대립 가설H1(밝히고자하는 가설)

- 제 1종 오류(귀무 가설이 참인데, 이를 기각)와 제 2종 오류(대립 가설이 맞는데 이를 기각하지 못하는)

=> 최적검정 : 제 1종의 오류 기준 하에서 제 2종의 오류를 최소화 하는 검정

확률 과정 -> 마르코브 연쇄 -> 전이 연쇄

- 확률 과정 : 시간의 흐름에 따른 확률 변수 모임

- 마르코브 가정 : 미래에서의 확률 분포는 현재에 의존하지 과거에는 의존하지 않음

- 전이 확률 transition probability : 현재 상태에서 타 상태로 변화하는 확률

확률 과정 stochastic process

- X(t) : {X_0, X_1 ...}

- 시간 변화에 따르는 확률 변수의 모임

확률 과정의 예시

- 이산형 : 이용 손님 수

- 연속형 : GDP, 기온

확률 과정을 사용하는 이유

- X_{n+1}일때의 상태를 알고싶다!

마르코브 연쇄

- 간단한 확률 가정의 예시

- 미래의 상태는 현재 상태에 의존,

방통대 확률 과목을 듣고 있는데

내용은 몬테카를로 시뮬레이션 까지이긴 한데

이 확률 과목 내용들이 빅데이터 분석기사 시험 범위에서 기술 통계에 속하더라

그런데 여기는 표본 분포까지 다루지 확률 과정이나 몬테카를로 시뮬레이션까지는 다루질 않는다.

예전에 SLAM 공부 한답시고 원서를 시도때도없이 반복해서 보긴햇는데 여전히 잘 생각나지 않는다.

아무튼 확률 수업은 여기까지 대충 하고 다음은

통계학 부분에 대해서 공부하면 될거같다.

통계학 교과목 내용들 대부분이

추론 통계 파트와 많이 매치되더라

표본 비율의 분포

표본 분산의 분포

중심 극한정리

??

- 표본비율 : 원소가 0, 1로 구성된 모집단에서 추출한 표본들의 평균

 ex. 지지율, 찬성율

- 표본분산 : 모집단에서 추출된 표본의 변동성을 나타내는 통계량

 -> 모분산 추정시 사용

- 중심극한정리 : 표본 수가 증가하면 표본 평균이 정규 분포에 가까워진다.

표본 비율 분포 예시 - 지지율

- 1,000명 마을에 대표자 100명 선출.

- 정책 지지도를 구하였더니 100명중 60명이 찬성

- 한사람 한사람은 확률 변수. 각 확률 변수는 베르누이 시행 B(1,p)을 따른다. 

=> 모집단 : 1000명, 표본 : 100명. 지지율(표본 비율) : 60%

표본 비율

- 모집단 원소값이 0, 1인 경우에서의 표본 평균

표본 비율의 분포 구하기

표본 비율 기대값/분산 구하기

표본 비율

- 이항 분포 B(n, p)을 따르는 확률 변수 Sn(Sigma X_i)를 표본수로 나눈것

- 표본수가 커지면서 S_n은 정규분포에 가까워짐

이항 분포

- n이 큰 경우

표본 비율의 분포

- n이 클떄 정규분포에 근접해짐

이항분포의 예시

- 주사위 180번 던질떄 6이 나올 획수가 40이상일 확률

표본 비율 확률의 예시

- 모집단 흡연 비율 0.4인 학생 100명의 흡연 여부조사시. 흡연 비율이 50%보다 클 확률

표본 분산

카이제곱 분포 chi square distribution

- 정규 분포 N(mu, sigma^2)인 모집단에서 n개의 확률 변수 X1, X2 ..., Xn

- 정규 모집단에서 표본을 뽑았다는 가정

잠깐 중간부터 좀 꼬이기 시작하는데

표본 분산이고, 표본 평균의 분산, 표본 분산의 분산 왜이렇게 얘기되는지 햇갈려서

존이 님의 블로그 참고

blog.naver.com/mykepzzang/220850395100

1. 모집단에서 확률 표본 x1, ... , xn을 추출

2. 표본평균과 표본 분산을 다음과 같이 구할 수 있음.

3. 표본 평균을 새로운 확률 변수로 보자 -> 표본 평균의 평균과 표본 평균의 분산을 구할 수 있음.

ex. 평균 신장

 -> 서울 평균 신장, 대구 평균 신장 등 다 다르므로, 지역별 평균 신장으로 평균과 분산을 또구해볼 수 있다.

* 표본 분산의 기댓값은 모집단의 분산과 같다고 한다!

중심극한정리 total central theorem

- 평균 mu와 분산 omega^2인 모집단에서 n개의 표본을 뽑았을때

- 표본이 커질수록 표본 평균은 정규 분포를 따르게 된다.