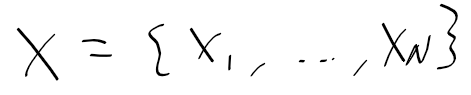집밖은 위험해

분할 통치법 divide and conquer

- 성능 좋은 알고리즘을 설계하기 위해 널리 사용됨

- 해결하려는 문제(크기 n으로 가정)를 작은 여러 문제로 분할

 => 원래 문제의 답을 쉽게 얻는 방향으로 분할 필요

- 분할된 문제를 해결후 간단한 처리로 통합함

분할 통치법의 예시

1. 합병 정렬 merge sort

2. 하노이의 탑

좋은 알고리즘

- 좋은 알고리즘들은 문제해결 방법과 고속화 기법에서 공통점이 많음

좋은 알고리즘 - 퀵 정렬과 합병 정렬의 예시

1. 데이터가 있는 배열을 두개로 나눔

2. 두 배열을 각각 정렬

3. 그 두 배열을 연결

=> 이를 알고리즘 설계 기법 이라고 부름

개발자와 알고리즘 설계

- 해결해야할 새 문제가 발생할때 기존 알고리즘 설계 방법을 응용할수있는지 고민하는것이 새로 개발하는것보다 줄일수 있어 중요

알고리즘 설계 기법의 종류

1. 분할 통치법 divide and conquer

2. 균형법

3. 동적 계획법 dynamic programming

4. 탐욕법 greedy algorithm

5. 백트래킹법 dacktracking

6. 근사해법 approximation algorithm

표본 공간 sample space

- 통계 실험 trial에서 발생가능한 결과들의 집합. S로 표기

- 표본의 값이 이산적이라면(ex. 주사위 숫자) 이산 표본공간

- 표본의 값이 연속적이라면(ex. 시간) 연속 표본 공간

사건 event

- 표본 공간의 한 원소나 원소들의 모임(부분집합)

확률의 고전적 정의

- 고전적 의미의 확률 P(A) = 사건 A의 모든 원소 수(k) / 표본 공간 S 전체 원소 수(n) = k / n

* 개념적 정의 : 어느 사건이 일어날 가능성에 대한 척도

고전적 확률의 문제

- 모든 원소들의 발생 가능성을 동일한 것으로 봄.  ( ex. 동전 앞뒷면의 확률, 주사위 숫자의 확률)

   => 하지만 이런 경우는 매우 드물며 고전적인 확률을 사용할 수 없음.

공리적 학률

- 수학자 콜모고로가 다음의 세 공리를 만족시키는 경우. 확률 P(A)에 대해 공리적 확률 정의

1. 0 <= p(A) <= 1

2. P(S) = 1

3. A1, ..., Ai 등 이 서로 배반이면(교집합이 공집합이면)

=> P(A)는 표본 공간 S에서의 사건 A에 대한 공리적 확률

- 사건 P가 0 ~ 1사이의 값이며, 전체 P의 합은 1이 되고, 각 사건의 합집합이 P의 합과 같으면(교집합이 없다) 

 => 확률 P(A)는 공리적 확률

 * 상대도수의 극한화 : 상대도수에서 횟수 n을 무한대로 늘림.

확률 probability

- 불확실한 가능성을 측정한 정도

확률과 도박문제

1. 상황 : 승률이 0.5인 도박, 도박사 A, B가 각 32피스톨(화폐)를 걸고 시작

2. A가 2번이기고, B가 1번 이김 -> 중지

 => 어떻게 해야 공평할까?

3.  2번이긴 A에게 64 * 2/3 = 42.7 , 1번이긴 B  64 * 1/3 = 21.3에게 주는것은 불공평(페르마)

4. B가 돈을 다 받으려면 2번 이겨야함 -> 확률 : 1/4

5. A가 돈을 다받으려면 1번만 이기면 됨 -> 확률 : 1 - (1/4) <- B가 우승할 확률

6. 결론 : A = 64 * 3/4, B = 64 * 1/4

   => 기댓값

동전 확률의 상대 도수 relative frequency 적 정의

- 동전의 앞면이 나올 확률 1/2

- 동전이 여러번 던질때 앞면이 나올 확률을 아래와같이 상대도수적으로 정리 가능

확률의 상대 도수적 정의

- n번 시행(도수)했을떄 사건 A가 발생한 확률 P(A)는 A가 a만큼 발생한 경우 아래와 같이 정의

기하학적 확률

- 그동안 안 확률들은 모든 사건들이 일어날 확률이 같다고 가정하고 다룸

 => 발생 가능한 사건이 3개가 있다면, 각 사건들의 발생 가능성은 1/3이라고 보는것

- 하지만 표본 공간에서 많이 차지하는 사건이 있고, 적게 차지하는 경우도 많음

- 기하학적 확률 : 전체 공간의 면적을 S, 사건 A의 면적을 a라 할때 기하학적 확률은 아래와 같이 정의

주관주의 확률 예시 degree of belief

- 두 줄이 있을때 내가 선 줄과 다른 줄 둘중 하나가 먼저 줄어들 확률은 0.5, 0.5로 반반

- 줄이 10개가 있다면 내 줄이 가장 먼저 끝날 확률은 1/10. -> 내가 늦어질 확률은 9/10

=> 주관적 확률과 과학적 확률 사이에 차이가 존재. 비합리적인 행동을 하게됨.

확률의 종류

- 크게 주관적 확률과 객관적 확률(상대도수적 확률, 기하학적 확률)로 구분 가능

1. 상대도수 relative frequency, 빈도주의적 확률 : 전체 사건 발생 횟수 중에 몇번 발생했는가?

2. 기하학적 확률 geometric : 해당 사건이 전체 공간에서 얼마나 차지하는가?

3. 주관주의 확률 degree of belief : 객관적으로 구할수 없으나 주관적으로 생각하는 확률

수학

- 현실의 문제를 추상화하여 해결하기 위한 과학적 언어

수학의 종류

- 대수학 algebra : 수학의 일반적인 성질을 연구하는 분야

- 해석학 analysis : 미분과 적분을 이용하여 함수의 연속성을 탐구하는 학문

- 기하학 geometry : 공간에 존재하는 도형의 성질(ex. 치수, 모양, 상대적 위치) 등을 다루는 학문

                       => 다루는 대상으로 점, 선, 면, 도형, 공간 등 존재

- 위상수학 topology : 연결성이나, 연속성, 작은 변화에 의존하지 않는 기하학적 성질을 다룸

- 이산수학 discrete mathematics : 정수, 그래프, 논리 연산 처럼 연속되지 않은 서로 구분되는 값을 다루는 학문

- 확률론 probability theory : 확률에 대해 연구하는 분야. 통계학의 기초

                           => 비결정론적인 현상 nondeterminsitic phenomenon을 수학적으로 표현하기 위함.

- 통계론 statistics : 산술적인 방법을 이용하여 다량의 데이터들을 관찰하고, 정리 분석하는 분야

컴퓨터 과학의 분야들

- 계산 이론 theory of computation : 어떤 문제들을 푸는게 가능한지. 어떻게 효율적으로 푸는지 다루는 학문.

                          => 계산 가능성 이론과 계산 복잡도 이론으로 나뉨 + 추상 기계(튜링 머신)을 다룸

- 시스템 아키텍처 system architecture : 시스템 구조, 행위 등을 정의하는 개념적인 모델링하는 학문

- 컴퓨터 그래픽스 Computer Graphics : 컴퓨터를 이용해 실제 영상을 조작하거나 새로운 영상을 만드는 기술

- 계산 과학 : computational science : 과학/공학 문제를 수치적 방법과 컴퓨터로 푸는 분야

     => 계산 과학에서 주로 사용하는 방법들 : 수치 해석, 룽게 쿠타방법, 몬테카를로 방법, 퓨리에 변환, 뉴턴 방법 등

집합 set

- 서로 구별할수 있고 명확히 정의된 것들의 모임

원소 element

- 집합을 구성하는 요소들

원소의 표기법

- 원소 나열법 : 집합과 원소들 전체를 나열한 것

- 조건 제시법 : 집합에 속하는 원소들에 대한 조건을 써서 보여주는 방법

- 아래의 그림은 원소 나열법의 예시(패턴인식). 특징 벡터 X의 원소로 x1, x2, ...., xn이 존재하는데 원소나열법으로 표기

부분집합

- 일부 원소들의 모임

- 위 그림의 예시를 들자면 x1 ~ x3까지의 원소들이 Y라는 집합을 구성한다고 하자 Y는 집합 X(특징 벡터)의 부분집합임

* 내가 넣고 싶은 내용만 넣다보니 생략한것도 많습니다.

확률

- 특정한 사건이 발생할 가능성을 나타내는 척도

고전적 의미의 확률

- 표본 공간 sample에서 사건 event에 속하는 원소들이 차지하는 비율

=> P(A) = 사건 A의 원소 갯수 / 표본 공간에 존재하는 전체 워소의 갯수

함수

- 두 집합에 속하는 원소간의 관계

- ex. y = f(x)

함수 관련 표기

- 집합 X에서 Y로의 함수 f => f : X -> Y

    * 즉 함수 f는 집합 X에서 Y로 대응 관계를 가짐 => x값을 주면 y값으로 바꿔준다 ! ==  y = f(x)

    * 위 개념은 선형 대수나 공업 수학 등에서 많이 나오는 형태이므로 꼭기억하자

    * 생긴건 되게 간단하고 뭔뜻인지 알거같은데 정확하게는 몰라서 힘들었다 ...

정의역 치역 공역

- 위에서 집합 X에서 Y로의 함수 f에 대한 표기 f : X -> Y를 살펴보았는데

- 여기서 집합 X를 정의역, Y를 공역이라 한다.

 * 정의역은 함수 f의 입력이 되는 집합, 치역은 x를 입력했을때 함수 f의 출력이 되는 집합!!

- 정의역 X의 원소가 함수 f를 통해 대응되는 집합 Y 원소들의 모임(부분집합)을 치역이라 부름

전사, 단사, 전단사, 역함수

기함수 우함수

- 우함수 even function : f(-x) = f(x) => 좌우 대칭인 함수

- 기함수 odd function : f(-x) = -f(x) => 좌우 상하 대칭인 함수

초월함수 transcendental function

- 시간에 따라 선형적으로 증가가 아니라 갑자기 증가하는 형태를 가짐

- 아래의 그림은 초월 함수의 예시들

대수함수 algebraic function

- +, -, *, /과 같은 대수연산으로 이루어진 함수

수학 mathmetics

- 수학은 현실의 문제를 추상화하여 해결할수 있도록 문제를 정의할수 있는 과학의 언어

수학의 연구

- 고대 그리스 시대부터 본격적으로 연구

 -> 플라톤이 기하학을 모르면 공부하러 오자말라고 할정도

- 유클리드의 "element"가 과거 수학의 교과서 역활 함

- 17세기서 페르마, 데카르트, 파스칼, 뉴턴 등의 수학자들이 나옴

뉴턴과 라이프니츠의 업적

- 미적분학 등 해석학의 발전에 기여

 -> 수학은 추상화 일반화 경향이 커짐.

수학의 분류

- 순수 수학 : 추상화된 문제를 해결하기 위한 이론 세움

- 응용 수학 : 물리학, 공학, 사회과학 에서 필요

        -> 순수 수학으로 얻은 이론을 현실 문제에 적용. 문제를 추상화하여 현실에 적용

쾨니히스베르크의 다리문제

- 두 섬과 육지 사이 7개 다리를 한번에 건널수 있는 길 찾기

 => 찾지 못함. NP완비와 관련

- 오일러는 이걸 한붓 그리기 문제로 단순화하여 산책로가 없음을 증명

쾨니히스베르크의 다리문제로 얻을수 있는 통찰과 수학을 이용한 문제 해결

1. 오일러는 다리 문제 추상화

2. 한붙 그리기 문제로 변환

3. 한붓 그리기가 가능한지 수학적 정리로 적용

4. 불가능함을 증명

수학을 이용한 현실 세계와 추상적 세계의 관계

- 현실 세계 -> 추상화, 문제화 -> 추상적세계

- 현실 세계 <- 해결, 적용 <- 추상적 세계

정의 theorem이란?

- 추상화된 문제는 수학자들이 발견한 중요한 결과. 수학적 정리로 해결.

- 정리 : 사전에 옳다고 정의

   => 정리는 특정 사실(가정)을 옳다고 생각하면 결론이 참이 된다라는 명제의 형태를 띔

- 명제 :  P이면 Q이다.

- 대우명제 : Q가 아니면 P가 아니다와 같이 명제의 반대화된 경우를 말함

수학적 명제의 증명 방법들

1.  연역법

     - 일반적으로 알려진 이론을 어떠한 현상에 대입시켜 이에 대한 결론을 도출해내는 방법

2. 귀류법

     -  명제의 참을 증명하기 힘들때, 명제가 거짓이라 가정하고 그 명제가 모순됨을 보임

          => 원 명제가 참이라 할수 있음. 간접 증명법

3. 수학적 귀납법 mathmetical induction

    - 특정 명제가 참임을 증명하고, 다음 명제가 참임을 보여주고, 모든 겨우에 참임을 증명하는 식

    => 이미 알려진 것을 논리적으로 다시 증명하는 방법

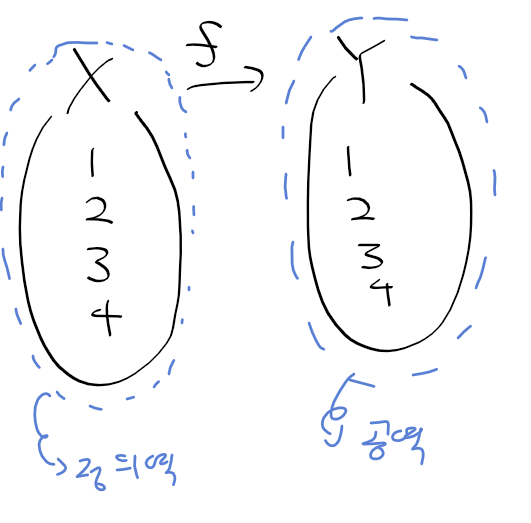
집합 set

- 특정 규칙을 따르는 원소들의 모임

체 or 장(field. -> ex. vector field, likelihood field)

- 실수의 기본 성질들을 만족하는 집합

구간 interval

- 구간의 양 끝점을 포함하느냐에 따라 달림

- 열린 구간 open interval : 끝점을 포함하지 않는 구간

      => 표현 : a < x < b      (a, b)

- 닫힌 구간 closed interval : 끝 점을 포함하는 구간

      => 표현 : a <= x <= b      [a, b]   

상항, 하한(상계, 한계)

- 상한, 상계 upper bound : x <= a에서의 a

- 하한, 한계 lower bound : a <= x에서의 a

좌표계와 방정식

- 좌표계 : 수가 주어질때 수들의 순서쌍을 좌표상에 나타내는 공간

- 방정식 : x, y 수들의 대응 관계를 표현한 수식

1. 데카르트 좌표계(직교 좌표계, 카티지안 좌표계)

 - 일반적으로 사용하는 x, y좌표계

 - 직교 좌표계, 카티지안 좌표계라고도 하며 수학자 데카르트가 제안한 좌표계

2. 방정식(그래프) equation

 - 직선의 그래프(선형)

 - 곡선의 그래프, 원그래프(비선형) 등 다양한 그래프들이 존재

최근 컴퓨터 비전과 패턴 인식 학습을 하면서

확률적 로봇공학과 마찬가지로

공업수학을 배운 이후가 배우기 전에 봤을때와

이해할수 있는 정도가 확실히 달랐다.

하지만 여전히 수식 각각의 의미는 알겠지만

수식들이 연결되어 알고리즘을 이루어지는 형태가 잘 눈에 익지는 않는다.

그래서 공학 분야에서 수학 전반을 정리해볼 필요가 있을것 같아

대학수학을 정리하고자 한다.

이제 슬슬 실습도 필요하긴 한데,

실습을 시작하기전에 잠시

이론적인 내용들을 다루는 시간을 더 갖고자 한다.

대학 수학, 통계, 확률론 정도 빠르게 정리하고 나서

실습 내용들을 넘어가면

지금 바로 실습 정리하는것 보다 훨씬 완성도 있게 글을 쓸수 있을것 같다.

우선 지금 할 내용들은 대학 수학의 전반에 대해서

당장 재정리할 부분만 빠르게 보고 넘어가려고 한다.

대학 수학의 구성

1 수학의 기초

2. 집합과 함수

3. 수열과 극한

4. 미분

5. 적분

6. 행렬과 벡터

7. 연산

등으로 정리할수 있을것같다.

수학이 왜필요한가

현대 자연/사회 과학 등의 분야들은 다 수학의 개념들을 기반으로 발전했고

수학이란 언어를 통해서 연구를 제시하고 문제를 해결할 능력을 키울수 있게 되었다.

전문적인 수학의 한 분야 처럼 깊이 있지는 않더라도

우리가 배워야할 부분, 알아야할 부분이 어디까지 있겠는지 생각을 정리할수 있으면

이번 대학 수학 정리를 마무리 할수있을것같다.

추정, 추론 estimation, inference

- 표본 집합 데이터들로 정확하지는 않으나 값을 구하나는 행위

패턴인식에서의 추정

- 수집된 표본으로부터 확률 밀도 함수를 추정은 패턴을 인식하기 이해서 매우 중요

- 유한개의 표본들로 클래스별 확률 밀도 함수 추정해야함

베이즈 정리

- 사후확률 계산하려면 우항의 우도, 사전확률을 알아야함.

- 사전확률 : 이미 알고있는것으로 정의될수 있음

- 우도 : 해당 클래스의 확률 밀도 함수로 표본 데이터를 이용하여 추정 필요

데이터 밀도 추정 방법

- 모수적 방법 parametric method

     주어진 데이터 집합(샘플 데이터들)이 이루는 확률 밀도 함수가 가우시안 같은

    특정 형태로 이루어진것을 가정하고, 확률밀도 함수의 평균, 공분산 등의 파라미터 추정한는 방법. 

      => 샘플 데이터가 특정 분포를 따른다 가정하여, 그 분포의 파라미터 추정 (ex. 최우추정법 MLE)

- 비모수적 방법 non parametric method

   주어진 데이터가 아무 분포를 따르지 않고, 데이터로 직접 밀도 함수를 구하는 방법.

    * ex. 히스토그램, KNN, KDE 커널 밀도 추정

최우추정법 최대 우도 추정, MLE Maximum Likelihood Estimation

- 아래와 같이 M개의 파라미터 집합과 확률 밀도 함수 P(x | Theta)로 관측된 표본 데이터 집합 x가 주어질때 파라미터들을 추정하는 방법

  => 샘플 데이터로 특정 확률 분포의 파라미터 추정

- 어느 프로세스로 발생된 데이터로 이루어진다면, 전체 표본집합은 결합확률 밀도로 다음과같음.

- 위 식에서 P(x|Theta)는 파라미터 Theta를 따르는 주어진 데이터 집합의 우도 함수.

- 위 함수는 확률 함수. 가장 큰 확률 갑을 구하는 Theta를 hat{theta}로, 우도 함수의 곱을 합으로 바꾸게 log를 하자

 => 이 식은 로그 우도 함수 log likelihood function.

 => 로그 우도 함수를 최대로 하는 파라미터 hat{theta}가 미지의 파라미터를 가장 잘 추정해냄

로그 우도 최대화 maximization of log likelihood

- 로그 우도를 최대화 하기 위해서 Theta에 대해서 편미분 하자.

- 아래의 그림은 1차원 데이터에 대해 많은 후보 확률 분포가 나타냄.

- 다음 그림은 결합 밀도 함수로 구한 우도 함수 p(D|Theta) (D는 dataset)

  * 우도를 최대화 하는 파라미터에 hat{theta} 표기가 됨

- 다음 그림은 로그 우도 함수. 최우도 hat{theta}의 위치가 우도인 경우와 동일함

MLE 최대 로그 우도 추정법으로 최대 로그 우도 구하기

- 파라미터 벡터를 다음과 같이 가정

- 로그 우도의 그라디언트를 구하면

 * hat{theta}가 로그 우도를 최대화 하는 파라미터

최우 추정하기

1. 표본 집단의 로그 우도 구하기

2. l(theta)를 모든 파라미터로 편미분 한 후, 우항을 0으로 하여 최우 방정식으로 만듬

3. 연립 방정식을 풀어 해를 구한다.

4. 해 중에서 최대값을 추정 파라미터 hat{theta}로 쓴다.

가우시안을 따르는 샘플 데이터로부터 파라미터를 최우추정법으로 추정하기

- 표본 데이터가 단변량이라 가정

- 우리는 이 샘플 데이터가 가우시안 분포를 따른다 가정하고 가우시안 분포의 파라미터를 추정할 것임

 => 단변수 가우시안 확률 밀도 함수의 로그 우도는 아래와 같음.

- l(theta)의 그라디언트는 다음과 같음

- 그라디언트 우항을 0으로 하여, 최우 방정식을 만들자. 로그 우도를 최대로하는 첫번쨰 파라미터는 표본평균

- 로그 우도를 최대로하는 두번쨰 파라미터는 표본 분산

- 결론 : 주어진 샘플 데이터의 평균과 표본 분산이 로그 우도를 최대로 하는 파라미터

판별함수 discriminant function g(x)

- 앞서 살펴본 모든 결정규칙, 결정 함수, 결정 경계들은 동일한 구조

- 모두 g(x)를 최소화 하거나 최대화하는 클래스 omega_i를 선택

- 즉, 아래와 같이 정리할 수 있음.

- C개의 클래스 중 하나를 결정하는 시스템이 주어지면, C개의 판별함수 중 가장 큰 값을 가지는 클래스 선택

각 기준별 판별함수 일반항

- 베이즈, MAL, ML 기준의 판별함수 일반항은 다음과 같다.