선형대수(복) - 1. 벡터론

벡터 vector

- 크기와 방향을 가지는 물리량

특징 벡터 feature vector

- 차원을 가지는 벡터

벡터의 전치 transeposed vector

- 벡터의 원소를 행과 열을 바꾼것

 

벡터의 크기, 노름 norm

- 원점에서 벡터공간상 한점까지의 거리

 

 

단위 벡터 unit vector

- 특정 방향에 대해 길이가 1인 벡터

 

 

 

벡터의 연산

1. 스칼라 곱

- 벡터에 스칼라(실수) 곱하는 연산

2. 내적 dot product

- 점으로 표기하기 때문에 점곰, 혹은 결과가 스칼라이므로 스칼라 곱, 꺽쇄를 사여 표기하기도 함.

3. 외적 cross product

- 벡터끼리 곱하여 벡터가 나와 벡터 곱, 교곱이라고도 부르는 연산

- 자세한 연산은 공업수학 참조

 

 

 

 

수직 사영 projection

- 벡터 y를 벡터 x에 사영하면, x방향의 벡터가 생김

 

 

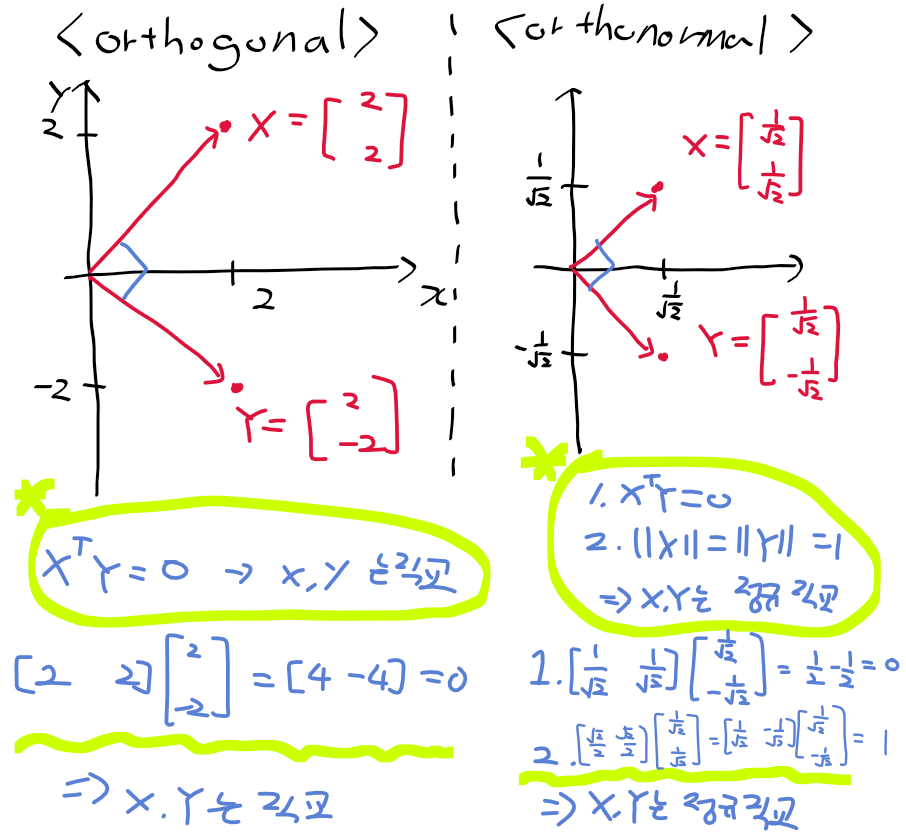
벡터의 직교(수직)과 정규 직교

- 아래의 조건을 만족하는 경우 두 벡터 x, y는 수직 orthogonal/정규 직교 orthonormal이됨.

 

 

 

선형 결합 linear combination

- 벡터 집합과 스칼라 계수 집합들의 곱, 합이 선형성을 가지고 있으면 선형 결합. 1차결합이라고 부름

 

 

 

선형 독립과 선형 종속

- 아래의 벡터 집합과 스칼라 계수 집합이 주어질때

- 선형 독립 : 모든 a_i = 0인 경우에만 성립하는 경우. 벡터 집합은 선형 독립 linear indepent

- 선형 종속 : 선형 독립이 아닌 경우. 선형 종속 linear dependent

 

 

 

기저 

- 스칼라 곱을 해서 벡터 공간을 생성할수 있는 벡터

- ex

  기저 벡터 : (1, 0)가 주어질때

   a (1, 0) => (2, 0), (3, 0), (4, 0) 등의 생성 벡터 공간(span vector space)이 만들어짐

https://losskatsu.github.io/linear-algebra/basis/#2-%EC%A2%8C%ED%91%9C%ED%8F%89%EB%A9%B4%EC%97%90%EC%84%9C%EC%9D%98-%EA%B8%B0%EC%A0%80

 

기저 집합

- 2차원에서의 기저 (1, 0), (0, 1)

- 3차원에서 기저 (1, 0, 0), (0, 1, 0), (0, 0, 1) 과 같이

 벡터 공간을 생성해내는 기저의 모임

 

 

그램 슈미트 직교화 과정

- n개의 선형 독립 벡터가 주어질때, 생성 벡터공간에 대한 정규 직교 기저를 찾을 수 있음

- 아래의 경우 3개의 선형 독립 벡터(u1, u2, u3)가 주어질때 생성 벡터(v1, v2, v3) 공간을 보여줌