모집단 population
- 관심의 대상 전체
표본 sample
- 모집단의 일부분
모수 parameeter
- 모집단은 특정 분포를 따름
- 모집단의 특성을 나타내는 값(모집단이 변경되지 않는 이상 상수)
통계값
- 표본으로부터 얻은 값
* ex. 임의로 선정한 1000가구의 평균 지출이 100만원인 => 100만원이 통계값
통계량 statistic
- 통계 값을 구하기 위한 수식
- 대표적인 통계량으로 표본 평균
표본 평균 구하기
- 확률 변수 X1, ..., Xn가 평균 mu, 분산 sigma^2인 모집단에서 추출된 경우
- 모집단의 평균 mu를 추정 inference 하기위한 표본 평균은 아래와 같음

주사위에 대한 확률 분포와 모수 구하기
- 주사위는 1 ~ 6까지 확률 변수값을 가지는 이산 균일 확률 분포를 따름
=> 모집단의 평균과 분산은 다음과 같이 구함

표본 크기가 2인 경우 주사위 표본 평균 구하기
- 이번에는 확률 변수 X1, X2가 주어질때 표본 평균을 구하면 다음과 같이 정의함
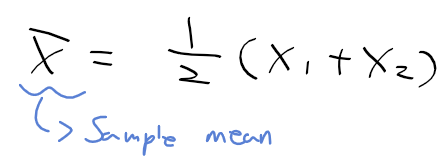
- X1과 X2가 아래와 같이 주어질때 표본 평균 bar{X}는 아래와 같다.

표본의 크기가 2인 표본 평균의 확률분포표
- 주사위를 두번 던질때 얻을수 있는(X1, X2의 조합) 표본 평균에 대한 확률 분포표는 아래와 같다.

표본의 크기가 2인 표본의 통계값
- 위 표본 평균에 대한 확률 분포가 주어질때 기대값과 분산은 아래와 같다.

=> 모 평균과 표본 평균은 7/2로 동일하나 표본 분산은 모 분산의 1/2가 됨.
표본 크기가 n인 표본 평균 bar{X}의 기댓값과 평균
- 다음과 같이 n개의 표본들이 주어질 때

- 이들을 샘플링하여 뽑은경우 표본 평균 bar{X}의 기댓값과 평균은 아래와 같다.

=> 1. 모 평균과 표본 평균은 동일
2. 표본 분산은 모 분산/n
대수의 법칙
- 표분의 수가 커지면 표본 평균 bar{X}는 모 평균 mu에 수렴
모집단이 정규분포일때 표본 평균 분포
- 표본 평균은 모집단을 추정하는데 사용되므로 매우 중요
- 모집단이 정규 분포를 따르면 -> 표본 평균도 정규 분포를 따름

중심 극한 정리 central limit theorem
- 모집단이 정규 분포가 아니어도 표본 n이 충분히 크면 표본 평균은 정규 분포에 근사

'수학 > 공업수학, 확률' 카테고리의 다른 글
| 확률 - 10. 몬테 카를로 방법 (0) | 2020.08.13 |
|---|---|
| 확률 - 9. 확률 과정 (0) | 2020.08.13 |
| 확률 - 7. 다변량 확률분포 (0) | 2020.08.12 |
| 확률 - 6. 연속 확률 분포 (0) | 2020.08.12 |
| 확률 - 5. 이산 확률 분포 (0) | 2020.08.12 |