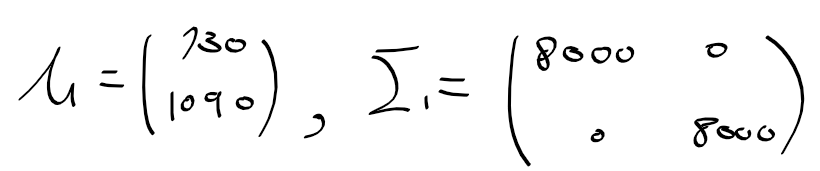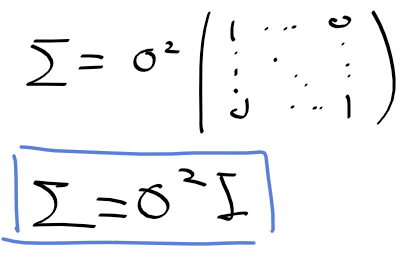집밖은 위험해

베이즈 기준  bayes criterion

- 베이즈 위험을 최소화하는 LRT 결정규칙

MAP 기준

- 비용 값이 1이나 0인 zero-one 비용 함수를 사용하면 베이즈 기준이 P(omega_i | x)의 비가 됨

 => 사후확률을 최대화 시키므로 사후확률 최대화 Maximum A Posterior(MAP) 기준

 * 우도비가 아니라 최대화된 사후확률이 결정 함수가 됨

ML 기준

- 사전 확률 P(omega_i)가 같고, zero-one 비용 함수인 경우

 => P(x | omega_i) 우도비로 바로 표현이 가능. 우도비를 최소화 하므로 ML Maximuum Likelihood 기준이라 함.

통계 결정이론에 대한 정리

- 먼저 우도비 검증을 통해 결정 규칙(결정 함수)를 구하는 과정에 대해서 정리.

- 오류 함수로 우도비 검증 방법이 아니라 오류 함수를 최소화 하는 방법으로 결정 규칙을 찾을수 있음을 확인.

- 그동안 사용한 확률은 잘못된 확률에 대해 동일한 가중치(비용)을 부과, 서로 다른 비용을 주고 이에 대한 기댓값이 베이즈 위험, 베이즈 위험을 최소화하도록 하면 결정 경계를 정할수 있었음.

- 이러한 베이즈 위험을 활용한 결정 규칙 방법에 대해 베이즈 기준, MAP 기준, ML 기준 등 확인함.

- 베이즈 기준은 베이즈 위험을 최소화하는 RLT 결정 규칙, MAP 기준은 제로-원 비용함수를 사용하여 사후확률 표현으로 구한 결정 규칙. ML 기준은 제로-원 비용함수를 따르고, 모든 사전확률이 같다고 가정하여 바로 우도로 나타냄.

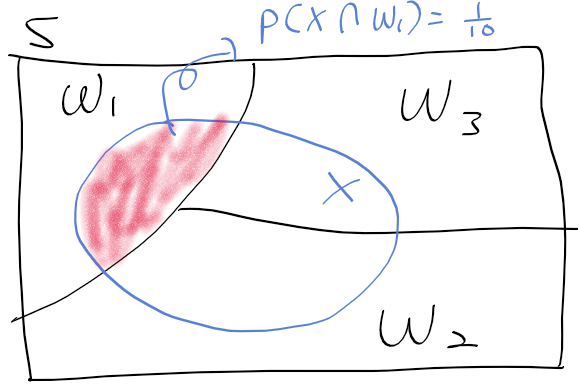
오류 확률이용한 다중 클래스 결정 규칙

- 이전에 본 결정 규칙(결정 경계, 결정 함수)에 대한 문제는 클래스가 2개인 경우만 다루었음. 하지만 다중 클래스 문제로 쉽게 일반화 가능

- 오류 확률과 옳은 확률 표현부터 시작하자

 => 오류 확률 최소화는 옭은 확률 최대화와 동일한 표현

- P(correct)를 사후확률로 표현하면

- 옳은 확률 최대화 하기 위해 적분결과인 gamma_i를 최대화 해야한다.

 - 각 적분 gamma_i들 중 p(omega_i | x)를 최대로 하는 omega_i를 선정하면 그 영역 R_i가 옳은 확률 최대영역

=> 오류 확률 최소화하는 결정규칙 = 사후확률 최대화 MAP 기준

베이즈 위험 bayes risk

 - ex. 1. 암환자를 잘못 오진해서 음성이라 판단한경우 위험이 크다

       2. 암환자가 아닌 사람을 오진해서 양성이라 판단한 경우 위험은 작다.

 => 잘못 분류하나 경우 벌점을 고려해야함.

- 벌점(비용) cost ( C_ij ) : omega_j 클래스를 omega_i로 골랐을때의 비용

- 벌점(비용)의 기대값 = 베이즈 위험

베이즈 위험 정리

- 비용의 기대값인 베이즈 위험은 아래와 같이 정리할 수 있다.

- 베이즈 위험을 최소화 하기 위해선 아래와 같이 잘못 판단한 경우에 대한 확률이 최소가 되어야 한다.

- 이를 전개해보면

- 모든 영역에 대해 우도를 합하면 1이므로 아래가 성립

- 위 성질과 전개한 결과를 정리해서 다음과 같이 표현하자.

- 이를 정리하면 아래의 식을 구할수 있으며, 앞의 두 항은 R1구하는데 필요없는 상수이므로 생략 가능

 => R을 최소로하는 R1을 구하면 되겠다.

베이즈 위험을 이용한 결정 영역 최소화 정리

- 위 결정영역 R에 대한 식을 R1을 최소화 시키는 값을 구하는 바꿔보자

분류기

- 특징 공간 feature space를 결정 영역으로 나누는 기술

베이즈 분류기에서의 에러

- 특징 공간을 R1, R2로 분류시 omega_1을 R2로, omega_2를 R1으로 잘못 분류하는 경우 존재

- 위 식을 2가지 경우가 아니라 여러가지의 경우에 대해서 간략화 시키면

- 각 클래스가 주어질때 오류에 대한 확률은 아래와 같이 정리

2클래스 분류에서의 오류 확률

- 위 정리를 이용해 오류 확률 p(err)을 아래와 같이 정리된다.

- 앱실론 1과 앱실론 2를 확률 밀도 함수에 대한 그래프로 나타내면

- p(error)의 사전확률 p(omega_1) = p(omega_2) = 0.5인경우, p(err)는

오류 확률로 결정경계 구하기

- 오류확률 P(err)을 사후확률 P(err | x)로 표현하자.

- 최적의 결정 경계를 구하기 위해, 오류 확률이 최소가 되어야 함

 => 최소의 p(err | x)를 구해야 한다.

점 x*이 주어질떄 오류확률

- 점 x*이 주어질떄 오류에 대한 확률 p(err | x*) = omega_2를 omega_1으로 잘못 분류할 확률

 => P(err | x*) = P(omega_1 | x*)

- x*이 결정 경계가 된다면 파란색의 영역이 커져 최적의 결졍 경계가 아님.

 => 결정경계는 X_B에서 적분 값이 최소가 됨.

베이즈 오류률 bayes error rate

- LRT 결정 규칙과 동일한 지점인 결정 경계 X_B에서 오류 확률 P(err)이 최소가 됨

 =>  베이즈 오류율 : 결정 경계에서 최소가 되는 오류 확률 p(err)

확률 밀도 함수 모델링

- 어느 데이터 분포가 존재할때, 평균과 공분산 파라미터로 이루어진 단일 가우시안 확률 밀도함수로 모델링 가능

- 여러개의 가우시안 언덕들로도 모델링 가능 => GMM 혼합 가우시안 모델

- 아래는 단일 가우시안 확률 밀도 함수와 혼합 가우시안 확률 밀도 함수의 비교

- 혼합 가우시안 확률 밀도 함수의 데이터 분포

통계학과 확률 밀도함수 추정

- 통계학적 기법으로 샘플 데이터들로부터 그들을 가장 잘 표현하는 평균, 분산 파라미터를 추정 가능

=> 데이터가 2차원(2변수)의 경우 3차원 공간상에서 만들어짐

우도비 검증 LRT : Likelihood Test 개요

- 남자와 여자에 대한 데이터로 이루어진 2변수 샘플 데이터가 존재한다고할때 각 변수에 대한 가우시안 확률 밀도 함수는 아래와 같이 표기할수 있다.

- 두 확률 밀도 함수로 3차원 공간상이 만들어지고, 이 공간 상 한 점이 여자보다 남자 언덕에서 더 위에 위치한다면

 => 이 샘플 데이터는 여자보다 남자일 가능성이 크다

 * 아래의 경우 점 a는 여성일 확률이 p(f) = 0.15, 남성일 확률은 p(m) = 0.5로 남성일 확률이 크다.

우도비 검증 정리

- 특징 벡터 x가 주어질때, x가 속한 클래스 omega_i를 결정하자.

클래스가 2개인 문제에서 우도비 검증

- 사후확률이 더 큰 쪽의 클래스를 선정

- 다듬으면

- 베이즈 정리를 사용하면

- 정규자 p(x)를 제거하고, 우도비(liklihood ratio)에 대해서 결정 규칙 정리

 => 우도비 검증 LRT Likelihood Ratio Test

우도비 검증 결정 규칙 유도 예제 1

- 아래와 같이 두 클래스를 알때, 특징 벡터 x에 대한 아래의 우도비 함수가 주어진다.

 => 우도비 검증 결정 규칙을 찾자 (조건 : 사전 확률은 같음)

1.  LRT 식에 우도와 사전확률 대입하고 정리

2. 부호 바꾸고 자연 로그 취하자

4. 정리하면, x가 7보다 크면 omega_1에 속하고, 작으면 omega_2에 속한다

5. 그림으로 그리면

우도비 검증 결정 규칙 유도 예제 2

- 위와 우도가 같으나, 사전 확률이 5P(omega_1) = P(omega_2)일때 LRT 결정 규칙은?

 => 조금 오른쪽으로 이동했다.

-

1. 정규 분포를 따르는 임의의 수 생성

clc;
clear all;


% 균일 분포를 따르는 임의의 수 생성
% randn(p, q)
% p : 생성할 데이터 행의 갯수, q: 생성할 데이터 열의 갯수
p = 5;
q = 5;

X = randn(p, q)

2. 평균과 공분산이 주어질때. 가우시안 임의의 수 Y를 생성하기(구형 과정의 경우)

- 아래의 식을 만족하게 만들면됨

- 샘플 데이터 집합 X = {x1, ..., xn}으로 구성, 샘플 데이터 갯수 N = 10000

- 평균과 공분산이 아래와 같이 주어질때 결과

 * 공분산은 각 차원에서의 분산값이 모두 8000인 구형 확률 과정

- Y(1:10, : ) => 1~ 10번째 샘플 데이터 출력

- scatter 함수로 1~ 500번째까지 샘플데이터 산점도로 출력

   => 평균 730, 1090을 중심으로 샘플 데이터가 구형 분포됨을 볼수 있음.

clc;
clear all;

N = 10000;
mu = [730, 1090]
sigma1 = [8000 0;0 8000];

X = randn(N, 2);
Y = X * sqrtm(sigma1) + repmat(mu, N, 1);

Y(1:10, :)
scatter(Y(1:500,1), Y(1:500,2));
grid on
axis tight

2. 대각 공분산인 경우

- 대각 공분산 성분만 존재하는 경우. 기울어짐 없이 데이터 축과 평행

clc;
clear all;

N = 10000;
mu = [730, 1090]
sigma1 = [8000 0;0 18500];

X = randn(N, 2);
Y = X * sqrtm(sigma1) + repmat(mu, N, 1);

Y(1:10, :)
scatter(Y(1:1000,1), Y(1:1000,2));
grid on
axis equal

3. 완전 공분산 행렬의 경우

- 축과 평행한 대각 공분산 행렬과 달리 한쪽 방향으로 기울어짐이 존재

 => 확률 변수간 상관관계가 존재. x1이 조금변할때 x2가 크게 변함

clc;
clear all;

N = 10000;
mu = [730, 1090]
sigma1 = [8000 8400;8400 18500];

X = randn(N, 2);
Y = X * sqrtm(sigma1) + repmat(mu, N, 1);

Y(1:10, :)
scatter(Y(1:1000,1), Y(1:1000,2));
grid on
axis equal

구형 공분산 가우시안 Sphere Covariance Gaussian

- 공분산 행렬이 아래와같이 분산 * 단위행렬의 경우

- 확률 밀도 함수로 구하기 위해 D + 1개의 파라미터가 필요하며, mu와 스칼라 분산은 아래와 같이 추정

 * 표본 평균 hat{mu}와 각 차원별 분산값 hat{sigma^2} => 표본 평균 1개 + 분산값 D개.

 => 구형 공분산 가우시안을 모델링하기 위해선 D + 1개의 파라미터가 있으면 수학적 모델링 가능.

   + 데이터가 적고, 계산속도도 빠르고 유용함

대각 공분산 가우시안 Diagonal Covariance Gaussain

- 공분산 행렬 Sigma가 대각 행렬인 경우, 확률 밀도 함수 모델을 하기위해선 2D차원의 파라미터들이 필요

- 각 차원별 표본 분산 hat{sigma_i}와 표본 평균 hat{mu_i} => 표본 분산(D)개 + 표본 평균(D)개 = 2D

 -> 데이터가 축에 평형하게 타원 분포.

 => 특징들간의 상관 관계는 무시함

 => but. 학습 데이터와 모델링 성능 사이 절충. 혼합 모델 사용시 유용

완전 공분산 가우시안 형태 full covariacne gaussian

- 공분산 행렬 Sigma가 아래와 같이 완전 공분산 행렬인 경우

- 완전한 확률 밀도 함수 모델링 하기 위해서 D + D(D+1)/2개의 파라미터 필요

- 학습 데이터로 mu와 Sigma 추정가능

- 완전 공분산 가우시안 형태를 사용하지 않는 이유

 => 특이 행렬 singular matrix이 되어 역행렬을 계산할수 없을 수 있음. sphere 타입 만으로도 충분한 성능을 보임

복습) 특이행렬과 비특이 행렬, 랭크

- 행렬 A가 주어질떄

- 특이 행렬 : A의 랭크가 행/열 길이보다 작은 경우

- 비특이 행렬 non singular matrix : 행렬 A의 랭크가 행/열 길이와 같은 경우

* rank(A) : 행렬 A의 행(열)벡터가 선형 독립인 경우의 갯수. 행이 m개라고 m개다 선형독립이 아닐수 있음.

단변수 가우시안 분포 univariate(unimodal) gaussian distribution

- 가장 많이 사용하는 분포

- 두 개의 파라미터(모수) 평균 mu와 표준편차 sigma가 사용됨.

- 아래의 식은 단변수 가우시안 분포의 확률 밀도 함수

 => 파라미터인 모집단의 평균 mu과 분산 sigma를 알면 확률 밀도 함수로 모델링 가능! 

- 단변수 가우시안 분포의 예시

 * unimodal은 단봉. 즉, 봉우리가 하나인 가우시안 분포를 의미함.

이변수 가우시안 분포 bivariate guassian distribution

- 확률 변수가 1변수가 아닌 2개인 경우 가우시안 분포

다변수 가우시안 분포 multivariate guassian distribution

- 벡터공간 R^n에서 정의됨. 

- 평균 mu와 공분산 Sigma는 n x n 크기의 가역적인 양의 정부호 행렬 invertible positive definite 대칭 행렬

- 여기서 mu는 가우시안들의 중심으로 (d x 1) 형태의 벡터

- sigma는 (d x d) 형태의 공분산 행렬)

- 아래의 그림은 이변수 인 경우의 다변수 가우시안 분포의 공분산 형태에 따른 확률 분포 플로팅 결과를 보여줌

복습 정리 : 선형대수(복) - 4. 고유치와 대각화, 변환, 분해

복습) 양의 정부호 행렬, 양의 준정부호 행렬

- 행렬 A가 주어질때, 벡터 x가 0이외인 경우에도 아래의 조건을 만족하면 A는 양의 (준)정부호 행렬이 됨.

- 양의 정부호 행렬 positive definite matrix : x^T A x >= 0

- 양의 준정부호 행렬 positive semi-definite matrix :  x^T A x X 0

복습) 양의 정부호 행렬과 직교화

- 조건 1. A가 양의 정부호 행렬이고, x가 직교 행렬인 경우

    * x x^T = I 가 성립하는 경우 -> x^-1 = x^T인 경우 x는 직교행렬)

- 조건 2. 아래를 만족하는 대각 행렬 x가 존재할때, A는 대각화가 가능함 diagonalizable

     D = x^-1 A x

- 정리 : 위 두 조건에 따라 다음의 고유치 분해 eigen value decomposition 를 위한 식을 얻을수 있음

     D = x^T A x

  => 결론 : 역행렬 x^-1 계산 없이 전치행렬 x^T로 행렬 A는 대각화 가능함 -> 고유치 분해

중심 극한 정리 central limit theorem

- 표본 크기 n이 증가할수록, 표본 평균은 정규분포에 까워짐

=> 즉, 표본의 크기가 증가할수록 모집단의 평균과 분포와 유사해짐

- 아래의 그림은 표본의 갯수가 커질수록, 확률 분포가 정규 분포와 유사해지는 과정을 보여주고 있음.

벡터 확률 변수, 벡터 랜덤 변수 vector random variable

- 확률 변수가 2개 이상인 경우 -> 벡터 랜덤 변수 or 벡터 확률 변수라 함

- 기존의 1변수 확률 변수를 길이가 2이상인 열 벡터로 정의

* 그냥 다변수 확률 변수라 하겠다.

결합 확률 밀도 함수 joint pdf

- 다변수 확률 분포를 따르는 확률

 * 결합 확률이란? 여러개의 확률 변수들이 결합된 경우의 확률

- 아래의 그림은 변수가 2개인 결합 확률 밀도 함수로 평면에 대한 확률을 보여줌

- 이변수 표준 정규 분포의 경우 확률 밀도 함수를 3차원 플로팅 시킨 결과

- 1변수 확률 밀도 함수는 아래와 같이 직선에 대한 확률로 나타낸다.

결합 누적 분포 함수 joint cdf

- 다변수 확률 분포를 따르는 누적 확률

- 확률 변수 X, Y가 주어질때 결합 누적 확률 분포 함수 F는 아래와 같음.

다변수 확률 변수(랜덤 벡터 확률변수)의 통계적 특징

- 일변수 확률변수(스칼라 확률변수)와 동일하게 정의

공분산 행렬

- 다변수 확률 변수에서 확류변수들간에 퍼진(영향)의 정도

- 다음의 공분산 행렬이 주어질때, 2변수 확률분포 표본 데이터들의 분포

- 위 공분산 행렬의 고유치와 고유벡터

확률 변수 random variable

- 실행 결과들을 수치로 대응시키는 함수

 * 확률 변수는 변수 variable이 아니라 하나의 실수 함수(real function)

확률 변수의 예시

- 두개의 동전을 동시에 던지는 실험

 => 확률변수 X에 사용가능한 x = {0, 1, 2}

확률 분포

- 확률 변수 개별 값들의 분포

- P(X = x)로 정리하면 확률분포표를얻을수 있음.

=> 확률 함수 : 개별적인 확률 값들을 확률 공간상의 확률로 정리하는 함수

확률 함수의 종류

- 이산 확률 분포 : 확률 변수가 이산 확률변수인 경우. => 확률 질량 함수 PMF Probability Mass Function

- 연속 확률 분포 : 확률 변수가 연속 확률변수인 경우 => 확률 밀도 함수 PDF Probabilty Density Function

- 누적 분포 함수 CDF cumulative Distribution Function

  : 확률 질량/밀도 함수를 누적하여 얻은 확률변수

 => 아래는 정규분포의 누적 분포 함수

확률밀도함수와 확률 질량함수

- 확률 밀도함수 : 연속확률변수 X의 누적확률분포 F(X)의 미분으로 정의

- 확률 질량함수 : 이산확률변수 X의 누적확률분포 F(X)의 미분으로 정의

기대값 Expectation

- 학률변수의 평균

- 표본 성질 : 일반 데이터들의 성질

- 확률 분포의 성질 : 모집단(or 모델)의 성질 

 * 기호구분 : 일반 데이터(샘플, 표본)와 모집단(전체 집단)의 평균과 표준 편차 기호를 아래와 같이 구분함

표본 기댓값 expectation of sample 과 모집단 기댓값 expectation of population

- 샘플 데이터들의 평균은 아래의 식으로 계산.

- n_x를 x의 횟수라 한다면, 아래와 같이 정리되고 n이 커지면 통계적 확률(근사 확률 ) p(x)를 얻음

 => n이 전체 공간의 갯수만큼 된다면 모집단의 평균을 구하게 됨.

표본에 대한 분산으로 모집단 분산 구하기

- 표본에 대한 분산 식이 주어지면 아래의 정리를 통해 n이 최대가 되면 모집단의 분산이 됨.

통계적 현상 statistical phenomena

- 여러번 관찰해서 법칙을 찾아낼수 있는 현상

확률 실험

- 반복 할수록 규칙성이 존재하는 행위

확률

- 특정 현상이 확실히 발생할 정도

확률 법칙

- 임의의 실험에서 사건에 확률을 배정하는 규칙

수학적 확률

- 표본 공간 S과 S를 구성하는 사건 A가 있을때, 다음의 P(A)를 수학적 확률

 * 수학적 확률은 각 사건들이 일어날 가능성이 모두 동일하다고 가정

 * 동전 2개를 던질때 앞면이 0개, 1개, 2개가 나올 확률을 다 동일하게 1/3, 1/3, 1/3이라고 가정하면 안됨.

통계적 확률

- 동일한 현상이 일어날지 불확실한 경우, 여러번 실험해서 얻은 사건에 대한 확률은 상대적인 횟수로 추정

- 상대적인 횟수 relative frequency는 n번 실험할때 r회 일어난 경우 r/n.

 * 동전 2개를 던질때 앞면이 0개, 1개, 2개가 나올 (통계적) 확률은 1/4, 1/2, 1/4

수학적 확률과 통계적 확률의 차이

- 수학적 확률은 표본 공간을 구성하는 사건들이 동일한 확률을 가지고 있다고 생각

- 통계적 확률은 여러번 반복했을때 나온 정도(상대적 횟수)로 확률을 추정

통계적 확률 정리

- n회 실험 할때, A의 상대 횟수 r/n이 특정한 수 p에 수렴하는 경우 => 통계적 확률

- 정확한 p 값은 알수 없으나, n이 충분히 크다면 근사적으로 상대 도수를 통계적 확률로 본다.

표본 공간 sample space과 확률 공간 probability space

- 표본 공간 : 관측으로 얻은 결과 집합

- 사건 : 표본 공간의 부분 집합

- 확률 공간 : 표본 공간을 확률에 대응시킨 결과 집합

주변 확률과 조건부 확률

- 주변 확률 marginal probability : 두 사건 A, B가 존재할때, A나 B 한 가지의 사건만 일어날 확률

- 조건부 확률 conditional probability : 두 사건 A, B가 발생 했는데, B의 확률을 알때 A가 일어날 확률

전체 확률 이론 total probability thorem

- 사건 A들의 합집합이 표본 공간이고, 서로 배타적일때 사건 B는 다음의 그림과 같이 구성됨.

- 사건 B의 확률은 B와 사건 A들의 교집합들의 합

귀납적 추론과 연역적 추론

- 통계학은 대부분의 경우 표본에서 모집단을 추정

 => 귀납적 추론 inductive inference : 개발적 사건으로 일반적 법칙 유도

- 연역적 추론 deductive inference : 일반적 법칙으로 개별적인 사건 유도

베이즈 정리 bayes thorem

- 일반적인 법칙을 알수 없는 불확실한 상황에서 의사 결정 문제를 다룰때 중요하게 사용됨

- (연역적 추론 방식인) 확률로 (일반적인 법칙을 유도하는) 귀납적 추론 방식을 행하는 행위

베이즈 정리와 확률의 의미

- 기존의 확률 : 직접 확률 direct probability

- 베이즈 정리 : 역확률 inverse probability

베이즈 법칙(정리?)로 정리하기

- 표본 공간 S와 분할 영역 A들이 주어질때, B가 난 경우 A_i에서 일어날 확률이 얼마나 될까?

- 조건부 확률 conditional probability 을 전체 확률 정리 total probability thorem으로 정리하면

 => 사건 B가 발생했을때 A_i가 일어날 확률을 알고 싶으나 모르는 경우

    사건 A_i가 일어났을때 B가 일어날 확률을 안다면 구할수 있다.

* 개별적 사건에 대한 확률로 일반적인 법칙을 추론해냈다?

통계적 패턴인식에서의 베이즈 정리

- 특징 벡터 x가 관측되었을때 클래스 omega_i를 찾자. P(omega_j | x) = ?

 => p(x | omega_i)를 알면 구할수 있다. (클래스가 주어질때, 특징 벡터 관측에 대한 조건부 확률)

- 베이즈 정리 : 우도를 알때 사후 확률을 구하는 정리

베이즈 정리 용어 정리

- 사전 확률 priori probability : P(omega_1). 클래스 omega_1의 확률

- 정규화 상수 : p(x), x 확률 결정에 영향을 주지않는 정규화 상수

- p(omega_1 교집합 x ) = 1/10 (임의로 정의)

- 우도 likelihood : 클래스 omega_i가 주어질때, 관측 x이 일어날 확률

- 사후 확률 posterior probaility : 관측 x이 있을때, 클래스 omega_1에 속할 확률

 => 특징 벡터 x가 관측되었을때, 분류한 결과가 omega_1일 확률은 0.3

 => 특징 벡터 x는 30%의 확률로 omega_1로 분류된다!!