지난번 그래프 정리 글에서 그래프에 관련한 기본적인 이론과 활용 예시 들을 간단하게 살펴보았고,
ref : throwexception.tistory.com/1185
이번에는 그래프의 역사적인 배경과 다양한 문제들, 그래프 탐색 등에 대해 알아보자.
1. 그래프 이론의 시작 : 쾨니흐스베르크의 다리
- 오일러가 1736년에 쓴 쾨니히스베르크의 다리 문제에 대한 논문에서부터 시작됨
- 질문 : 프로이센 쾨니히스베르크에는 다리가 7개가 있는데, 모든 다리를 한 번씩만 건너서 모두 지나갈수 있을까?
- 아래의 그림은 쾨니히스베르크의 지도
https://ko.wikipedia.org/wiki/%EA%B7%B8%EB%9E%98%ED%94%84_%EC%9D%B4%EB%A1%A0
2. 오일러 경로 Eulerian Path
- 오일러는 강으로 나눠지는 육지들을 A ~ D라고 이름을 주고, 각 다리마다 a ~ g라는 이름으로
- 여기서 A ~ D는 노드/정점이며, a ~ g 에지/간선이 된다.
- 아래의 그림은 오일러가 1736년 발표한 논문에서의 다리 스캐치
https://suhak.tistory.com/54
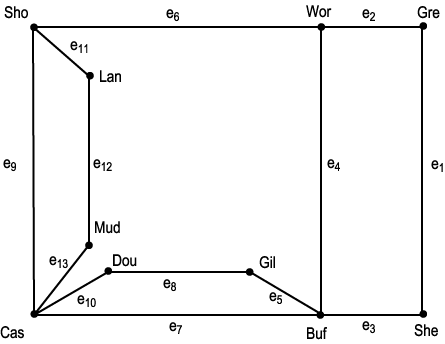
- 아래의 그림은 쾨니히스베르크의 다리를 그래프로 나타낸 결과물
- 오일러는 정점/노드가 짝수개의 차수를 갖는다면 모든 다리를 한번씩 건너는게 가능하다고 정리
* 오일러 경로 : 유한 그래프 Finite Graph의 모든 에지/간선를 한번씩 통과 하는 경로(한붓 그리기)
=> 쾨니히스베르크의 다리는 정점 갯수가 짝수 개의 차수가 아니므로 오일러 경로가 아니다/한붓 그리기가 안된다.
https://steemit.com/kr-science/@rubymaker/tb24i-rubymaker
3. 해밀턴 경로 Hamilton path
3.1 해밀턴 경로 개요
- 그래프이론에서 오일러 경로와 비슷한 경로로 해밀턴 경로가 있다.
- 해밀턴 경로 : 모든 정점을 한번씩 방문하는 그래프 경로
* 오일러 경로는 모든 에지를 한번씩 방문 한다면, 해밀턴 경로는 모든 정점을 한번씩 방문 해야함.
- 해밀턴 경로 찾기 -> 최적 알고리즘이 없는 NP-완전/NP-complete 문제
ref : ko.wikipedia.org/wiki/%ED%95%B4%EB%B0%80%ED%84%B4_%EA%B2%BD%EB%A1%9C
* 오일러경로와 해밀턴 경로의 비교
http://nogwon.blogspot.com/2013/12/blog-post_7760.html
* 입체 도형의 해밀턴 경로들
https://blog.daum.net/sshyorim/900498
3.2 해밀턴 순환
- 해밀턴 순환 출발점으로 돌아오는 해밀턴 경로
정십이면체
정십이면체의 모든 꼭짓점을 지나는 해밀턴 순환
3.3 외판원 문제 Travelling Salesman Problem : TSP
- 각 도시를 방문하고 최단 경로를 찾는 문제
- NP-난해에 속하는 문제로, 계산 복잡도 이론에서 최적의 해를 구하기 힘든 문제의 대표적인 예시가 된다.
* 다항식 시간 내 풀수 있는 알고리즘이 없으므로 모의 담금질이나 유전 알고리즘으로 근사해를 구한다!
ref : ko.wikipedia.org/wiki/%EC%99%B8%ED%8C%90%EC%9B%90_%EB%AC%B8%EC%A0%9C
- Question : 도시가 20개인 경우, 최적의 경로를 찾으러면 얼마나 많은 경로를 다녀야 할까?
=> Answer : 20! = 2,432,902,008,176,640,000 이 중에서 가장 짧은 경로를 찾기는 힘들다.
외판원 문제의 정답
4. 복잡도와 문제들
4.1 NP 복잡도
- 비결정론적 튜링 기계 Non Deterministic Turing Machine : NTM으로 다항 시간안에 풀수 있는 판별 문제 의 집합
- NP는 Non deterministic Polynomial time의 약어
- NP에 속하는 문제들은 결정론적 튜링 기계로 다항 시간에 검증이 가능하다.
ref : ko.wikipedia.org/wiki/NP_(%EB%B3%B5%EC%9E%A1%EB%8F%84)
4.2 계산 복잡도 이론 Computational Complexity theory
- 컴퓨터 과학의 계산 이론의 한 분야로 알고리즘을 복잡도에 따라 분류한 문제의 모임을 구성
- 알고리즘 수행을 (실제 컴퓨터로도 가능하나) 튜링 기계를 이용한 방법을 사용
- 복잡도의 기준 : 시간 복잡도(알고리즘 소요 시간)와 공간 복잡도(메모리 등 자원 사용량)
=> 복잡도에는 어떤게 있을까?
https://brilliant.org/wiki/complexity-theory/
4.3 복잡도 종류
- 계산 복잡도에 따라 문제를 분류한 것
- 일반적인 정의 : 추상 기계 abstract machine이 O(f(n)) 만큼의 자원 R을 이용하여 풀수 있는 문제의 종류
- 복잡도 종류의 예시
example 1) NP : 확률적 튜링기계가 다항 시간에 풀 수 있는 판정 문제의 집합
example 2) PSPACE : 결정론적 튜링 기계가 다항 공간에서 풀 수 있는 판정 문제의 집합
ref : ko.wikipedia.org/wiki/%EB%B3%B5%EC%9E%A1%EB%8F%84_%EC%A2%85%EB%A5%98
=> 추상 기계, 튜링 기계, 판정 문제, 다항 시간, 다항 공간 란 무엇일까?
복잡도 종류 사이의 관계
4.4 추상 기계 abstract machine
- 컴퓨터 하드웨어나 소프트웨어의 이상적인 모형, 추상컴퓨터라고도 부름
- 계산 이론에서 추상 기계를 사고 실험에서 사용해, 계산 가능성이나 알고리즘 복잡도 추정
- 추상 기계를 통해 실제 컴퓨터를 만들지 않더라도 실행 시간이나 메모리 등 자원이 얼마나 필요한지 예측 가능
* 사고실험 though experiment : 가상 시나리오가 어떻게 동작하는지 생각하는 방법. 경험적 방법(관찰, 실험)과 반대됨
ref : ko.wikipedia.org/wiki/%EC%B6%94%EC%83%81_%EA%B8%B0%EA%B3%84
- 아래는 사고 실험의 예시. 이발사는 누구를 면도해야 할까?
https://fs.blog/2017/06/thought-experiment/
4.5 튜링 기계 Turing Machine
- 수학/이론 전산학에서의 튜링 머신 :계산을 할수 있는 기계를 대표하는 가상의 장치, 수학적 모형
- 1936년 튜링은 automatic의 a자를 따서 a-기계라는 이름을 붙였으나 창시자의 엘런 튜링의 이름을따 튜링 기계가 됨.
- 튜링 기계의 구성 : 무한한 길이의 테이프(저장공간)과 테이프에 정보를 쓰고 읽을 수 있는 기계, 그리고 어떻게 값을 줄지 기록하는 상태, 행동표로 구성
* 실제 컴퓨터는 CPU, GPU로 정보를 처리하고, 주/보조 기억장치로 정보를 저장
=> 튜링 머신은 실제 컴퓨터를 대신하여 사고 실험에 사용하기 위한 가상의 수학적 모형/장치
https://www.futurelearn.com/info/courses/how-computers-work/0/steps/49259
- 튜링이 말하는 튜링 머신의 정의
"무한한 저장공간은 무한한 길이의 테이프로 나타나는데 이 테이프는 하나의 기호를 인쇄할 수 있는 크기의 정사각형들로 쪼개져있다. 언제든지 기계속에는 하나의 기호가 들어가있고 이를 "읽힌 기호"라고 한다. 이 기계는 "읽힌 기호"를 바꿀 수 있는데 그 기계의 행동은 오직 읽힌 기호만이 결정한다. 테이프는 앞뒤로 움직일 수 있어서 모든 기호들은 적어도 한번씩은 기계에게 읽힐 것이다"
ref : ko.wikipedia.org/wiki/%ED%8A%9C%EB%A7%81_%EA%B8%B0%EA%B3%84
- 아래는 세 정수를 다루는 어셈블리 코드
1. EAX 레지스터(위치)에 10000h를 쓰기
2. EAX 레지스터(위치)의 값과 40000h를 더하고 쓰기
3. EAX 레지스터(위치)의 값과 20000h를 빼고 쓰기
4. 모든 레지스터를 호출
4.6 결정 문제/판정 문제 Decision Problem
- 계산이론에서의 판정 문제 : 형식 체계에서 예-아니오로 답이 있는 질문
- example 1 : 두 수 x, y가 있을때 y는 x로 나누어 떨어지는가?
- 결정 문제와 알고리즘 : 판별 문제를 푸는데 사용되는 방법이 알고리즘.
- 결정 문제를 풀 수 있는 알고리즘이 존재한다. -> 결정 가능
- 결정 문제를 풀 수 있는 알고리즘이 존재하지 않는다. -> 결정 불가능
* 결정가능성 decidability : 해답을 내놓는 기계적인 절차/알고리즘이 존재하는 성질
ref : ko.wikipedia.org/wiki/%EA%B2%B0%EC%A0%95_%EB%AC%B8%EC%A0%9C
ps. 판정 문제는 예 혹은 아니오라는 답이 존재하는 질문인데, 외판원 문제의 경우 경로같은 정답이 나온다. 복잡도 종류에서 말하는 판정 가능이란 예/아니오라는 범위를 넘어서 해답이 존재하는 문제를 말하는것 같다.
* 계산 이론에서 결정 Decision과 결정론적 deterministic이란 단어는 한글로 동일하게 결정이라 부르나 구분을 해야되는것으로 보인다.
결정 문제는 네 혹은 아니오의 출력만 가진다.
4.7 결정론적 알고리즘 deterministic algorithm
- 예측한 그대로, 생각한 그대로 동작하는 알고리즘
- 대표적인 예시로 수학에서 사용하는 함수
- 한계 : 결정론적 알고리즘을 찾기 힘든 문제가 존재한다
-> 예시 : NP-완전(실생활에 중요한 많은 문제들이 NP-완전. ex : TSP)
=> 비결정론적 알고리즘이 필요하다!
4.8 비결정론적 알고리즘 non deterministic algorithm 만들기
- 입력 이외의 외부 상태를 알고리즘에 적용
- 알고리즘이 시간에 민감하게 영향을 받도록 동작.
- 하드웨어의 오류를 반영하여 알고리즘 진행을 예상할 수 없게 한다.
=> 예상한 대로 정확하게 동작하지 않는 알고리즘
- 비결정론적 알고리즘의 한계 : 비결정론적 튜링 기계를 이용하면 쉽게 풀수 있으나, 실제 구현하지 못함.
=> NP-완전 문제들의 근사해 approxminate solution이나 특이해를 구하는게 한계
ref : ko.wikipedia.org/wiki/%EA%B2%B0%EC%A0%95%EB%A1%A0%EC%A0%81_%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
4,9 비결정론적 튜링 기계 Non deterministic Turing Machine(NTM)
- 튜링 머신에서 움직일수 있는 상태의 개수가 하나였던과 달리 움직일 수 있는 상태 갯수가 하나로 정히지지 않은 머신
- 이동 가능한 상태가 여러개 되거나 아예 없을 수 있음.
=> 기존의 컴퓨터는 쓰레드나 멀티프로세싱 등 병렬 처리 기법이 존재하지만, 모든 CPU의 연산들은 기계어까지 내려가서보면 병렬로 동작하는게 아니라 순차적으로 연산되니. 아예 병렬 연산이 가능한 기계를 말하는 것으로 보임.
결정론적 튜링기계와 비결정론적 튜링 기계 비교
ref : ko.wikipedia.org/wiki/%EB%B9%84%EA%B2%B0%EC%A0%95%EB%A1%A0%EC%A0%81_%ED%8A%9C%EB%A7%81_%EA%B8%B0%EA%B3%84
4.9 다항 시간 polynomial time과 복잡도 클래스
- 다항 시간 : T(n) = O(n^k)와 같이 다항 표현의 상한을 가지고 수행되는 알고리즘은 다항 시간 을 가진다.
P: 다항 시간동안 결정적 튜링 머신에서 해결할 수 있는 결정 문제의 복잡도 클래스
NP: 다항 시간동안 비결정적 튜링 머신에서 해결할 수 있는 결정 문제의 복잡도 클래스
ZPP: 다항 시간동안 확률적 튜링 머신에서 0의 에러확률로 해결할 수 있는 결정 문제의 복잡도 클래스
RP: 다항 시간동안 확률적 튜링 머신에서 단방향 에러를 가지고 해결할 수 있는 결정 문제의 복잡도 클래스
BPP: 다항 시간동안 확률적 튜링 머신에서 양방향 에러를 가지고 해결할 수 있는 결정 문제의 복잡도 클래스
BQP: 다항 시간 동안 양자 튜링 머신에서 양방향 에러를 가지고 해결할 수 있는 결정 문제의 복잡도 클래스
ref : ko.wikipedia.org/wiki/%EC%8B%9C%EA%B0%84_%EB%B3%B5%EC%9E%A1%EB%8F%84
=> P 문제 : 다항 시간동안 결정론적 튜링 머신으로 풀 수 있는 문제. (일반적인 알고리즘 테스트 문제들)
=> NP 문제 : 다항 시간동안 비결정론적 튜링 머신으로 푸는게 가능한 문제(P 문제를 포함함)
4.10 지금까지 본 내용들
- 계산복잡도 이론 : 알고리즘을 복잡도에 따라 어떻게 분류할지 연구하는 이론
- 판정 문제 decision problem : 실제로 해답을 찾을 수 있는 문제(해답이 존재하는 문제)
- 사고 실험 : 실제 하드웨어나 소프트웨어 없이 가상의 시나리오로 어떤 결과가 나오는지 다루는 실험.
- 튜링 머신 : 사고 실험에 사용하기 위한 가상의 장치. 실제 컴퓨터로 구현됨.
- 비결정론적 튜링 머신 NTM : 여러 상태를 동시에 처리 가능한 튜링 머신, 병렬 처리 가능한 가상 기계
- 결정론적 알고리즘 : 예측한 대로 동작하는 알고리즘. ex) 수학 함수
- 비결정론적 알고리즘 : 예측한대로 정확히 동작하지 않는 알고리즘. NTM으로 풀기가능 ex)NP-완전
- 다항 시간 알고리즘 : 시간 복잡도가 O(n^k)로 다항식 시간인 알고리즘.
=> 아래의 그림을 참고하여 대표적인 문제들을 살펴보자.
복잡도 종류 사이의 관계
4.11 복잡도 정리
- EXPSPACE : 결정론적 튜링 기계가 O(2^{p(n)}) 공간 으로 풀수 있는 판정 문제 집합. p(n)은 n에대한 다항함수
- EXPTIME : 결정론적 튜링 기계가 O(2^{p(n)}) 시간 에 풀수 있는 모든 판정 문제 집합. p(n)엔 n에대한 다항함수
- PSPACE : 결정론/비결정론적 튜링기계가 시간에 상관없이, 다항 공간 을 써서 풀수 있는 판정 문제 집합
- NP : 비결정론적 튜링기계 NTM으로 다항시간 에 풀수 있는 판정 문제 집합.
- NP-HARD : 적어도 모든 NP 문제만큼 어려운 문제들의 집합
* NP는 NTM으로 다항식 시간에 풀수 있는 문제 집합, NP-hard는 NP만큼이나 어려운 문제 집합점에서 다름
* NP-Hard 중에서 NP에 속하지 않은 문제들이 존재
- NP-Complete : NP-HARD이지만, NP로 바꿀수 있는 문제 집합
- P(PTIME) : 결정론적 튜링 기계로 다항 시간 안에 풀수 있는 판정 문제 집합.
P 문제와 NP완전은 NP 문제들의 부분집합
NP 문제와 NP완전의 관계
4.11. 해밀턴 경로와 외판원 문제를 계산 복집도 이론으로 보기
4.11.1 해밀턴 경로 문제와 외판원 문제의 관계
- 해밀턴 경로 : 한 번만 방문하는 경로
- 해밀턴 순환 : 한 번만 방문하여 출발지로 돌아오는 경로
- 외판원 문제 : 한 번만 방문하여 출발지로 돌아오는 경로 중가장 짧은 분류
=> 해밀턴 경로 > 해밀턴 순환 > 외판원 문제
4.11.2 문제 정의
문제 1. 해밀턴 경로가 존재하는가?
문제 2. 각 도시를 방문하고, 돌아오는 가장 짧은 경로 찾아라(최단거리 해밀턴 순환 찾기)
4.11.3 문제 1번 보기
- 질문 : 해밀턴 경로가 존재하는가?
- 예/아니오로 대답할 수 있는 결정 문제이며, 다항 시간에 검증이 가능한 NP 문제이며, NP-Hard -> NP-완전
4.11.4 문제 2번 보기
- 질문 : 각 도시를 방문하고 돌아오는 가장 짧은 경로를 찾아라
- 예/아니오로 대답할 수 있는 결정 문제가 아니므로, NP 문제가 아닐 수 있다.
- 증명된 NP-난해 문제이나 NP 문제가 아닐수 있어 NP-완전 문제가아니며, NP-난해
5. 그래프 순회 Graph Traversals, 그래프 탐색 Graph Search
5.1 그래프 탐색 개요
- 그래프 순회/탐색은 그래프가 가지고 있는 정점들을 방문하는 것을 말함.
- 대표적인 그래프 탐색 방법으로 깊이 우선 탐색 Depth First Search DFS와 너비 우선 탐색 Breadth First Search BFS
* 위와 같은 기본적인 그래프 탐색 알고리즘에서 최적 탐색 방법과 경험적 탐색 방법을 활용하여 개선된 방법들이 존재
임의 경로 탐색
최적 경로 탐색
맹목적 탐색 blind search 깊이 우선 탐색 Depth First Search 너비 우선 탐색 Breadth First Search 균일 비용 탐색 Uniform Cost Search
경험적 탐색 heuristic search 언덕 오르기 탐색 hill Climbing Search 최적 우선 탐색 다익스트라 알고리즘 Dijkstra algorithm A* 알고리즘 Astar Algorithm
5.2 깊이 우선 탐색과 너비 우선 탐색
- DFS는 왼쪽 깊이 방향을 우선으로 탐색
- BFS는 너비 방향을 우선으로 탐색
https://medium.com/@kenny.hom27/breadth-first-vs-depth-first-tree-traversal-in-javascript-48df2ebfc6d1
5.3 백트래킹 BackTracking
- 탐색을 하다가 진행 할 수 없을때(후보 경로를 포기) 왔던 길을 되돌아서 탐색을 진행하는 것에서 유례
- DFS 같은 방식으로 탐색하는 모든 방법을 의미, 주로 재귀로 구현하며 기본적으로 DFS에 속함.
- 최적의 경우 적은 시행착오로 목표 도달하나 최악의 경우 모든 경우를 고려해야함
* 브루트 포스와 다른 점은 가능성이 없는 경우 후보를 즉시 포기해서 되돌아간다는 점에서 개선됨.(가지치기)
ref : en.wikipedia.org/wiki/Backtracking
5.4 백트래킹과 제약충족 문제 Constraint Satisfaction Problems(CSP)
- 제약 충족 문제 : 제약 조건 Constraints를 충족하는 상태 States를 찾아내는 수학 문제.
- CSP의 예시 : 스도쿠, 십자말풀이, 퍼즐 문제, 문자열 파싱 등
- 제약 충족 문제를 푸는데 (가지치기로 최적화) 백트래킹이 필수적임.
ref : en.wikipedia.org/wiki/Constraint_satisfaction_problem
백트래킹으로 스도쿠 풀기