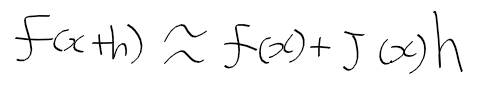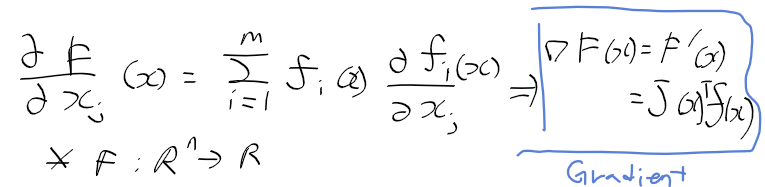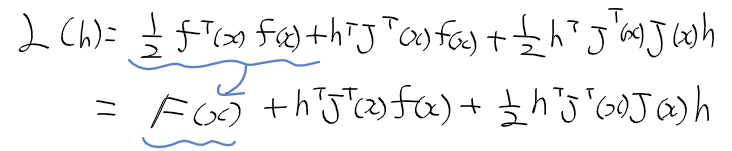집밖은 위험해

이미지 획득에서 카메라와 눈 비교

핀홀 카메라 모델

- 카메라가 영상을 얻는 원리를 간단하게 나타낸 수학적 모델

- 빛이 핀홀 카메라의 작은 구멍으로 들어가 이미지 평면, CCD 상에 맺힘

 => 빛 통과 -> 샘플링 -> 양자화 -> 디지털 영상

영상의 표현

- 2차원 행렬로 표현 -> f(x, y)

- 픽셀 : 영상의 한 점

- 해상도 : 영상의 크기

- 흑백 영상 : 명암만으로 표현하는 영상(0 ~ 255)

- 컬러 영상 : R채널, G 채널, B채널을 동시에 나타내는 영상

히스토그램

- 각 명암 값들의 빈도수를 정리한 그래프

- 히스토그램이 좌측(0)에 치우쳐지면 어둡고, 우측(255)에 치우쳐지면 밝은 영상

히스토그램 평활화 histogram equalization

- 한쪽으로 치중된 명암을 균일하게 해주는 연산

- 좌측 영상이 원본, 우측 영상이 히스토그램 평활화 수행 후 영상

히스토그램 역투영 histogram backprojection

- 특정 색상 분포 만으로 물체를 검출하는 방법 -> 명암이 아니라 색상 공간을 사용

- 히스토그램 역투영을 이용한 얼굴 검출

 1. 얼굴 모델의 색상에 큰 가중치를 주고, 나머지 영역들은 낮춤

 2. 얼굴 모델과 비슷한 영역들만 밝고 나머지는 어두워짐

영상 처리 응용 분야

- 자율 주행

- 수술 로봇

- 군사 로봇

- 탐사선 등

영상 처리 목표

1. 사람과 비슷한 인공 시각

- 어느 영상이든 사람의 인지능력을 사용하는 것 처럼 컴퓨터가 모방

 => 학습, 추론 등 인공지능 관련 문제가 해결되지 않는 이상 불가능

* 영상 처리의 어려움

- 역문제 : 입력 영상은 3차원 공간을 2차원으로 투영한 것. 영상 처리는 2차원 영상에서 3차원 공간을 이해해야함

 => 사람은 영상으로 공간 정보를 추론 할수 있으나 컴퓨터는 힘듬

- 불량 문제 : 답이 유일하지 않음 -> 영역 분할시 답이 다양함

- 변형 발생 : 기하학적 변환, 광도 변환 등이 동시에 발생

- 잡음

2. 특정 용도의 인공 시각
- 번호판 검출의 경우 : 직사각형 모양 찾기, 글자 인식

 => 사람의 인지 기능을 가진 인공 시각보다는 쉬움

컴퓨터 비전 처리 프로세스

1. 입력 영상

----------------------------------- 저급 영상 ---------------------------------

2. 전처리(영상처리) : 입력 영상을 목적에 알맞게 변환. ex) 노이즈 제거

3. 특징추출 feature extraction

 - 특징 : 에지, 선분, 원, 코너, 텍스처 -> 이들로 특징 벡터 만듬

 - 사용 특징 예시 : 얼굴 인식(Haar like), 사람 탐지(Histogram Of Gradient), 물체 인식 및 추적(SURF)

----------------------------------- 저급 영상 ---------------------------------

----------------------------------- 고급 영상 ---------------------------------

4. 해석

- 인식 : classification 수행

- 자율 주행 : 주행 방향 안내

* 데이터 베이스 생성 -> 분류기 학습 -> 후처리 -> 성능 개선

----------------------------------- 고급 영상 ---------------------------------

5. 고급 묘사

자료구조

- 기본 : 배열, 트리, 그래프

- 속도 개선 목적 : 힙, 해싱, 탐색 트리 

- 추출 특징 및 기하학 요소 : 벡터, 행렬

활용 알고리즘

- 탐욕 방법, 동적 프로그래밍, 한정 분기

- 고속 매칭 : kd트리, 해싱 활용

수학적 기반

- 선형 대수 : 행렬 연산

- 미분 : 변화크기 측정

- 확률 : 의사 결정 및 분류

문제 풀이과정

1. 최적화 문제로 정리

- 비용 함수 정의

2. 수치적 방법으로 최적회 찾음

기계 학습 도구

- Neural Network, SVM, Adaboost, Markov Random Field

설계 과정

1. 문제 파악

- 문제를 풀기 위해 제약과 범위 설정 필요

- 얼굴 인식의 경우 : 정면만? 옆면도?

2. DB 수집

- 얼굴 인식기의 경우 얼굴 데이터베이스 구축 필요

- 예시

    PASCAL VOC : 물체 인식 성능 데이터베이스 제공, 물체 종류와 위치 표시 

    버클리 데이터베이스 : 차량 번호판 글씨 제공

3. 알고리즘 설계, 구현

- 환경, 제약에 따라 결과 변화가 심함

- 많은 알고리즘 개발 -> 문제에 적절한 알고리즘을 선정 필요

 => 손찾기 : 손 모델 매칭, 지역 특징 활용, 영역 분할 아고리즘 등 다양한 경우의 수 사용 가능

* 좋은 알고리즘 찾는 방법

 - 다양한 알고리즘을 사용해봄 -> 휴리스틱.

 - 통찰 + 경험을 통해 시행착오 줄일 수 있음

 - 데이터베이스와 성능 지표로 여러 알고리즘 성능 비교

4. 성능 평가

 - TP True Positive 참 긍정 

 - TN True Negative 참 거짓

 - FP False Positive 부정 긍정

 - FN False Negative 부정 거짓

 - 정확률 precision : TP/(TP + FP) -> 찾은것(TP, FP) 중에 올바른것(TP) 비율

 - 재현율 recall : TP/(TP + FN) -> 찾아야하는 것(TP, FN)들 중에서 맞게 찾은(TP) 비율

 - 강건함 robust : 환경 변화에도 성능을 유지하는 정도

학문 분류

- 영상 처리 : 입력 영상을 노이즈 제거나 왜곡 개선 등 적합하게 처리

- 컴퓨터 그래픽스 : 고급 정보로 새 영상 생성, 합성

- 컴퓨터 비전 : 입력 영상을 분석하여 고급 정보 출력

- 패턴 인식 : 특징 추출기로 특징 추출 -> 특징 벡터 생성, 분류기로 특징 벡터를 분류

간혹 어떤 걸 공부해야지 하고 열심히 할것 처럼 말해놓고

금방 포기하는 경우가 많다.

이전에는 왜 그런지 전혀 몰랐지만

점점 공부하면 할수록 명확하게 이유를 알것 같다.

일단 첫째는 처음부터 목표를 크게 정한 점과

둘째는 기반 지식에 대해 충분히 학습하지 않은 점이 있어보인다.

아무것도 모르는 상태에서

확률적 로봇 공학을 배울때

앞의 확률 내용 1,2장만도 이해 못해서

몇달간 해멘적이 있었다.

이 외에도 컴파일이나 버전 의존 관계같은것도 몰라 오픈소스 하나 빌드하는데 오랜 시간을 소비하거나

그래프 슬램에서 그래프가 무엇인지 뉴턴 방법이 무엇인지 분명 논문 자료에 서술은 되어있지만

이해하지 못한 채 대충 넘기면서 겨우 읽었다.

이렇게 될수 밖에 없는건

확률에 대해서 시간없다고 

빌드에 대해서도 제대로 공부 하지 않았으며,

자료구조와 최적화는 물론 공업수학을 보지 않았기 때문이었다.

이런 내용을 한번 혹은 충분히 보지 않은 상태에서

확률 로봇 공학이나 슬램, 빌드 시스템에 대해서 한번에 이해하는건

욕심이었던것 같다.

조금만 더하면 해결될것 같아 미련 버리지 못하고 계속 붙잡고 있던게 몇 주 몇달이 되더라

그러다 보니 최근 공부 방식은

어느 분야를 공부하기 전에 어느정도 볼지 목표를 정하고,

특히 필요하지만 나중에 볼 부분을 잘 구분해서 빠른 시간에 훑어보았다.

어느 분야든 필요하지만, 모든 부분을 보다가는 시간 소요도 크고 이해하는데 너무 오랜 시간이 걸리고

오히려 한번 다 훑고 나서 좀 쉰 뒤에 다시보면 금방 이해되는 경우들도 많았다.

가능한 현실적인 목표를 설정해서

기반 지식만 잘 준비하면

어느 응용분야든 무작정 시작하기 보다는 조금이라도 수월하게 배울수 있었다.

특히 최적화 공부할때 많이 도움되었다.

중간 중간에 하기 싫어도 복습하게 되고

대책없이 무작정 붙잡고 있는건 너무 힘든 일은 없는것같다.

그럴때마다 중간에 미련을 놓기가 정말 어려웠지만

덕분에 지금은 예전보다 조금은 능숙해졌다.

2020-07-26

• 지난 시간에는 최적화 기본 개념부터 경사 하강, 직선 탐색, 켤래 경사 방법까지 기초적인 최적화 알고리즘들을 넓게 훑어보고 간단한 예제를 통해 하강 방향으로 일정한 보폭 크기 혹은 직선 탐색으로 구한 보폭 크기로 최소자에 수렴하는 과정을 살펴보았습니다. 이후 켤래 경사 방법부터는 처음 최적화에 대해서 공부하는 만큼 자세하게 다루기는 시간도 부족하고 어렵기 때문에 가능한 얕게 살펴보았으며, 기본적인 경사 하강 방법과 켤래 경사 방법의 차이를 비교하면서 어제 학습을 마무리 하였습니다.오늘은 뉴턴 방법부터 라그랑주 승수법을 이용한 최적화 알고리즘 전반에 대해서 간단히 살펴볼 것이고 이에 앞서 고유치 고유벡터에 잠시 살펴본 후, 마지막으로 앞으로 어떻게 학습해 나갈지 정리하였습니다.
• 우선 선형대수, 최적화, 영상 처리, 인공 지능 등의 수많은 학문들을 공부할 때마다 고유치와 고유벡터라는 개념에 대해서 잠깐잠깐 보곤 했었습니다. 하지만 이 개념에 대한 정의는 알고 있지만 의미와 어떻게 활용되는지 까지는 그다지 깊이있게 학습하지 않았고 또 잊고 있었습니다. 그래서 이번 시간에 잠시 고유치와 고유벡터에 대해 간단히 살펴보았습니다. 특히나 이 개념들은 영상 처리에서 자주 사용되며, 여기서 말하는 고유라는 단어는 독일어로 영어로 바꾸면 특성이라는 말로 바꿀수 있다고 합니다. 그래서 고유치와 고유행렬은 주어진 행렬 A의 특성을 나타내는 수라고 할수 있으며, 영상 처리 분야에서 고유 벡터는 영상이 변환되어도 변하지 않는 방향, 그리고 고유 치는 영상의 크기의 배수 혹은 반대를 나타내는 수라고 합니다. 이렇게 복습함으로서 이전에도 조금씩 조금씩 보았던 내용이지만 조금 더 확실히 정리 할 수 있었습니다.
• 뉴턴 방법은 경사 하강과 별개의 최적화 알고리즘으로 경사 하강 방법이 보폭 크기에 따라 최소자까지 여러번 반복하여 수렴한다면, 뉴턴 방법은 태일러 급수를 2차까지 전개한 식을 뉴턴 함수 L(h)로 하여, 변수 h를 최소로 만들어야 합니다. 여기서 h가 뉴턴 방법의 해라고 할수 있겠습니다. 이 방법에서는 그라디언트 벡터로 양의 확정 행렬 Hf(x, y)를 구하고, 이와 다른 값들을 조합하여 뉴턴 방법의 해인 h를 구하게 됩니다. 여기서 구한 h로 여러차례 반복 없이 한번에 최소자로 이동하게 되며, 경사하강법과의 차이라고 할수 있겠습니다.
• 레벤버그 마쿼트 감쇄 뉴턴 방법은 LM 방법이라고 부르며, 기존의 뉴턴 방법에 감쇄 인자 mu를 추가시킨 방법입니다. 여기서 감쇄 인자는 이득 비율에 따라 커지거나 줄여 최소자에 멀면 mu은 줄어 빠르게 수렴하고, 최소자에 가까워지면 감쇄 인자 mu가 커지게 됩니다. LM 뉴턴 방법의 식 유도 과정과 의사 코드를 통해 어떻게 최적화 알고리즘이 감쇄 속도를 조절하면서 초소자에 수렴해나가는지 이해할 수 있었습니다. 또한 이러한 LM 뉴턴 방법에서 매 반복마다 헤시안 행렬이 계산되는 문제가 있어 여기서 근사화된 양의 확정행렬 B를 이용하는 쿼시 뉴턴 방법에 대해서 간단하게 살펴보았습니다.
• 이전까지는 f:R^n -> R인 경우를 다루었으나 f:R^n -> R^m인 비선형 시스템에서 최적화를 수행하기 위한 대표적인 방법인 비선형 최소 자승법에 대해서 알아보면서, 왜 제곱을 사용하는지와 근사해를 구하기 위한 식을 정리하고, 여기서 근사해 최소자를 구하기 위해 경사 하강법이나 뉴턴 방법이 사용되는것을 알수 있었습니다.
• 이러한 비선형 최소 자승법의 최소자를 구하기 위한 대표적인 방법으로 LM 방법이 있었는데, 이에 앞서 LM방법의 기반이 되는 가우스 뉴턴 방법에 대해서 살펴보았습니다. 가우스 뉴턴 방법은 함수 f를 2차 태일러 전개를 수행하고 이에 대한 근사식을 구하였는데 결과적으로 L(h)가 최소로 만드는 가우스 뉴턴 해 h_gn를 구하는 방법이고, 이 과정을 간단하게 정리하였습니다. 다음으로 LM 방법에 대해서 살펴보았는데, 이 방법은 가우스 뉴턴 방법에 이전에 봤던 데로 감쇄 인자 mu를 추가한 것이라 할수 있었습니다. 감쇄 인자의 크기에 따라 레벤버그 마퀴트 해 h_lm의 변화와 이득 비율 rho를 구하는 과정 그리고, 반복 정지 조건 eta값이 어떻게 정의 되는지 등을 살펴보면서 LM 방법 전반에 대해서 살펴보았습니다.
• 이번 시간에는 다양한 최적화 알고리즘들을 살펴보면서 세세한 증명과정까지는 아니지만 선형 시스템, 비선형 시스템에서 사용가능한 각 최적화 기법들의 특징들과 식 유도 과정을 간단하게 살펴보았습니다. 이 과정에서 중간 중간에 이전에 영상 처리나 패턴 인식을 할때 잠깐 봤던 개념들을 이제서야 이해할수 있었습니다. 당시에는 공업수학이나 최적화에 대한 이해도가 전혀 없었기 때문에 무슨말인지 알수 없었지만 이렇게 최적화에 대해서 알아 본 다음 다시 시도해보면 훨신 수월하게 공부할수 있을것 같습니다. 다음 시간부터는 영상 처리를 다시 복습해볼 예정입니다.

LM 방법

- LM 방법은 레벤버그, 마퀴트가 제안한 감쇄 가우스 뉴턴 방법

- 컴퓨터 비전에서 번들 조정 bundle adjustment에서 주로 사용

- 방향 벡터 h_lm을 구하기 위해 가우스 뉴턴 방법에 감쇄 인자를 추가함

LM 방법에서 방향 벡터 h_lm

- 위 감쇄 인자가 추가된 식을 정리하면

- 감쇄인자 mu가 큰 경우

- 감쇄 인자 mu가 작은 경우

- mu를 조절하기 위해 이득 비율을 이용

LM 방법에서의 정지 조건

가우스 뉴턴 방법 개요

- 비선형 최소 자승법으로 근사 해를 구하기 위해 레벤버그-마퀴트 뉴턴 방법. 즉 LM 방법을 사용할 예정

- LM 방법은 가우스 뉴턴 방법을 기반으로 함

- 가우스 뉴턴 방법은 테일러 전개 2차식에서 시작

자코비안과 그라디언트, 헤시안

- 자코비안의 요소들은 함수 f의 미분들

- 함수 F의 그라디언트

- 함수 F의 헤시안

가우스-뉴턴 방법

- 함수 f(x + h)를 l(h)로 근사화 하면

- F(x+h)에 대한 근사식은 아래와 같다.

- L(h)를 정리하면

- L(h)가 최소가 되는 h를 구하기 위해

- 이 식을 정리하면 가우스 뉴턴 알고리즘을 정리 할 수 있다.

근사해 구하기

- 다음의 다변수 함수 f와 해 q가 주어질때, 근사해 x를 구해야함

제곱의 사용

- ||f(x)||는 미분 시 잘못될수 있으므로 ||f(x)||의 제곱을 주로 사용

- 다음의 식을 주로 사용

비선형 최소자승법

- 다음의 식 F(x)을 최소로 하는 근사해 x*를 구하는 방법

 => 최소자를 구하기 위해 경사 하강법이나 뉴턴 방법이 사용됨

비선형 최소자승법 non-linear least squares 개요

- 앞서 살펴본 경사 하강법과 뉴턴 방법의 함수는 다음과 같음

- 아래의 함수 f인 다변수 함수에서는 어떻게 최소자로 찾아갈까?

다변수 함수 지역선형성 local linear

- 다음의 다변수 함수가 있을때

- 미분 가능 함수는 지역 선형으로, 자코비안 J(x)와 극소 증감벡터 h가 주어질때 아래와 같다.

국소 증감 벡터 h에 대한 식으로 정리하기

- 초기값 x0, 종료조건 eta0 등 아래의 조건이 주어질때

- h에 대해 정리하면

 => 정규 방정식 normal equation으로 구할 수 있음

정규 방정식으로 선형 최소 자승 구하기

- 선형 시스템 Ax = b가 주어질때 ||Ax - b||를 최소로 하는 벡터 x를 구하려면

 => 최소(0)인 x를 구하기 위해선 Ax - b와 A의 전치행렬에 직교해야함

- 아래와 같이 정규 방정식으로 정리할 수 있음

- 정규방정식의 좌항에 역행렬이 존재하면

- 우리의 경우. 다음의 값을 최소로 하는 지역 증감 벡터 h를 구해야하는데

- 이를 정규 방정식으로 정리하면

쿼시 뉴턴 방법 개요

- 레벤버그 마쿼트 감쇄 뉴턴 방법의 단점(매번 헤시안 행렬 계산하는)을 보완

=> Hf(x)를 근사화된 양의 확정 행렬 B로 대신함.

쿼시 뉴턴 방법

1. 쿼시뉴턴해 h_qn를 구함

2. 직선 알고리즘으로 alpha 계산

감쇄 뉴턴 방법 알고리즘 damped newton

- 경사 하강 방향으로 조금씩 이동

- 감쇄 뉴턴 알고리즘 의사 코드

LMD-Newton 방법

- Levenberg-Marquardt Type Damped Newton Method

- 최소자에서 먼 곳에서는 경사 하강법, 최소자 근처에서는 속도가 빠른 뉴턴 방법을 사용.

 -> 경사 하강법과 뉴턴 방법의 혼합

- 위 기본 감쇄 뉴턴 탐색 방법에서 이득 비율 rho에 따라 mu가 갱신됨.

 -> rho가 1에 가까우면 mu는 줄이고, rho가 멀면 mu를 키움