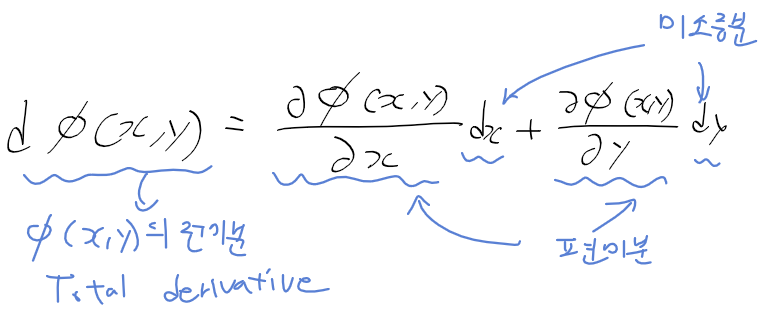집밖은 위험해

 최적화의 기본 개념

- 특정 데이터가 주어질때, 이로 부터 필요한 값들을 추출이 필요

 ex. 컴퓨터 비전, 머신러닝

- 목적 함수 objective function or 비용 함수 cost function : 이 값들을 구하기 위한 함수

최적화란?

- 목적 함수를 이용하여 f(x*) <= f(x)인 x*를 찾는 일

목적 함수의 판별 어려움

- 목적 함수로 구한 최소자가 전역 최소자인지, 목적 최소자인지 판별하기 힘듬

최소자를 찾는 방법

- 초기 지점 x0를 설정하고 초기 지점 보다 낮은 x1을 반복해서 찾음

- 하강방향 설정 -> 다음 지점 선택 -> 반복

=> 지역 최소자를 찾음

목적함수, 최소자 정리

최적화 방법들

1. 경사 하강법 gradient descent

2. 직선 탐색 line search

3. 황금 분할 탐색 gloden section search

4. 뉴턴 방법

5. 비선형 최소 자승 방법

6. 라그랑주 승수를 이용한 최적화

최소자 minimizer

- 전역 최소자 global minimizer : 함수 f : D -> R이 주어질 때, f(x*) <= f(x)인 x*

- 전역 최솟값 global minimum : 전역에대한 f(x*)

- 지역 최소자 local minimizer : 일부 구간에서 지역 최소값을 구하는 x*

- 지역 최소값 local minimum : 일부 지역에 대한 f(x*)

개구간과 폐구간

- 개구간 open interval : 초과, 미만 -> (a, b) 두 점 a, b를 포함하지 않는 사이 구간

- 폐구간 closed interval : 이상, 이하 -> [a, b] 두 점 a, b를 포함하는 구간 

컨벡스 집합 convex set

- K에 속하는 폐구간 집합

컨벡스 함수 convex function

- 컨벡스 집합 K가 주어질때 함수 f: K -> R이 아래의 조건을 따르는 함수

방향 미분 direction derivative

- 함수 f가 주어질때 하나의 방향에 대한 미분

다변수 함수에서의 평균값 정리

n차원 벡터공간에서 1차원 벡터공간에 대한 다변수 함수의 2차 테일러 급수 정리

- 연속적인 테일러 전개가 가능

m차원 벡터공간에서 n차워 벡터공간으로의 다변수 함수의 테일러 급수 정리

- n -> 1 벡터 공간과 달리 1차 테일러 전개만 가능

레벨 집합 level set

- n차원 벡터공간의 함수 f(x)가 c와 같을때에 대한 x 집합

- 벡터 공간이 2차원인 경우 레벨 집합은 등고선이 됨

곡선함수와 접선 벡터, 그라디언트

- 곡선 함수 alpha는 레벨 집합의 한 원소

- 법선 벡터 tangent vector : t0에서의 곡선 함수의 미분

- 그라디언트 벡터와 법선 벡터의 관계 : 항상 수직임

구글 상무 미키김의 세바시 영상

역사학과 출신 사회초년생이

구글에서 일하기 까지 과정을 설명하고 계신다.

당연한 이야기들이지만 가장 하기 힘든 일인듯 하다.

2020-07-21

• 지난 시간 IoT 보안 관련 내용을 학습 시작하면서 스마트 홈에서 발생하는 보안 사고들과 AI 스피커에 대한 공격 사례 그리고 어떻게 스마트홈이 구성되는지 살펴보았습니다. 이 외에 최적화 이론을 다루는데 필요한 일변수/다변수 함수에 대해서 간단하게 내용 정리를 마쳤습니다. 이번 시간에는 오픈소스 하드웨어를 활용한 AI 스피커를 활용해보고, 펌웨어와 인터페이스에 대해 그리고 데이터 시트를 보는 방법과 다양한 취약점 진단 도구들에 대해 알아봄과 동시에 실습을 진행하겠습니다. 마지막으로 최적화 이론에서 다 정리하지 못한 다양한 벡터 미분들 정리하겠습니다.
• 우선 이번에 활용해본 오픈소스 하드웨어 AI 스피커로 KT의 메이커 키트를 활용한 기가지니를 사용하였습니다. 이 키트는 라즈베리 파이를 중심으로 스피커와 마이크를 포함하여, API를 통해 기가지니 서비스를 활용할 수가 있었습니다.
• 그래서 이러한 AI 스피커와 같이 IoT 장비에서 사용하는 펌웨어와 인터페이스에 대하여 간단하게 살펴보았는데 이 때 펌웨어를 사용하는 목적과 구성 요소에 대해서 정리하고, 여기서 사용되는 JTAG과 UART와 같은 인터페이스 방식에 대해서 학습 할수 있었습니다.
• 펌웨어와 인터페이스를 살펴보는 중간에 IoT 시스템의 다양한 취약점들을 잠시 보고 지나갔었는데, IoT에서 취약점을 하드웨어와 통신, 센서, 모바일 어플리케이션 측면에서 4가지로 분류하였고 각 분류 마다 분석 깊이에 따라 확인해야할 취약점들이 어떤것들이 있는지 이해할수 있었습니다. 예를 들어 통신 취약점의 경우에는 보호되지 않는 통신 -> 입력갑 조작 -> SSL 통신 취약점 등이 있었습니다.
• 다음으로 데이터 시트 확인하는 방법을 살펴보았습니다. IoT 장비들은 다양한 개발 보드와 센서로 이루어져 있으며 이를 활용하기 위해서 데이터 시트 확인 방법의 이해가 필요하였습니다. 이전에 가장 대표적인 하드웨어 보드인 라즈베리 파이와 Atmega128 데이터 시트를 살펴본 적이 있었기 때문에 이번 시간에는 이전보다 조금 수월하게 이해할수 있었습니다.
• 데이터 시트 확인법을 살펴보고 나서 이러한 IoT 장비들의 취약점을 분석할수 있는 몇가지 도구들을 분석하였습니다. 다양한 취약점 진단 도구들이 통합된 AttifyOS부터 바이너리 이미지에서 데이터를 추출하는 Binwalk 그리고, 펌웨어 이미지를 추출하고 리빌드를 수행하는 FMK, 포트/서비스/취약점을 스캐닝 하는 Nmap, 소스 코드로부터 취약점을 정적으로 분석해주는 Yasca까지 다양한 취약점 진단 도구들이 어떤것이 있는지 알아보았습니다.
• 마지막으로 벡터 함수들을 미분한 경우들인 그라디언트와 자코비안, 헤시안 행렬들을 살펴보았습니다. 그라디언트는 벡터 함수를 하나의 변수로 미분한 것이었고, 자코비안은 벡터 함수를 다변수 1미분, 헤시안 행렬은 벡터 함수를 다변수 2미분이라 할수 있었습니다. 다양한 최적화 방법들에 있어서 이러한 벡터 함수들의 미분으로 전역 최저점으로 수렴하는 방향을 찾아낸다고 하니 수식으로 잘 정리하며 오늘 학습을 마무리 하였습니다.

2020-07-20

• 지난 시간에 선형 대수 전반의 내용을 마무리 하고 최적화를 다루기위해 1변수, 다변수, 컨벡스 함수 등의 내용들을 간단하게 살펴보았습니다. 하지만 자료 정리를 제대로 하지 못하여 이번 시간에는 스마트 홈 보안 내용을 학습함과 동시에 최적화 관련 내용들을 정리하였습니다.
• 정보 처리 기사 시험볼때 보안 이론을 일부분 학습 한 적이 있었는데, 코드를 어떻게 하면 안전하게 구현할수 있는지에 대한 방법들을 배웠었습니다. 하지만 그걸로는 부족한것 같아 IOT 관련 보안 교육을 신청하여 수강하게 되었습니다. 오늘은 IOT홈과 관련된 다양한 보안 사고들과 구성에 대해서 살펴보는 시간을 가졌습니다.
• 우선 IOT 홈이 냉장고, 에어컨, 전등, 웹캠 등 기존의 모든 가전 제품에 적용될수 잇으며 이에 사용 가능한 블루투스, 와이파이, 지그비, 로라 등 다양한 통신 방식에 대해 살펴보았고, 이러한 다양한 통신 방식중에 전력과 속도, 통신 가능 거리에 따라서 지그비 통신이 가장 많이 사용하는걸 알게 되었습니다. 이러한 집 장비들이 IOT가 되면서 다양한 보안 결함을 가지게 되어 악의적인 메일을 전송하는 봇이나 사생활 침해를 하는 도구로 활용될수 있는 위험에 대해서 들었습니다.
• 대표적으로 AI 스피커 플랫폼의 경우에 사용자의 음성을 무단으로 녹음하여 공격자에게 전달한다거나, 사용자의 음성을 녹음 후에 다시 사용하여 임의로 가정 집을 제어할수도 있는 등 AI 스피커 플랫폼을 공격하는 몇가지 시나리오에 대해서 학습하였습니다.
• 본적적으로 IOT 홈과 관련된 취약점 실습을 하기에 앞서 하드웨어 구조를 살펴보았습니다. 여기서 사용되는 라즈베리파이나 아두이노, STM, TI 사의 보드 등 다양한 개발 보드들을 살펴보고, 이러한 보드에서 사용가능한 운영체제들과 GPIO 제어, 그리고 활용가능한 센서들에 대해서 학습하였습니다. 개발 보드와 센서 간에 GPIO 제어가 이루어 지지만 중간에 존재하는 취약점들을 통해 오작동 위험성을 파악할 수 있게 되었습니다.
• 오늘은 여기까지 IOT홈에 대한 내용들을 다루었고, 다음 시간에는 AI 스피커의 활용과 펌웨어, 인터페이스 구조, 데이터 시트 확인 등 조금 더 깊이 있는 내용들을 학습할 예정입니다.
• 이후 이전에 정리하지 못하였던 1변수 함수와 다변수 함수에 대한 내용들을 다시 정리하였습니다. 1변수 함수는 한 종류의 독립변수로 이루어진 함수로, 함수는 여러개의 정의역 원소가 하나의 공역 원소에 대응하는 관계라 할 수 있었고, 일단 1변수 함수의 도함수인 상미분과 테일러 급수 정리를 살펴보았습니다.
• 1변수 함수에 대한 내용을 간단히 정리하고 나서 여러개의 독립 변수로 이루어진 다변수 함수와 이러한 다변수 함수를 행렬 형태로 표현한 이차 형식에 대해서 정리하였으며, 다변수 함수의 미분인 편미번과 전미분에 대하여 정리할 수 있었습니다.
• 다변수 함수가 주어질때 각 변수들에 대한 편미분인 그라디언트, 다변수 함수 여러개가 주어질때 각 변수들에 대한 편미분 행렬인 자코비안, 다른 변수들을 같이 미분하는 헤시안 행렬 등 기울기와 관련된 다양한 행렬 표현들의 정리를 하며 오늘 학습을 마무리 할 수 있었습니다.

벡터와 델 연산자의 내적

- 다음과 같이 벡터와 델 연산자가 주어질 때 

- 내적과 내적의 n승은 다음과 같다.

미분의 내적

- 내적의 미분을 정리하면 다음과 같다.

- 아래의 예시의 경우 행렬 형태로 구하면

헤시안 행렬 hessian matrix

기울기 벡터(그라디언트) gradient vector

- 다변수 함수에 각 변수들에 대한 편미분

자코비안 행렬 Jacobian matrix

- 아래와 같이 다변수 함수들이 주어질때

- 다변수 함수들의 변수들에 대한 편미분들의 모음 -> 자코비안

다변수 함수 multi variable function

- 독립 변수가 한개인 일변수 함수와 달리 독립 변수가 여러개 존재하는 함수

함수

- 하나 또는 여러개의 정의역 원소 (독립변수)가 하나의 공역 원소(종속변수)에 대응하는 관계

이차 형식 quadratic form

- 중간에 행렬과 앞 뒤로 두 벡터의 곱으로 이루어진 함수 형태

- 3변수, ..., n 변수 함수도 이차 형식으로 표현 가능

다변수 함수의 의미

- 다변수 함수는 보통 다음의 형태가 됨.

편미분 partial deriavative

- 1변수에서의 미분인 상미분과는 달리, 다변수 함수에서 한 변수에 대한 부분(partial)적인 미분이라 할 수 있다.

전미분 total derivative

- 함수의 모든 변수에 대한 편미분과 미소 증분의 곱들의 합

미분(도함수) derivative

- 함수 f : (a, b) -> R이 주어질때 아래의 극한값

상미분 ordinary derivative

- 일변수 함수의 미분

고차 미분 high order derivative

- 함수 f(x)가 주어질때 여러번 미분한 것

평균값 정리 mean value theorem

- 구간 [a, b]에서 미분 가능한 함수 f(x)가 존재할때, 그 사이에서의 기울기 값들도 존재

테일러 급수 talyor series

- 함수 f(x)가 주어질 때, x*에서 미분 가능한 경우 무한 다항식의 합으로 정리할수 있음

 * 거듭 제곱 급수를 정리하여 구할 수 있음.

용어 정리

- 최소자 minmizer : f(x)를  최소로 하는 x

- 최소값 minimum : 최소인 f(x)

- 임계지점 critical point : f'(x) = 0인 지점 -> 임계점에서 함수 f(x)는 최소값 or 최대값이 됨

- 전역 최소자 global minimizer : 모든 범위에서의 최소값

- 지역 최소자 local minimizer : 일부 구간에서의 최솟값

2020-07-17

• 지난 시간에는 최적화를 본격적으로 다루기에 앞서 선형 대수를 복습하면서 기존에 알고 있던 내용들은 다시 확인하고, 확실하게 정리되지 않았던 벡터 공간과 고유치,고유벡터, 분해, 그리고 그림 슈미트 직교화 등에 대해서 살펴보면서 조금씩 조금씩 부족하게 알고 있던 내용들을 채워나갈수 있는 기회였습니다. 이후 공간에서 회전을 다루는 군과 행렬에 있어서의 분해 방법들을 보면서 선형대수를 마무리하고, 실제 최적화 방법들을 다루기 전에 필요한 함수들에 대한 다양한 개념들을 살펴보면서 학습을 마무리하였습니다. 단 이번에는 블로그 상에 올리지는 못한채로 정리하였습니다.
• 우선 지난번에 살펴본 군은 어느 이항 연산자와 관련된 연산들을 만족하는 집합을 군이라고 불렀는데, 이러한 군중에서 공간상에서 물체의 회전에 대한 군들을 살펴보았습니다. 이때 회전 군은 3차원 행렬을 하나의 원소로 하고 있는데, 이러한 회전 군으로 대표적으로 오일러 각이 있었습니다. 오일러 각은 각 축에 대한 회전량 만큼을 행렬로 나타내고 있어, 즉 X축에 대한 회전행렬, Y축에 대한 회전행렬, Z축에 대한 회전 행렬로 구성이 되어있으며, 가장 이해하기 쉬운 회전 표현이지만 자유도가 사라지게 되는 짐벌락 현상의 문제로 오일러각을 대체하는 쿼터니언이라는 방식이 있습니다. 쿼터니언은 합이 1인 4개의 숫자로 오일러 각에 비해서 회전 형태를 이해하기는 힘들수는 있으나 짐벌락 현상이 발생하지 않으며, 컴퓨터 연산을 고속으로 할수 있는 장점을 가지고 있었습니다.
• 그 다음으로 특이값 분해와 촐래스키 분해에 대해서 간단히 살펴보았습니다. 특히, 특이값 분해는 이전에 영상 처리를 공부하면서 잠시 살펴본 적이있었는데, 당시 이런 선형대수에 대한 배경지식없이 단편적인 특이값 분해를 보았을때 도저히 이해할수가 없었습니다. 하지만 앞선 행렬로부터 대각 성분을 분해하여 이차 형태를 만드는 과정을 살펴보고 난 이후여서인지 조금 수월할수 있었습니다. 특이값 분해에서는 주어진 행렬을 두 직교 행렬과 특이값들로 이루어진 하나의 대각 행렬로 분해하여 이차 형태를 만드는 방법임을 확인하고, 특이 값 분해로 추정을 하기 전에 선형 시스템을 잠시 살펴보았는데, 선형 시스템은 변수의 개수와 방정식의 수에 따라서 소거법으로 해를 구할수 있으나, 정확한 해를 구하지 못하는 경우도 존재합니다. 그 때 오차가 최소가 되도록 하는 근사 해를 최소 제곱법을 이용하여 구하여야 하는데 이때 특이값 분해를 이용해서 근사해를 구하는 과정을 살펴보았습니다. 이후 행렬이 양 확정행렬일때 사용하는 촐레스키 분해에 대해간단히 살펴보면서 선형대수 복습을 마무리 하였습니다.
• 다음으로 최적화를 다루기에 앞서 다양한 함수들을 살펴보았는데, 우선 가장 간단한 경우인 일변수 함수에 대해서 알아보았습니다. 이 개념은 공업 수학에서 이미 살펴보았기 때문에, 일변수 함수의 미분(도함수)인 상미분 정의를 살펴보고 빠르게 지나갔으며, 중간값 정리, 거듭 제곱 급수에서 계수를 정리하여 구한 테일러 급수를 알아보았습니다.
• 이후에는 이 테일러 급수에서 1차 미분을 0으로 하여 최대값을 찾는 2차 미분 테스트를 알아보고, 최적화에서 사용되는 함수에서의 최소 지점인 최솟값과 최솟값을 찾는 변수 x의 값인 최소자 그리고, 전역과 지역에 따라 전역 최소자와 지역 최소자, 그리고 기울기가 0인 임계 점등의 개념들을 살펴보았습니다.
• 마지막으로 다변수 함수 개념에 대해서 보았는데, 이 또한 공업 수학에서 살펴본 덕분에 간단하게 알아보았습니다. 우선 다변수 함수는 n 벡터공간에서 m 벡터공간으로 정의하는 함수로서 대표적으로 이변수 함수가 있는데, 여기서 2변수 함수를 이용한 행렬 형태를 이차 형식이라고도 합니다. 여기서 이차 형식은 선형대수를 다루면서 종종 볼 수 있었고, 이 외에도 삼변수, n변수 함수로 분류하기도 합니다.이후 내용은 이전과 마찬가지로 다변수 함수에서의 테일러급수를 살펴보면서 마무리하였습니다.