728x90
군 이론 group theory
- 컴퓨터 비전과 컴퓨터 그래픽스에서 자주 등장하며, 다음과 같은 군들이 있다.

군 이란?
- 집합 G가 이항 연산자 *에 대해 다음 조건들을 만족하는 경우의 집합.
=> (G, *)은 군 group이 됨.
1. 결합 법칙
2. 항등원, 역원의 존재
3. 아래와 같이 교환법칙이 성립하는 경우 -> (G, *)는 가환 군 commutative group

군의 종류
1. 가환군 commutative group
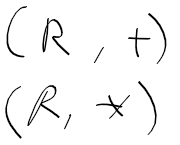
2. 비가환군
- 공간상 물체의 평행 이동을 의미하는 군

- 행렬식이 0이 아닌 행렬의 집합 : general linear group

- 위 집합의 부분군이며, 회전을 나타내는 집합
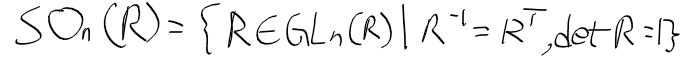
3차원 벡터 공간에서의 직교 행렬
- 직교행렬 orthogonal matrix : 다음의 경우를 만족하는 행렬

- 직교행렬의 모임은 아래와 같다.

직교 행렬의 성질
1. 정규 직교 행렬의 거리(노름)은 불변
- 정규 직교 행렬 U와 벡터 x이 주어질때 노름을 구하면 다음과 같다.

2. 직교행렬 U의 열 벡터 U1, U2, U3는 3차원 벡터 공간의 정규 직교 기저 orthnormal basis
- O_3(R)은 직교군 orthogonal group
- U가 O_3(R)의 원소라면, 정규직교 기저로 이루어진 직교행렬들은 다음과 같은것들이 존재함.
300x250
'수학 > 선형대수, 최적화' 카테고리의 다른 글
| 최적화 - 2. 1 변수 함수 (0) | 2020.07.20 |
|---|---|
| 선형대수 - 12. 회전 (0) | 2020.07.18 |
| 선형대수 - 10. 외적과 마할라노비스 거리 (0) | 2020.07.16 |
| 선형대수 - 9. 거리와 내적 (0) | 2020.07.16 |
| 선형대수 - 8. 그람슈미트 직교화 과정 (0) | 2020.07.16 |