집밖은 위험해

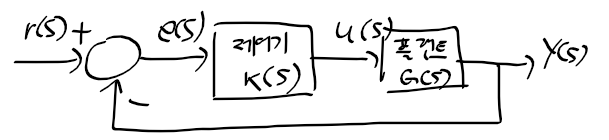
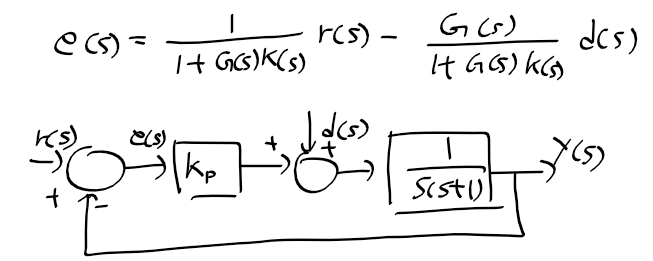
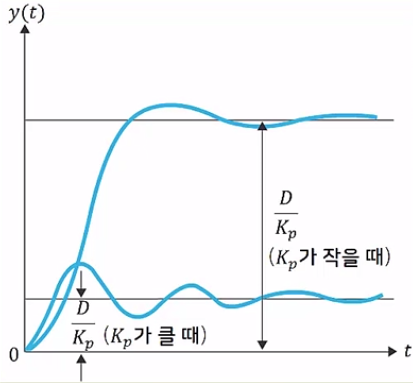
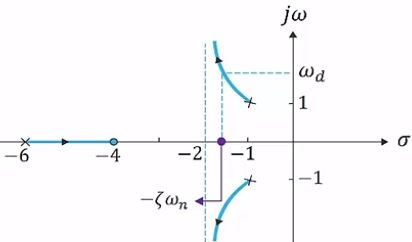
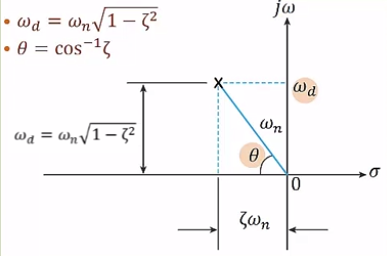
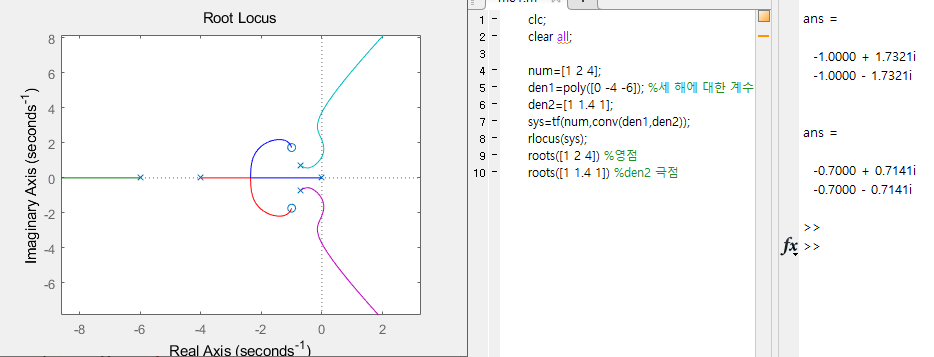
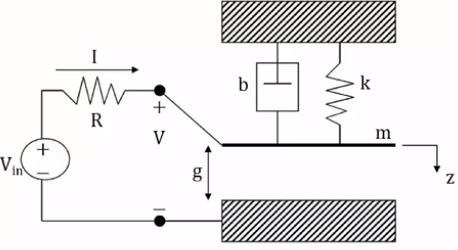
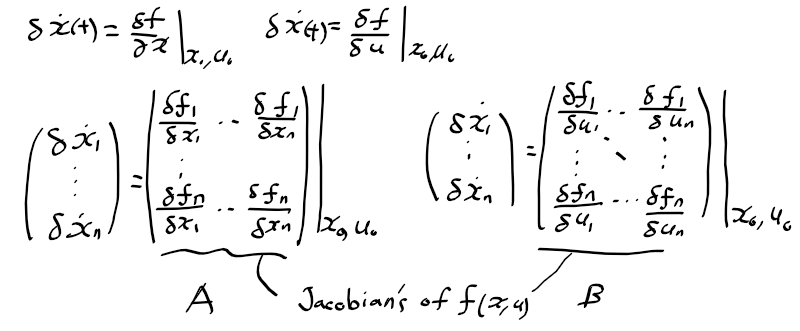
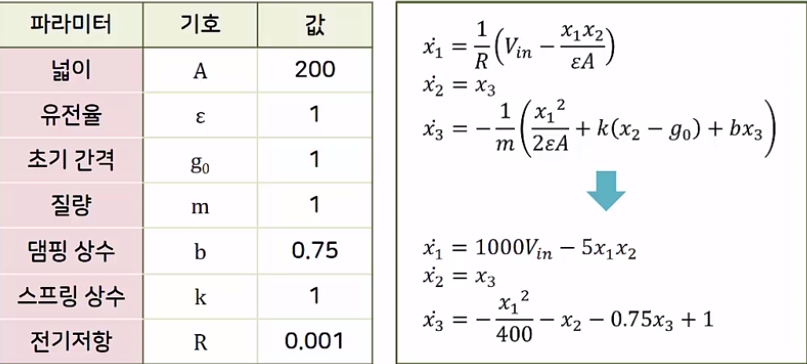
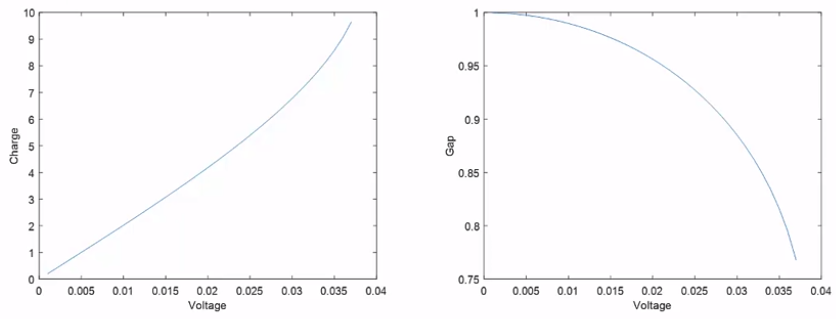
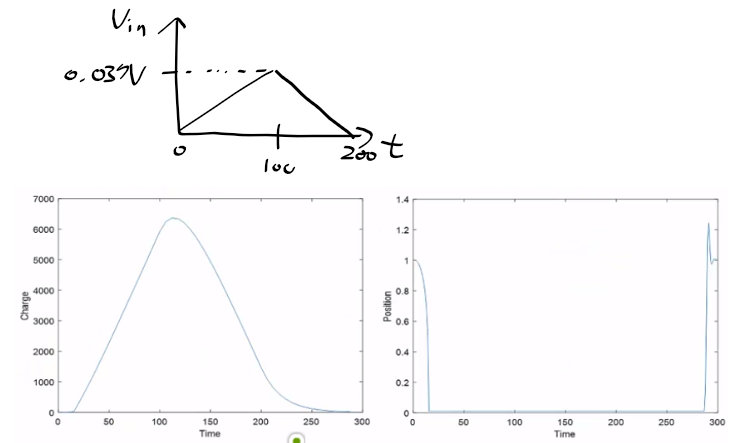
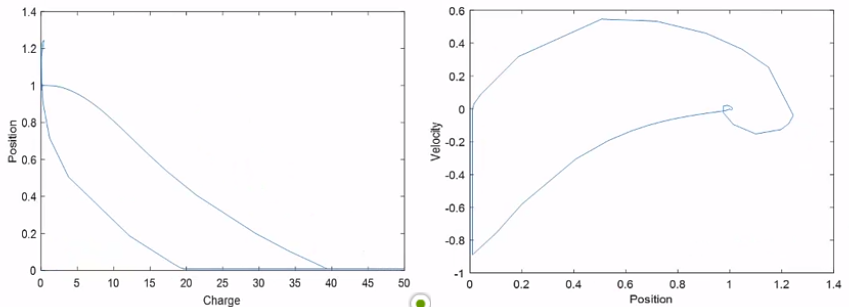
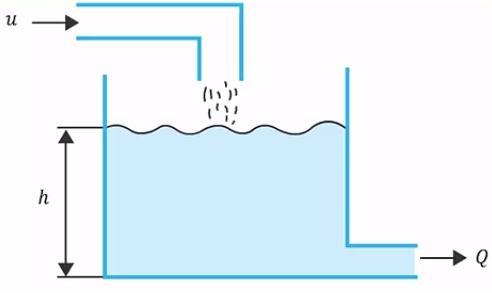
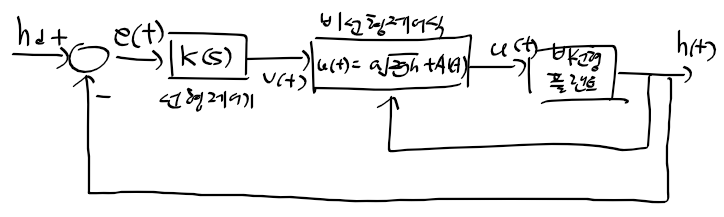
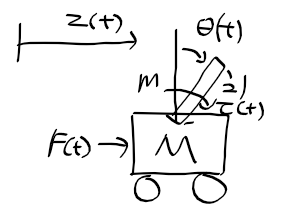
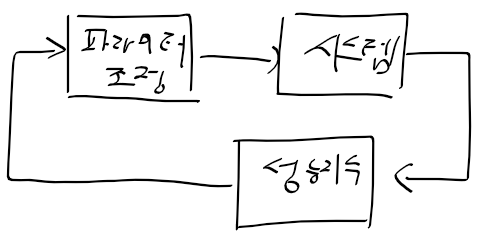
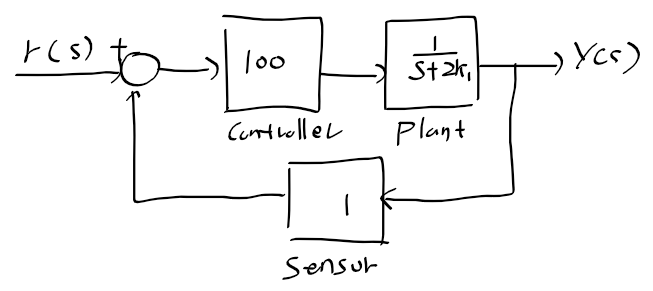
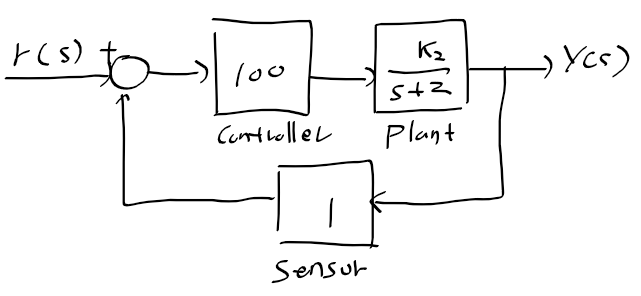
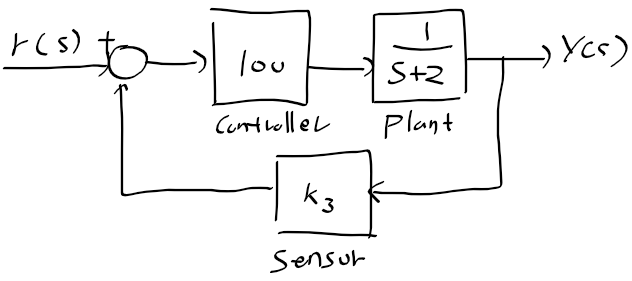
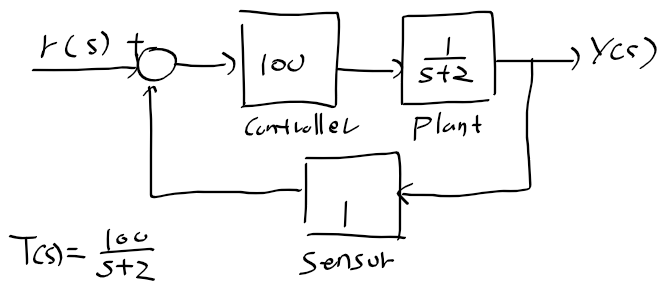
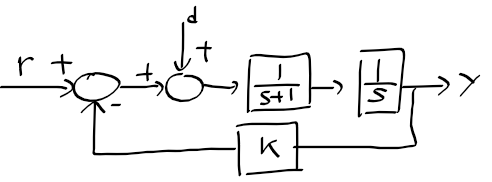
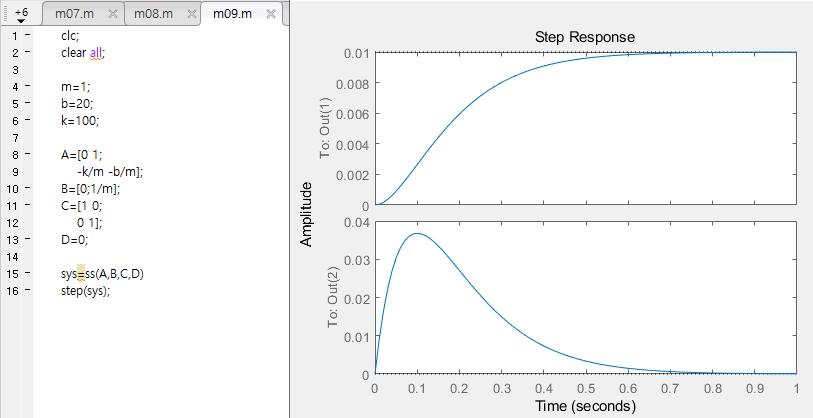
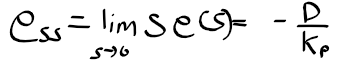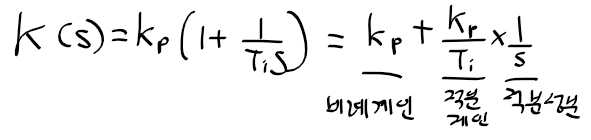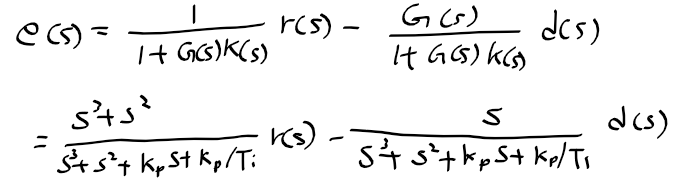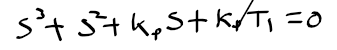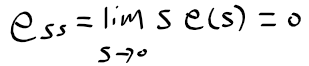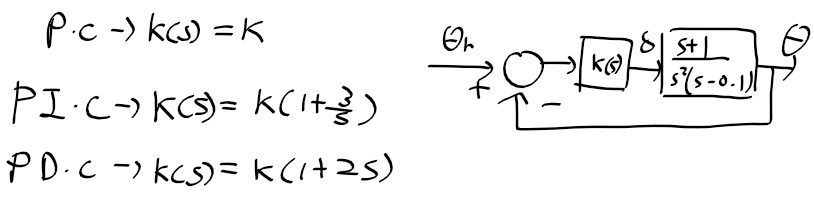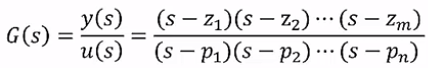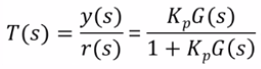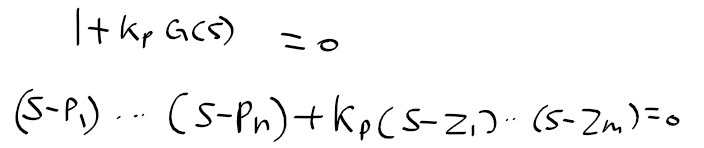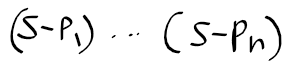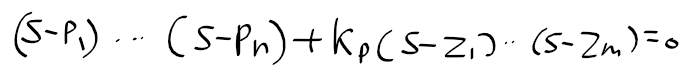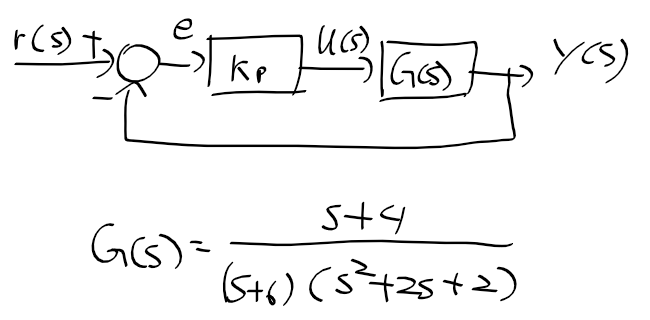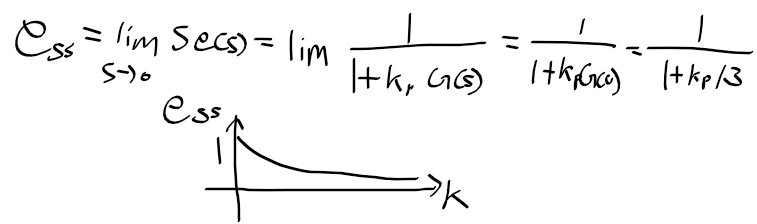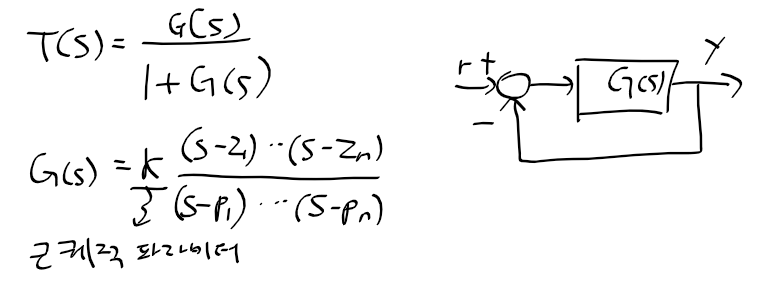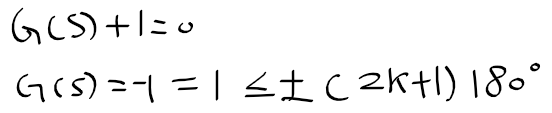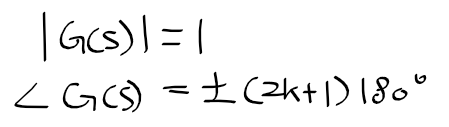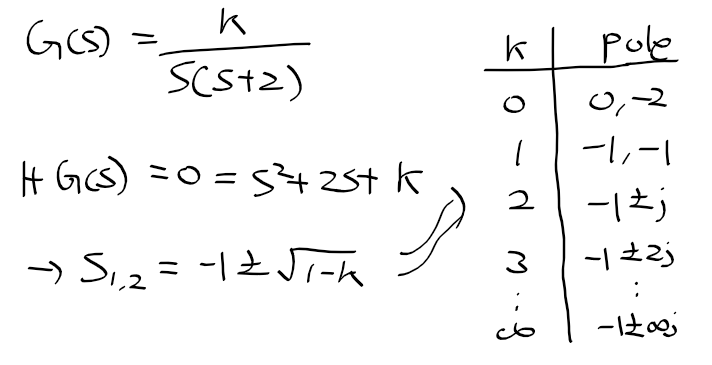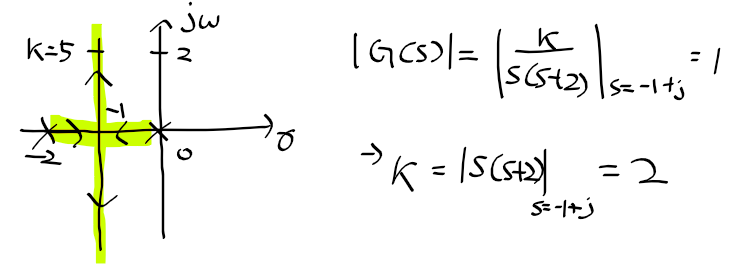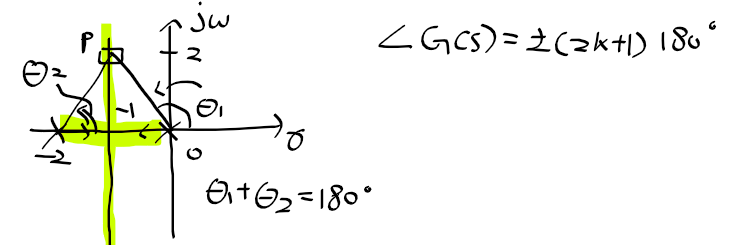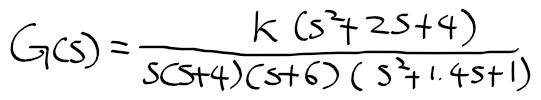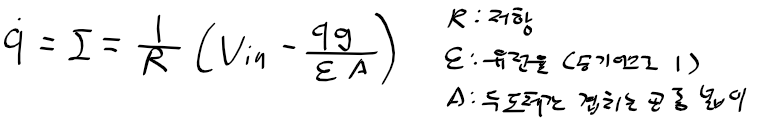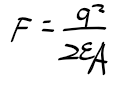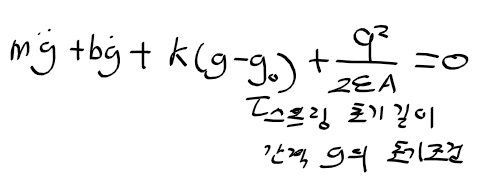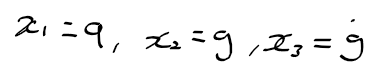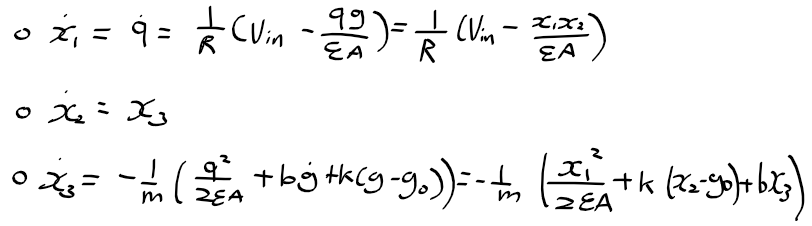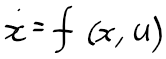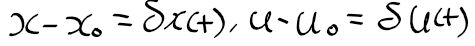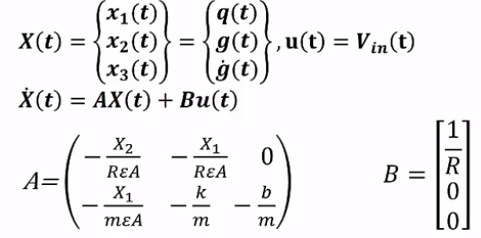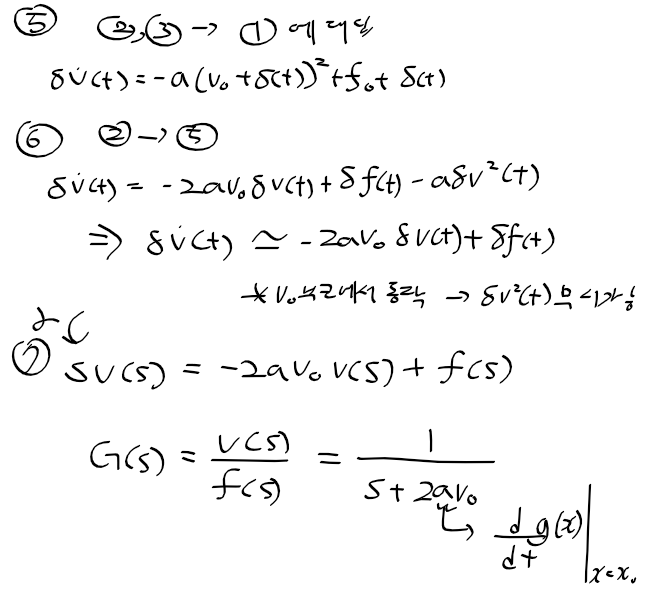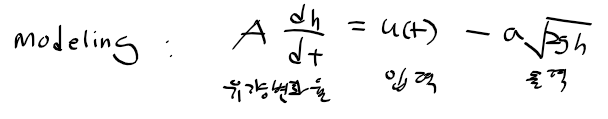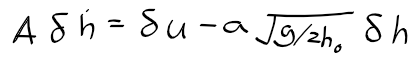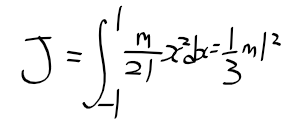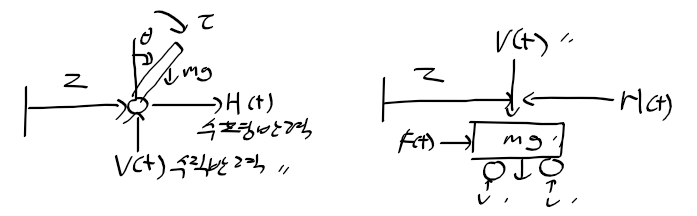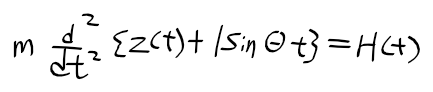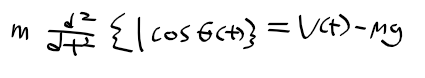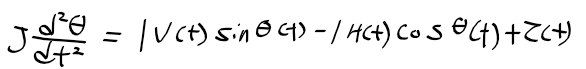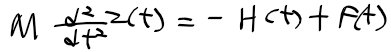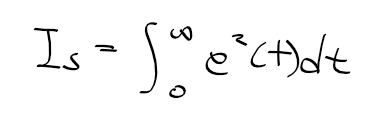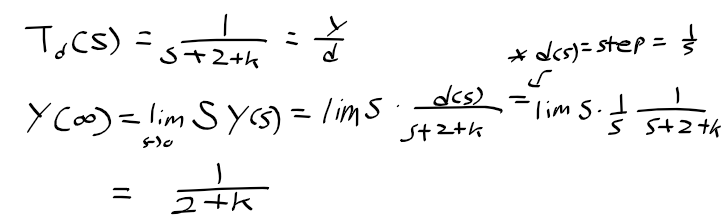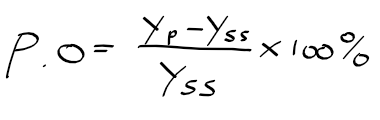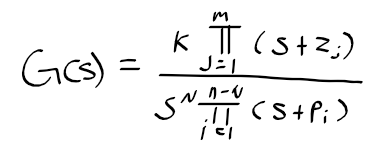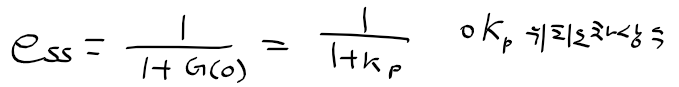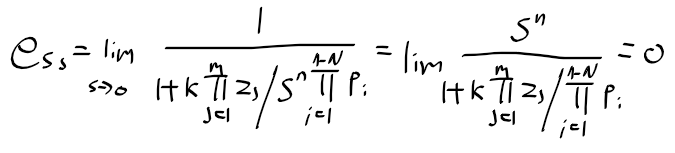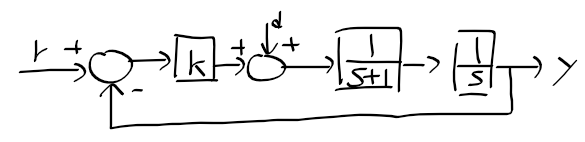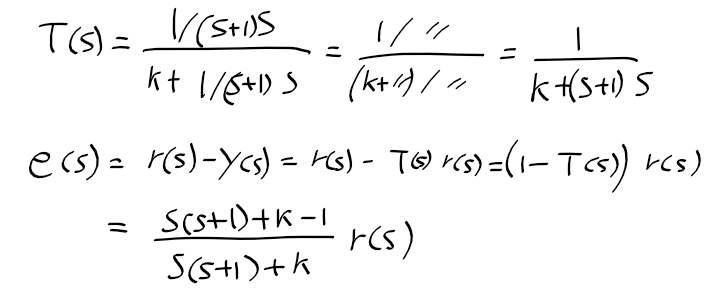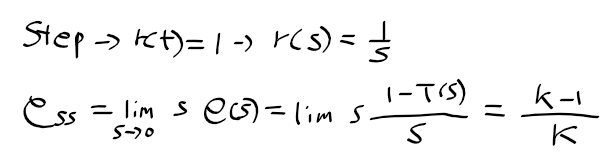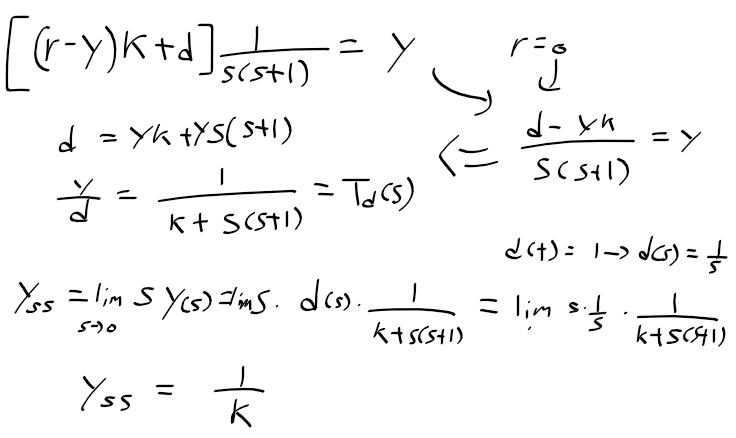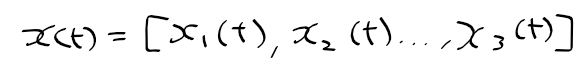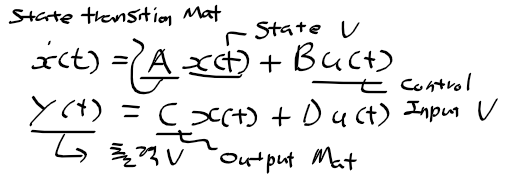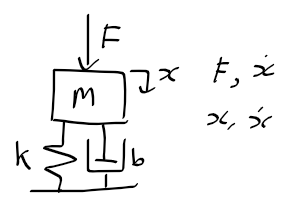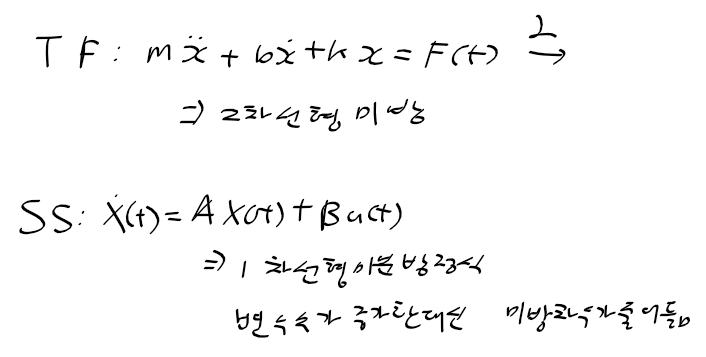근궤적을 이용한 적절한 이득 결정

- 근궤적으로 이득 구하기 힘든 경우도 있음

-> 앞섬 보상기 사용

앞섬 보상기

- 원하는 근의 위치를 정함

- 근궤적이 근을 지나도록 설계

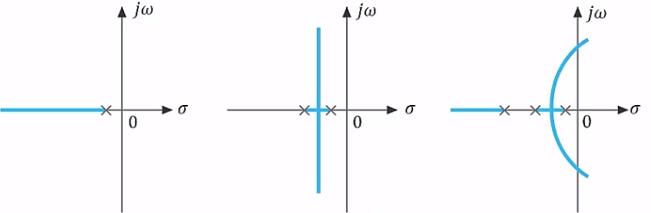
극점 첨가 효과

- 근궤적을 s평면의 오른쪽으로 끌어오는 효과가 있어 안정성이 감소

- 시스템 감쇠비가 작아져 오버슈트가 증가하고 정착시간이 길어짐

- 적분 제어 요소를 첨가하는 효과와 비슷하게 정상상태 응답을 개선할 수 있음(정상상태 오차를 줄일수 있다)

영점 첨과 효과

- 근궤적을 왼쪽으로 끌어오는 효과

- 시스템의 감쇠비가 커져 오버슈트가 감소하고 정착시간이 짧아짐

 * 허수축의 가깝던 근궤적이 멀어짐 -> 빨리 수렴 -> 정착시간이 줄어듬

- 미분제어 요소 첨가하는 효과와 비슷하여 과도 상태에서 큰 제어 입력이 필요

- 영점의 위치가 허수축에 가까울수록 영점 효과가 큼

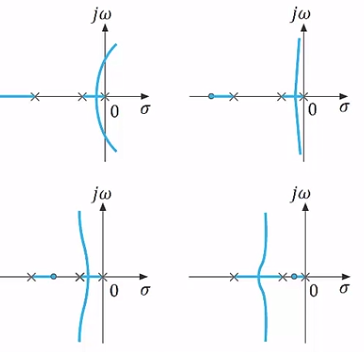
극점 첨가의 효과

- 과도 응답을 고려 시 영점 첨가가 좋으나 정상상태 응답 개선을 위해 극점 첨가가 필요

극점과 영점의 혼합

- 실제 구현가능한 제어기에서 극점의 개수가 영점 갯수보다 많거나 같으므로 혼합이 바람직

앞섬 보상기 lead compensator

- 시스템 응답 속도를 개선하고 정상상태 정확도를 개선하고자 할때 사용

- 위상 앞섬(phase lead) 발성

 -> 모든 주파수에 대해 K(jw) 위상이 항상 +

- 앞섬 제어기 영점은 항상 극점의 오른쪽에 있음

- alpha 값이 작을수록 극점은 왼쪽 멀리 위치

- 하드웨어적인 문제로 alpha의 실제 최소값은 0.07
=> 영점과 극점의 위치를 어디에 둘것인가 고려하여 정해야한다.

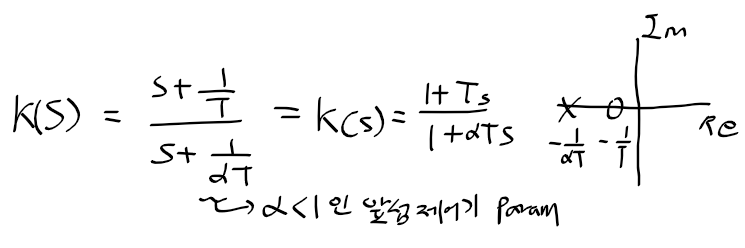
앞섬 제어기 효과

1) 시스템 안정화 (+과도응답 특성)

- 제어기 영점은 근궤적을 s평면 상에서 왼쪽으로 움직이게 함

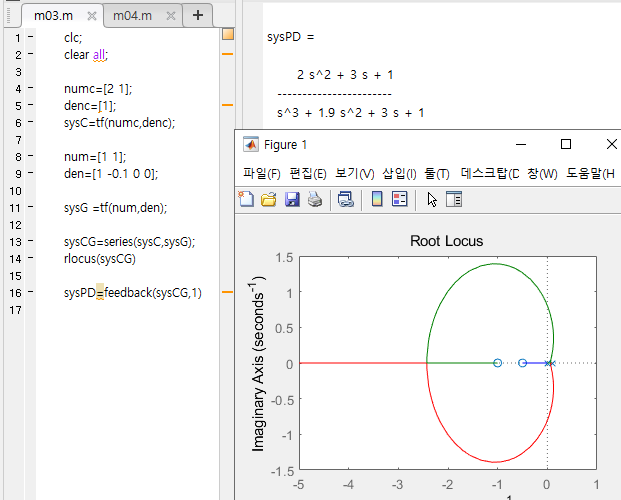
예제 : G(s) = K/s(s+1) 인 DC 모터에 PD 또는 앞섬 제어기 적용

 - PD 제어기 전달함수

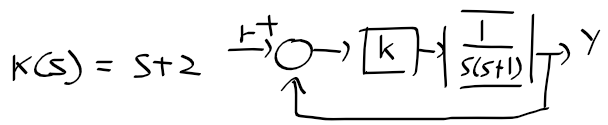
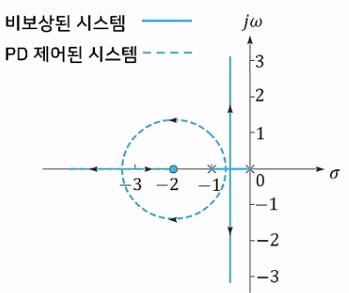
PD 제어기 문제점

- 순수 미분기는 실제 물리 시스템에서 존재 할 수없고, 센서에 의한 고주파 잡음을 증폭시킴

=> s=-alpha에 극점이 첨가된 앞섬제어기를 사용하는 것이 바람직함

앞섬 제어기 전달함수

- PD 제어기에 s=-alpha인 극점을 추가한 앞섬제어기의 전달함수

앞섬 제어의 효과

- 양쪽 근궤적에서 이득 K가 작은경우 PD 제어와 효과 유사(허수축에 가까우므로)

- K가 커지면서 앞섬제어 효과가 두드러짐

극점과 영점의 결정

- 영점은 정착시간을 고려하여 결정(미분 유사 효과)

- 극점은 영점의 3~20배 위치에 놓아 정상상태 오차를 줄임(적분 유사 효과)

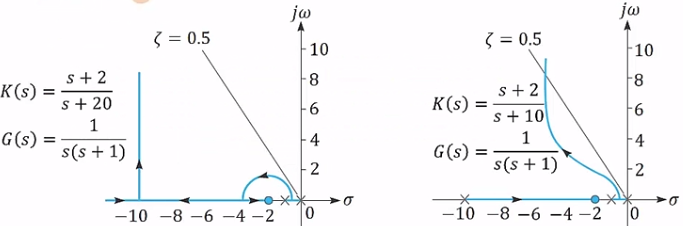
과도응답 특성이 정해진 경우

- 앞섬제어기

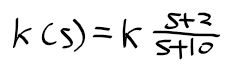
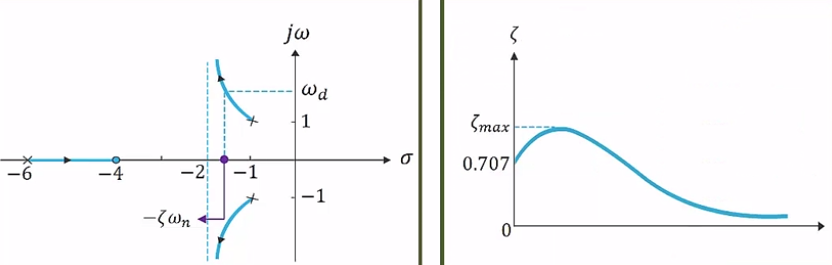
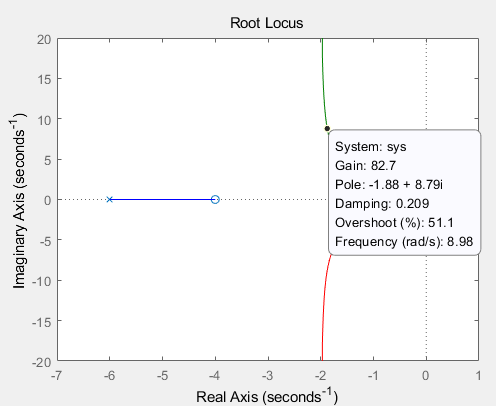
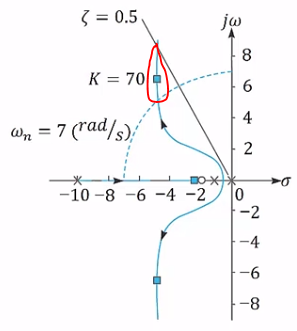
- 근궤적이 아래의 그림과 같을 때

 감쇠비 > 0.5, 고유주파수 > 7(rad/s)를 만족하는 이득을 원한다면

1) 감쇠비 > 0.5 -> zeta=0.5 선의 좌측

2) 고유주파수 > 7(rad/s) -> wn=7(rad/s) 점 선의 좌측

=> K=70, 조건을 만족하는 K는 하나가 아님

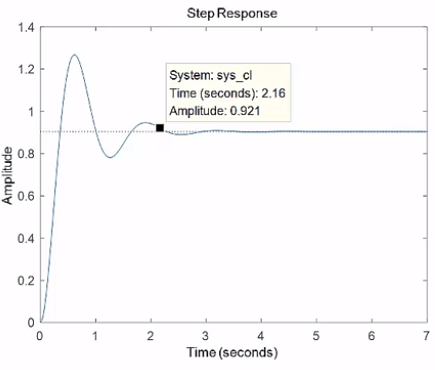
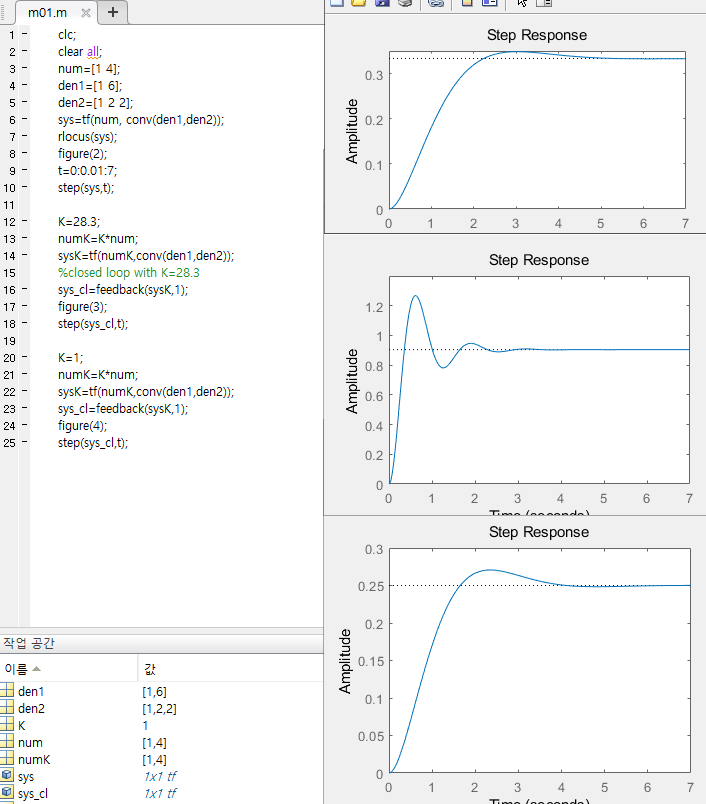
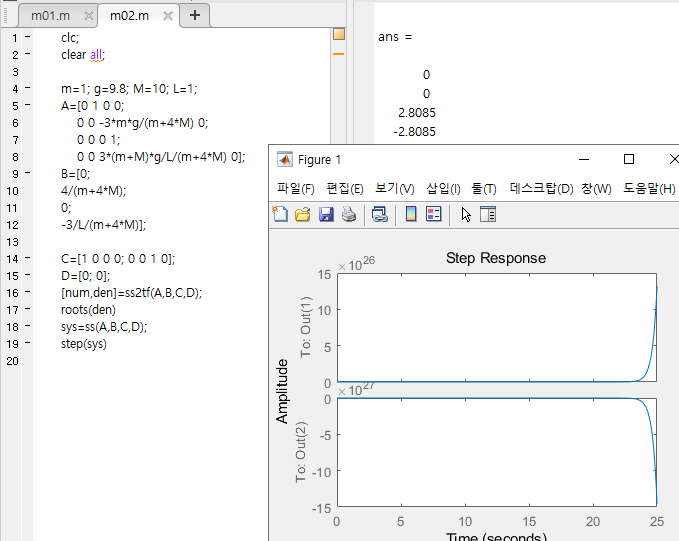
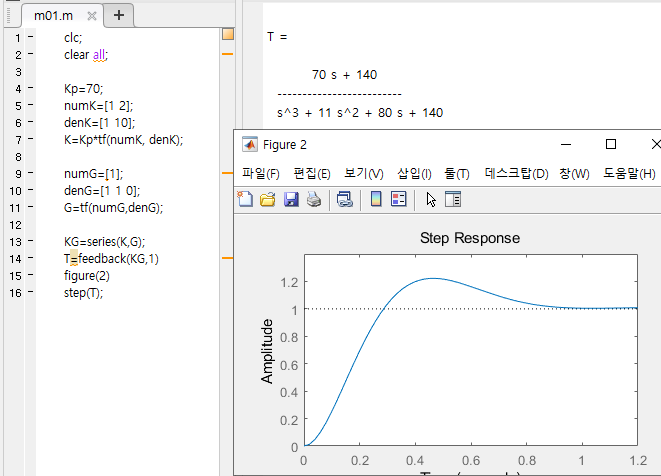
앞섬 제어기가 포함된 폐루프의 스텝응답

- 아래의 앞섬 제어기를 포함시킨 폐루프 시스템의 스텝 응답

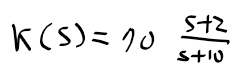
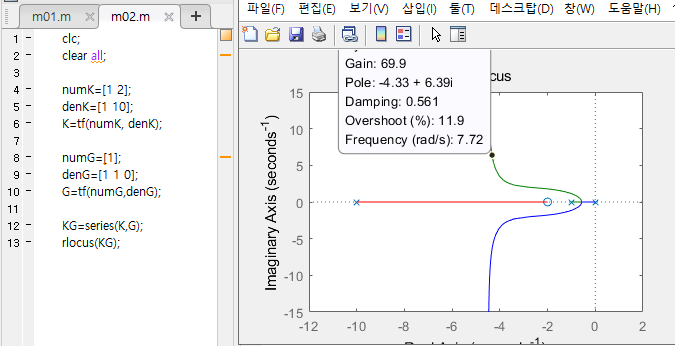
앞섬제어기가 포함된 폐루프의 근궤적선

- 게인이 70일때 damping > 0.5, wn > 7 조건 만족 + 오버슈트 12%

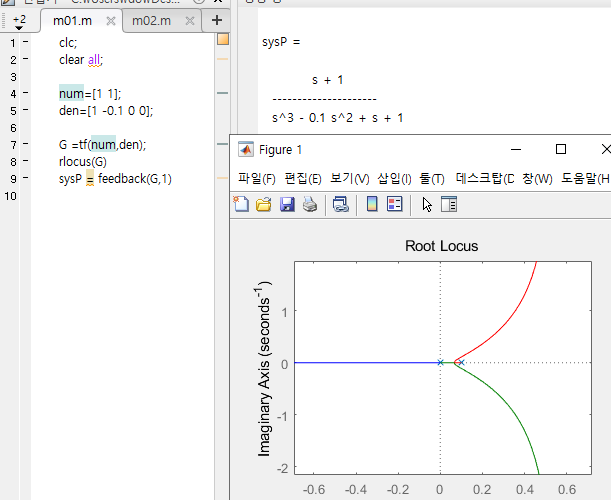
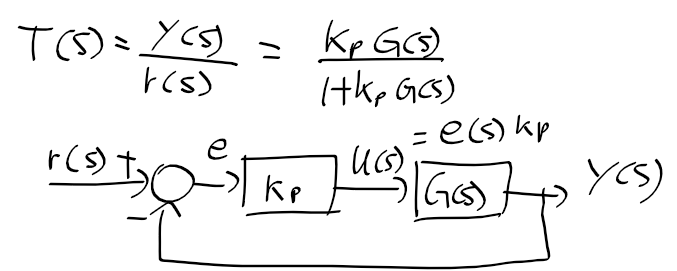
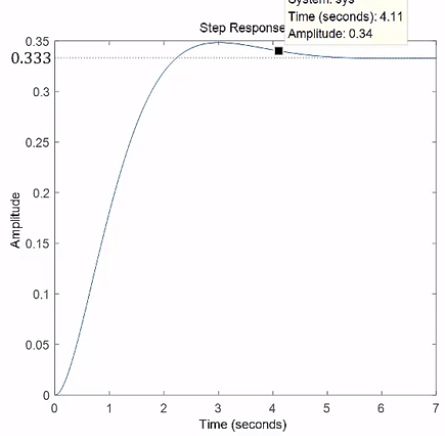
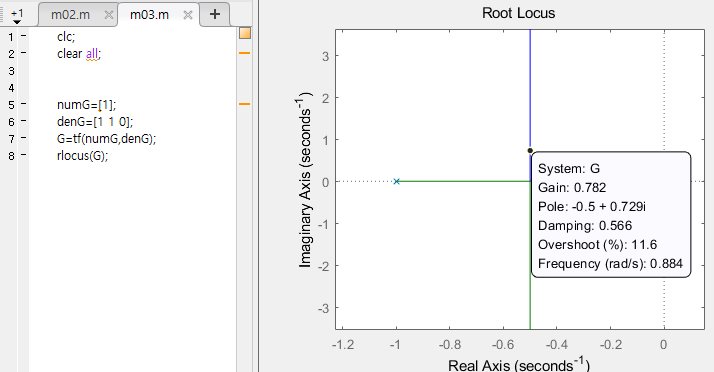
 비례 제어기만 있는 폐루프 시스템의 근궤적선

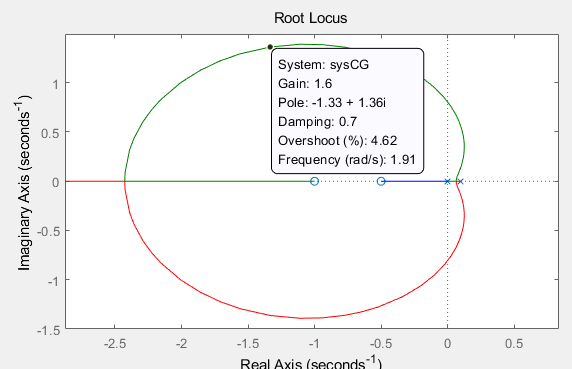
* 게인이 0.782 인경우

 댐핑비 : 0.566

 고유주파수 : 0.884

- 앞섬제어기에 비해 허수축에 가까이 위치함

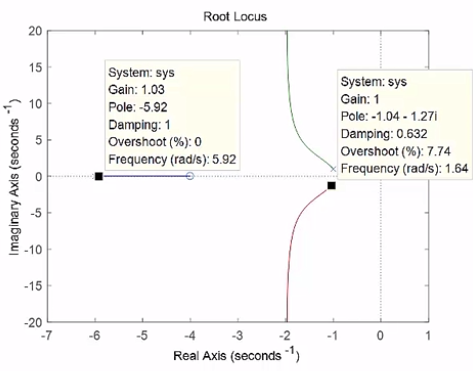
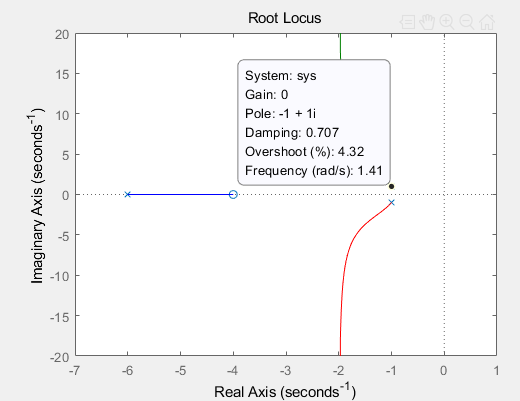
원하는 극점이 있는 경우

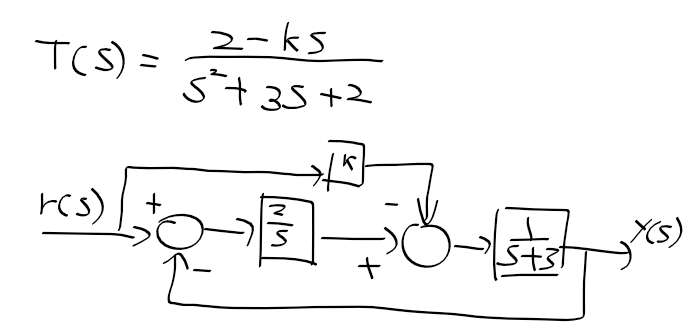
- 감쇠비 = 0.5, 고유주파수 = 2(rad/s)가 요구되는 경우 => 앞섬 제어기로 옮기자

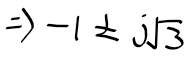
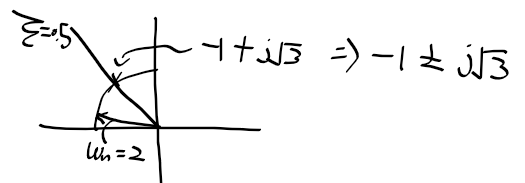
원하는 근에서 플랜트 개루프함수 G(s)의 위상 = -210도

1) 제어기 K(s)에 위상 30도를 주아 위상조건식 -180도 만족

2) 제어기 영점이 -2로 정해지면 극점을 -4에 위치시켜 30도 만족

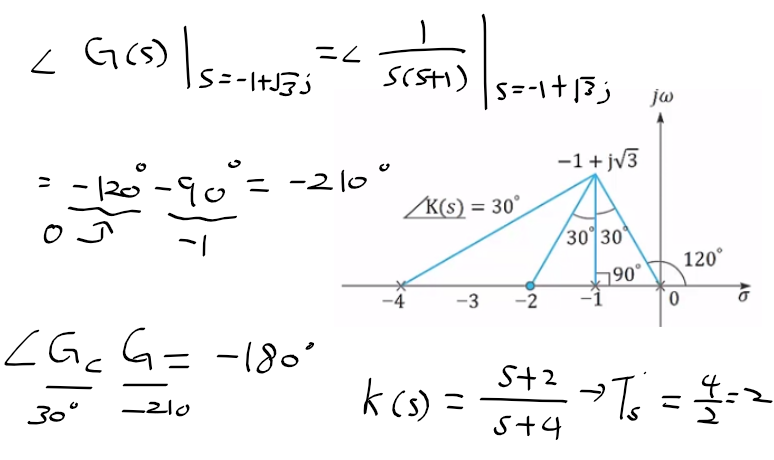
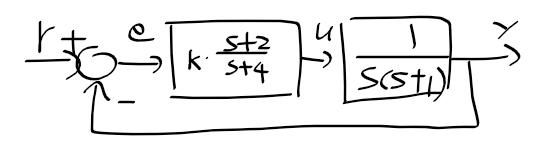
앞섬제어기가 추가된 블록선도

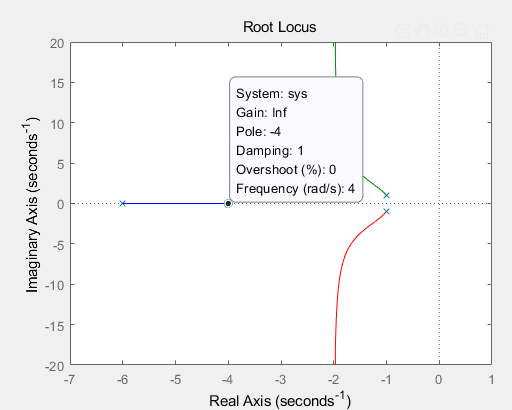
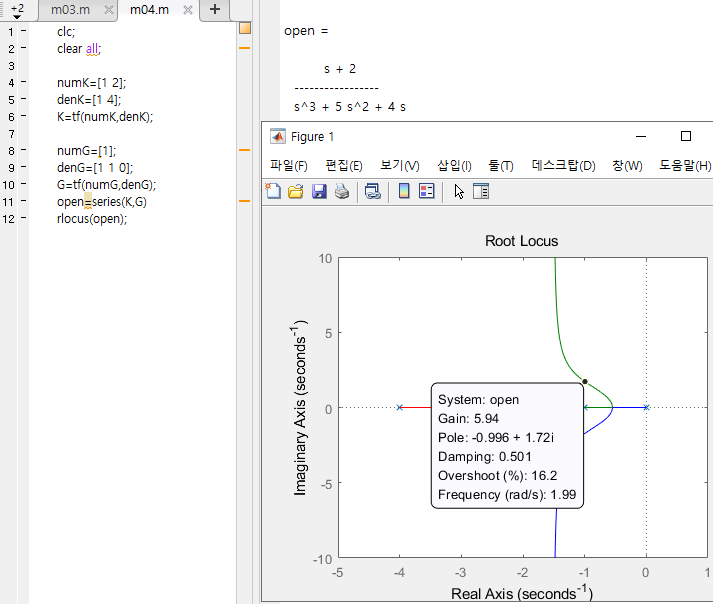
근궤적선으로 조건을 만족하는 게인 찾기

- 게인이 5.94 일때

 -> 감쇠비 : 0.5, 고유주파수 =2(rad/s) 만족

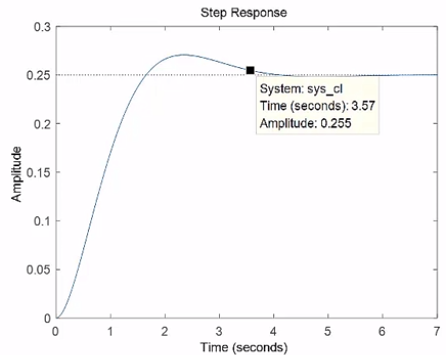
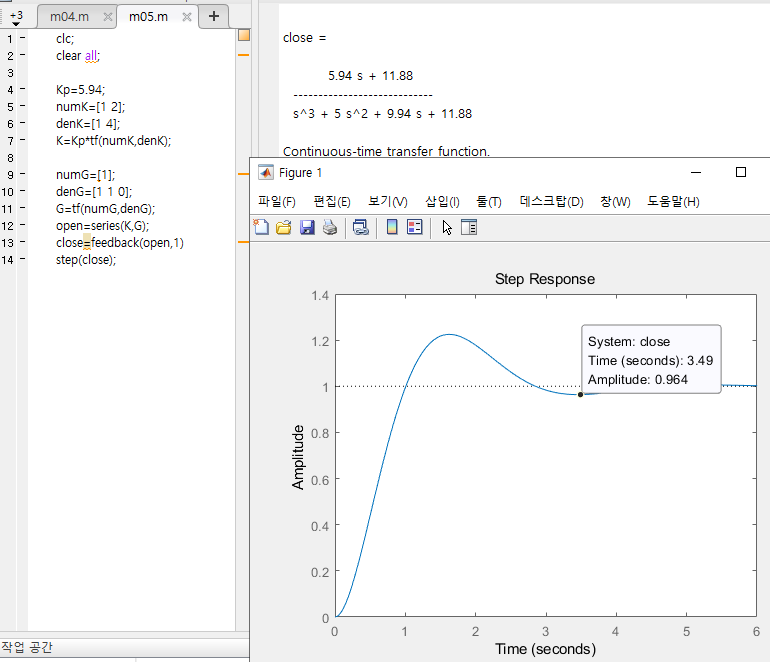
해당 조건에 대한 스텝 응답

비례적분미분제어 proportinal integral differential control

- 일반적인 형태의 피드백 시스템

- 부족한 정상상태응답 특성

- 시스템 안정도 개선에 필요한 적분/미분 요소 => 플랜트 입력

- 각 제어기의 적절한 이득을 결정하는것이 핵심

제어 시스템 설계 절차

- 제어기 전달함수의 형태 선정

 -> 비례제어, 비례미분제어, 비례적분제어를 할지 셋다 할지 등

- 설계 파라미터들을 해석적인 방법으로 적절히 선정

- 설계된 제어 시스템의 안정도 및 성능 검토

- 성능이 불만족한 경우 -> 요구된 성능을 얻도록 반복 수행

제어기 설계만으로 요구 성능 불충족시

- 플랜트 구조나 재료 변경 또는 수동적 감쇠 효과 보강 등 플랜트 동적 특성 자체 변경

- 센서 및 구동기를 추가 또는 재배치

일반적인 제어 시스템

- 제어기 출력이 플랜트 입력이 되는 제어시스템

- 제어기 형태에 따른 분류

-> 비례, 비례적분, 비례미분, 비례적분미분 제어기

적분 제어 요소

- 적분 요소를 포함한 플랜트에 대한 비례 제어 시스템 오차

* 적분요소 포함 : 극점 중 하나가 0 = 전달함수에 1/s를 곱함. 

적분 요소를 포함하는 플랜트의 스텝 입력에 대한 비례 제어의 정상상태 오차

-> 외란에 의해 0이 되지 않음

비례 제어이득 K_p를 증가시키는 경우

- 정상상태 위치 오차를 줄일수 있음

- 큰 제어량이 요구되며 진동 출력이 심함

외란이 큰 경우

- 비례 제어만으로 부족

PI(비례적분) 제어기의 전달함수와 정상상태 오차

- 비례적분 제어기의 전달함수

- 비례적분 제어기의 오차

- 플랜트에 대한 PI 제어시스템의 특성방정식

 -> PI 제어 게인 Kp/Ti에 따라 시스템이 불안정 해질 수 있음

비례적분 제어시스템의 정상상태 오차

- 스탭 입력에 대한 정상상태 오차

* 적분 제어 요소

- 일정 입력에 대해 정상상태 오차를 발생하지 않도록 함

- 시스템 안정도 저해

미분 제어 요소

- 오차 신호 변화에 따라 동작 -> 미분 제어 요소만 사용할 수 없음

* e_dot(오차 변화량) x K_d(미분 게인)

- 초기에 큰 제어량이 요구됨

- 시스템 안정도 개선

- 감쇠 효과 -> 시스템 이득을 증가시켜 정상상태 오차를 줄임

이중적분 요소를 포함한 플랜트에 대한 비례제어 시스템 응답(1/s^2)

- 폐루프 시스템 전달함수 (T(s))로부터 특성 방정식이 두 허근을 가짐

- 무한 진동을 하므로 안정화 필요

비례 미분 PD 제어기

- Kp, Td 값에 따라 오버슈팅이 커질 수 있음

비례적분미분 PID 제어기

- 산업현장에서 가장 많이 사용되는 제어기

- 비례 적문 미분 제어기의 전달함수

kp : 비례 게인, ki : 적분 게인, kd : 미분 게인

Ti : 적분 시간. Td : 미분 시간

배의 자동 조차 시스템 설계

- 조타 각 : delta, 배가 향하는 각도 : theta

 플랜트 전달함수

- 아래의 전달함수 극점 하나가 양의 실수 -> 안정화 필요

배의 자동조타를 위한 제어 시스템 설계

- 제어기 K(s)의 형태

희망 설계 사양

- 단위 스텝 기준입력, 단위 램프기준입력에 대해 정상상태오차 = 0

- 폐루프 시스템의 감쇠비 = 0.707

비례 제어

-불안정

비례 적분 제어

- 불안정

비례미분제어기

- 안정

단위 스텝 입력/단위 램프입력에 대한 정상상태 오차

- 단위 스텝/램프 입력에 대한 정상상태 오차가 0이 됨

-> 감쇠비만 맞추면 됨

요구되는 감쇠비

- zeta=0.707인 게인을 찾으면 됨

-> 제어기 게인 K=1.6 정도

비례제어 proportional control

- 오차 x 적절한 크기 이득 = 플랜트 입력

- 근궤적을 이용해 이득 결정

비례제어이득을 갖는 폐루프 시스템

- 에러에 상수 k_p를 곱하여 G(s)의 인풋으로 사용되는 시스템

개루프 시스템

- 입력에 대한 시스템 출력 응답 G(s)의 특성방정식 근들중 근의 실수부가 허수축에 가까운 근의 위치에 의해 결정됨

폐루프 시스템

- 입력에 대한 시스템 출력 응답은 T(s)의 특성방정식 근중 실수부가 허수축에 가까운 근의 위치에 의해 결정됨

- kp에 의해 특성방정식 근의 위치가 변할 수 있음.

G(s) 특성방정식의 근

- 개루프 전달함수 극점들의 변경이 필요할 때

 -> 플랜트 파라미터 변경이 필요

T(s)의 특성방정식 근

- k_p를 이용해 제한적이지만 근의 위치를 변경가능

 -> 플랜트 파라미터 변경이 불필요함

비례 제어 시스템 해석

비례 제어

- 기준값 r(s)와 출력의 오차인 e(s)에 이득 k_p을 곱한 값을 제어 대상인 플랜트의 입력 u(s)로 하는 제어기법

- 오차에 비례한 값이 플랜트의 입력이 되므로 비례제어라 함

비례제어와 근궤적과의 관계

- 비례제어 효과 : 근궤적으로부터 예측 가능함

- 비례제어 이득 결정 방법 ; 근궤적으로부터 시스템이 원하는 정상상태응답과 과도응답 특성을 나타내는 이득을 정하게됨

비례시스템 예제

- 영점 : -4

- 극점 : 3개 -> -6, 복소수 극점 2개

theta 값으로 감쇄비를 알수 있음

근의 실수부 크기 = zeta * 고유 진동수 w_n

감쇄비 허수축 크기 = 감쇄 고유주파수 w_d

1.  허수축에 가까운 두 극점 위주로 보아야 함

2. 감쇄비의 변화를 보면 어느 시점에서 최대(zeta_max)가 되고 0으로 수렴

폐루프 시스템의 정상상태 오차

개루프 시스템과 비례제어이득이 k_p=28.3인 폐루프 시스템의 스텝응답

1) 개루프 시스템의 스텝 응답

- 수렴하는 값이 0.333 이므로 e_ss=0.667

- P.O = 4.8%

- T_s = 4.11초

2) 폐루프 시스템의 스텝응답 K_p=28.3

- 수렴하는 값은 0.904로 스텝입력 1과 e_ss = 0.096의 정상상태 오차를 보임

- PO는 40.5%

- T_s=2.16초 나타남

- 과소 감쇄 형태

폐루프 시스템의 스텝응답 (k_p=1)

- 수렴하는 값은 0.25로 스텝입려 1과 e_ss=0.75 정상상태 오차를 보임

- PO는 8.0%

- T_s=3.57초

근궤적 1

- 극점 -6에서 시작할때 게인이 무한대로 증가할때 근은 영점인 -4에 가까워짐

근궤적 2. 게인이 0인 경우

- 댐핑비 : 0.707

- 퍼센트 오버슈트: 4.32

- 자연주파수 : 1.41

근궤적 2

- 근 -1+j에서 시작하여 게인 값이 증가할때 근의 실수부는 -2에 가까워지고, 허수부는 점점 증가

근 궤적법

- 오차 x 적절한 이득 = 플랜트 입력

- 근궤적법으로 적절한 이득을 쉽게 구할 수 있음

근궤적법 root locust method

- 1948 W.R Evans 개발

- s평면상 개루프 전달함수의 극점, 영점 배치와 시스템 파라미터 값 변화에 따른 폐루프 극점의 위치를 알아내는 그래픽적인 방법

근궤적법 장점

- 시스템 파라미터 값 변화에 따른 폐루프 극점 위치를 s평면상에 신속하게 나타낼수있음

- 폐루프 제어 시스템의 안정도와 과도응답 성능 변화를 시작적으로 파악가능

=> 제어기 설계를 용이하게 적용할수있음

근궤적 개념

- 근궤적 파라미터 : 시스템에서 관심갖는 파라미터

- 폐루프 특성방정식

 - 개루프 전달함수 G(s)의 크기와 위상

- 개루프 전달함수 G(s)의 크기 조건식과 위상 조건식을 만족시키는 복소 변수 s

-> 폐루프의 특성방정식

개루프 전달함수의 예시에 따른 폐루프 극점

- k의 변화에 따른 극점의 변화는 우측과 같음

폐루프 극점 s=-1+j에 대응하는 K값(크기 조건식 활용)

근궤적상 점 p

- 위상 조건식을 만족해야 한다 -> theta_1 + theta_2 = 180

Matlab 상 근궤적 그리기

- 다음 근궤적을 보고 적절한 K 값을 설정해야함

선형화없이 비선형 모델을 해석하는방법?

-> 비선형 시스템 동적 분석후 운동방정식 찾기

-> 운동방정식 -> 상태변수 -> 상태방정식

비선형 시스템 모딜렝

-시스템 운동범위나 파라미터 시간 변화에 대한 제약 없이 시스템 특성 그대로 모델링

* 선형화한 경우 동작점 부근에서만 동작한다고 가정하여 모델링 (특정 구간에서만)

- 특수한 상황이나 가정이 없는 상태에서 시스템의 동적 특성을 나타냄

- 해가 존재하지 않는 경우 수치해적적 기법을 이용하여 시스템의 동적 특성을해석해야함

정전기력이 작용하는 질량-스프링- 댐퍼 시스템의 모델링

m

- 고정된 두 벽사이에 전기가 통하는 판(질량)

- 윗벽과 댐퍼와 스프링으로 연결됨

- 전기를 통하는 아래벽 사이에 입력 전압 V_in에 의해 생기는 정전기력(인력)을 받고 있음

-> 전기가 흐르면 정전기력에 의해 아래의 벽이 m을 끌어당기게됨

=> 정진기력에 의해 생기는 질량의 동적 특성을 모델링 하고자함

- 입력 전압 v_i에 의해 간격이 g인 두 도체(m과 아래 벽) 사이의 전하량 변화율)

- 전하량 q에 의해 생기는 정전기력 F

-기계 시스템의 운동 방정식

상태 변수

- q : 전하량

- g : 두 도체간 간격

- q_dot : 간격의 변화율

상태 방정식

- 선형 모델링만 가능한 전달함수와 달리 상태 방정식을 사용하면 비선형 모델링이 가능

비선형 상태방정식의 선형화

- 가정 1. 상태 방정식 상태변수 x와 비선형 함수 u

 -> x_0, u_0에서 선형화

- 가정 2. 선형화 시키려는 지점에 미소한 섭동이 있을때

 -> delta x, delta u 정의

선형화 하려는 지점에서 테일러 급수를 취한 후 선형인 항만 취할때

Jacobian's of f(x.u)

- 앞의 선형 상태방정식을 정전기력이 작용하는 질량 스프링 댐퍼 시스템에 적용하면, f(x,u)에 대한 자코비안은 상태방정식의 A, B 행렬이 됨

정전기력이 작용하는 질량-스프링-댐퍼 시스템의 특성방정식 계수

입력 V_in, 상태 변수 x1, x2, x3이 일정하고 모두 정상상태일때

- 시간에 대한 미분은 모두 0

- 3개의 상태 방정식 -> 2개의 비선형 다항식

-비선형 다항식은 x_1의 3차 다항식이므로 3개의 근을 가짐

- x3은 정상상태를 가정하므로 0임

- V_in 증가에 따라 전하량 charge와 간격 gap(질량 m의 변위)의 변화

V_in이 처음 100초간 0V에서 0.037V 까지 램프 입력으로 증가하고,

그 후 100초간 0.07V에서 0V로 선형 감소하는 경우 각 상태편수들의 과도 응답

비선형 시스템에 대한 비선형 모델링의 한계와 방안

- 시스템 동작에 대한 정확한 정보를 주지만, 모델링이 선형 모델링에 비해 어려움

- 파라미터의 영향력(ex- 스프링 계수) 분석이 선형 모델에 비해 용이하지 않음

=> 선형 모델을 이용해 파라미터 세팅이나 민감도 분석 후 비선형 모델로 효과를 검증하는 것이 좋음

제어시스템 -> 비선형 시스템이 많음

비선형 시스템

- 중첩의 원리를 만족하지 않음

- 입력 크기에 따라 시스템 특성이 변화함

- 설계가 힘들고 사용범위가 제한적임

=> 비선형 시스템을 선형 시스템으로 변환하여 사용 ( 비선형 시스템의 선형화)

선형 시스템 - 직선 

- 중첩의 원리 : 만족

- 시스템 특성 파악 시 입력 크기 고려 필요

비선형 시스템 - 곡선

- 중첩의 원리 : 불만족

- 시스템 특성이 시스템 입력의 크기에 따라 변함

- 해설 및 설계 기법이 어렵고 사용 범위가 제한

- 비선형 시스템을 해석을 위해 특정 구간에 대해 선형화하여 선형 제어 기법을 적용함

테일러 급수의 활용

- 입출력 관계에서 미분이 불가능한 점이 존재하지않는 비선형 시스템에 적용

x_0 근처에서 테일러 급수 이용

v_0 근처에서 선형화한 상태방정식 구하기

- 상태변수 v, 입력 f에 대해 g(s)=v(s)/f(s) 구하기

피드백을 이용한 선형화 - 유체탱크 시스템

- 지정된 수위 h_d가 유지되도록 하는 적절한 제어입력 u(t) 선정

* 유체탱크 및 파이프 단면적은 각각 A와 a로 일정

유체 탱크 시스템의 동적 모델링

1. 작동 범위가 충분히 작을때

- 작동 범위가 h_0 근처일때 테일러 급수로 선형화

2. 작동 범위가 클때

- 피드백 선형화 기법 적용해야함 * 비선형 제어법칙식

피드백 선형화를 위한 제어 시스템 구조

역진자-차량 시스템의 선형화

- 역진자-차량 시스템에 대해 비선형 운동 방정식을 구하고, 평형상태에서 미소운동을 한다는 가정하에 선형 방정식을 구하시오

* 평형 상태 : theta=theta_dot = z_dot= F = tou =0, z=z0

무게 중심에서 막대의 회전관성 J

역진자-차량 시스템의 자유물체도

역진자의 수평, 수직, 회전운동 및 차량의 수평 운동에 대한 운동 방정식

1) 막대기 수평운동

2) 막대기 수직운동

3) 막대기 회전 운동

4) 차량에 대한 수평 운동

수평과 회전 운동에 대한 운동방정식으로 정리 (H(t)와 V(t) 제거)

sin(theta) ~ theta, cos(theta) ~ 1을 대입하여 선형화된 운동방정식 구하기(평성상태서 theta는 0에 가까움)

상태방정식 정리

스탭 응답 구하기

- m =1, g=9.8, M=10, L=1

- 특성 방정식의 근이 +- 2.8을 보임. 양의 값이 존재 -> 불안정 시스템

토크 입력이 없는 경우

- 역진자 차량의 막대가 쓰러짐

제어 성능 및 안정도 평가

- 제어 성능에 대한 객관적인  평가

최적의 제어 성능을 구하는 방법

- 시스템 파라미터 선정시 오차를 이용한 함수 활용 -> 성능 지수

성능 지수

- 최적의 성능을 얻기위해 정한 오차를 이용한 함수

- 시스템 파라미터 선정에 이용

최적 파라미터 선정

- 시스템 성능을 수학적으로  표현가능한 성능지수를 이용하여 최적의 시스템 파라미터 구함

일반적인 성능 지수

- 스텝 입력에 대한 오차e(t)의 제곱을 적분한값

- 오차의 제곱과 성능의 관계 : y_ss와 과도응답 성능을 보여주는 지표 -> 오차

=> 에러의 합이 작을수록 성능이 높다고 볼수 있음

* e^2인 이유 : 음수도 있을수 있기 때문에 상쇄를 방지하기 위함

*성능 지수는 양의 값을 갖는다.

최적의 파라미터 선정 과정

- 파라미터 조정을 통해서 성능지수가 가장 낮은 값을 갖도록 파라미터를 찾음

조정 가능한 피드백 제어 시스템의 폐루프 전달함수

- 게인 K를 어떻게 선정해야 시스템 성능에 유리한가?

-> 성능지수를 이용

제어 시스템의 성능 지수 계산

1. e(s) 계산

2. (스텝입력에대한) 성능지수 공식에 대입

최적 파라미터 k값 선정

- 성능 지수의 미분이 0이 되는 지점 찾기

=> 성능 지수를 정의하여 성능 지수를 최소화하는 게인 값(파라미터)을 찾을수 있다.

과소 감쇠 단순 2차 시스템의 폐루프 전달함수

감쇠비 zeta값에 따른 기타 성능 지수

- e^2은 에러가 크면 에러가 크게 반영

- |e| 시간에 대해 에러를 균등하게 반영

성능지수 I_s의 특징

- 최소 영역이 비교적 넓음

 -> 파라미터 변동에 민감하지 않음

- 수학적 처리가 용이

 -> 실제 제어 시스템 설계시 바람직한 함수

감쇠비 zeta값에 따른 성능지수 비교

선형 시스템의 안정도 판별법

- 안정된 선형 시스템 : 한정된 시스템 응답을 갖는 시스템

-> 시스템에 한정된 입력 or 외란이 가해졌을때 그 응답의 크기가 한정된됨.

* 한정의 의미 : 수렴이 되지 않더라도 값이 어느 범위 안에 머무름을 의미

- 특성방정식의 양의 실수부를 갖는 근의 존재 유무로 판별

* 양의 실수부가 있으면 불안정/없으면 안정 시스템

단위 스텝 입력을 가했을때 출력과 역라플라스변환

특성 방정식의 근 p_i의 실수부 조사

- 시스템 안정도는 특성방정식의 극접 위치 pi에 의해 결정

Routh 안정도 판벌볍

- 수작업으로 안정도 판별 시 사용

- 필요 조건 : 특성방정식의 모든 계수가 같은 부호

- 충븐 조건 

   Routh 배열의 첫 번째 열의 모든 계수가 같은 부호여야 함, 불안정학 극점 개수

전달함수 G(s)로 표현되는 시스템의 안정도와 시간 대역 성능평가

- roots 함수로 특성방정식의 근 계산

제어시스템 성능 평가

- 과도 응답

- 정상상태 응답

제어시스템의 감도

- 플랜트 모델의 불확실성이나 변화에 대해 시스템 성능이 변화하는 정도(민감도)

파라미터 변화에 따른 성능(정상상태오차) 변화 계산

1) 공칭 시스템

2) 시스템 파라미터 변동 1

3) 시스템 파라미터 변동 2

4) 센서 게인 변동

1) 공칭 시스템의 전달함수

정상상태 오차 steady state error

- 최종값 정리 final value theorem : 시간 t를 무한대로 보낼때 error값의 상태

2) 시스템 파라미터의 변동

- 전달함수와 정상상태 오차 계산

 -> k1이 커질수록 에러가 커진다

3) 시스템 파라미터의 변동 2

- k2가 커질수록 에러가 줄어든다

4) 센서 게인 변동

개루프 및 피드백 제어 시스템의 외린 제거 성능 비교

- disturbance가 정상상태 오차에 어떻게 영향을 주는지 봄

1) 개루프 제어 시스템

2) 피드백 제어 시스템

개루프 제어 시스템 외란에 대한 전달함수와 단위 스텝 응답의 최종값

- 1이란 스탭 입력(외란)이 들어올때 반(1/2)만큼 영향을 받음

피드백 제어 시스템 외란에 대한 전달함수와 단위 스텝 응답의 최종값

- 개루프 제어에서 외란이 1일때 1/2만큼 영향을 받던것과는 달리 k가 클수록 외란에 대한 출력이 0으로 수렴한다.

=>

- 외란제거성능 향상

- 큰 제어량이 요구

- 엑추에이터 값이 포화 문제 발생 가능

과도 응답

- 시간이 0부터 일정시간 경과되는 동안 안정화 되기까지 시스템의 응답

과도 응답 성능 평가

- 표준 입력 신호에 대한 시간 응답으로 과도 응답 성능 평가

- 표준 시험 입력 신호 : 임펄스 함수, 스텝 함수, 램프 함수, 가속도 함수, 사인파 함수

임펄스 응답

스텝 응답

- 동적 시스템의 시간 영역 성능 평가에서 가장 많이 사용되는 응답

- 발생시키고 평가하기 가장 쉬운 신호

퍼센트 오버슈트 P.O

-과도 상태 중 정상상태 응답 y_ss를 초과하여나타나는 출력의 최대 오버슈트 M_p를 정상상태 응답 y_ss로 나눈 백분률

* y_p : 출력의 시간응답 최댓값

* 최댓값 시간 t_p : y_p될때 시간

 지연시간 t_d delayed time

- 정상상태응답 y_ss의 50%에 도달하는데 소요되는 시간

상승시간 t_r rising time

- 과대감쇠 시스템(zeta >1) : 정상상태응답 y_ss의 10~90% 상승하는 시간

- 과소감쇠 시스템(0<zeta<1) : 정상상태응답 y_ss의 0~100% 상승하는 시간

정착 시간 t_s settling time

- 출력의 크기가 정상상테 응답의 y_ss의 (delta)%이내로 정착하는데 소요되는 시간

- 일반적으로 사용되는 (delta)값은 2

단순 1차 시스템의 전달함수

시정수(Time constant) T

- 감쇠 정도를 나타내는 지수함수가 e^-1=0.368이 되는 시간 -> y(t)=0.632에 얼마나 빨리도달하는지

- 시정수가 짧을수록 빨리 최종값(정상상태 응답)에 도달

단순 2차 시스템의 전달함수

제어 시스템의 응답 성능

- 제어 시스템의 응답 성능은 과도 응답뿐만이 아니라 정상상태응답 성능도 동시에 만족해야함

- 정상상태 응답 성능은 입력 및 시스템 형태에 따라 판정함

* 시간이 지났을때도 정상상태 오차가 0으로 가는지 or 최소한으로 줄어드는지

단위 스텝 입력에 대한 폐루프 제어 시스템의 정상상태 오차

폐루프 제어 시스템의 정상상태 오차 크기

- 개루프 전달함수 G(s)의 형태에 따라 결정

- G(s)를 아래와 같이 정의할때 어떻게 G(0)의 변화를 봄

제 0형 시스템(N=0)의 정상상태 오차

- k_p는 G(s)의 분자 성분

n>=1 일때 스탭 입력에 대한 정상상태 오차

- e_ss = 0

DC 모터 제어시스템의 스텝 기준 및 외란 입력에 대한 시스템 형태와 정상상태 응답 특성

1) 비례 피드백 제어 시스템

2) 단위 피드백 제어 시스템

비례 피드백 제어 시스템의 폐루프 전달함수 T(s)와 오차 e(s)

단위 스텝 기준 입력 r(s)에 대한 정상상태 오차

- 비례 피드백(k != 1) 제어 시스템(제 0형 시스템) -> 정상상태 오차 발생

- 단위 피드벡 제어 시스템(제1형시스템) -> 정상상태오차 = 0

단위 스텝 외란 입력에 따른 정상상태 응답

- 단위 피드백 제어 시스템의 스텝 외란-출력 전달함수

=> 외란의 영향을 완전히 제거할수 없음

* 단위 스텝 외란에 대해 제 0형 시스템

강체 rigid body

- 형태와 크기가 변하지 않는 단단한 물체

두 강체의 동적 시스템

- 기계 시스템 : 다강체 시스템인 경우가 많음

-> 강체간 상호작용을 이해하는데 필요

두 강체 동적 시스템 정의

- 두 강체가 스프링 같은 에너지 저장요소와 댐퍼 같은 에너지 소비요소로 연결된 시스템

- 제어 대상이되는 기계시스템은 모델링 할대 둘 또는 그 이상인 다강체 시스템인 경우가 많음

- 두 강체 시스템 모델링은 강체간 상호작용을 이해하는데 중요

(1) 두 강체 시스템 질량 m1에 가해지는 외력을 입력으로 하고, 두 질량에 대한 운동방정식을 구해보자

1) m1에 대한 자유물체도와 운동역학 선도를 구함

- m1에는 스프링과 댐퍼로부터 힘 F에 반대되는 힘이 작용됨

2) m2에 대한 자유물체도와 운동역학선도

- k1, b1은 m1에 대한 반력이 되나 m2에 대해서는 정방향으로 작용

3) 두식을 정리

4) 라플라스 변환 - 전달함수 구하기

- z1에 대해 정리한 식 2를  식 1에 대입하여 입력 F에 대한 출력 z2의 전달함수를 구할수 있다

-

상태 공간을 이용한 시스템 모델링

- 아래의 운동방정식으로 상태 공간으로 시스템 모델링해보자

- 다음의 경우에 대해 상태 공간을 구하자

m1 = 10, b1=20, k1=100, m2=1, b2=20, k2=100

임펄스 응답 구하기

- z1이 감소 감쇄가 보임 -> 0으로 수렴

스탭 응답

- z1는 과소감쇄를 보이며 0.02로 수렴

- z3은 0.01로 수렴

초기 조건이 있는 경우 응답

- z1이 1이고 나머지는 0인 경우 응답 -> z1이 1에 시작하여 제자리로 돌아감

상태공간 state space

- 지정된 시간에서 시스템 상태를 완전히 서술하는데 필요한 변수 집합

- 시스템 상태를 명확히 정의할수있음

- 초기조건이 있는경우에도 사용 가능

상태 변수 state variable

- 상태를 정의할수있는 임의의 최소 변수

상태 변수 state vector

- 상태 변수들의 벡터형태 표현

상태 공간 모델링 state space model

- 상태 방정식과 출력 방정식을 아래와 같이 표현

상태 방정식 state equation

- 상태변수의 시간에 대한 변화율 xdot이 상태변수 x(상태전이행렬 A)와 입력 u(입력 행렬 B)와 어떤 관계를 갖는가

- 일차 선형 미분방정식으로 표현

- 선형 시불변 다변수 시스템인 경우

출력 방정식 output equation

- 출력이 상태변수 x(output행렬 c)와 입력(D)와 어떤관계를 갖는가

- 선형 미분방정식으로 표현

- 선형 시불변 다변수 시스템의 경우

상태변수 선정

- 시스템 내에 독립된 에너지 저장요소 변수

- 위치 에너지 저쟝요소의 작용력 변수와 운동에너지 저장요소의 흐름 변수

- 위치 에너지 저장요소의 일반화된 변위변수와 운동에너지 저장요소의 일반화된 속도변수

- 시스템 상태와 밀접한 관계를 갖는 변수

질량-스프링-댐퍼 시스템의 상태변수

- 함 F와 속도 xdot

- 변위 x와 속도 xdot

전달함수와 상태공간 비교

상태 공간의 장점

- 컴퓨터가 상대적으로 식 연산하기 쉬움

- 상태에 대한 정의가 명확

- 초기 조건이 있는 경우도 가능(TF는 초기 조건 0으로 가정)

- 다변수 입력, 다변수 출력 가능 MIMO

- 시변, 비선형 시스템 모델링도 가능

- S-domain 갈 필요없음

질량-스프링-댐퍼 시스템 상태공간 모델링

상태 공간 표현

-질량-스프링-댐퍼 시스템 :  m=1, b=20, k=100

질량-스프링-댐퍼 시스템 임펄스 응답

출력 변경

- 이전에는 변위만 출력

- C를 변경하여 변위와 속도 둘다 출력

- y1는 변위 출력, y2 속도 출력

상태 공간에 초기 조건이 주어진 경우

- 명령어 initial 사용

- initial(상태공간모델, 초기조건)

- 아래는 변위 1, 속도 3의 초기조건

스탭응답구하기

- step(상태공간)