제어 성능 및 안정도 평가
- 제어 성능에 대한 객관적인 평가
최적의 제어 성능을 구하는 방법
- 시스템 파라미터 선정시 오차를 이용한 함수 활용 -> 성능 지수
성능 지수
- 최적의 성능을 얻기위해 정한 오차를 이용한 함수
- 시스템 파라미터 선정에 이용
최적 파라미터 선정
- 시스템 성능을 수학적으로 표현가능한 성능지수를 이용하여 최적의 시스템 파라미터 구함
일반적인 성능 지수
- 스텝 입력에 대한 오차e(t)의 제곱을 적분한값
- 오차의 제곱과 성능의 관계 : y_ss와 과도응답 성능을 보여주는 지표 -> 오차
=> 에러의 합이 작을수록 성능이 높다고 볼수 있음
* e^2인 이유 : 음수도 있을수 있기 때문에 상쇄를 방지하기 위함
*성능 지수는 양의 값을 갖는다.
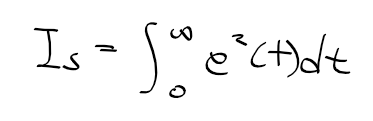
최적의 파라미터 선정 과정
- 파라미터 조정을 통해서 성능지수가 가장 낮은 값을 갖도록 파라미터를 찾음

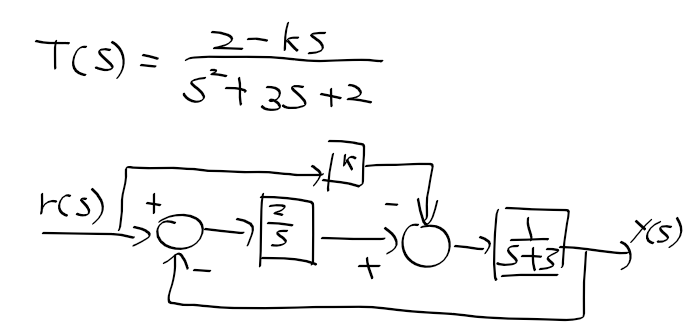
조정 가능한 피드백 제어 시스템의 폐루프 전달함수
- 게인 K를 어떻게 선정해야 시스템 성능에 유리한가?
-> 성능지수를 이용
제어 시스템의 성능 지수 계산
1. e(s) 계산
2. (스텝입력에대한) 성능지수 공식에 대입
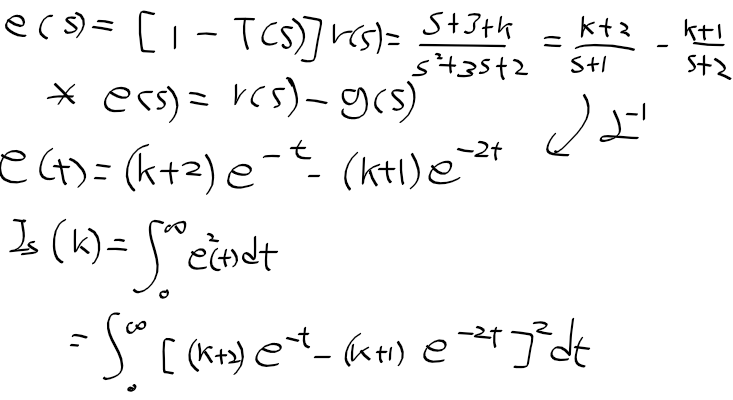
최적 파라미터 k값 선정
- 성능 지수의 미분이 0이 되는 지점 찾기
=> 성능 지수를 정의하여 성능 지수를 최소화하는 게인 값(파라미터)을 찾을수 있다.

과소 감쇠 단순 2차 시스템의 폐루프 전달함수

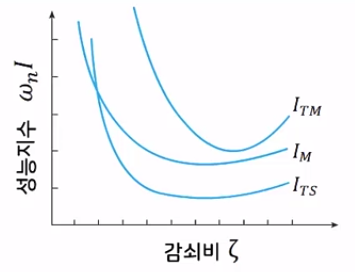
감쇠비 zeta값에 따른 기타 성능 지수
- e^2은 에러가 크면 에러가 크게 반영
- |e| 시간에 대해 에러를 균등하게 반영
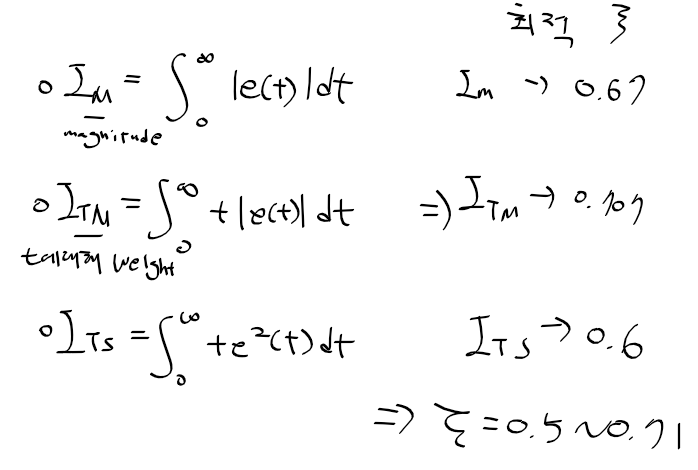
성능지수 I_s의 특징
- 최소 영역이 비교적 넓음
-> 파라미터 변동에 민감하지 않음
- 수학적 처리가 용이
-> 실제 제어 시스템 설계시 바람직한 함수
감쇠비 zeta값에 따른 성능지수 비교

선형 시스템의 안정도 판별법
- 안정된 선형 시스템 : 한정된 시스템 응답을 갖는 시스템
-> 시스템에 한정된 입력 or 외란이 가해졌을때 그 응답의 크기가 한정된됨.
* 한정의 의미 : 수렴이 되지 않더라도 값이 어느 범위 안에 머무름을 의미
- 특성방정식의 양의 실수부를 갖는 근의 존재 유무로 판별
* 양의 실수부가 있으면 불안정/없으면 안정 시스템
단위 스텝 입력을 가했을때 출력과 역라플라스변환
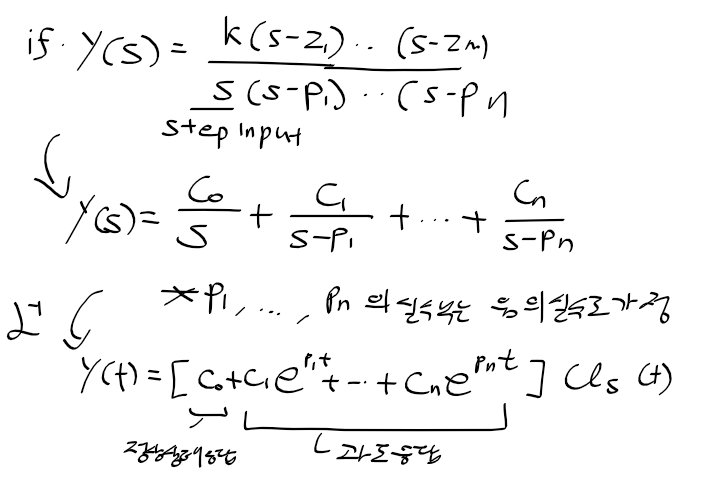
특성 방정식의 근 p_i의 실수부 조사
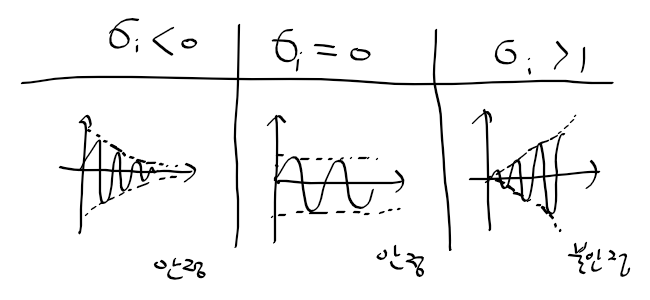
- 시스템 안정도는 특성방정식의 극접 위치 pi에 의해 결정

Routh 안정도 판벌볍
- 수작업으로 안정도 판별 시 사용
- 필요 조건 : 특성방정식의 모든 계수가 같은 부호
- 충븐 조건
Routh 배열의 첫 번째 열의 모든 계수가 같은 부호여야 함, 불안정학 극점 개수
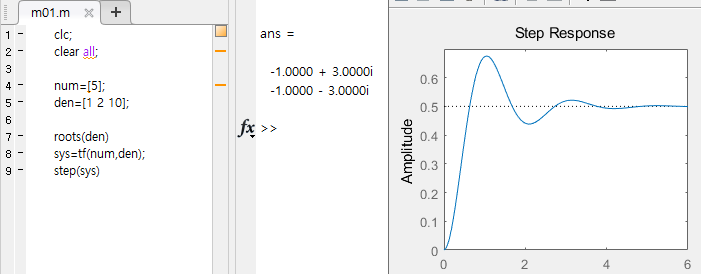
전달함수 G(s)로 표현되는 시스템의 안정도와 시간 대역 성능평가

- roots 함수로 특성방정식의 근 계산
'로봇 > 제어' 카테고리의 다른 글
| 제어공학 2 -12 비선형 모델링 및 해석 (0) | 2020.05.09 |
|---|---|
| 제어공학 2 - 11 비선형 모델의 선형화 (0) | 2020.05.09 |
| 제어공학 2 - 9 과도응답 및 정상상태 응답 (0) | 2020.05.09 |
| 제어공학 2 - 7 두 강체의 동적 시스템 (0) | 2020.05.09 |
| 제어공학 2 - 6 상태공간 (0) | 2020.05.08 |