비례제어 proportional control
- 오차 x 적절한 크기 이득 = 플랜트 입력
- 근궤적을 이용해 이득 결정
비례제어이득을 갖는 폐루프 시스템
- 에러에 상수 k_p를 곱하여 G(s)의 인풋으로 사용되는 시스템

개루프 시스템
- 입력에 대한 시스템 출력 응답 G(s)의 특성방정식 근들중 근의 실수부가 허수축에 가까운 근의 위치에 의해 결정됨

폐루프 시스템
- 입력에 대한 시스템 출력 응답은 T(s)의 특성방정식 근중 실수부가 허수축에 가까운 근의 위치에 의해 결정됨

- kp에 의해 특성방정식 근의 위치가 변할 수 있음.

G(s) 특성방정식의 근
- 개루프 전달함수 극점들의 변경이 필요할 때
-> 플랜트 파라미터 변경이 필요

T(s)의 특성방정식 근
- k_p를 이용해 제한적이지만 근의 위치를 변경가능
-> 플랜트 파라미터 변경이 불필요함

비례 제어 시스템 해석
비례 제어
- 기준값 r(s)와 출력의 오차인 e(s)에 이득 k_p을 곱한 값을 제어 대상인 플랜트의 입력 u(s)로 하는 제어기법
- 오차에 비례한 값이 플랜트의 입력이 되므로 비례제어라 함
비례제어와 근궤적과의 관계
- 비례제어 효과 : 근궤적으로부터 예측 가능함
- 비례제어 이득 결정 방법 ; 근궤적으로부터 시스템이 원하는 정상상태응답과 과도응답 특성을 나타내는 이득을 정하게됨
비례시스템 예제
- 영점 : -4
- 극점 : 3개 -> -6, 복소수 극점 2개


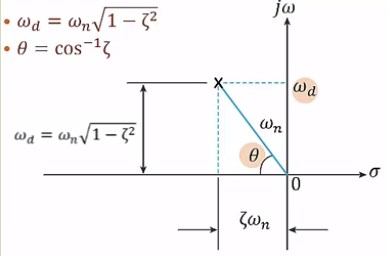
theta 값으로 감쇄비를 알수 있음
근의 실수부 크기 = zeta * 고유 진동수 w_n
감쇄비 허수축 크기 = 감쇄 고유주파수 w_d
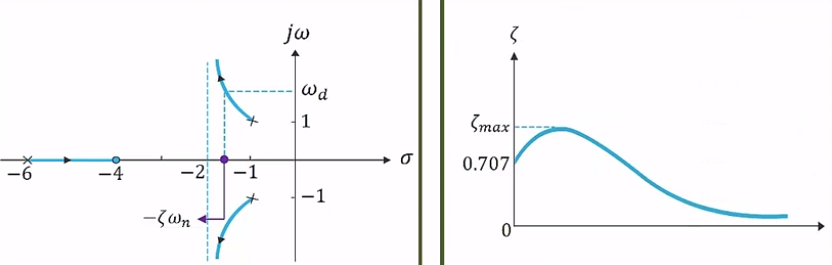
1. 허수축에 가까운 두 극점 위주로 보아야 함
2. 감쇄비의 변화를 보면 어느 시점에서 최대(zeta_max)가 되고 0으로 수렴
폐루프 시스템의 정상상태 오차
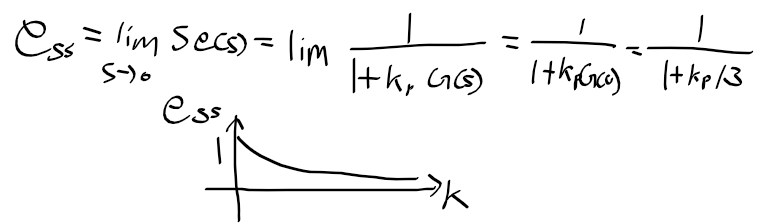
개루프 시스템과 비례제어이득이 k_p=28.3인 폐루프 시스템의 스텝응답
1) 개루프 시스템의 스텝 응답
- 수렴하는 값이 0.333 이므로 e_ss=0.667
- P.O = 4.8%
- T_s = 4.11초

2) 폐루프 시스템의 스텝응답 K_p=28.3
- 수렴하는 값은 0.904로 스텝입력 1과 e_ss = 0.096의 정상상태 오차를 보임
- PO는 40.5%
- T_s=2.16초 나타남
- 과소 감쇄 형태

폐루프 시스템의 스텝응답 (k_p=1)
- 수렴하는 값은 0.25로 스텝입려 1과 e_ss=0.75 정상상태 오차를 보임
- PO는 8.0%
- T_s=3.57초



근궤적 1
- 극점 -6에서 시작할때 게인이 무한대로 증가할때 근은 영점인 -4에 가까워짐
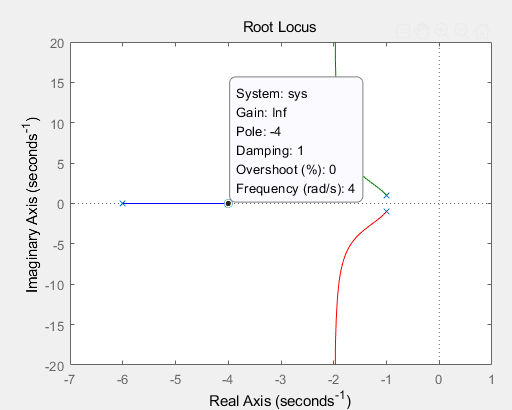
근궤적 2. 게인이 0인 경우
- 댐핑비 : 0.707
- 퍼센트 오버슈트: 4.32
- 자연주파수 : 1.41
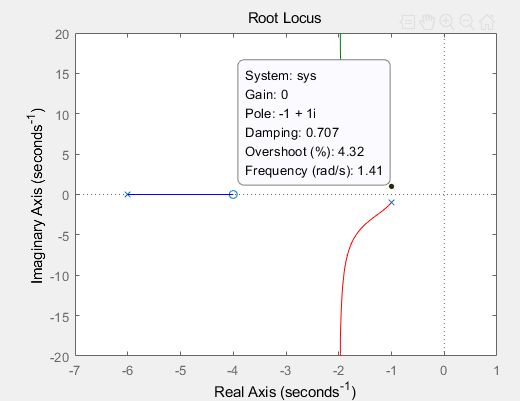
근궤적 2
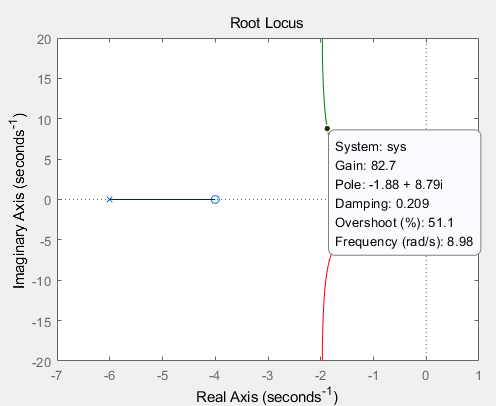
- 근 -1+j에서 시작하여 게인 값이 증가할때 근의 실수부는 -2에 가까워지고, 허수부는 점점 증가
'로봇 > 제어' 카테고리의 다른 글
| 제어공학 2 - 16 근궤적법을 이용한 앞섬 보상기 설계 (0) | 2020.05.10 |
|---|---|
| 제어공학 2 - 15 근궤적법을 이용한 비례적분미분 제어기 (0) | 2020.05.10 |
| 제어공학 2 - 13 근궤적법 (0) | 2020.05.09 |
| 제어공학 2 -12 비선형 모델링 및 해석 (0) | 2020.05.09 |
| 제어공학 2 - 11 비선형 모델의 선형화 (0) | 2020.05.09 |