선형화없이 비선형 모델을 해석하는방법?
-> 비선형 시스템 동적 분석후 운동방정식 찾기
-> 운동방정식 -> 상태변수 -> 상태방정식
비선형 시스템 모딜렝
-시스템 운동범위나 파라미터 시간 변화에 대한 제약 없이 시스템 특성 그대로 모델링
* 선형화한 경우 동작점 부근에서만 동작한다고 가정하여 모델링 (특정 구간에서만)
- 특수한 상황이나 가정이 없는 상태에서 시스템의 동적 특성을 나타냄
- 해가 존재하지 않는 경우 수치해적적 기법을 이용하여 시스템의 동적 특성을해석해야함
정전기력이 작용하는 질량-스프링- 댐퍼 시스템의 모델링
m
- 고정된 두 벽사이에 전기가 통하는 판(질량)
- 윗벽과 댐퍼와 스프링으로 연결됨
- 전기를 통하는 아래벽 사이에 입력 전압 V_in에 의해 생기는 정전기력(인력)을 받고 있음
-> 전기가 흐르면 정전기력에 의해 아래의 벽이 m을 끌어당기게됨
=> 정진기력에 의해 생기는 질량의 동적 특성을 모델링 하고자함

- 입력 전압 v_i에 의해 간격이 g인 두 도체(m과 아래 벽) 사이의 전하량 변화율)
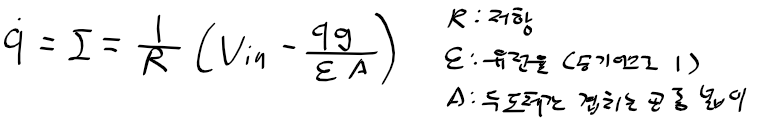
- 전하량 q에 의해 생기는 정전기력 F
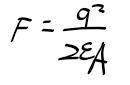
-기계 시스템의 운동 방정식

상태 변수
- q : 전하량
- g : 두 도체간 간격
- q_dot : 간격의 변화율

상태 방정식
- 선형 모델링만 가능한 전달함수와 달리 상태 방정식을 사용하면 비선형 모델링이 가능
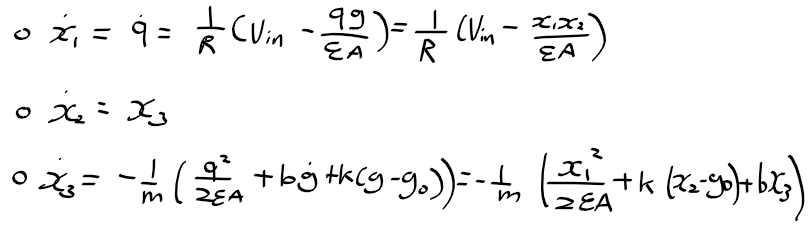
비선형 상태방정식의 선형화
- 가정 1. 상태 방정식 상태변수 x와 비선형 함수 u
-> x_0, u_0에서 선형화

- 가정 2. 선형화 시키려는 지점에 미소한 섭동이 있을때
-> delta x, delta u 정의
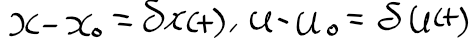
선형화 하려는 지점에서 테일러 급수를 취한 후 선형인 항만 취할때

Jacobian's of f(x.u)
- 앞의 선형 상태방정식을 정전기력이 작용하는 질량 스프링 댐퍼 시스템에 적용하면, f(x,u)에 대한 자코비안은 상태방정식의 A, B 행렬이 됨

정전기력이 작용하는 질량-스프링-댐퍼 시스템의 특성방정식 계수
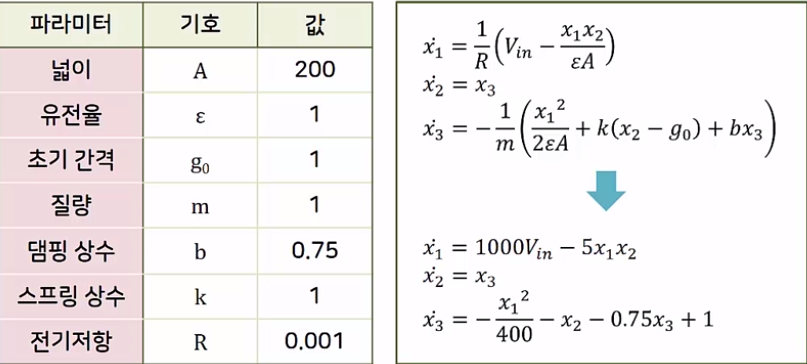
입력 V_in, 상태 변수 x1, x2, x3이 일정하고 모두 정상상태일때
- 시간에 대한 미분은 모두 0
- 3개의 상태 방정식 -> 2개의 비선형 다항식

-비선형 다항식은 x_1의 3차 다항식이므로 3개의 근을 가짐
- x3은 정상상태를 가정하므로 0임

- V_in 증가에 따라 전하량 charge와 간격 gap(질량 m의 변위)의 변화

V_in이 처음 100초간 0V에서 0.037V 까지 램프 입력으로 증가하고,
그 후 100초간 0.07V에서 0V로 선형 감소하는 경우 각 상태편수들의 과도 응답


비선형 시스템에 대한 비선형 모델링의 한계와 방안
- 시스템 동작에 대한 정확한 정보를 주지만, 모델링이 선형 모델링에 비해 어려움
- 파라미터의 영향력(ex- 스프링 계수) 분석이 선형 모델에 비해 용이하지 않음
=> 선형 모델을 이용해 파라미터 세팅이나 민감도 분석 후 비선형 모델로 효과를 검증하는 것이 좋음
'로봇 > 제어' 카테고리의 다른 글
| 제어공학 2 - 14 근궤적법을 이용한 비례제어기 설계 (0) | 2020.05.09 |
|---|---|
| 제어공학 2 - 13 근궤적법 (0) | 2020.05.09 |
| 제어공학 2 - 11 비선형 모델의 선형화 (0) | 2020.05.09 |
| 제어공학 2 - 10 제어성능 및 안정도 평가 (0) | 2020.05.09 |
| 제어공학 2 - 9 과도응답 및 정상상태 응답 (0) | 2020.05.09 |