제어시스템 -> 비선형 시스템이 많음
비선형 시스템
- 중첩의 원리를 만족하지 않음
- 입력 크기에 따라 시스템 특성이 변화함
- 설계가 힘들고 사용범위가 제한적임
=> 비선형 시스템을 선형 시스템으로 변환하여 사용 ( 비선형 시스템의 선형화)
선형 시스템 - 직선
- 중첩의 원리 : 만족
- 시스템 특성 파악 시 입력 크기 고려 필요
비선형 시스템 - 곡선
- 중첩의 원리 : 불만족
- 시스템 특성이 시스템 입력의 크기에 따라 변함
- 해설 및 설계 기법이 어렵고 사용 범위가 제한
- 비선형 시스템을 해석을 위해 특정 구간에 대해 선형화하여 선형 제어 기법을 적용함
테일러 급수의 활용
- 입출력 관계에서 미분이 불가능한 점이 존재하지않는 비선형 시스템에 적용
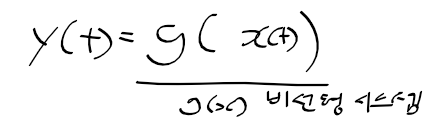
x_0 근처에서 테일러 급수 이용
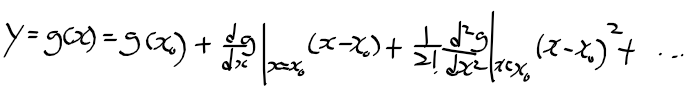

v_0 근처에서 선형화한 상태방정식 구하기
- 상태변수 v, 입력 f에 대해 g(s)=v(s)/f(s) 구하기


피드백을 이용한 선형화 - 유체탱크 시스템
- 지정된 수위 h_d가 유지되도록 하는 적절한 제어입력 u(t) 선정
* 유체탱크 및 파이프 단면적은 각각 A와 a로 일정

유체 탱크 시스템의 동적 모델링
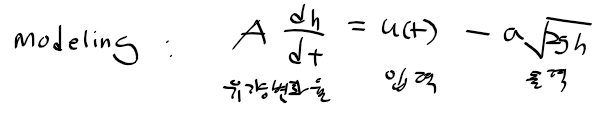
1. 작동 범위가 충분히 작을때
- 작동 범위가 h_0 근처일때 테일러 급수로 선형화

2. 작동 범위가 클때
- 피드백 선형화 기법 적용해야함 * 비선형 제어법칙식

피드백 선형화를 위한 제어 시스템 구조

역진자-차량 시스템의 선형화
- 역진자-차량 시스템에 대해 비선형 운동 방정식을 구하고, 평형상태에서 미소운동을 한다는 가정하에 선형 방정식을 구하시오
* 평형 상태 : theta=theta_dot = z_dot= F = tou =0, z=z0

무게 중심에서 막대의 회전관성 J

역진자-차량 시스템의 자유물체도
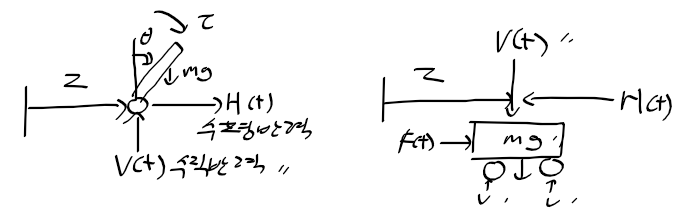
역진자의 수평, 수직, 회전운동 및 차량의 수평 운동에 대한 운동 방정식
1) 막대기 수평운동

2) 막대기 수직운동
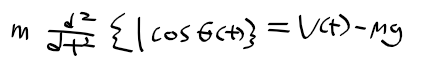
3) 막대기 회전 운동
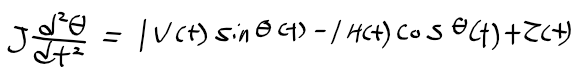
4) 차량에 대한 수평 운동
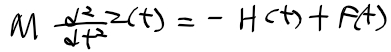
수평과 회전 운동에 대한 운동방정식으로 정리 (H(t)와 V(t) 제거)
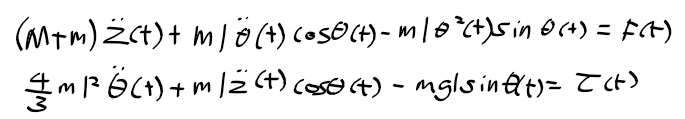
sin(theta) ~ theta, cos(theta) ~ 1을 대입하여 선형화된 운동방정식 구하기(평성상태서 theta는 0에 가까움)

상태방정식 정리

스탭 응답 구하기
- m =1, g=9.8, M=10, L=1
- 특성 방정식의 근이 +- 2.8을 보임. 양의 값이 존재 -> 불안정 시스템

토크 입력이 없는 경우
- 역진자 차량의 막대가 쓰러짐

'로봇 > 제어' 카테고리의 다른 글
| 제어공학 2 - 13 근궤적법 (0) | 2020.05.09 |
|---|---|
| 제어공학 2 -12 비선형 모델링 및 해석 (0) | 2020.05.09 |
| 제어공학 2 - 10 제어성능 및 안정도 평가 (0) | 2020.05.09 |
| 제어공학 2 - 9 과도응답 및 정상상태 응답 (0) | 2020.05.09 |
| 제어공학 2 - 7 두 강체의 동적 시스템 (0) | 2020.05.09 |