질량-스프링-댐퍼 시스템 개요
- 제어 대상물들의 운동 -> 모델링이라는 과정으로 수학적으로 기술되어야함
- 수학적 모델이 필요한 이유 -> 제어 대상물의 운동을 이해해야 제어 설계가 가능함
- 달리는 사람의 무게가 크다면 -> 제동력도 크게 작용해야 원하는 지점에 빨리 멈출 수 있음
- 같은 무게인 경우 -> 달리는 속도/가속도에 따라 제동력이 적절히 결정되어야 함
- 적절한 제어에 필요 한 것 -> 제어 대상의 질량, 스프링 상수, 댐핑 상수 같은 파라미터로 이루어진 운동 방정식
질량-스프링-댐퍼 시스템
- 질량에 스프링과 댐퍼가 병렬로 추가된 시스템

댐퍼의 역활
- 질량/스프링이 가지는 에너지 소모
- 질량의 운동방향과 반대 방향으로 댐퍼에서 힘 작용
- F = 댐핑상수 x 질량 속도
자유물체도 Free body diagram
- 질량 m이 힘 F에의해 x방향으로 변위 x로 xdot의 속도로 움직일때
- 스프링과 댐퍼가 질량에 작용하는 힘을 나타낸것

운동역학선도
- 자유물체도에서 외력 F와 그 반대로 작용하는 두힘 kx와 bxdot이 균형을 이루지 못하는 경우
-> 물체에 관성력 발생
* 관성력 = 질량 x 질량의 가속도
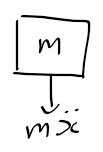
자유물체도와 운동역학선도
- 자유물체도의 힘들과 관성력이 균형을 이루는 경우 물체의 운동 방정식을 구할 수 있음
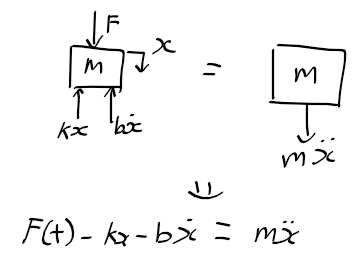
질량 m의 변위를 구하기
- x항만 좌항으로 이동하여 정리하면

- 주어진 F에 대해 다음의 식을 구하면 질량 m의 변위를 구할 수 있음 -> 아래의 식 1, 2의 합
1. F(t)가 0인 경우의 해 -> 동차해
2. F(t)가 0이 아닌 경우의 해 -> 특수 해
동차해의 경우

댐핑 비와 고유진동수

동차해의 경우의 수
- 과도 감쇄(overdamped) : 감쇄비 > 1, 두근이 실수인경우

- 임계 감쇄(critical Damped) : 감쇄비 = 1, 두근이 중근인 경우 -> 진동이 움직임 없이 소멸되는 경우

- 과소 감쇄(Under damped) : 감쇄비 < 1, 두 근이 공액 복소수인경우
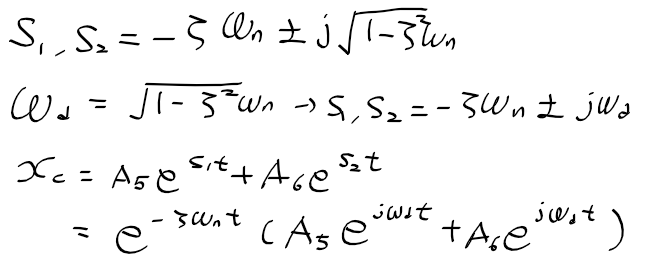
F(t)가 임펄스인 특수해의 경우

-> 두 근이 실수인경우, 중근인 경우, 허근인 경우 구할 수 있음.
- 과도 감쇠 : 감쇄비 > 1, 두 근이 서로다른 음수

- 역라플라스 변환을 하여 시간에 대한 식을 구하고 두 해는 음수 이므로 시간이 증가함에 따라 0으로 수렴

- 임계 감쇄 : 감쇄비 = 1, 두근이 중근인 경우

- 과소 감쇄 : 감쇄비 < 1, 두근이 복소수인경우

- F(t)와 초기 조건이 있는 경우

---------------------------------------
시스템 응답 구하기
1) 외력 F가 0, 초기 조건이 있는 경우
- 댐핑비 = 0(댐핑이 없음), m = 1kg, k = 9N/m, x(0) = 1, xdot(0)=0 가정

- 댐핑비 > 1(과도 감쇠), m = 1kg, b=12Ns/m, k=9N/m, x(0)=1, xdot(0)=0


- 댐핑비 = 1, 중근 -> 임계 감쇄
-> m = 1 kg, b = 6Ns/m, k=9N/m, x(0)=1, xdot(0)=0
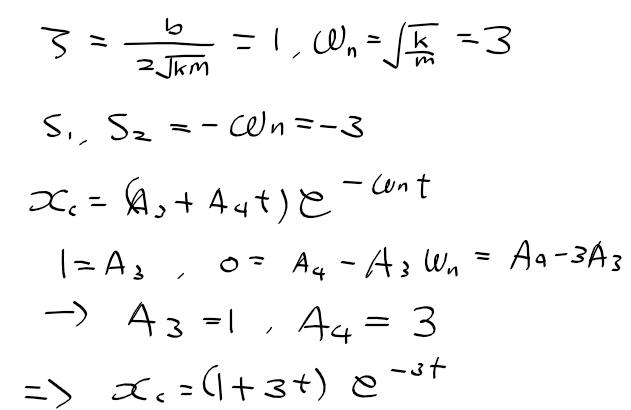

- 과소 감쇄 : 감쇄비 < 1, 허근을 갖는 경우

감쇄비와 해의 비교
1. 댐핑이 없는 경우, 감쇄비 = 0
2. 과도 감쇄, 감쇄비 > 1
3. 임계 감쇄, 감쇄비 = 1
4. 과소 감쇄, 감쇄비 < 1

'로봇 > 제어' 카테고리의 다른 글
| 제어공학 2 - 6 상태공간 (0) | 2020.05.08 |
|---|---|
| 제어공학 2 - 5 전달함수 (0) | 2020.05.08 |
| 제어공학 2 - MATLAB (0) | 2020.05.08 |
| 제어공학 2 - 1 제어공학과 동적 시스템 (0) | 2020.05.07 |
| 제어공학 1 - 제어공학이란 (0) | 2020.05.07 |