주파수 응답
- 주파수 입력에 대한 출력 응답
주파수 입력
- 사인함수처럼 주기적인 신호 입력
주파수 응답
- 시스템에 사인파 입력을 가할때 입력 주파수 omega 값에 따른 입력 진폭에 대한 정상상태에서 출력 진폭비 M(omega), 입력과 출력사이 위상차 phi(omega)
- 시스템 입출력 진폭비 M(omega) = 주파수 전달함수 크기 |G(jw)|
- 시스템 입출력 위상차 phi(omega) = 주파수 전달함수 위상 <G(jw)
* 위상차 입력이 주어졌을 때 출력의 시간 차이
주파수 응답 특성을 나타내는 도해석적 방법
1. bode 선도
- 주파수 omega에 따른 크기와 위상을 직교좌표상에 나타낸 선도
2. Nyquist 선도
- 주파수 omega에 따른 G(jw)의 크기와 위상의 극좌표상에 나타낸 선도
주파수 응답 선도
- 제어시스템의 안정도와 주파수 영역 성능 평가에 필요
주파수 영역에서 전달함수 크기와 위상
- s에 jw를 대입한 후 복소수의 크기와 위상을 구함
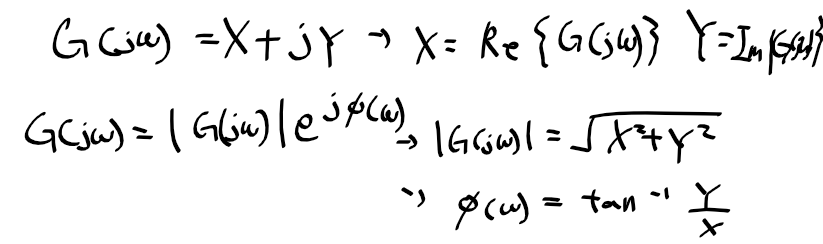

주파수 응답
- 주파수 omega에 따른 주파수 전달함수 크기, M(omega)=|G(jw)|와 phi(omega) = <G(jw)을 나타냄

사인파 입력 u(s), 출력 y(s)
1. u(t) = A sint(wt)를 라플라스 변환하면

2. 다음처럼 변환

3. c, c*를 대입하여 출력 구함

4. 역 라플라스 변환 수행

시스템이 안정된 경우
- y(t)의 둘째 항이후 모든 항은 정상상태 (t->inf)에서 0이 되므로 첫째항만 남음
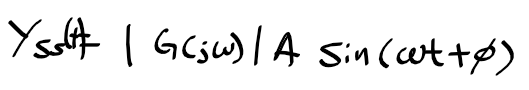
- 출력 진폭 B : 입력진폭 A * |G(jw)| 또는 M(omega)=|G(jw)|=진폭 B/ 진폭 A
- 출력 위상 : 입력 위상 (wt+phi) 또는 phi(omega) = <G(jw)= 입출력 위상차
- 전달함수 G(s)|s->jw : 주파수 전달함수
=> 크기 |G(jw)|와 위상 <G(jw)를 조사하면 주파수 응답 특성을 알 수 있음
전달함수를 이용한 주파수 응답
1. 전달함수의 크기 |G(jw)|와 위상 <G(jw) 조사
-> 주파수 응답 특성이 파악 가능
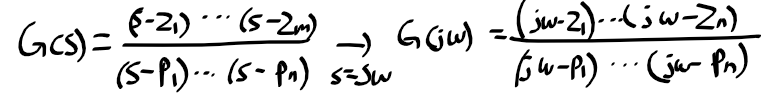
- |G(jw)|의 정의
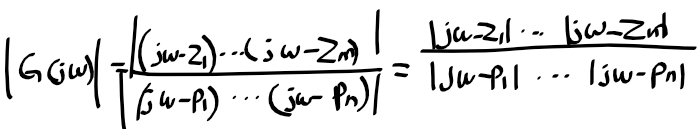
- <G(jw)의 정의

질량-스프링-댐퍼 시스템의 주파수 응답
- F(t)를 입력, x(t)를 출력으로하는 전달함수 G(s)

전달 함수의 두 극점
- m=1, k=9, b=3, zeta=0.5, wn=3(rad/s)
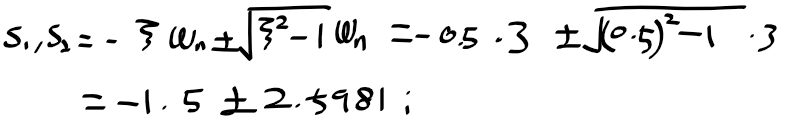
전달함수 G(s)의 크기와 위상
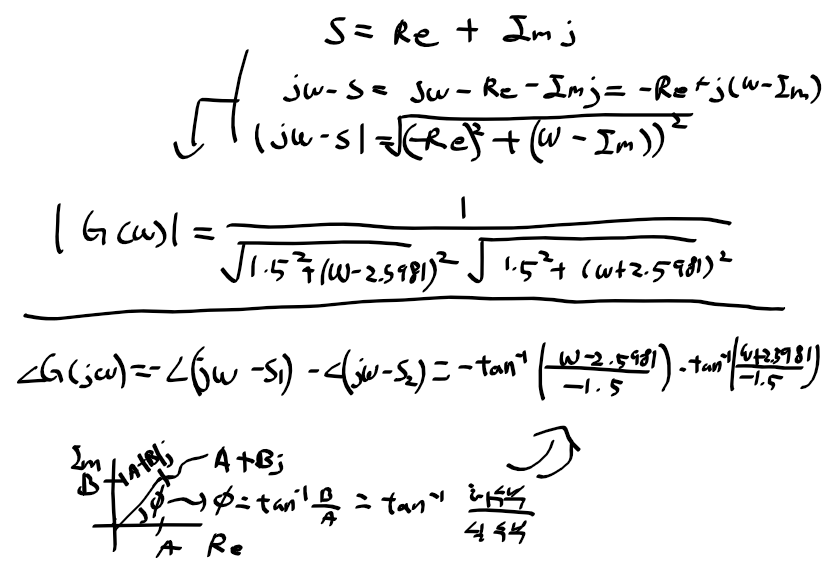
전달함수 G(s)의 크기를 omega=0.1 ~ 100(rad/s) 까지 구하는 경우


'로봇 > 제어' 카테고리의 다른 글
| 제어공학 2 - 20 Nyquist 선도 (0) | 2020.05.11 |
|---|---|
| 제어공학 2 - 19 Bode 선도 (0) | 2020.05.10 |
| 제어공학 2 - 17. 근궤적법을 이용한 뒤짐보상기 설계 (0) | 2020.05.10 |
| 제어공학 2 - 16 근궤적법을 이용한 앞섬 보상기 설계 (0) | 2020.05.10 |
| 제어공학 2 - 15 근궤적법을 이용한 비례적분미분 제어기 (0) | 2020.05.10 |