제어시스템 성능 평가
- 과도 응답
- 정상상태 응답
제어시스템의 감도
- 플랜트 모델의 불확실성이나 변화에 대해 시스템 성능이 변화하는 정도(민감도)
파라미터 변화에 따른 성능(정상상태오차) 변화 계산
1) 공칭 시스템
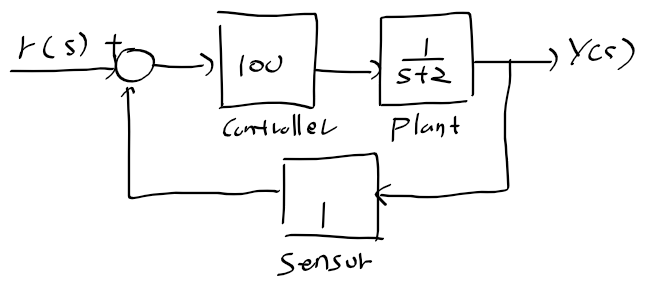
2) 시스템 파라미터 변동 1

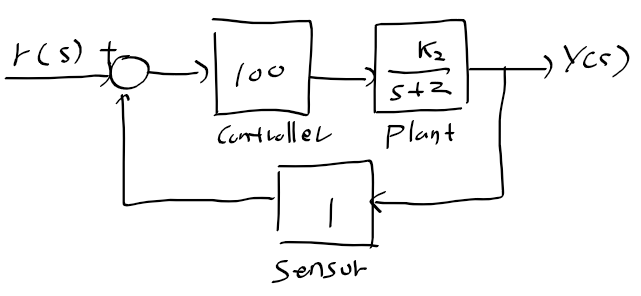
3) 시스템 파라미터 변동 2
4) 센서 게인 변동

1) 공칭 시스템의 전달함수
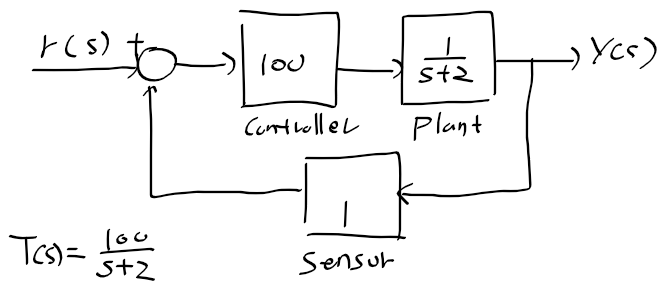
정상상태 오차 steady state error
- 최종값 정리 final value theorem : 시간 t를 무한대로 보낼때 error값의 상태

2) 시스템 파라미터의 변동
- 전달함수와 정상상태 오차 계산
-> k1이 커질수록 에러가 커진다

3) 시스템 파라미터의 변동 2
- k2가 커질수록 에러가 줄어든다

4) 센서 게인 변동

개루프 및 피드백 제어 시스템의 외린 제거 성능 비교
- disturbance가 정상상태 오차에 어떻게 영향을 주는지 봄
1) 개루프 제어 시스템

2) 피드백 제어 시스템

개루프 제어 시스템 외란에 대한 전달함수와 단위 스텝 응답의 최종값
- 1이란 스탭 입력(외란)이 들어올때 반(1/2)만큼 영향을 받음
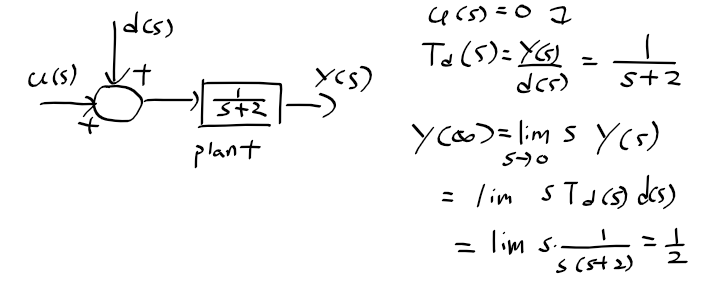
피드백 제어 시스템 외란에 대한 전달함수와 단위 스텝 응답의 최종값
- 개루프 제어에서 외란이 1일때 1/2만큼 영향을 받던것과는 달리 k가 클수록 외란에 대한 출력이 0으로 수렴한다.
=>
- 외란제거성능 향상
- 큰 제어량이 요구
- 엑추에이터 값이 포화 문제 발생 가능


과도 응답
- 시간이 0부터 일정시간 경과되는 동안 안정화 되기까지 시스템의 응답
과도 응답 성능 평가
- 표준 입력 신호에 대한 시간 응답으로 과도 응답 성능 평가
- 표준 시험 입력 신호 : 임펄스 함수, 스텝 함수, 램프 함수, 가속도 함수, 사인파 함수
임펄스 응답
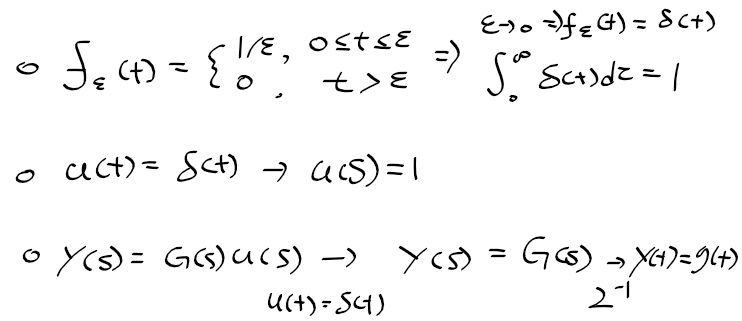
스텝 응답
- 동적 시스템의 시간 영역 성능 평가에서 가장 많이 사용되는 응답
- 발생시키고 평가하기 가장 쉬운 신호

퍼센트 오버슈트 P.O
-과도 상태 중 정상상태 응답 y_ss를 초과하여나타나는 출력의 최대 오버슈트 M_p를 정상상태 응답 y_ss로 나눈 백분률
* y_p : 출력의 시간응답 최댓값
* 최댓값 시간 t_p : y_p될때 시간

지연시간 t_d delayed time
- 정상상태응답 y_ss의 50%에 도달하는데 소요되는 시간
상승시간 t_r rising time
- 과대감쇠 시스템(zeta >1) : 정상상태응답 y_ss의 10~90% 상승하는 시간
- 과소감쇠 시스템(0<zeta<1) : 정상상태응답 y_ss의 0~100% 상승하는 시간
정착 시간 t_s settling time
- 출력의 크기가 정상상테 응답의 y_ss의 (delta)%이내로 정착하는데 소요되는 시간
- 일반적으로 사용되는 (delta)값은 2

단순 1차 시스템의 전달함수

시정수(Time constant) T
- 감쇠 정도를 나타내는 지수함수가 e^-1=0.368이 되는 시간 -> y(t)=0.632에 얼마나 빨리도달하는지
- 시정수가 짧을수록 빨리 최종값(정상상태 응답)에 도달

단순 2차 시스템의 전달함수
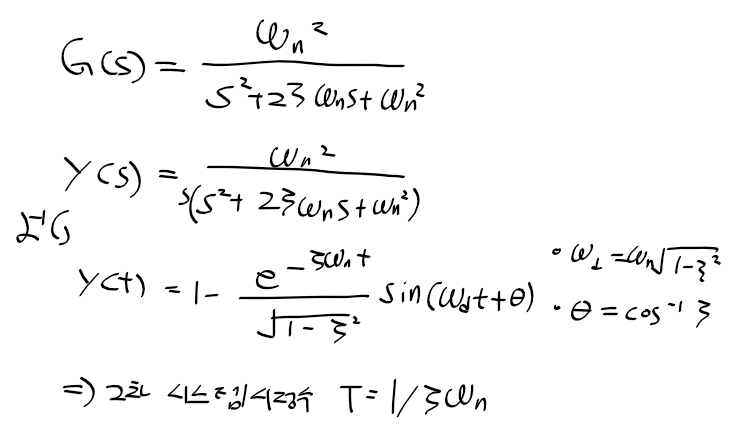
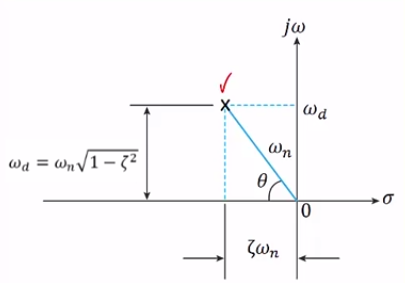

제어 시스템의 응답 성능
- 제어 시스템의 응답 성능은 과도 응답뿐만이 아니라 정상상태응답 성능도 동시에 만족해야함
- 정상상태 응답 성능은 입력 및 시스템 형태에 따라 판정함
* 시간이 지났을때도 정상상태 오차가 0으로 가는지 or 최소한으로 줄어드는지

단위 스텝 입력에 대한 폐루프 제어 시스템의 정상상태 오차
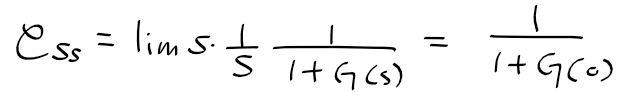
폐루프 제어 시스템의 정상상태 오차 크기
- 개루프 전달함수 G(s)의 형태에 따라 결정
- G(s)를 아래와 같이 정의할때 어떻게 G(0)의 변화를 봄

제 0형 시스템(N=0)의 정상상태 오차
- k_p는 G(s)의 분자 성분

n>=1 일때 스탭 입력에 대한 정상상태 오차
- e_ss = 0
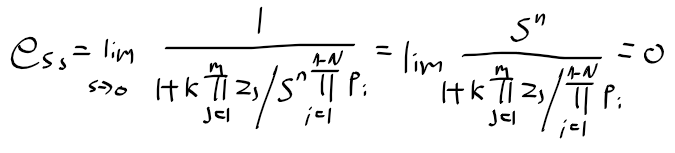
DC 모터 제어시스템의 스텝 기준 및 외란 입력에 대한 시스템 형태와 정상상태 응답 특성
1) 비례 피드백 제어 시스템

2) 단위 피드백 제어 시스템

비례 피드백 제어 시스템의 폐루프 전달함수 T(s)와 오차 e(s)

단위 스텝 기준 입력 r(s)에 대한 정상상태 오차
- 비례 피드백(k != 1) 제어 시스템(제 0형 시스템) -> 정상상태 오차 발생
- 단위 피드벡 제어 시스템(제1형시스템) -> 정상상태오차 = 0
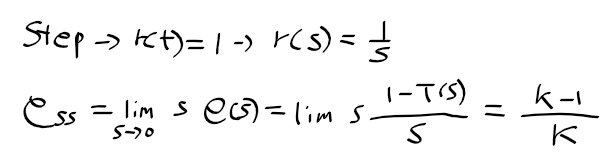
단위 스텝 외란 입력에 따른 정상상태 응답
- 단위 피드백 제어 시스템의 스텝 외란-출력 전달함수
=> 외란의 영향을 완전히 제거할수 없음
* 단위 스텝 외란에 대해 제 0형 시스템

'로봇 > 제어' 카테고리의 다른 글
| 제어공학 2 - 11 비선형 모델의 선형화 (0) | 2020.05.09 |
|---|---|
| 제어공학 2 - 10 제어성능 및 안정도 평가 (0) | 2020.05.09 |
| 제어공학 2 - 7 두 강체의 동적 시스템 (0) | 2020.05.09 |
| 제어공학 2 - 6 상태공간 (0) | 2020.05.08 |
| 제어공학 2 - 5 전달함수 (0) | 2020.05.08 |