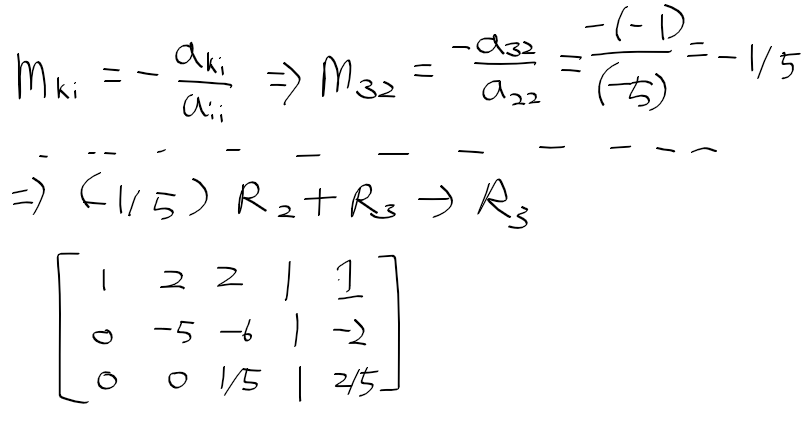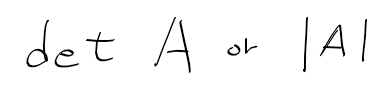집밖은 위험해

계급 rank

- 행렬 A가 주어질때, 1차 독립인 행 벡터의 최대 갯수를 계급이라 부름. rank A로 표기

* 행 벡터가 3개가 있더라도 1차 독립인 행 벡터가 2개 뿐이면 계급은 2가 됨.

동차 선형 시스템 homogeneous linear system

- 입력 벡터 B가 0인 선형 시스템으로 자명해 trivial solution은 모두 0이 됨.

역행렬 inverse matrix

- 정사각 행렬 A, B가 주어질때 A B = I를 만족하는 행렬 B는 A의 역행렬

역행렬의 존재 여부에 따른 분류

- 정착 행렬 regular matrix, 가역행렬 invertible matrix : 역행렬이 존재하는 행렬

- 특이 행렬 singular maxtrix : 역행렬이 존재하지 않는 행렬

행렬식 determinant

- 행렬의 판별식

- 2 x 2 행렬식

- 3 x 3 행렬식

부분행렬 submatrix

- 성분 a_ij의 행과 열을 제외한 행렬

여인수 cofactor

-해당 행렬의 성분에 대한 부분 행렬의 행렬식

수반 행렬 adjoint matrix

- 행렬 A의 역행렬을 구할때 사용되는 행렬

수반 행렬로 역행렬 구하기

크래머의 공식 cramer's formula

- 선형 시스템 AX = B가 주어질떄 k번쨰 성분의 해를 구하는 법

가우스 소거법 gauss elimination method

- 선형 시스템의 해를 구하는 방법 중 하나

- 행이나 열을 서로 교환하거나 기본 행연산을 쉽게 정리하도록 선형 시스템 AX = B에서 행렬 A와 열 벡터 B결합하여 아래의 첨가 행렬 augmented matrix을 만듬 

- 첨가 행렬을 사다리형 행렬 echelon form로 변환 후 아래에서 위로 역대입 backward subsitution하여 미지수를 구함

사다리형 echelon form만들기

1. 행렬 A의 a_11을 기준으로 a_i1(2 <= i <= n)을 0으로 만듦

2. a_22를 기준으로 a_i2(3<=i<=n)을 0으로 만듦

3. 위 과정을 반복하여 행렬 A의 주대각성분 아래 모든 요소들을 0으로 만듬

- 다음 행의 성분들을 0으로 만들기 위해 각 행들은 다음 연산을 수행(예제 보면서 이해 필요)

4. 사다리형 결과

역대입 backward subsitution

- 사다리형의 마지막 행인 n행에서 x_n을 구하고

- 이를 순차적으로 역대입하여 나머지 미지수를 구할 수있음

가우스 소거법을 이용현 선형 시스템의 해를 구하기

1. 선형 시스템 행렬로 정리하기

- 다음의 선형 시스템이 주어질 때

- 행렬로 정리하면 아래와 같다

2. 사다리꼴 만들기

- 이를 사다리꼴 형태로 정리하기 위해 첨가 행렬을 구하면 다음과 같다.

- 2번째, 3번쨰 행의 첫번째 요소를 0으로 만들기 위해, a_11을 기준으로 m_ki를 구하면

- 다음의 연산을 수행하면 2, 3번쨰 행의 첫번쨰 요소들이 0이 된다.

- 3번째 행의 2번째 요소도 0으로 만들어주어야 하므로 m_32를 구하고 연산을 수행하자

3. 역대입 수행하기

- 역대입을 통해 마지막 행 x_3을 다음과 같이 구할수 있음

4. 선형 시스템의 해 정리

- 선형 시스템에서 가우스 소거법으로 구한 해는 다음과 같다.

가우스 조던 소거법

- 가우스 소거법에서 계수 행렬 A를 위삼각 행렬로 만들고, 임의의수 한개만 존재하는 마지막 행에서 역대입으로 모든 해를 구함

- 첨가 행렬을 대각 또는 단위 행렬로 만들면, 각 행이 한개의 임의의 수만 가짐 -> 역대입 불필요

=> 가우스-조던 소거법

* 계수 행렬 A를 단위 또는 대각 행렬로 만드는데 연산이 더 많이 필요함

행렬식 determinant

- 정사각행렬 A에 대한 식으로 행렬에 대한 판별식

- 아래와 같이 표기

행렬식과 다양한 행렬들

- 행렬 A가 주어질때

- 특이행렬 singular matrix : detA = 0일때, A는 특이 행렬

- 일반 행렬 regular matrix : detA != 0 일때, A는 일반 행렬

행렬식 계산 방법

1. 여인수법

2. 삼각형법

이 있으나 생략

선형 시스템의 중요성

- 많은 자연, 공학 분야의 문제가 선형 시스템으 표현함

 -> 선형 시스템의 해를 구하는것이 매우 종요함.

- 현상을 미분 방정식으로 나타내도 해석적으로 해를 못구하는 경우 수치적으로 구해야 함.

차분 방정식 difference equation

- 수치적으로 구하는 경우 미분 방정식을 작게 나눈 구간으로 얻는 차분 방정식을 품

- 차분 방정식은 대규모 선형 시스템으로 이루어 짐

선형 시스템의 해를 구하는 방법

1. 직접 법 direct method

- 가우스 소거법, 역행렬, 크래머 공식

2. 반복법 iterative method

- 수치적 방법에서 많이 사용

선형 방정식 linear equation

- 상수 a, b, c, d가 주어지고 변수 x, y, z에 대한 아래와 같은 식을 선형 방정식이라 함

- 일반화하여 선형 방정식을 정리하자면 다음과 같다.

선형 시스템 linear system

- 여러개의 선형방정식으로 이루어 진 형태를 선형 시스템(1차 연립방정식)이라고 부름.

- 미지수 n개인 m개의 선형 방정식으로 이루어진 선형 시스템은 아래와 같음.

선형 시스템의 행렬 표현

- 행렬 A : m x n 형태의 계수 행렬 coefficient matrix

- 벡터 X : n x 1의 해 벡터 solution vector

- 벡터 B = m x 1의 입력 벡터 input vector

선형 시스템의 관련 용어

- 동차 선형 시스템 homogeneous linear system : 입력 벡터 B의 성분들이 모두 0인 경우의 선형 시스템

- 비동차 선형 시스템 nonhomogeneous linear system : 동차 선형 시스템이 아닌 선형 시스템

- 과잉결정 over determined : 식의 개수 m이 계수의 갯수 n보다 많은 경우

- 결정 determined : 식과 계수의 갯수가 같은 경우

- 과소 결정 under determined : 식이 계수보다 수가 적은 경우

- 일치 consistent : 해를 적어도 한개라도가지는 경우

- 불일치 inconsistent : 해가 전혀 없는 경우

행렬

- 숫자를 직사각형 형태로 나열

- 선형계 해석, 고유값 문제, 최적화, 컴퓨터 그래픽 등 다양한 분야에서 응용

미분 방정식 경계값 문제에서의 행렬

- 수치적으로 풀면 결과가 행렬로 연립방정식의 해를 구하는 문제가 됨

행렬 matrix

- 직사각형 형태의 숫자들의 배열

정사각행렬 square matrix

- 행과 열의 길이가 같은 행렬

- 주대각성분 principal diagonal component : 정사각행렬의 대각선 위의 성분

영행렬

- 행렬의 모든 성분이 0인 행렬

사상 mapping 및 변환 transformation

- 벡터 공간 X, Y에서 X에속하는 벡터 x가 Y에 속하는 벡터 y에 대해 y = F(x)로 대응 correspondence하는 것

1차 변환 linear transform

- 선형성을 만족하는 변환

확률 행렬 stochastic matrix

- 모든 성분이 음의 값이 아니고, 각 행 요소들의 합이 1인 정사각행렬

마르코브 과정 markov process

- 현재 상태에 대한 확률이 이전 상태에 의존하는 확률 과정

전치 행렬 transpose matrix

- 행과 열을 바꾸어 얻는 행렬

삼각행렬 triangular matrix

대각행렬 diagonal matrix

- 주대각 성분을 제외하고 나머지 요소들이 0인 행렬

스칼라 행렬 scalar matrix

- 주대각성분이 모두 같은 대각 행렬

단위 행렬 unit matrix

- 주대각성분이 1인 스칼라행렬

벡터 공간의 개요

- 벡터를 2차원, 3차원에서 제한할 것이 아니라 n차원 까지 확장하여 다룰수 있음

- 이런 확장된 차원의 벡터를 벡터 공간 집합의 원소로서 다룸

벡터 공간 vector space

- 집합 V가 덧셈과 스칼라곱이 정의되는 원소 집합일때, 10가지 공리를 만족하는 집합 V를 벡터 공간

- 벡터 공간 V의 원소를 벡터

* 자세한 공리는 생략

- 스칼라를 실수로 제한하면 -> 실 벡터 공간 real vector space

- 복소수 까지 다룬다면 -> 복소 벡터 공간 complex vector space

벡터 공간의 예시

1. 실수 집합 R

2. n차원 실벡터의 집합 R^n

3. n차 이하 다항식 집합 P_n

4. 모든 실수에 정의되는 실 함수 f 집합

등

부분 공간 subspace

- 벡터 공간 V의 부분집합 W가 V에서 정의되는 덧셈과 스칼라곱을 따르는경우

 => 부분집합 W는 벡터 공간 V의 부분 공간

1차 결합 linear combination

- 아래와 같이 스칼라에 대해 벡터가 주어지면 1차 결합

1차 독립 linear independent 및 1차 종속 linear dependent

- 아래의 벡터와 스칼라의 1차 결합이 c1 = c2 = ... = c0에서만 성립되면 벡터들은 1차 독립

- 아닌 경우에 성립되면 1차 종속

기저 basis

- 벡터 공간 V의 모든 벡터가 1차 독립인 벡터 x1, x2, ..., xn의 1차 결합으로 표현가능한 경우

 -> x1, ... , xn을 벡터 공간 V의 기저

차원 dimension

- 기저를 이루는 벡터의 갯수를 벡터공간 V의 차원 -> dimV 로 표기

생성공간 span

- 주어진 벡터의 모든 1차 결합 집합

벡터의 곱

- 내적 inner proudct와 외적 outer product

내적이란?

- 두 벡터의 곱으로 차원이 하나 감소하여 내적이라 부름.

- 점 연산이라 dot product 혹은 결과가 스칼라 값이라 scalar product라고도 부름

사영벡터란?

- 두 벡터 a와 b가 주어질때, b를 a의 벡터 선상에 사영하여 얻는 a방향의 벡터

 => a에 대한 b의 사영벡터 projection vector of b onto a

- 내적의 정의에 따라 b의 a방향 성분을 구하면

- 사영 벡터의 크기

- 단위 벡터를 이용한 사영 벡터 표현

외적 outer product

- 외적에 의해 하나의 차원이 증가하여 외적이라고 부름.

- 두 벡터 a, b의 외적을 a x b로 표기하므로 cross product

- 혹은 외적의 결과가 벡터이기 때문에 vector product

외적 계산

-  다음과 같이 벡터 성분이 주어질때 외적 계산 

자연에서의 물리량

- 스칼라 scalar : 크기만 가지는 양. ex : 길이, 거리, 속력, 일

- 벡터 vector : 크기와 방향을 갖는 양. ex : 위치, 변위, 속도, 힘

위치

- 변위 displacement : 위치의 변화

- 위치 벡터 position vector : 해당 위치를 향하는 물리량

벡터

- 시작점 O와 끝점 A을 가짐

- 벡터의 성분 : 시작점을 원점으로 하여 끝점의 좌표축에 대한 요소

- 평면 벡터의 성분

- 벡터의 크기 norm, magnitude

단위 벡터 unit vector

- 크기가 1인 벡터. 벡터 a와 같은 방향을 갖는 단위 벡터 u는 아래와 같음

방향 단위 벡터 directional unit vector

- 각 좌표축에 평행한 단위 벡터

- 3차원 직교좌표계상 x, y, z방향에 대한 방향단위벡터를 i, j, k로 정의

- 각 방향 단위벡터의 요소는 i = [1, 0, 0], j = [0, 1, 0], k = [0, 0, 1]

- 임의의 벡터 a = [a1, a2, a3]은 다음과 같이 방향 단위 벡터로 표현 가능

초기값 문제

- 미분방정식, 초기조건으로 구성

초기값 문제에 사용하는 다양한 수치적 해법

1. 오일러 방법 euler method

2. 테일러 방법 talyor method

3. 룽게-쿠타 방법 runge-kutta method

주어진 1계 초기값

오일러 방법

- x >= x0 일때, y(x)의 해를 구하기 위해 x의 구간을 h로 나누면

- 단순 오일러 방법 : x0에 대해서 y의 도함수를 구하고 일반화 시켜 해를 구하는 방법

테일러 방법

- 2항 테일러 방법 : y(x)의 테일러 급수에 x = x_{n+1}을 대입하여 아래의 식을 구하고, 앞의 두 항만 골라 구한 식

3. 룽게-쿠타 방법 runge-kutta 방법

- 테일러 방법에서 등간격 h를 사용하였고, f(x, y)를 계속 미분하였음.

- 룽게-쿠타 방법은 테일러 방법과 유사하나 f(x,y)에 따라 h를 적절히 바꾸고, f(x, y)를 여러번 미분할 필요가 없음

- 방법은 생략

문제를 해결하는 방법

1. 해석적 방법 anlaytic method

- 수학적 정의와 정리들을 이용하여 문제를 푸는 방법

2. 수치적 방법 numerical method

- 컴퓨터 연산을 통해 문제를 해결하는 방법

f(x) = 0을 만족하는 근 x를 찾기 위한 해석적 방법과 수치적 방법

1. 해석적 방법

- 1차 방정식 linear equation과 2차 방정식 quadratic equation만 구할 수 있음

2. 수치적 방법 - 이분법 bisection method

- 이분법 : 구간을 반복적으로 이분하여, 오차 범위 내의 근을 구하는 방법

- 아래의 함수 f(x) =0를 만족하는 근 x를 찾는다면

- f(x) = 0 해를 찾기 위한 이분법 의사 코드

해석적 방법과 수치적 방법의 특징

1. 해석적 방법

- 해를 구할수 있는 경우 true solution을 얻을 수 있다.

- 해를 찾을수 없거나 계산량이 너무 많을 수 있음.

2. 수치적 방법

- 컴퓨터로 풀수 있도록 문제를 수정해야함

- 근사해를 구함

- 대부분 문제에서 해를 얻을 수 있음

수치 해석 관련 용어

- 참해 true solution : 실제 정확한 해

- 근사해 approximate solution : 실제 해에 가깝도록 근사하여 구한 해.

- 절단오차 truncation error : 근사에 의해서 해에서 나타나는 오차

- 자리수 오차 roundoff error : 컴퓨터의 소수 표현에 의해 생기는 오차

- 전파 오차 propagation error : 반복 중 이전 오차가 다음으로 넘어가는 정도

무한등비급수 infinite geometric series

- 첫 항이 a, 공비가 r인 무한 급수

조화급수 harmonic series

- 다음의 무한급수를 조화급수라 부름

- 조화급수는 발산하는 대표적인 급수

교대급수 alternating series

교대 조화 급수 alternating harmonic series

거듭 제곱 급수 infinite power series

- 급수의 중심 x_0(center)에 거급제곱들의 합인 급수

테일러 급수 Taylor series

- 우선 거듭 제곱 함수의 도함수들을 구해보자

- 거듭 제곱 함수와 도함수들에 x = x_0를 대입하면 다음과 같이 정리할 수 있다.

- 이를 계수 a_m에 대해서 정리하면 다음과 같다.

테일러 급수 Taylor series

- 위 계수 a_m으로 거듭 제곱 급수를 정리하면 아래의 식 f(x)가 테일러 급수이다.

매클로린 급수 McLaurin series

- 테일러 급수의 x_0에 0을 대입하여 얻을 수 있는 급수

매클로린 금수의 예시

- 지수함수, 삼각함수, 로그 함수, 등비급수, 이항급수 등

오일러 공식