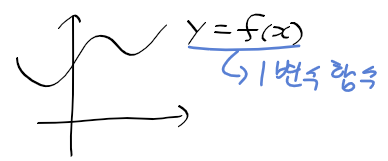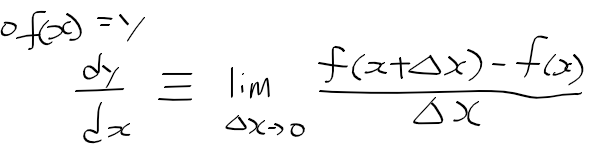집밖은 위험해

벡터 확률 변수, 벡터 랜덤 변수 vector random variable

- 확률 변수가 2개 이상인 경우 -> 벡터 랜덤 변수 or 벡터 확률 변수라 함

- 기존의 1변수 확률 변수를 길이가 2이상인 열 벡터로 정의

* 그냥 다변수 확률 변수라 하겠다.

결합 확률 밀도 함수 joint pdf

- 다변수 확률 분포를 따르는 확률

 * 결합 확률이란? 여러개의 확률 변수들이 결합된 경우의 확률

- 아래의 그림은 변수가 2개인 결합 확률 밀도 함수로 평면에 대한 확률을 보여줌

- 이변수 표준 정규 분포의 경우 확률 밀도 함수를 3차원 플로팅 시킨 결과

- 1변수 확률 밀도 함수는 아래와 같이 직선에 대한 확률로 나타낸다.

결합 누적 분포 함수 joint cdf

- 다변수 확률 분포를 따르는 누적 확률

- 확률 변수 X, Y가 주어질때 결합 누적 확률 분포 함수 F는 아래와 같음.

다변수 확률 변수(랜덤 벡터 확률변수)의 통계적 특징

- 일변수 확률변수(스칼라 확률변수)와 동일하게 정의

공분산 행렬

- 다변수 확률 변수에서 확류변수들간에 퍼진(영향)의 정도

- 다음의 공분산 행렬이 주어질때, 2변수 확률분포 표본 데이터들의 분포

- 위 공분산 행렬의 고유치와 고유벡터

확률 변수 random variable

- 실행 결과들을 수치로 대응시키는 함수

 * 확률 변수는 변수 variable이 아니라 하나의 실수 함수(real function)

확률 변수의 예시

- 두개의 동전을 동시에 던지는 실험

 => 확률변수 X에 사용가능한 x = {0, 1, 2}

확률 분포

- 확률 변수 개별 값들의 분포

- P(X = x)로 정리하면 확률분포표를얻을수 있음.

=> 확률 함수 : 개별적인 확률 값들을 확률 공간상의 확률로 정리하는 함수

확률 함수의 종류

- 이산 확률 분포 : 확률 변수가 이산 확률변수인 경우. => 확률 질량 함수 PMF Probability Mass Function

- 연속 확률 분포 : 확률 변수가 연속 확률변수인 경우 => 확률 밀도 함수 PDF Probabilty Density Function

- 누적 분포 함수 CDF cumulative Distribution Function

  : 확률 질량/밀도 함수를 누적하여 얻은 확률변수

 => 아래는 정규분포의 누적 분포 함수

확률밀도함수와 확률 질량함수

- 확률 밀도함수 : 연속확률변수 X의 누적확률분포 F(X)의 미분으로 정의

- 확률 질량함수 : 이산확률변수 X의 누적확률분포 F(X)의 미분으로 정의

기대값 Expectation

- 학률변수의 평균

- 표본 성질 : 일반 데이터들의 성질

- 확률 분포의 성질 : 모집단(or 모델)의 성질 

 * 기호구분 : 일반 데이터(샘플, 표본)와 모집단(전체 집단)의 평균과 표준 편차 기호를 아래와 같이 구분함

표본 기댓값 expectation of sample 과 모집단 기댓값 expectation of population

- 샘플 데이터들의 평균은 아래의 식으로 계산.

- n_x를 x의 횟수라 한다면, 아래와 같이 정리되고 n이 커지면 통계적 확률(근사 확률 ) p(x)를 얻음

 => n이 전체 공간의 갯수만큼 된다면 모집단의 평균을 구하게 됨.

표본에 대한 분산으로 모집단 분산 구하기

- 표본에 대한 분산 식이 주어지면 아래의 정리를 통해 n이 최대가 되면 모집단의 분산이 됨.

통계적 현상 statistical phenomena

- 여러번 관찰해서 법칙을 찾아낼수 있는 현상

확률 실험

- 반복 할수록 규칙성이 존재하는 행위

확률

- 특정 현상이 확실히 발생할 정도

확률 법칙

- 임의의 실험에서 사건에 확률을 배정하는 규칙

수학적 확률

- 표본 공간 S과 S를 구성하는 사건 A가 있을때, 다음의 P(A)를 수학적 확률

 * 수학적 확률은 각 사건들이 일어날 가능성이 모두 동일하다고 가정

 * 동전 2개를 던질때 앞면이 0개, 1개, 2개가 나올 확률을 다 동일하게 1/3, 1/3, 1/3이라고 가정하면 안됨.

통계적 확률

- 동일한 현상이 일어날지 불확실한 경우, 여러번 실험해서 얻은 사건에 대한 확률은 상대적인 횟수로 추정

- 상대적인 횟수 relative frequency는 n번 실험할때 r회 일어난 경우 r/n.

 * 동전 2개를 던질때 앞면이 0개, 1개, 2개가 나올 (통계적) 확률은 1/4, 1/2, 1/4

수학적 확률과 통계적 확률의 차이

- 수학적 확률은 표본 공간을 구성하는 사건들이 동일한 확률을 가지고 있다고 생각

- 통계적 확률은 여러번 반복했을때 나온 정도(상대적 횟수)로 확률을 추정

통계적 확률 정리

- n회 실험 할때, A의 상대 횟수 r/n이 특정한 수 p에 수렴하는 경우 => 통계적 확률

- 정확한 p 값은 알수 없으나, n이 충분히 크다면 근사적으로 상대 도수를 통계적 확률로 본다.

표본 공간 sample space과 확률 공간 probability space

- 표본 공간 : 관측으로 얻은 결과 집합

- 사건 : 표본 공간의 부분 집합

- 확률 공간 : 표본 공간을 확률에 대응시킨 결과 집합

주변 확률과 조건부 확률

- 주변 확률 marginal probability : 두 사건 A, B가 존재할때, A나 B 한 가지의 사건만 일어날 확률

- 조건부 확률 conditional probability : 두 사건 A, B가 발생 했는데, B의 확률을 알때 A가 일어날 확률

전체 확률 이론 total probability thorem

- 사건 A들의 합집합이 표본 공간이고, 서로 배타적일때 사건 B는 다음의 그림과 같이 구성됨.

- 사건 B의 확률은 B와 사건 A들의 교집합들의 합

귀납적 추론과 연역적 추론

- 통계학은 대부분의 경우 표본에서 모집단을 추정

 => 귀납적 추론 inductive inference : 개발적 사건으로 일반적 법칙 유도

- 연역적 추론 deductive inference : 일반적 법칙으로 개별적인 사건 유도

베이즈 정리 bayes thorem

- 일반적인 법칙을 알수 없는 불확실한 상황에서 의사 결정 문제를 다룰때 중요하게 사용됨

- (연역적 추론 방식인) 확률로 (일반적인 법칙을 유도하는) 귀납적 추론 방식을 행하는 행위

베이즈 정리와 확률의 의미

- 기존의 확률 : 직접 확률 direct probability

- 베이즈 정리 : 역확률 inverse probability

베이즈 법칙(정리?)로 정리하기

- 표본 공간 S와 분할 영역 A들이 주어질때, B가 난 경우 A_i에서 일어날 확률이 얼마나 될까?

- 조건부 확률 conditional probability 을 전체 확률 정리 total probability thorem으로 정리하면

 => 사건 B가 발생했을때 A_i가 일어날 확률을 알고 싶으나 모르는 경우

    사건 A_i가 일어났을때 B가 일어날 확률을 안다면 구할수 있다.

* 개별적 사건에 대한 확률로 일반적인 법칙을 추론해냈다?

통계적 패턴인식에서의 베이즈 정리

- 특징 벡터 x가 관측되었을때 클래스 omega_i를 찾자. P(omega_j | x) = ?

 => p(x | omega_i)를 알면 구할수 있다. (클래스가 주어질때, 특징 벡터 관측에 대한 조건부 확률)

- 베이즈 정리 : 우도를 알때 사후 확률을 구하는 정리

베이즈 정리 용어 정리

- 사전 확률 priori probability : P(omega_1). 클래스 omega_1의 확률

- 정규화 상수 : p(x), x 확률 결정에 영향을 주지않는 정규화 상수

- p(omega_1 교집합 x ) = 1/10 (임의로 정의)

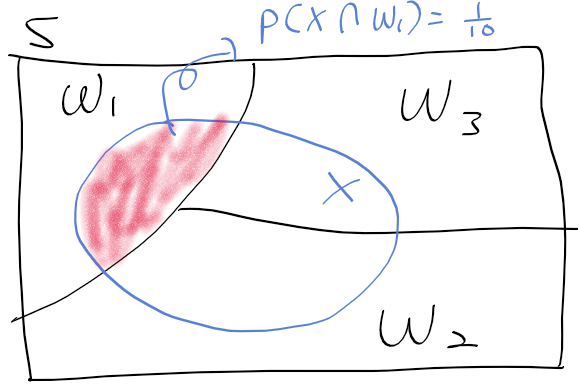
- 우도 likelihood : 클래스 omega_i가 주어질때, 관측 x이 일어날 확률

- 사후 확률 posterior probaility : 관측 x이 있을때, 클래스 omega_1에 속할 확률

 => 특징 벡터 x가 관측되었을때, 분류한 결과가 omega_1일 확률은 0.3

 => 특징 벡터 x는 30%의 확률로 omega_1로 분류된다!!

회귀분석 regression analysis

- 변수들간의 관계를 정리하여 모델링하는 통계 기법

 => 자연 과학, 사회과학에서 널리사용됨

- 수학적 모델을 가정하고, 실제 데이터로 모델을 추정하는 방법. 예측에 주로 사용

=> 표본을 잘 나타내는 적합한 근사 함수를 구할 수 있음

 * 근사 함수 : 회귀 직선, 회귀 곡선

선형 회귀 linear regression

- 회귀 직선 : 데이터를 가장 잘 수학적으로 모델링 하는 선

- 선형 회귀는 샘플 데이터를 통해 이를 가장 잘 표현하는 회귀 직선을 구하는 과정

선형 회귀 모델의 종류

최소 자승법 Method of Least Mean Square 

- 샘플 데이터와 임의의 직선의 제곱 오차를 최소로하는 직선을 구하는 방법

1. 아래의 직선을 가정

2. 데이터가 하나가 아니라 두개인 이변량인 경우 측정값은 아래와 같이 정리하자

 * 단변량 : 하나인경우 univariate,  이변량 bivariate : 두개인 경우,    다변량 multivariate : 여러개인 경우

3. 각 x의 값에 대한 y의 값들을 정리하면 아래와 같다.

4. 측정값 y_i와 위 직선과의 평균 제곱 오차 MSE Mean Squared Error는

5. MSE가 최소가 되는 alpha와 beta가 구하면 회귀 직선이 됨.

6. MSE를 alpha와 beta에 대해 편미분 하고, 0과 같다고 가정하여 각 변수에 대해 정리하면

회귀 곡선 regression curve(다항식 회귀? polynomial regression)

- 회귀 직선과 달리 1차식이 아니라 2차식으로 나타낸 회귀식

1. 아래와 같이 회귀 곡선 모델을 정의

2. 이에 대한 계수 a, b, c는 평균 제곱 오차를 최소화하도록 아래와 같이 정리할수 있음

- 아래는 회귀 곡선을 구하는 다항식 회귀 예시

통계 용어들

- 데이터 분석 과정 data analysis process : 데이터를 처리하여 정보 도출하는 과정 -> 요약, 추정 단계 수행

  => 아래의 그림은 데이터 분석 과정

- 요약 : 정보 손실을 줄이면서 정리

- 추론(추정) inference : 요약된 데이터로 특정 집단에 대한 사실을 추론해내는것

- 모집단 population : 데이터 분석 대상 전체

- 표본 sample : 수집된 모집단 데이터의 일부분

- 표본 분포 sampling distribution : 샘플들로 부터 얻은 통계적인 분포

데이터 분석의 성질

- 타당성 validity : 의도대로 수집하였는지

- 신뢰성 reliability : 항상 동일한 결과가 나오는지

통계학 매개변수(파라미터)들

- 파라미터 parameter : 모집단 population을 표현하기 위한 모수(고정된 값)

  => 추론 inference를 통해 파라미터를 구할수 있게 된다.

- 평균 mean : 데이터 총합을 데이터 갯수로 나눈 값 -> 데이터 분포의 무게 중심

- 분산 variance : 데이터들이 퍼진 정도. (데이터 - 평균) 제곱 합 / 데이터 갯수

- 표준 편차 standard deviation : 분산은 제곱 합을 통해 구하므로 데이터 단위가 달라짐.

                                      기존의 데이터 단위와 맞추기 위해 제곱근 수행

- 바이어스(편향) bias : 데이터가 특정 위치에 집중(편향)된 정도

- 공분산 covariance : 샘플 데이터가 단변수가 아니라 다변수 인경우 각 변화량에 대한 변화하는 정도.]

- 상관 계수 correlation : 서로 다른 두 변수 X, Y 간에 상관관계의 정도.

                            => 하나의 변수가 변함에 따라 다른 변수에 얼마나 영향을 미치는가

- 왜도 skewness : 분포가 치우쳐진(asymmetry) 정도. 

- 첨도 kurtosis : 통계 분포가 뽀족한 정도

확률 변수 random variable

- 사건 X

확률 probaility

- 사건 X1이 일어날 확률

=> P(X= x1)

기대값 expectation

- 확률 변수 X가 주어질떄 X에 대한 평균

- E(X)로 표기

분산 variation

- 모든 [(각 확률변수 - 해당 확률변수의 기대값)의 제곱]의 합/경우의 수

=> 평균에서 멀어진 정도

표준 편차 standard varaition

- 분산의 제곱근 

확률 분포 probability distribution

- 확률들의 분포 형태

- 이산 확률 분포와 연속 확률 분포로 분류

이산 균일 분포 discrete uniform distribution

- 모든 공간에 균일한 분포

- 1/경우의 수

이항분포 binomial distribution

- 일정 확률 p를 독립 시행 n번 할때 확률 분포

다항 분포 multinomial distribution

- 이항 분포를 일반화 한것

- 이항분포에서 결과가 참 거짓 2가지 뿐인것과는 달리 k개가 존재

연속 균일 분포 continuous unitform distribution

- 이산 균일분포와 동일하나 연속공간에서 정의

정규 분포 normal distribution

- 종 형태의 확률 분포로 많이 사용

이외 확률분포는 생략

- 역감마분포

- 포아송분포

- 지수분포

일반 통계학에서의 확률

- 주사위에서 1이 나올 확률이 1/6

베이즈 통계학에서의 확률

- 약속 시간에 늦을 확률 1/2

 => 개인적인 믿음 정도(주관주의 확률)를 확률로 정의하는 통계학

베이즈 통계학

- 주관주의 확률을 다루는 통계학

일반 통계학과 베이즈 통계학에서의 차이

1. 일반 통계학

 - 모집단에서 n개의 샘플을 추출

 - 표본 집단으로 기대값 x1을 구함.

 - 다른 표본 집단으로 기대값 xn을 구하고 반복함.

 - 전체 기대값(x1 + ... + xn)/반복 횟수 T

   => 추정값을 구할 수 있음.

2. 베이즈 통계학

- 가설을 세움

- 모집단에서 표본을 추출하여 

- 베이즈 정리

  => 추정값과 그 추정값에 대한 주관적인 확률을 구함.

자연 과학에서 유용하게 사용되는 도함수

- 기울기 벡터, 발산, 회전

기울기 벡터 gradient

- 스칼라 함수 f가 주어질때 grad f가 기울기 벡터

방향 도함수 directional derivative

- 스칼라 함수 f의 a 방향 변화율

- D_a f는 a 방향의 변화율로 theta 값에 따라 i방향과 j방향 성분을 구할수 있음.

 -> 방향도 함수는 편미분을 임의의 방향으로 나타낸 개념

기울기 벡터의 의미

- 스칼라 함수 f의 기울기 벡터는 다음의 방향을 가리킨다.

포텐셜 potential과 보존장 conservative field

- 아래의 식이 주어질때 스칼라 함수를 기울기 벡터의 포텐셜, 기울기 벡터를 보존장

등위 곡선과 법선 벡터

- 곡선 f(x, y) = c가 곡면 z = (x, y)의 등위 곡선일때, 곡면의 매개변수 벡터함수 r(t) = [x(t), y(t)]로 정의

- 곡선 f(x, y) =c 를 시간 t에 대해서 미분하면 다음과 같다.

=> 법선 벡터는 스칼라 함수 f가 가장 급격히 증가하는 기울기 벡터

스칼라 함수 scalar function

- 함수의 크기만을 구하는 함수

벡터 함수 vector function

- 크기와 방향을 동시에 가지는 함수

- 스칼라 값들을 요소로 가짐

벡터장 vector filed

- 벡터 함수의 크기와 방향을 함께 그린 그래프

ex. 속도장 velocity field, 힘장 force filed, 자기장 magnetic field

다변수 함수 개요

- 대부분의 현상과 공학 문제는 다변수 함수로 표현됨

1변수 함수 single variable funtion

- y = f(x)와 같이 하나의 독립 변수만을 가지는 함수

도함수(미분)

- 1변수 함수에서 함수 y의 x에 대한 변화율

다변수 함수 mutiple variable function

- f(x, y) = z와 같이 독립 변수가 2개 이상인 함수

등위 곡선 level curve

- 2변수 함수에 z = c 로 얻을수 있는 곡면

상미분 ordinary derivative

- 1변수 함수 y = f(x)의 도함수(미분)

편미분 partial derivative

- 다변수 함수에서 종속변수의 한개의 독립변수에 대한 변화율