가우스 소거법 gauss elimination method
- 선형 시스템의 해를 구하는 방법 중 하나
- 행이나 열을 서로 교환하거나 기본 행연산을 쉽게 정리하도록 선형 시스템 AX = B에서 행렬 A와 열 벡터 B결합하여 아래의 첨가 행렬 augmented matrix을 만듬

- 첨가 행렬을 사다리형 행렬 echelon form로 변환 후 아래에서 위로 역대입 backward subsitution하여 미지수를 구함
사다리형 echelon form만들기
1. 행렬 A의 a_11을 기준으로 a_i1(2 <= i <= n)을 0으로 만듦
2. a_22를 기준으로 a_i2(3<=i<=n)을 0으로 만듦
3. 위 과정을 반복하여 행렬 A의 주대각성분 아래 모든 요소들을 0으로 만듬
- 다음 행의 성분들을 0으로 만들기 위해 각 행들은 다음 연산을 수행(예제 보면서 이해 필요)

4. 사다리형 결과

역대입 backward subsitution
- 사다리형의 마지막 행인 n행에서 x_n을 구하고

- 이를 순차적으로 역대입하여 나머지 미지수를 구할 수있음

가우스 소거법을 이용현 선형 시스템의 해를 구하기
1. 선형 시스템 행렬로 정리하기
- 다음의 선형 시스템이 주어질 때

- 행렬로 정리하면 아래와 같다

2. 사다리꼴 만들기
- 이를 사다리꼴 형태로 정리하기 위해 첨가 행렬을 구하면 다음과 같다.

- 2번째, 3번쨰 행의 첫번째 요소를 0으로 만들기 위해, a_11을 기준으로 m_ki를 구하면

- 다음의 연산을 수행하면 2, 3번쨰 행의 첫번쨰 요소들이 0이 된다.

- 3번째 행의 2번째 요소도 0으로 만들어주어야 하므로 m_32를 구하고 연산을 수행하자
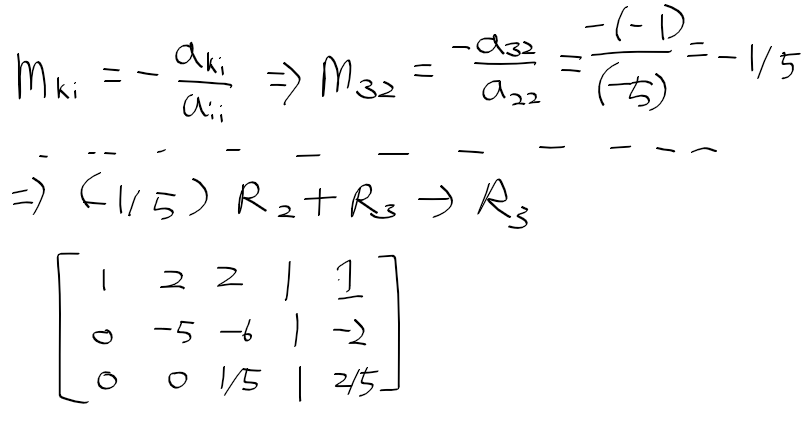
3. 역대입 수행하기
- 역대입을 통해 마지막 행 x_3을 다음과 같이 구할수 있음

4. 선형 시스템의 해 정리
- 선형 시스템에서 가우스 소거법으로 구한 해는 다음과 같다.

가우스 조던 소거법
- 가우스 소거법에서 계수 행렬 A를 위삼각 행렬로 만들고, 임의의수 한개만 존재하는 마지막 행에서 역대입으로 모든 해를 구함
- 첨가 행렬을 대각 또는 단위 행렬로 만들면, 각 행이 한개의 임의의 수만 가짐 -> 역대입 불필요
=> 가우스-조던 소거법
* 계수 행렬 A를 단위 또는 대각 행렬로 만드는데 연산이 더 많이 필요함

'수학 > 공업수학, 확률' 카테고리의 다른 글
| 공업수학 - 33. 다변수 함수와 편미분 (0) | 2020.07.15 |
|---|---|
| 공업수학 - 32. 계급과 역행렬, 행렬식, 크래머 공식 (0) | 2020.07.15 |
| 공업수학 - 30. 행렬식과 선형 시스템 (0) | 2020.07.14 |
| 공업수학 - 29. 행렬 (0) | 2020.07.14 |
| 공업수학 - 28. 벡터 공간 (0) | 2020.07.14 |