행렬식 determinant
- 정사각행렬 A에 대한 식으로 행렬에 대한 판별식
- 아래와 같이 표기
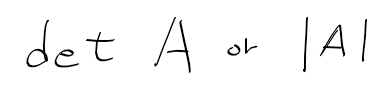
행렬식과 다양한 행렬들
- 행렬 A가 주어질때
- 특이행렬 singular matrix : detA = 0일때, A는 특이 행렬
- 일반 행렬 regular matrix : detA != 0 일때, A는 일반 행렬
행렬식 계산 방법
1. 여인수법
2. 삼각형법
이 있으나 생략
선형 시스템의 중요성
- 많은 자연, 공학 분야의 문제가 선형 시스템으 표현함
-> 선형 시스템의 해를 구하는것이 매우 종요함.
- 현상을 미분 방정식으로 나타내도 해석적으로 해를 못구하는 경우 수치적으로 구해야 함.
차분 방정식 difference equation
- 수치적으로 구하는 경우 미분 방정식을 작게 나눈 구간으로 얻는 차분 방정식을 품
- 차분 방정식은 대규모 선형 시스템으로 이루어 짐
선형 시스템의 해를 구하는 방법
1. 직접 법 direct method
- 가우스 소거법, 역행렬, 크래머 공식
2. 반복법 iterative method
- 수치적 방법에서 많이 사용
선형 방정식 linear equation
- 상수 a, b, c, d가 주어지고 변수 x, y, z에 대한 아래와 같은 식을 선형 방정식이라 함

- 일반화하여 선형 방정식을 정리하자면 다음과 같다.

선형 시스템 linear system
- 여러개의 선형방정식으로 이루어 진 형태를 선형 시스템(1차 연립방정식)이라고 부름.
- 미지수 n개인 m개의 선형 방정식으로 이루어진 선형 시스템은 아래와 같음.

선형 시스템의 행렬 표현
- 행렬 A : m x n 형태의 계수 행렬 coefficient matrix
- 벡터 X : n x 1의 해 벡터 solution vector
- 벡터 B = m x 1의 입력 벡터 input vector

선형 시스템의 관련 용어
- 동차 선형 시스템 homogeneous linear system : 입력 벡터 B의 성분들이 모두 0인 경우의 선형 시스템
- 비동차 선형 시스템 nonhomogeneous linear system : 동차 선형 시스템이 아닌 선형 시스템
- 과잉결정 over determined : 식의 개수 m이 계수의 갯수 n보다 많은 경우
- 결정 determined : 식과 계수의 갯수가 같은 경우
- 과소 결정 under determined : 식이 계수보다 수가 적은 경우
- 일치 consistent : 해를 적어도 한개라도가지는 경우
- 불일치 inconsistent : 해가 전혀 없는 경우
'수학 > 공업수학, 확률' 카테고리의 다른 글
| 공업수학 - 32. 계급과 역행렬, 행렬식, 크래머 공식 (0) | 2020.07.15 |
|---|---|
| 공업수학 - 31. 가우스 소거법 (0) | 2020.07.15 |
| 공업수학 - 29. 행렬 (0) | 2020.07.14 |
| 공업수학 - 28. 벡터 공간 (0) | 2020.07.14 |
| 공업수학 - 27. 내적과 외적 (0) | 2020.07.14 |