728x90
가우스 뉴턴 방법 개요
- 비선형 최소 자승법으로 근사 해를 구하기 위해 레벤버그-마퀴트 뉴턴 방법. 즉 LM 방법을 사용할 예정
- LM 방법은 가우스 뉴턴 방법을 기반으로 함
- 가우스 뉴턴 방법은 테일러 전개 2차식에서 시작
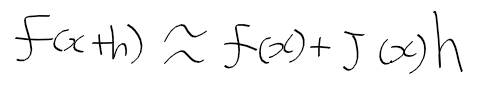
자코비안과 그라디언트, 헤시안
- 자코비안의 요소들은 함수 f의 미분들

- 함수 F의 그라디언트
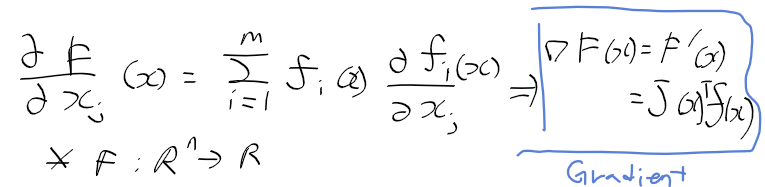
- 함수 F의 헤시안

가우스-뉴턴 방법
- 함수 f(x + h)를 l(h)로 근사화 하면

- F(x+h)에 대한 근사식은 아래와 같다.

- L(h)를 정리하면
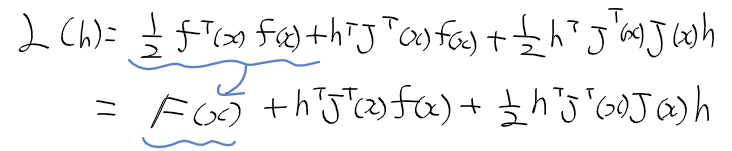
- L(h)가 최소가 되는 h를 구하기 위해

- 이 식을 정리하면 가우스 뉴턴 알고리즘을 정리 할 수 있다.

300x250
'수학 > 선형대수, 최적화' 카테고리의 다른 글
| 선형대수(복) - 1. 벡터론 (0) | 2020.08.02 |
|---|---|
| 최적화 - 18. LM 방법의 비선형 최소 자승방법 적용 (0) | 2020.07.26 |
| 최적화 - 16. 비선형 최소자승법 (0) | 2020.07.26 |
| 최적화 - 15. 비선형 최소자승법 개요 (0) | 2020.07.26 |
| 최적화 - 14. 쿼시 뉴턴 방법 (0) | 2020.07.26 |