집밖은 위험해

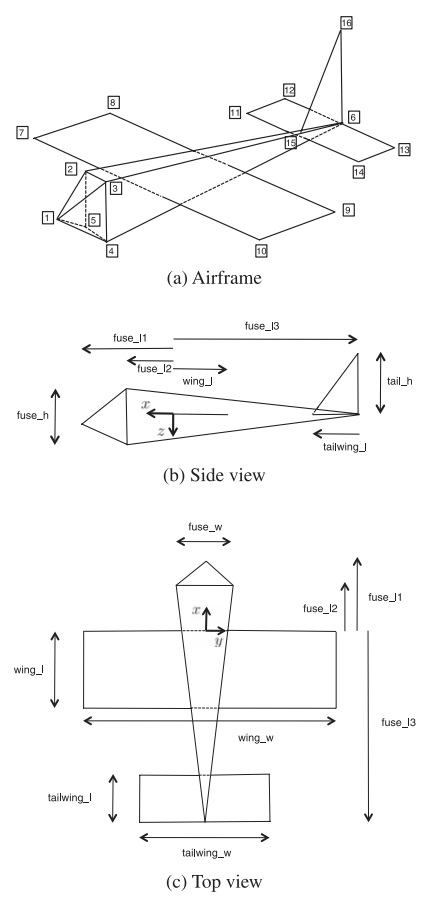
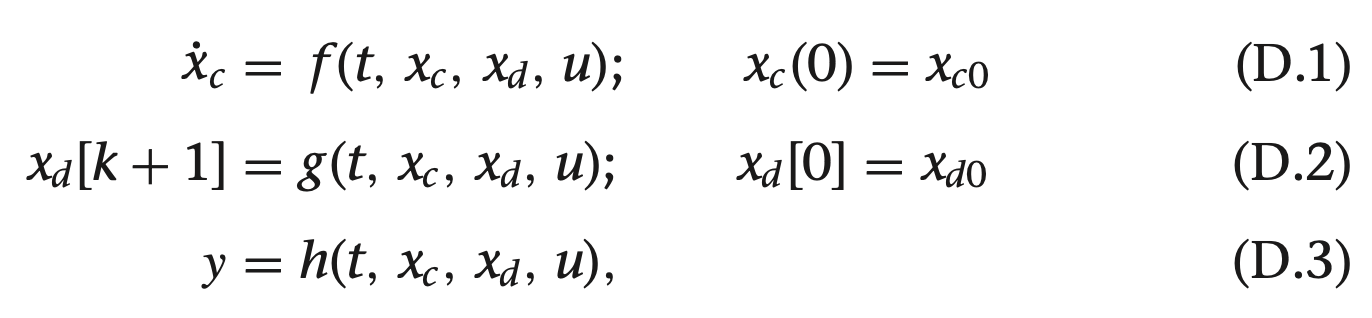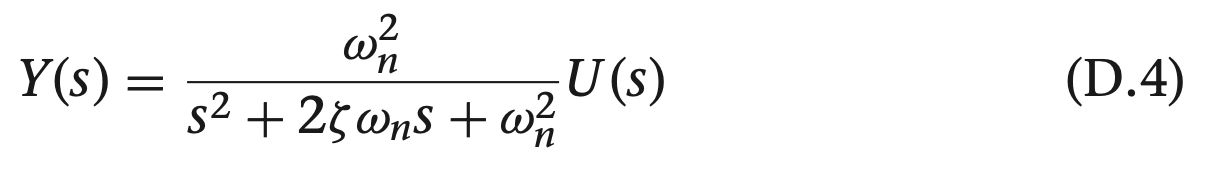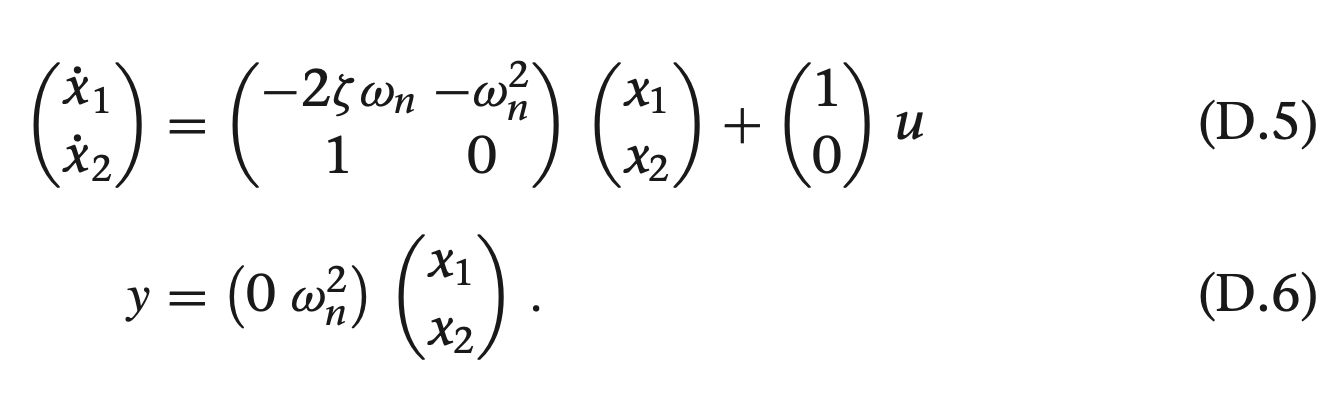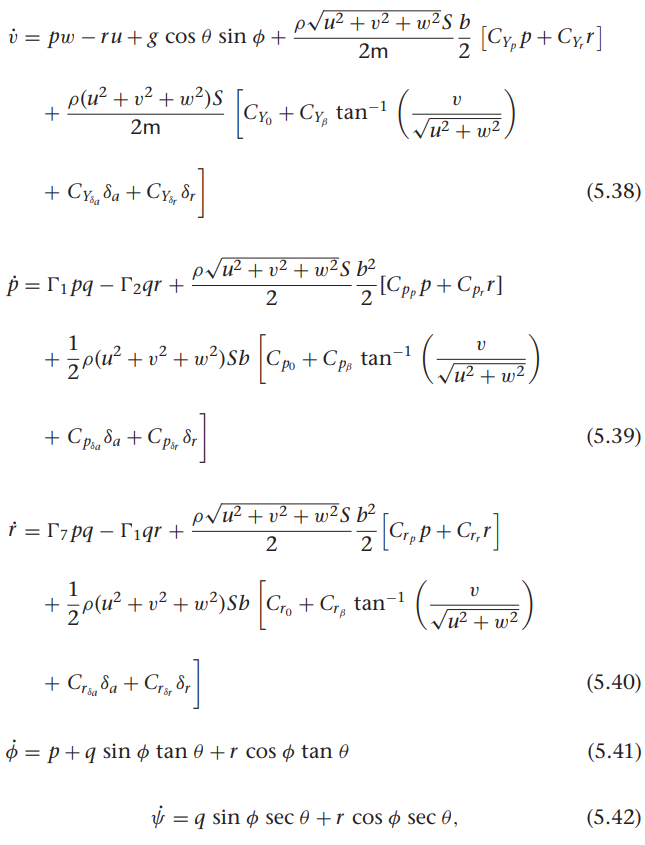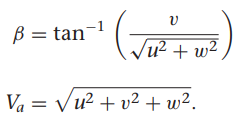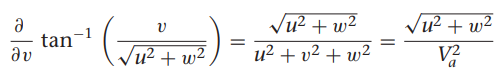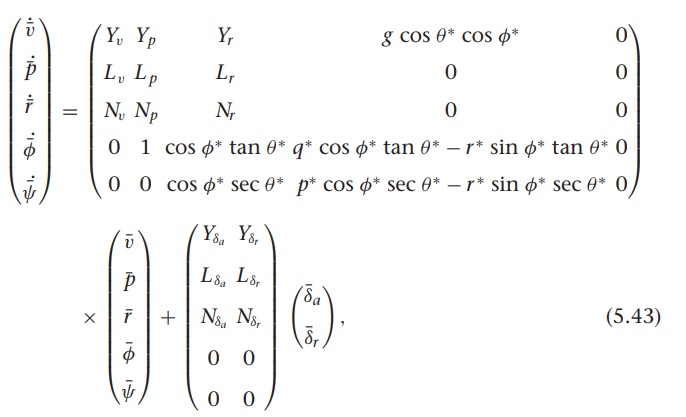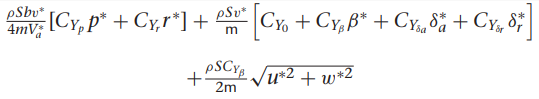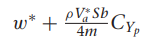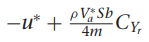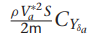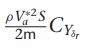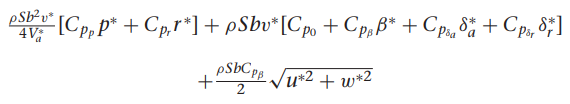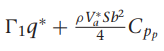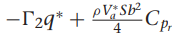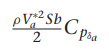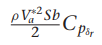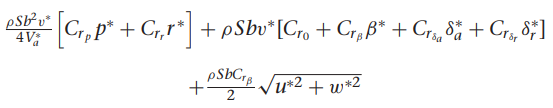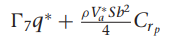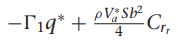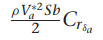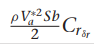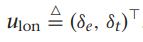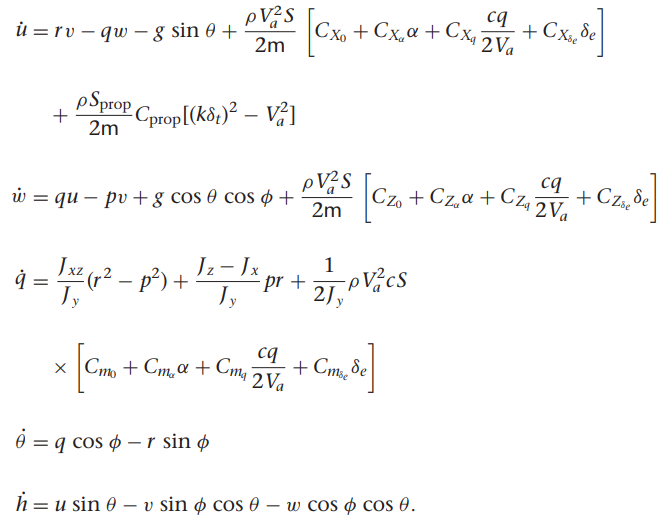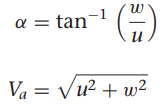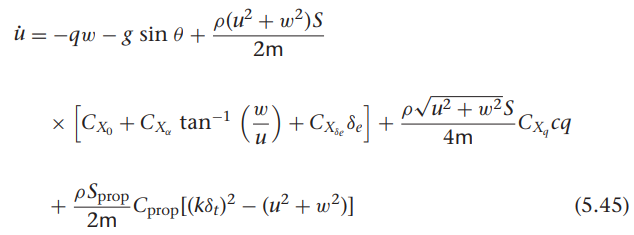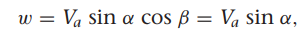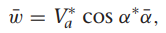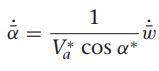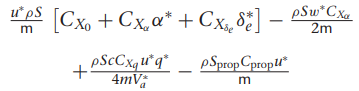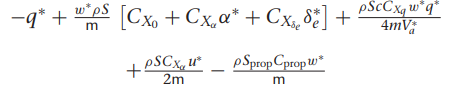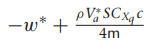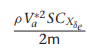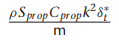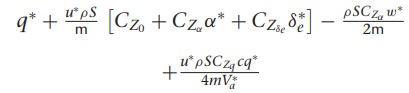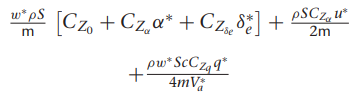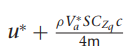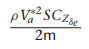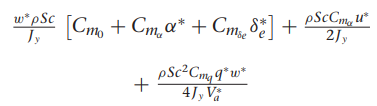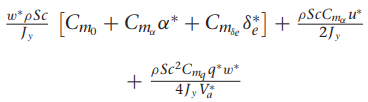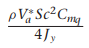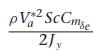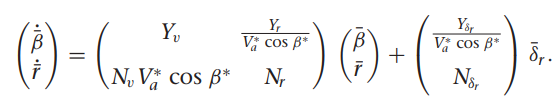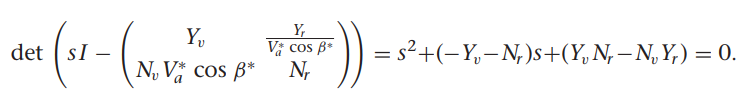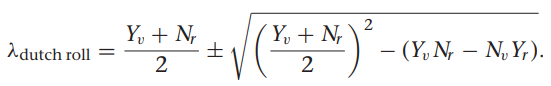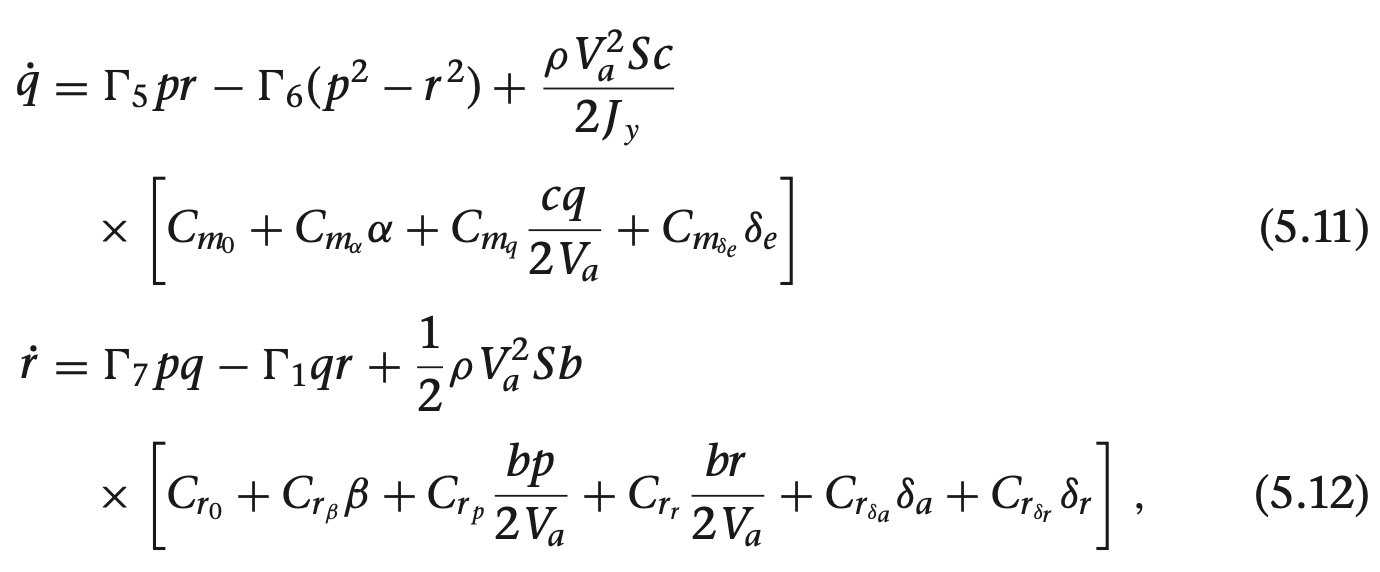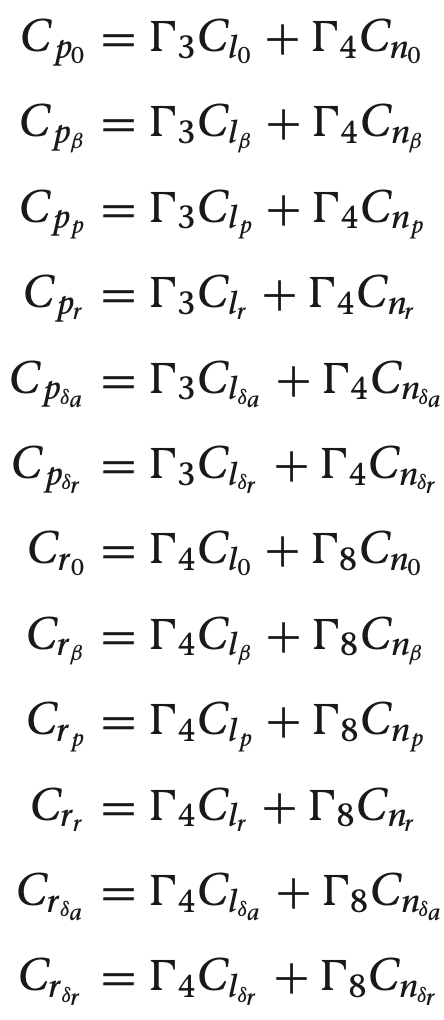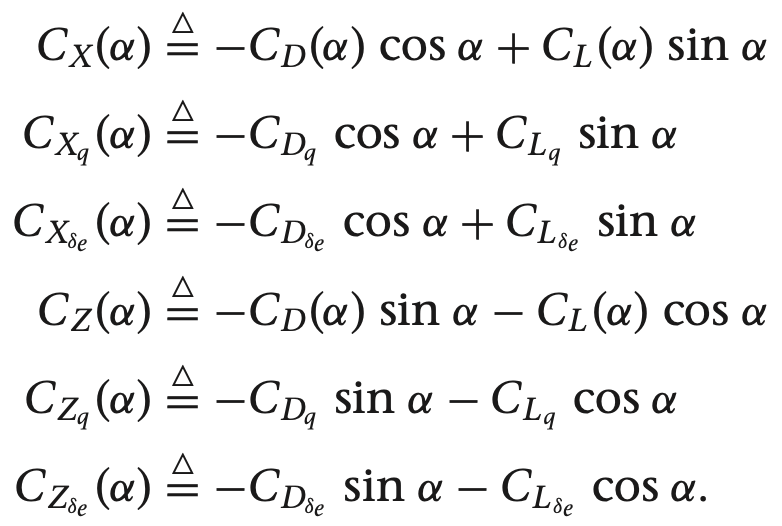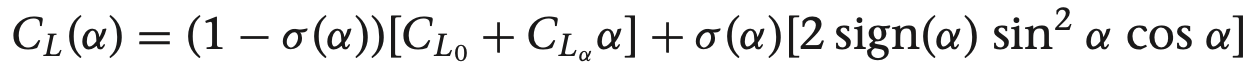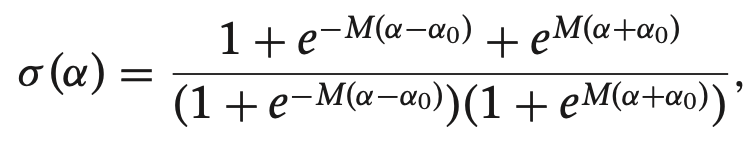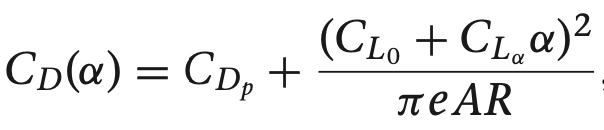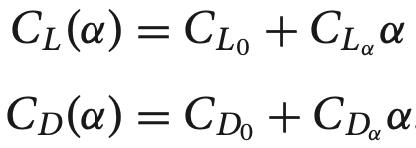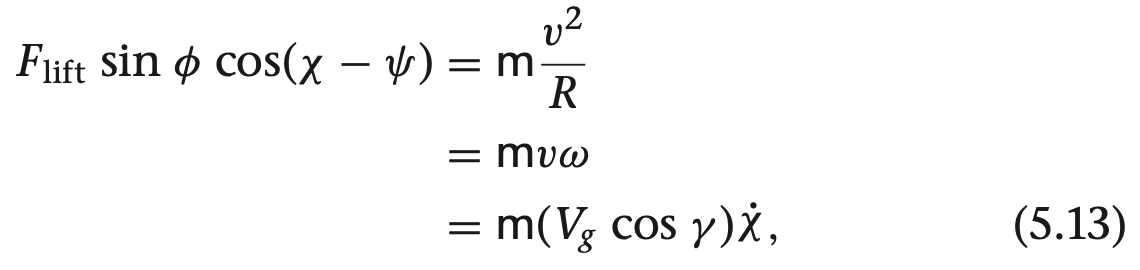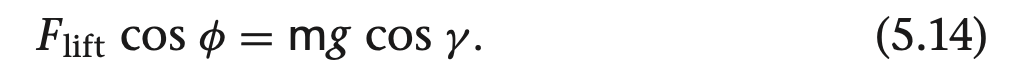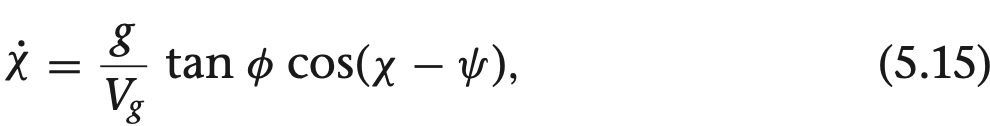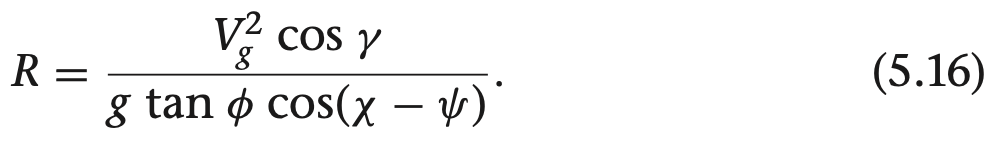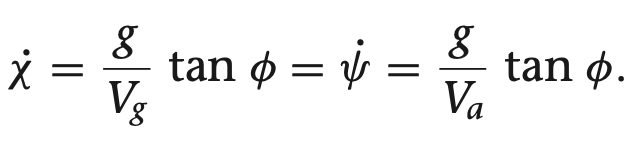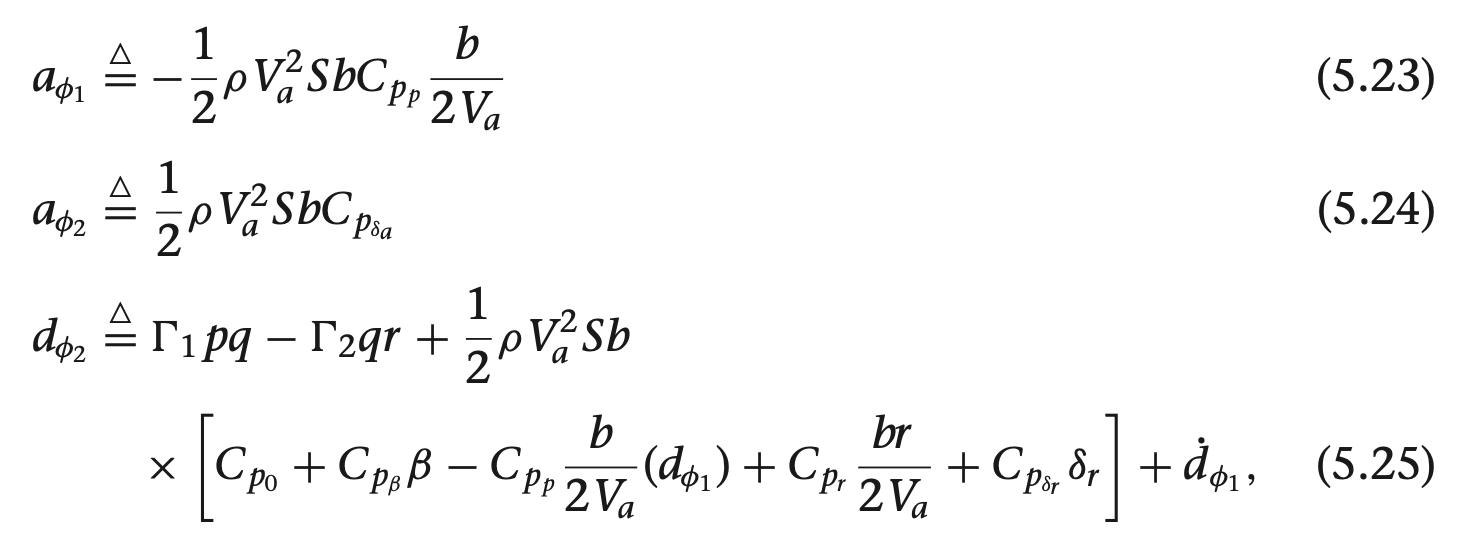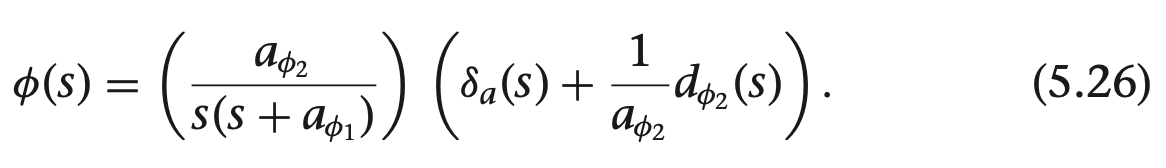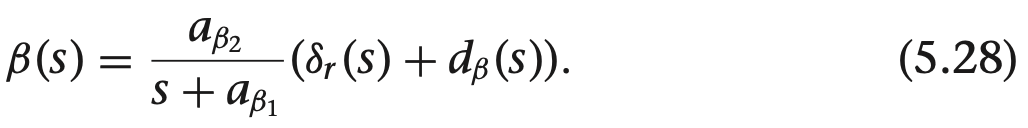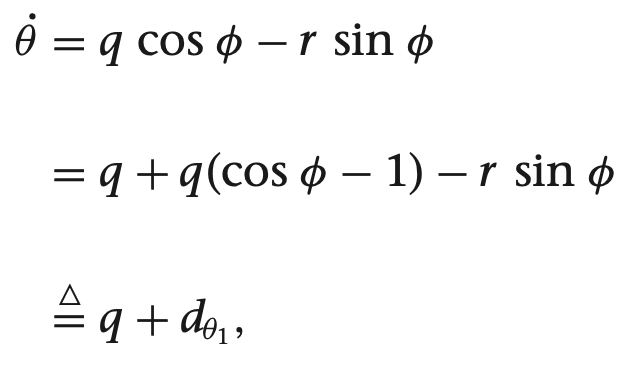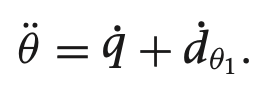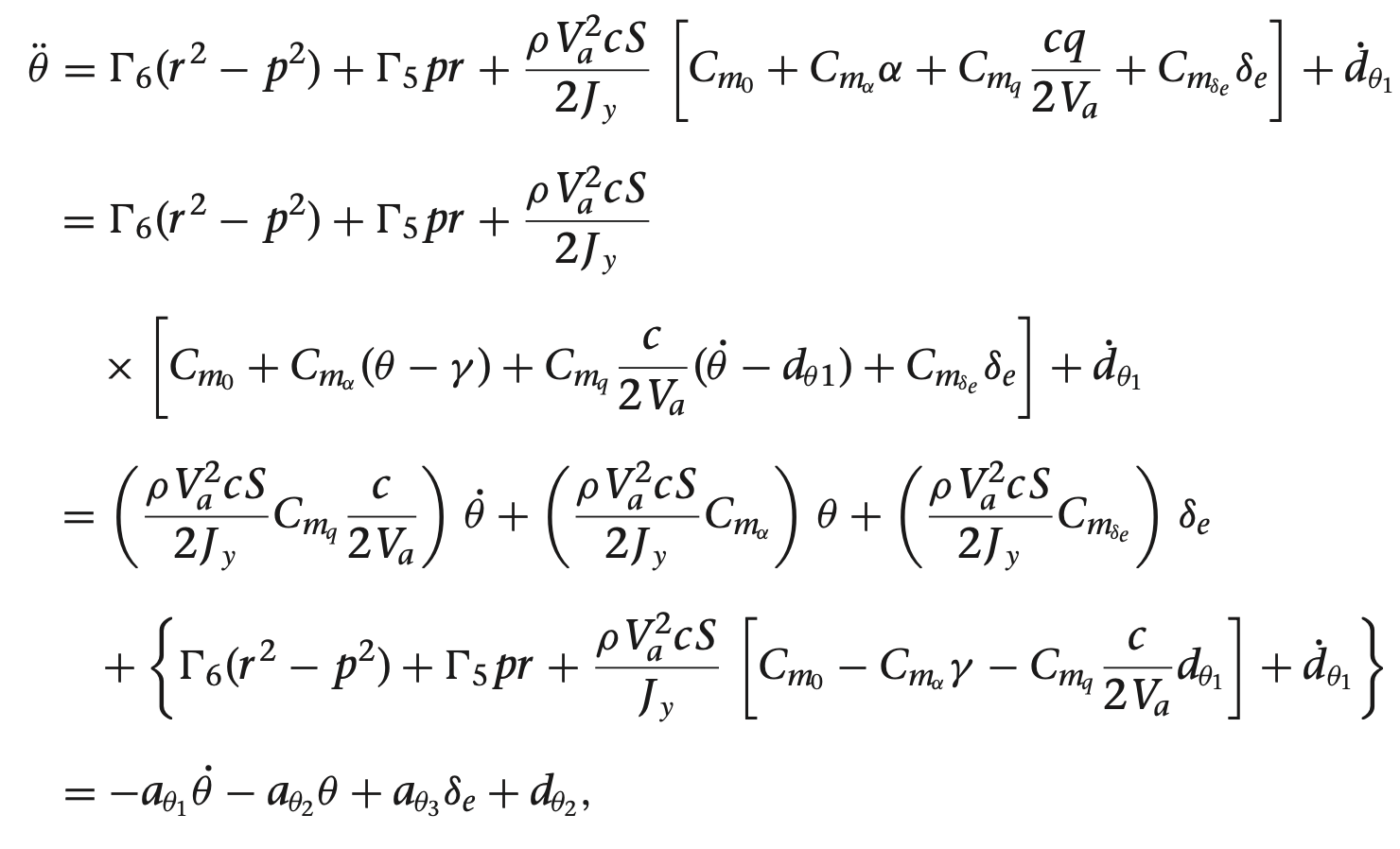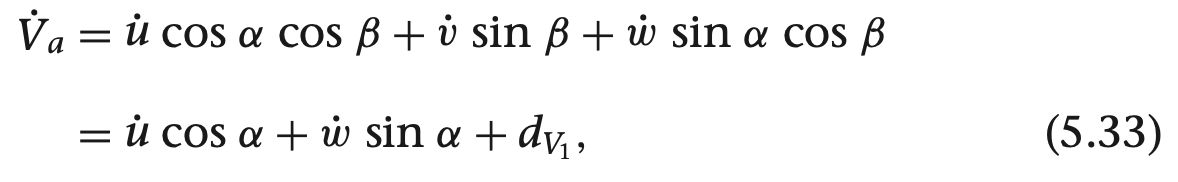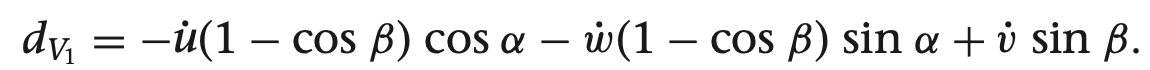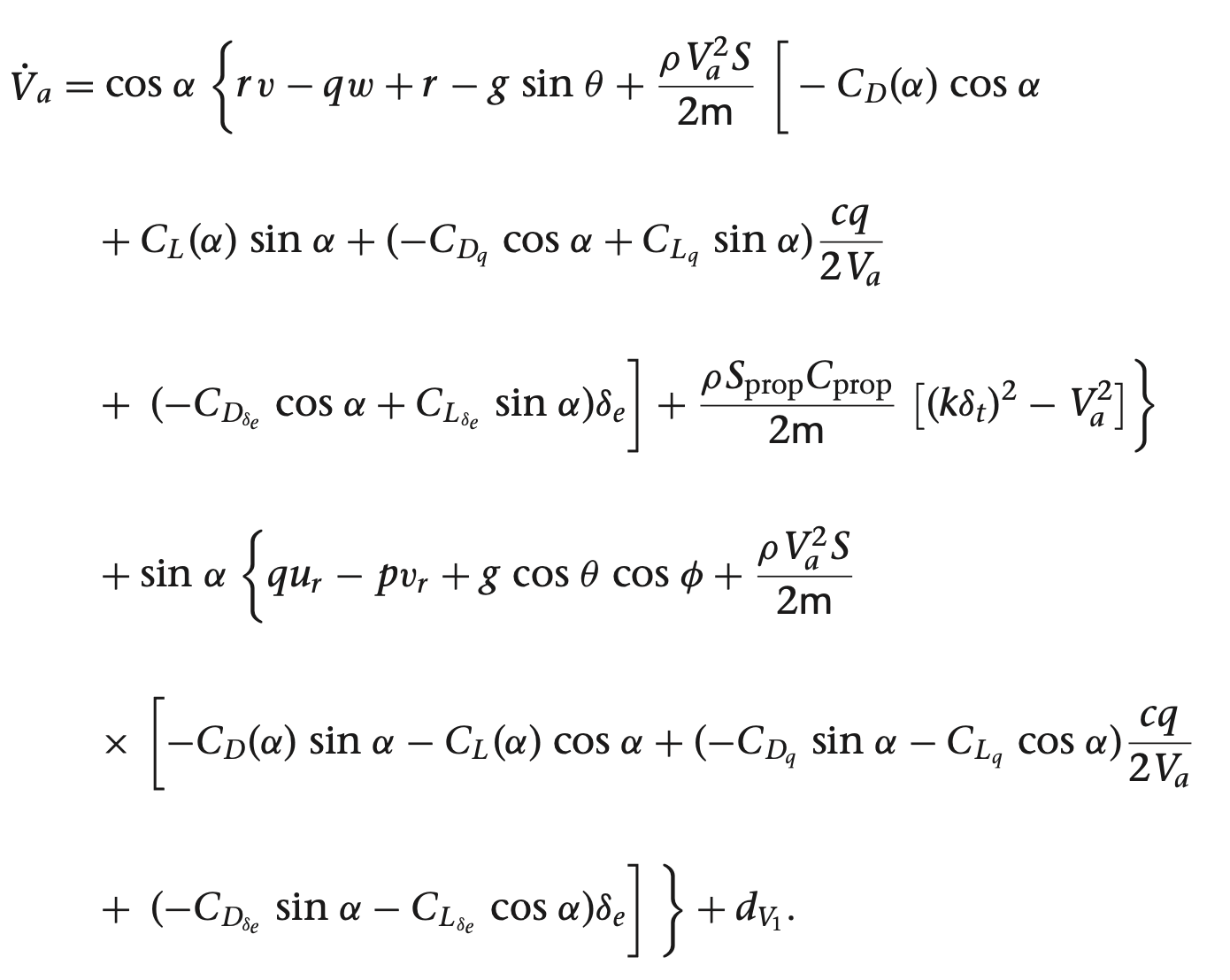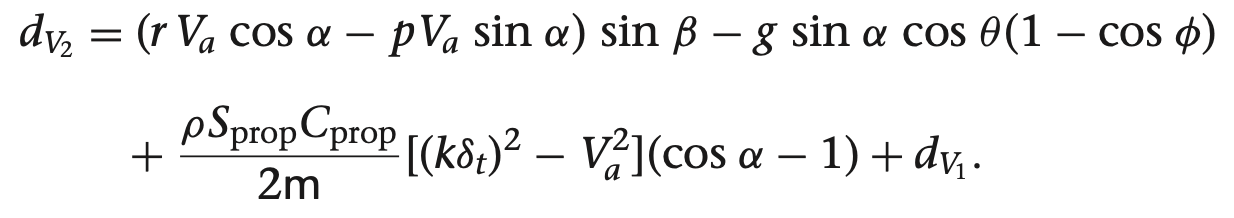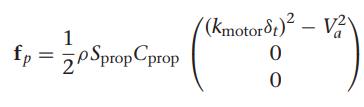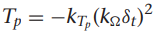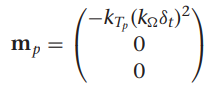1. s 펑션 정리하기

2. 템플릿 완성하기

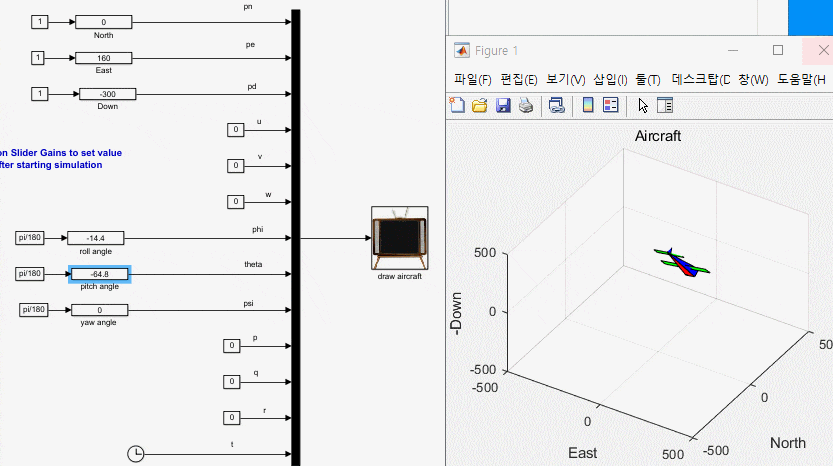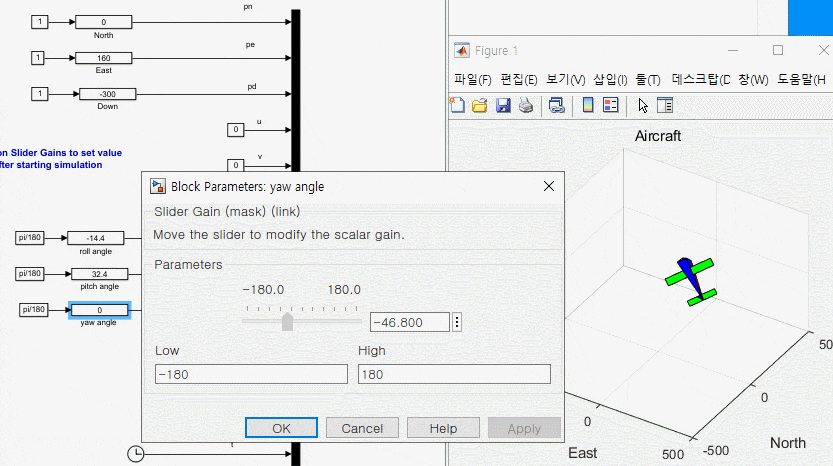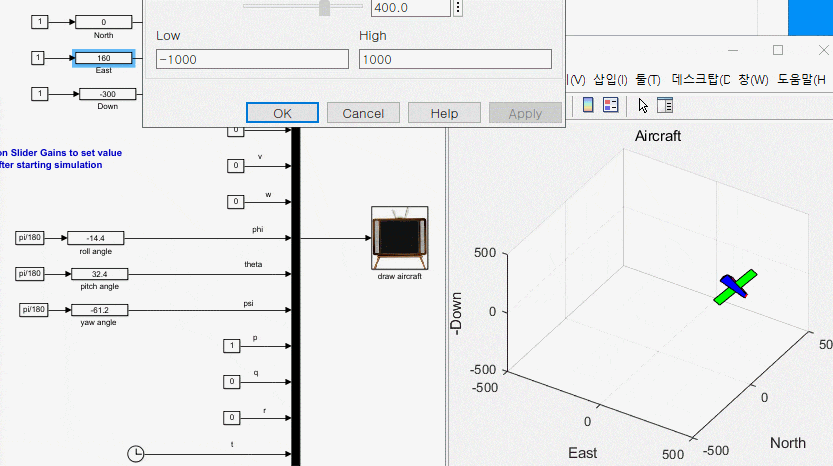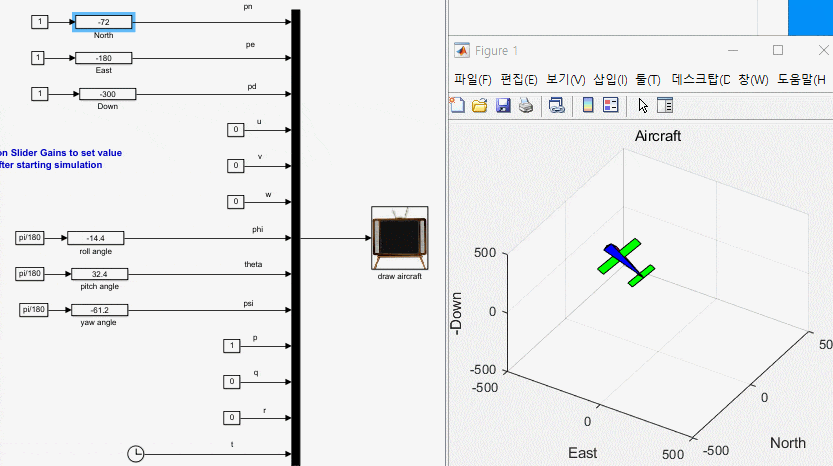
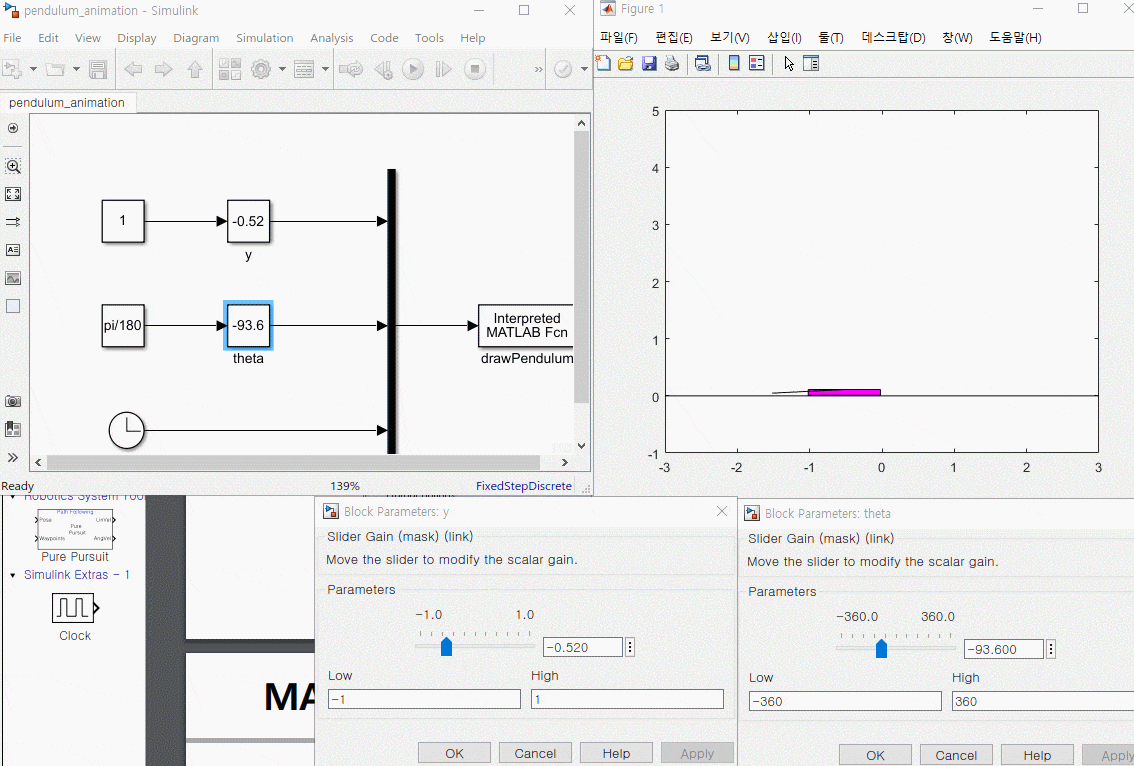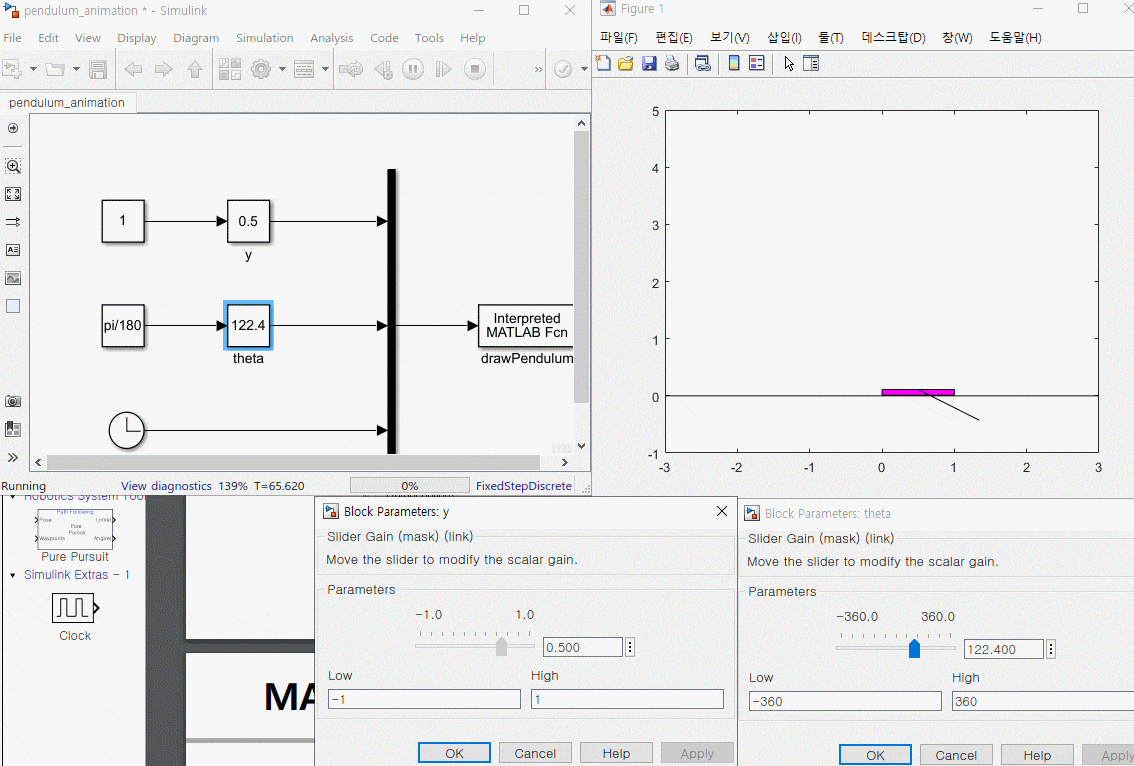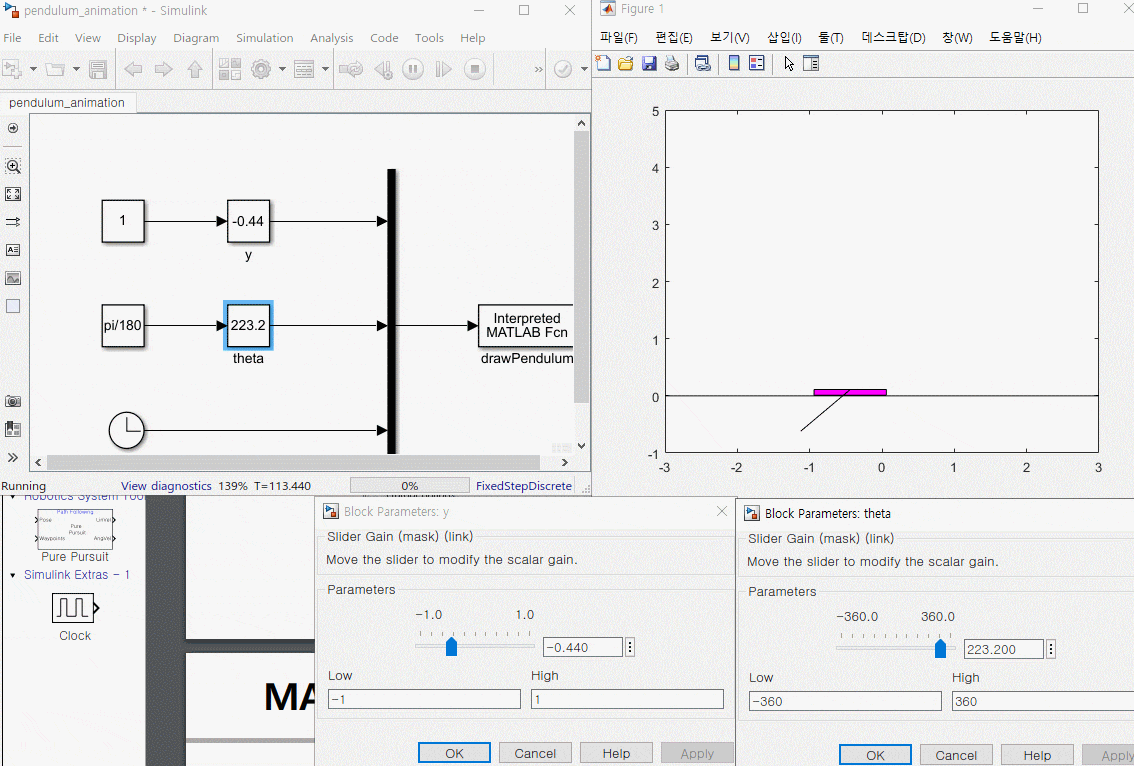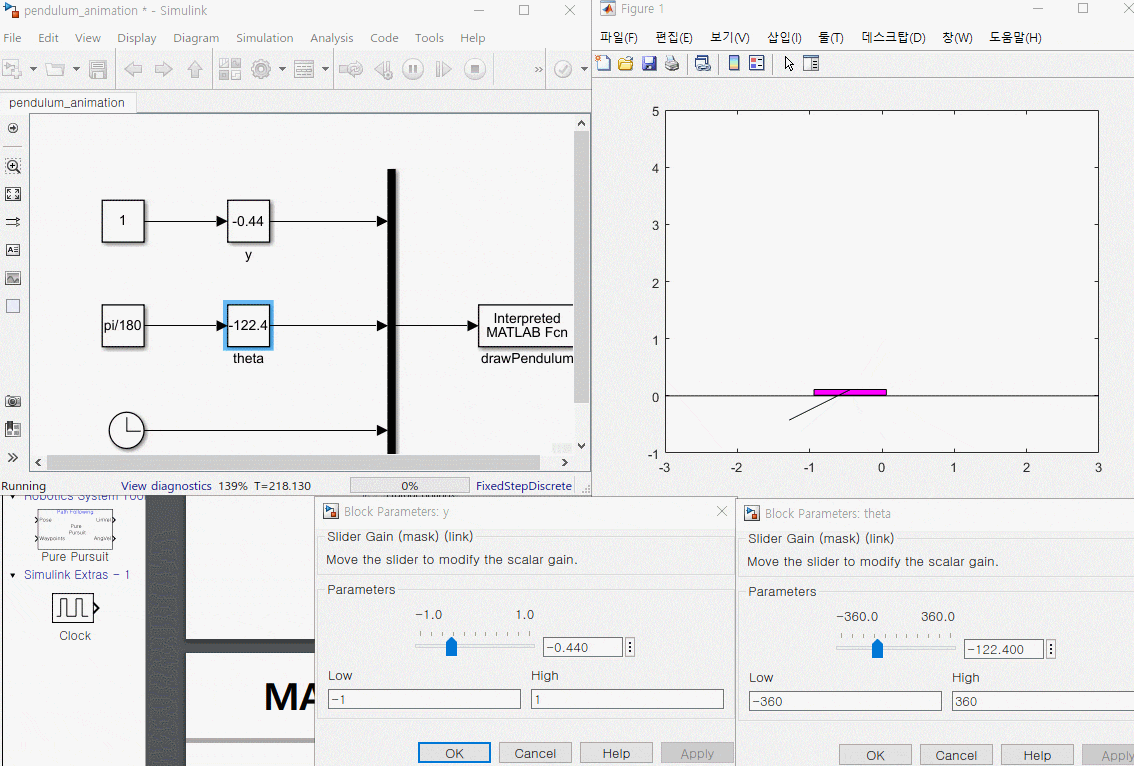
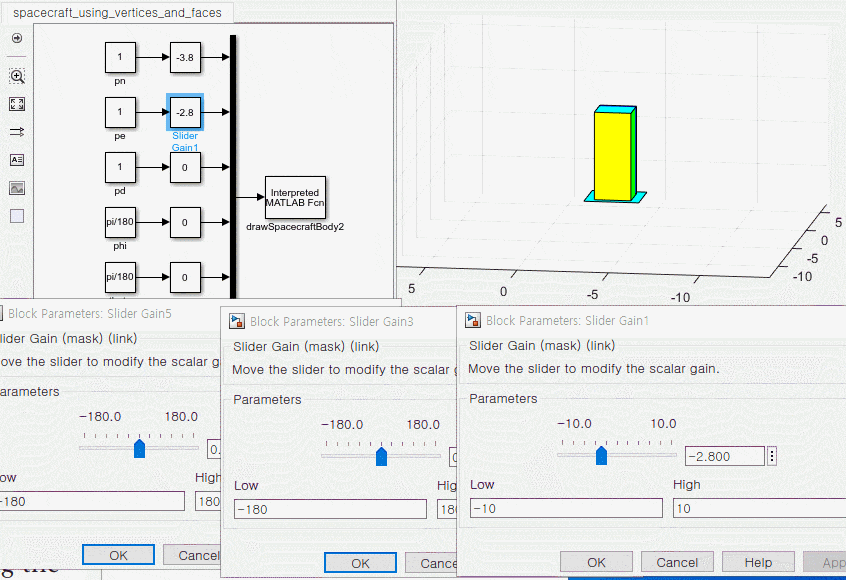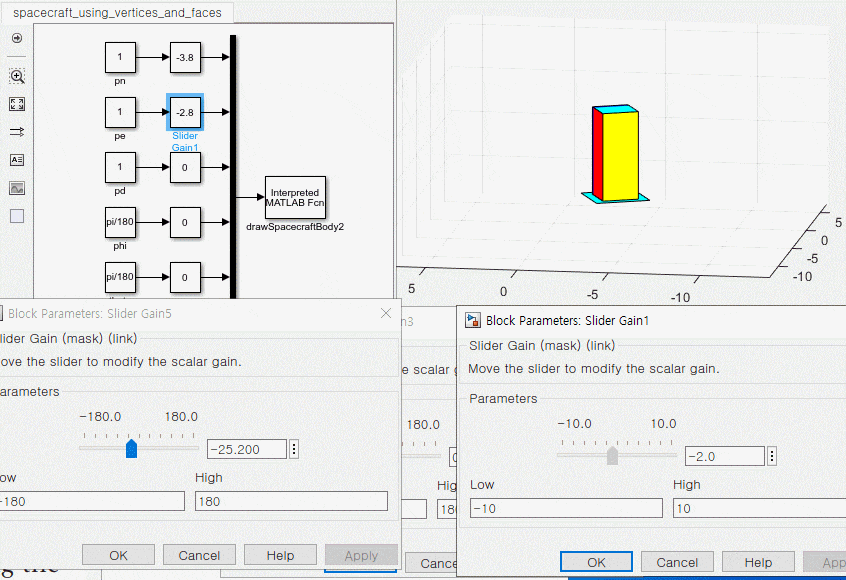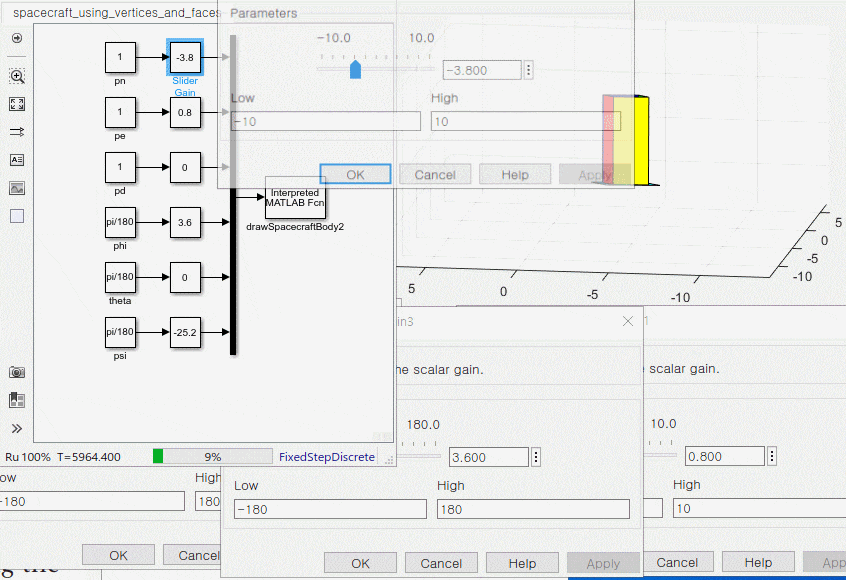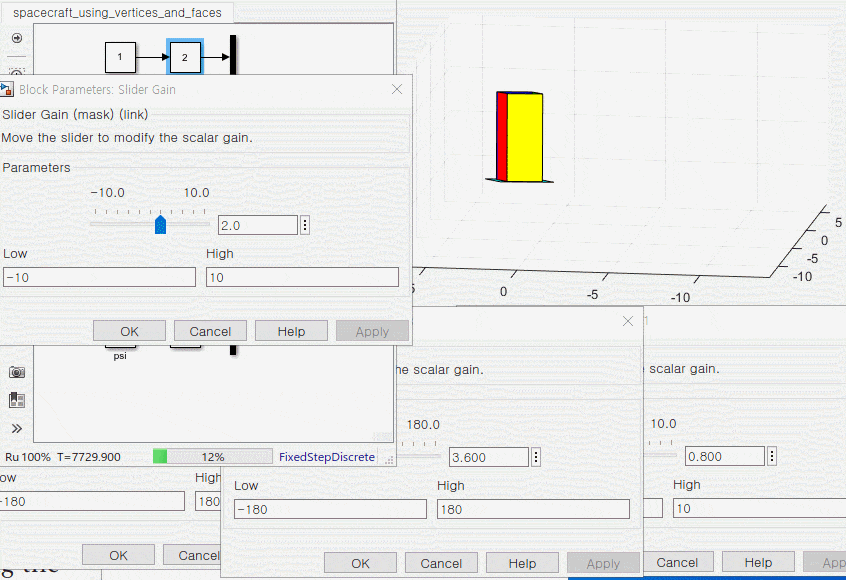
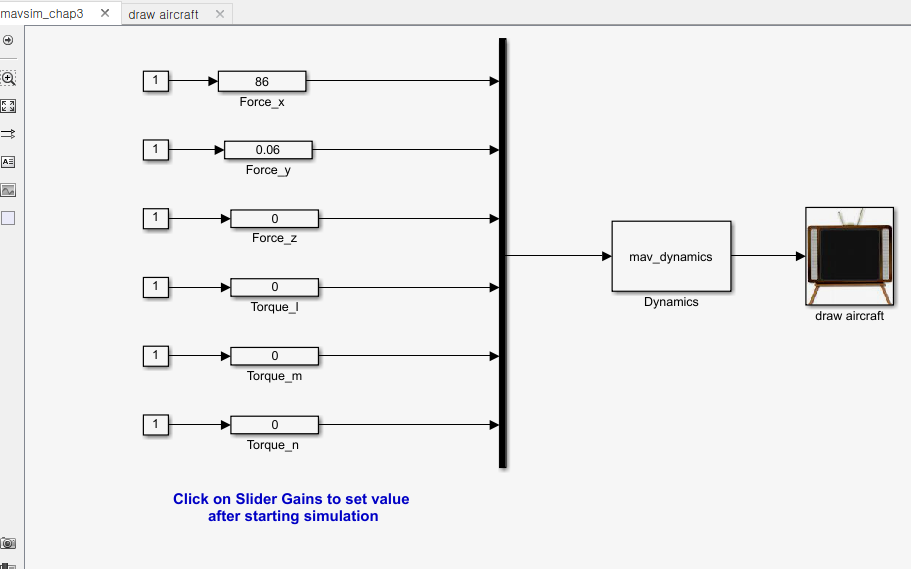
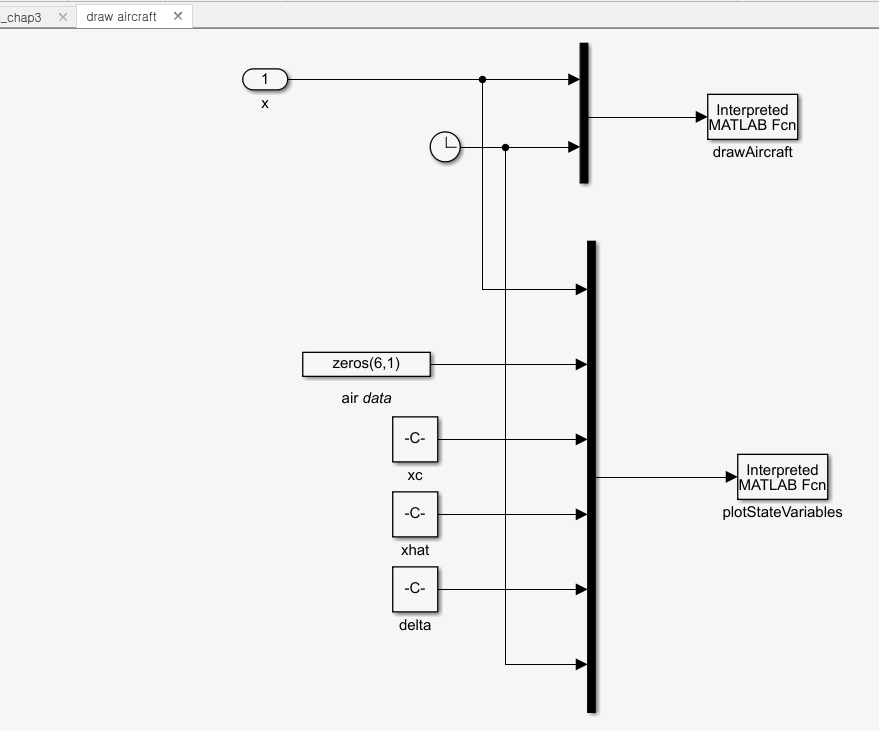
3. 운동 방정식과 애니메이션 블록 연결

1. s 펑션 정리하기

 3장 과제가 부록 F 정리하는건줄 알았는데 s펑션 내용인 부록 E더라.. 왠지 내용이 3장이랑 다른가 싶었는데 아무생각없이 정리하기 바빳다. 

2. 템플릿 완성하기

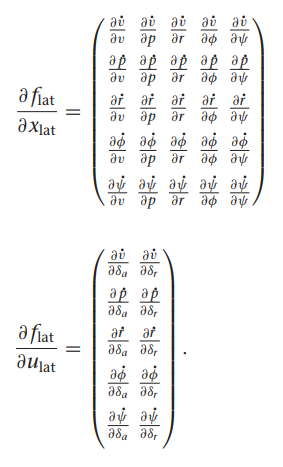
쿼터니언을 이용한 기구학과 동역학식

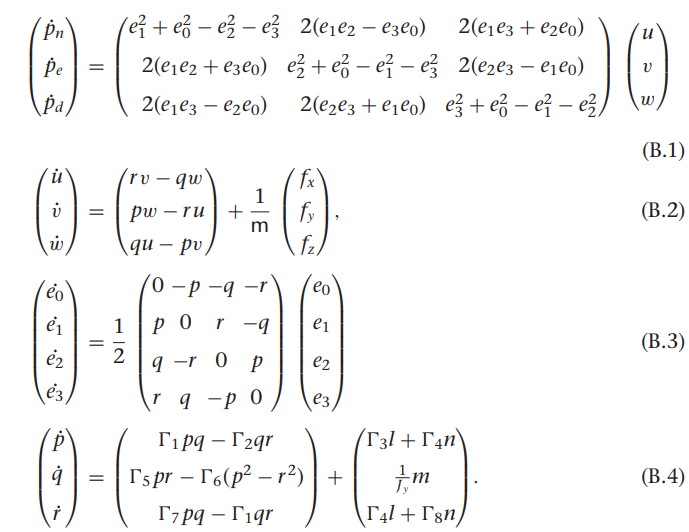
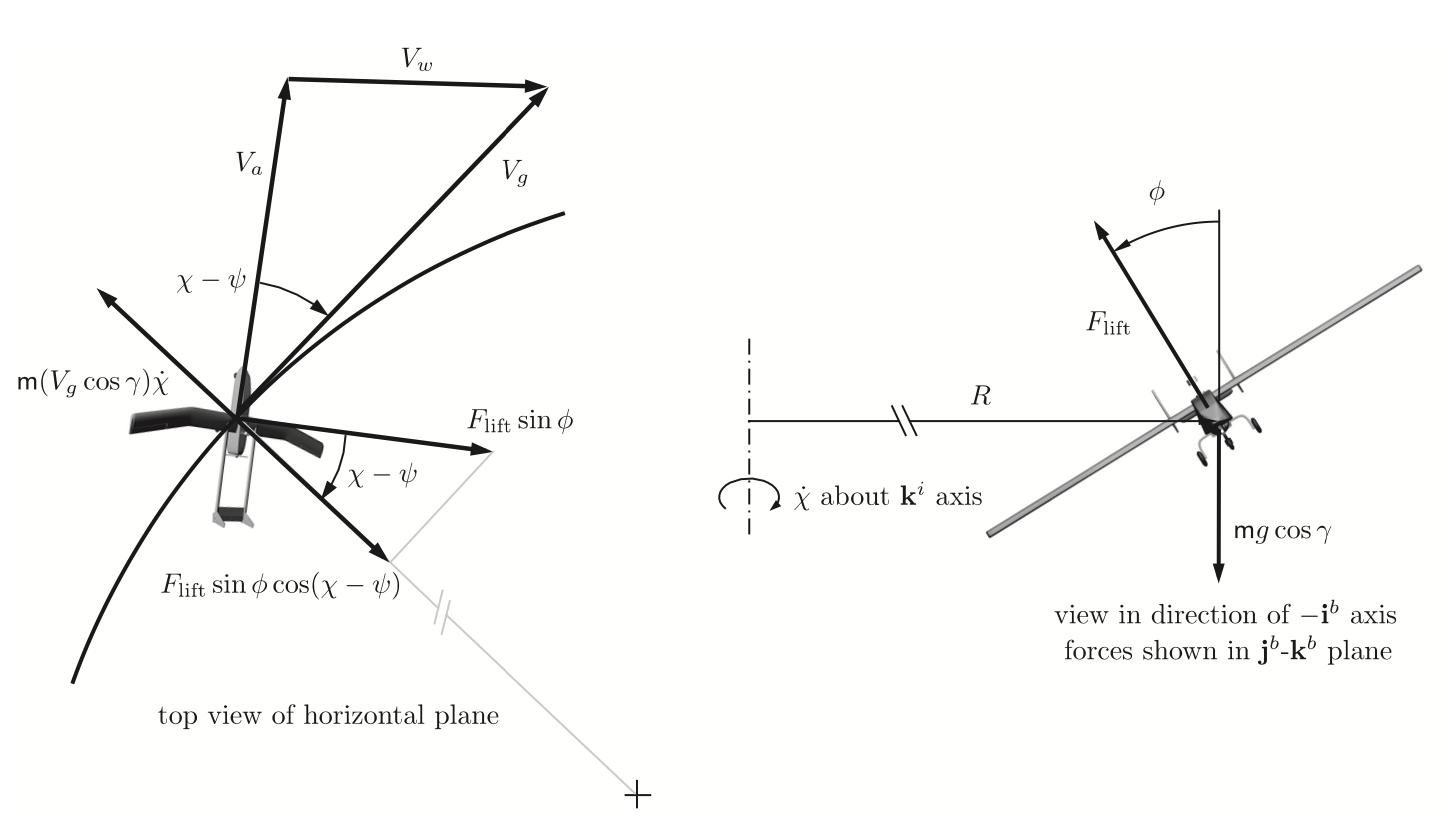
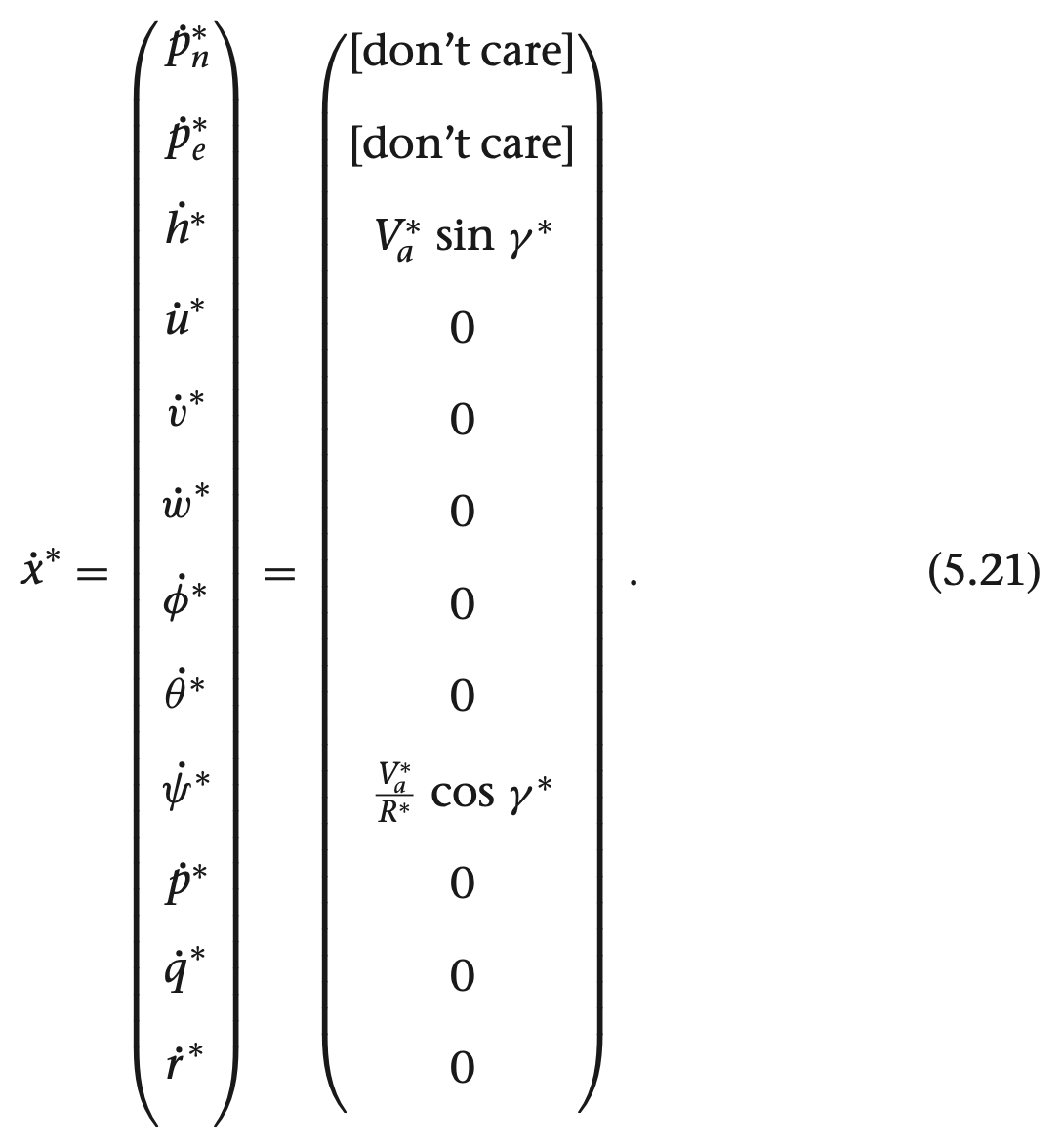
여기서 gamma들 구하는 방법은

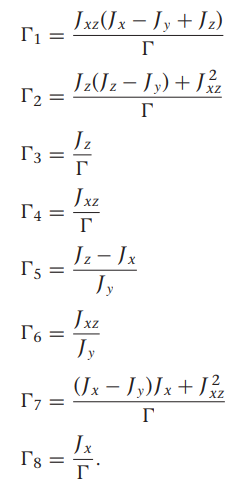
감마 구하는데 필요한 관성모멘트 값은 아래의

우리가 사용하는 비행체 계수들 이용하여 구함

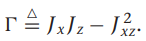
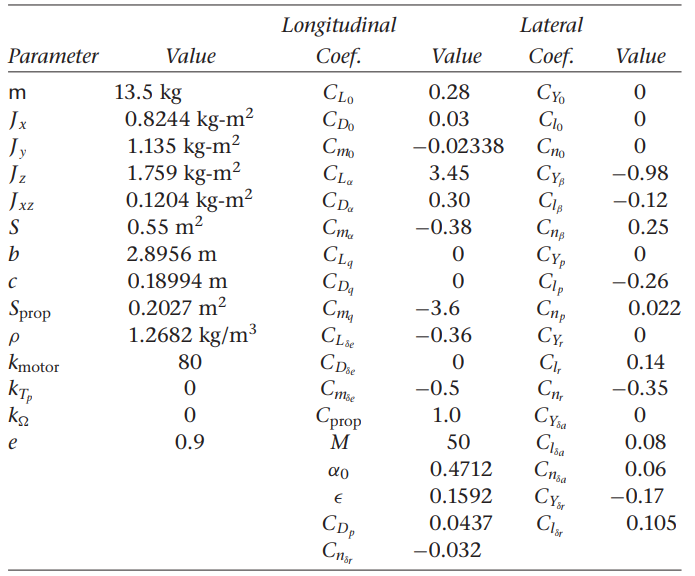
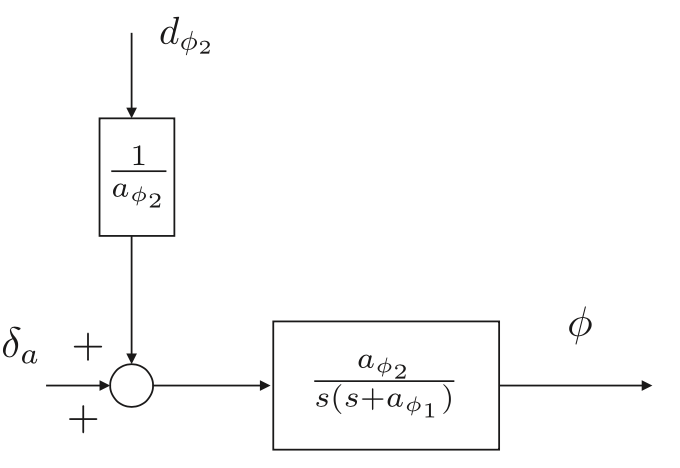
위 기구학, 동역학 식과 비행체 계수에 따라 모델 미분 함수 정리함.

function sys=mdlDerivatives(t,x,uu, MAV)
    pn    = x(1);
    pe    = x(2);
    pd    = x(3);
    u     = x(4);
    v     = x(5);
    w     = x(6);
    e0    = x(7);
    e1    = x(8);
    e2    = x(9);
    e3    = x(10);
    p     = x(11);
    q     = x(12);
    r     = x(13);
    fx    = uu(1);
    fy    = uu(2);
    fz    = uu(3);
    ell   = uu(4);
    m     = uu(5);
    n     = uu(6);
    
    pndot = e1^2+e0^2-e2^2-e3^2*u + 2*v*(e1*e2 - e3*e0) + 2*w*(e1*e3 + e2*e0);
    
    pedot = 2*u*(e1*e2+e3*e0)+v*(e2^2+e0^2-e1^2-e3^2) + w*2*(e2*e3-e1*e0);
    
    pddot = u*2*(e1*e3-e2*e0) + 2*v*(e2*e3 + e1*e0) + w*(e3^2+e0^2 - e1^2 - e2^2);
    
    udot = r*v - q*w + 1/MAV.mass*fx;
    
    vdot = p*w - r*u + 1/MAV.mass*fy;
    
    wdot = q*u - p*v + 1/MAV.mass*fz;
       
    e0dot = 1/2*(-p*e1 -q*e2 -r*e3);
    e1dot = 1/2*(p*e0 + r*e2 -q*e3);
    e2dot = 1/2*(e0*q+e1*-r+e3*p);
    e3dot = 1/2*(r*e0+q*e1-p*e2);
        
    jx = 0.8244;
    jy = 1.135;
    jz = 1.759;
    jxz = 0.1204;
    
    g=jx*jz-jxz^2;
    g1= (jxz*(jx-jy+jz))/g;
    g2=(jz*(jz-jy) + jxz^2)/g;
    g3=jz/g;
    g4= jxz/g;
    g5= (jz-jx)/jy;
    g6= jxz/jy;
    g7=((jx-jy)*jx+jxz^2)/g;
    g8=jx/g;
    
    pdot = g1*p*q-g2*q*r+g3*ell+g4*n;
    
    qdot = g5*p*r-g6*(p^2-r^2) +1/jy*m;
    
    rdot = g7*p*q - g1*q*r + g4*ell + g8*n;
        

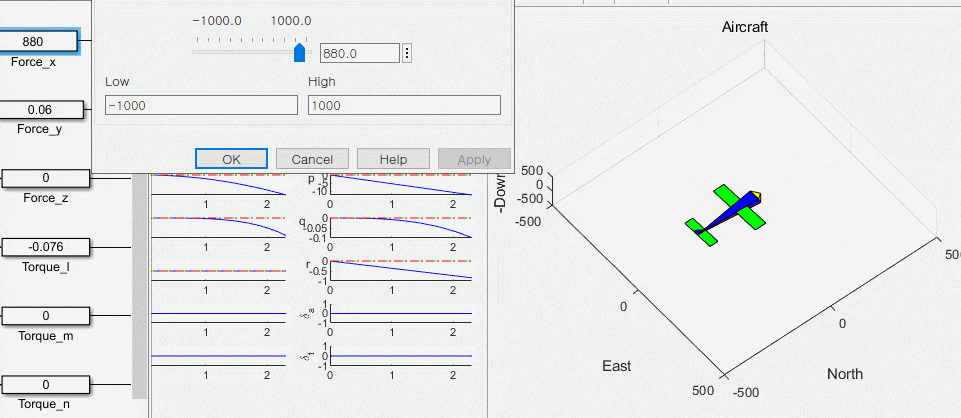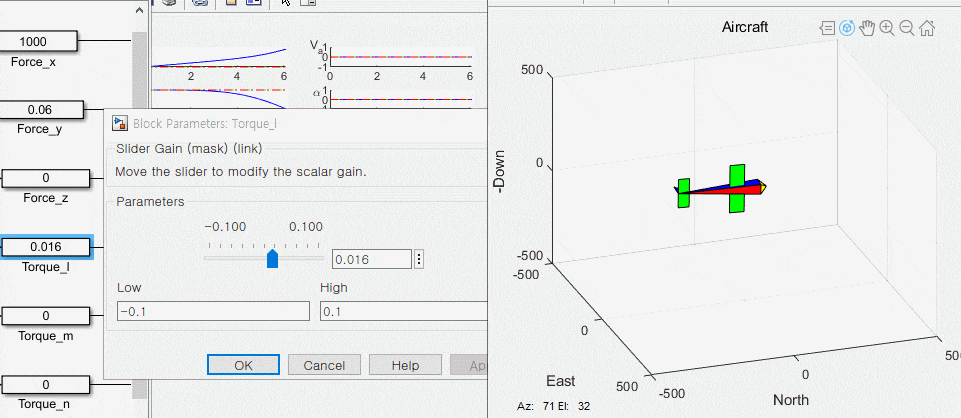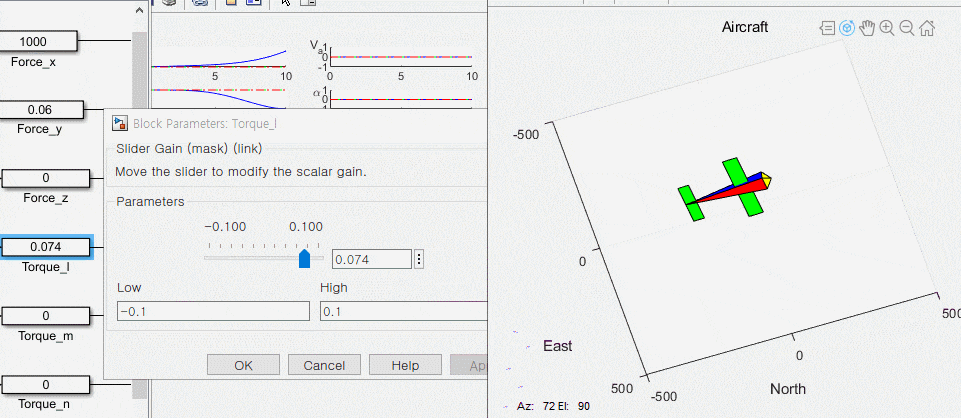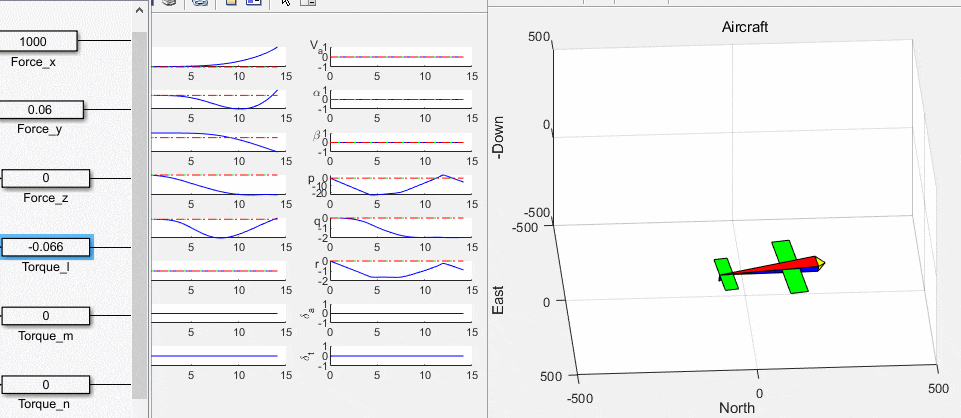
sys = [pndot; pedot; pddot; udot; vdot; wdot; e0dot; e1dot; e2dot; e3dot; pdot; qdot; rdot];

mdlderivative만 했더니 비행체가 움직이질 않는다.

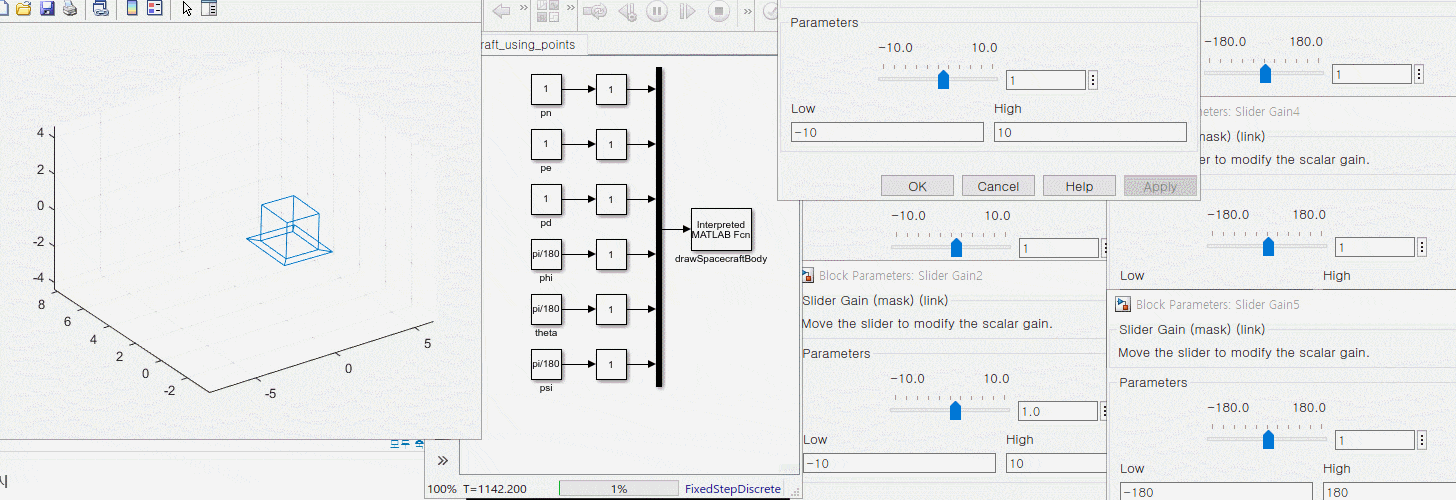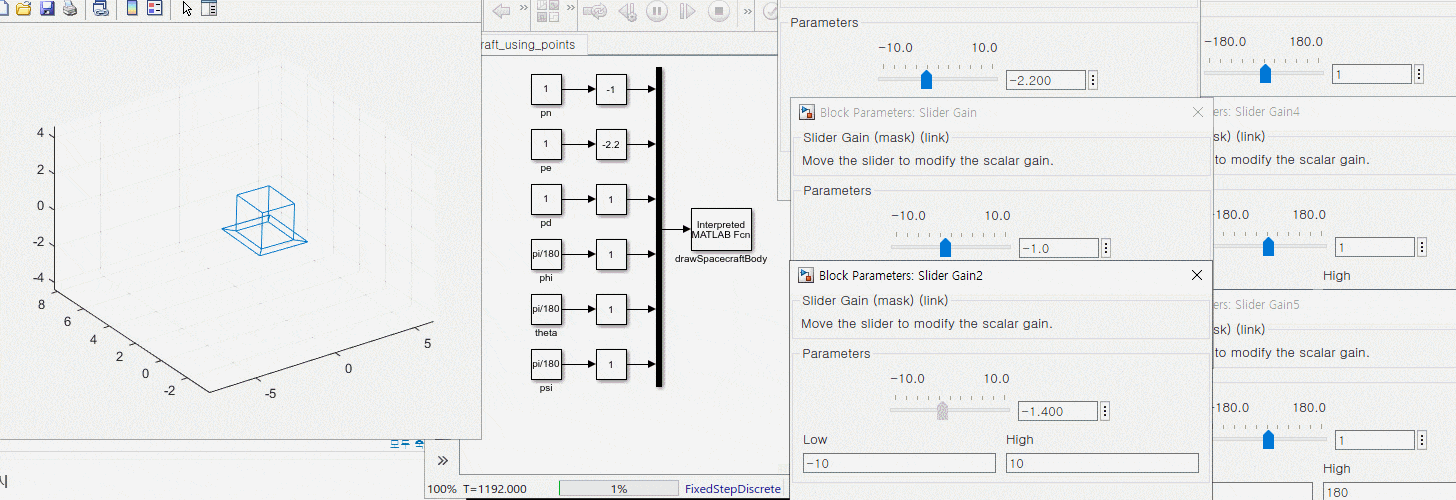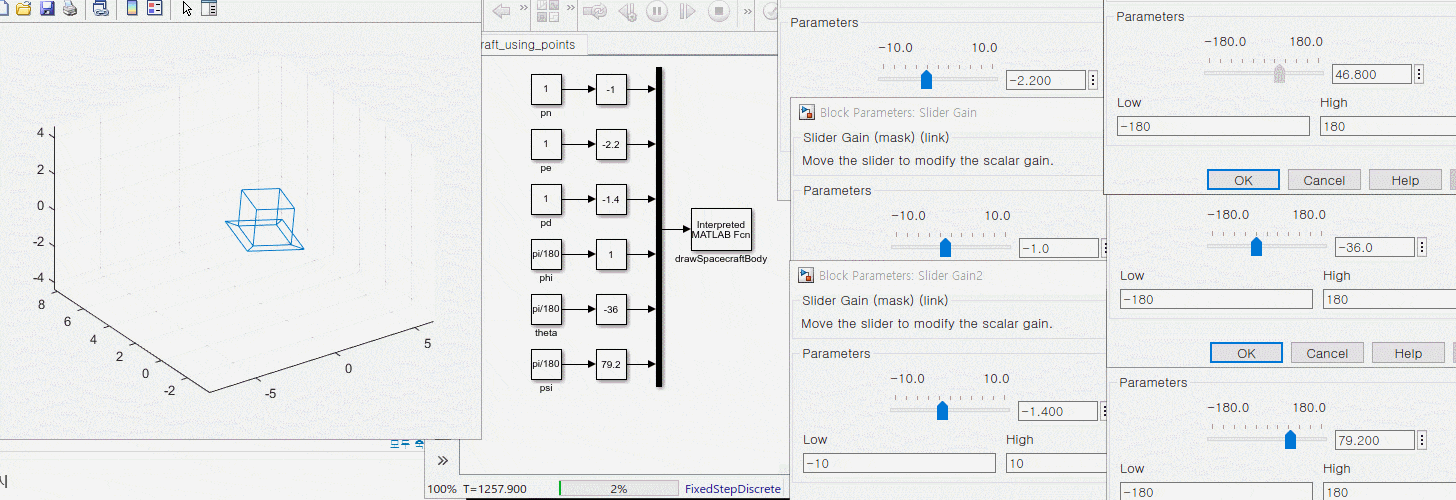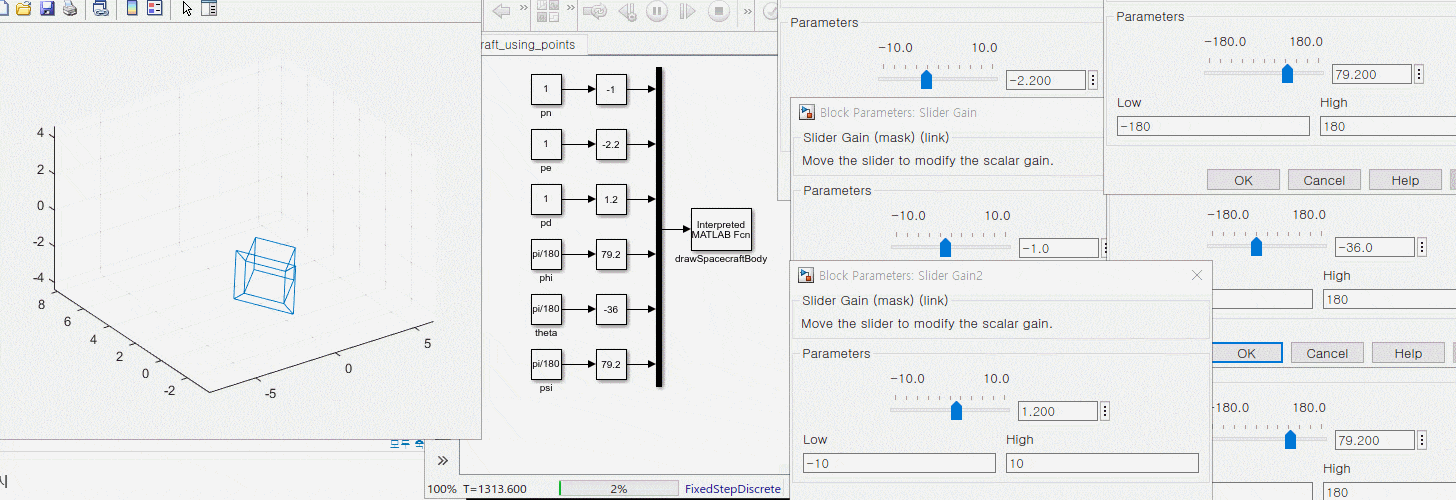
drawAircraft 함수에서 입력값을 확인해보니 전체가 0으로 뜨더라.

mav_dynamics의 출력을 설정안해서 생긴 문제였다.

아래의 초기화 함수를보면 출력 갯수를 12개로 설정했다.

function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes(MAV)

%
% call simsizes for a sizes structure, fill it in and convert it to a
% sizes array.
%
% Note that in this example, the values are hard coded.  This is not a
% recommended practice as the characteristics of the block are typically
% defined by the S-function parameters.
%
sizes = simsizes;

sizes.NumContStates  = 13;
sizes.NumDiscStates  = 0;
sizes.NumOutputs     = 12;
sizes.NumInputs      = 6;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;   % at least one sample time is needed

sys = simsizes(sizes);

%
% initialize the initial conditions
%
x0  = [...
    MAV.pn0;...
    MAV.pe0;...
    MAV.pd0;...
    MAV.u0;...
    MAV.v0;...
    MAV.w0;...
    MAV.e0;...
    MAV.e1;...
    MAV.e2;...
    MAV.e3;...
    MAV.p0;...
    MAV.q0;...
    MAV.r0;...
    ];

%
% str is always an empty matrix
%
str = [];

%
% initialize the array of sample times
%
ts  = [0 0];

% Specify the block simStateCompliance. The allowed values are:
%    'UnknownSimState', < The default setting; warn and assume DefaultSimState
%    'DefaultSimState', < Same sim state as a built-in block
%    'HasNoSimState',   < No sim state
%    'DisallowSimState' < Error out when saving or restoring the model sim state
simStateCompliance = 'UnknownSimState';

% end mdlInitializeSizes

mdlOutputs으로 draw aircraft에서 사용할 변수 12개를 지정해서 출력해주면 된다.

%
%=============================================================================
% mdlOutputs
% Return the block outputs.
%=============================================================================
%
function sys=mdlOutputs(t,x)
    [phi, theta, psi] = Quaternion2Euler([x(7), x(8), x(9), x(10)]);
    y = [...
        x(1);
        x(2);
        x(3);
        x(4);
        x(5);
        x(6);
        phi;
        theta;
        psi;
        x(11);
        x(12);
        x(13);
        ];
sys = y;

% end mdlOutputs

s function 상에서 x는 쿼터니언을 사용하여 총 13개지만

draw Aircraft에서는 오일러각으로 나타내다보니 12개가 된다.

그래서 출력때 Quaternion2Euler 함수로 쿼터니언을 오일러 각으로 변환했다.

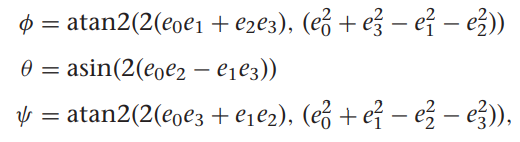
function [phi, theta, psi] = Quaternion2Euler(quaternion)
    % converts a quaternion attitude to an euler angle attitude
    e0 = quaternion(1);
    e1 = quaternion(2);
    e2 = quaternion(3);
    e3 = quaternion(4);
    phi = atan2( 2*(e0*e1 + e2*e3), (e0^2+e3^2 - e1^2 - e2^2));
    theta = asin(2*(e0*e2 - e1*e3) );
    psi = atan2(2*(e0*e3 + e1*e2), (e0*2 + e1^2 - e2^2 - e3^2));
end

 이번장은 매트랩/시뮬링크 환경에 익숙한 사람들을 대상으로 진행하겠습니다. 다세한 정보는 매트랩/시뮬링크 문서를 참조해주시기 바랍니다. 시뮬링크는 상미분 방정식 사이 연결을 푸는대 필수적인 도구입니다.

 시뮬링크 각각의 블록들이 다음의 구조대로 되어있다고 가정해봅시다. 여기서 $x_c$ $\in$ $\mathbb{R}$은 초기 조건이 $x_{c0}$인 연속 상태이고, $x_d$ $\in$ $\mathbb{R}^{n_d}$는 초기 조건이 $x_{d0}$인 이산 상태, u $\in$ $\mathbb{R}^m$는 블록 입력, y $\in$ $\mathbb{R}^p$는 블록의 출력이며, t는 시뮬레이션 경과 시간을 의미합니다.

 s 함수는 다양한 방법으로 정의 가능한 시뮬링크 도구로 여기서 2가지 방법인 레벨 1 m file s함수와 C파일 s 함수에 대해 간단하게 살펴보겠습니다. c 파일 s 함수는 c코드로 컴파일되서 m 파일 s함수 보다 빠르게 실해오딥니다.

D.1 예시 : 2차 미분 방정식

 이 장에서는 표준 2차 전달함수로 시스템을 구현하는 과정을 살펴보겠는데 여기서 레벨 1 m 파일 s 함수와 c 파일 s 함수를 사용하겠습니다.

우선 식 (D.4)를 상태 공간상에 표현하겠습니다. 제어 표준 형태 control canonical form로 나타내면

D.1.1   레벨 1 m 파일 s 함수

식 d.5, d.6을 시스템으로 구현하는 m 파일 s 함수 코드는 아래와 같습니다.

function [sys,x0,str,ts] = second_order_m(t,x,u,flag, zeta,wn)
    switch flag,
    case 0,
        [sys,x0,str,ts]=mdlInitializeSizes;
        % initialize block
        case 1,
        	sys=mdlDerivatives(t,x,u,zeta,wn);
            % define xdot = f(t,x,u)
		case 3,
        	sys=mdlOutputs(t,x,u,wn);
            % define xup = g(t,x,u)
		otherwise,
			sys = [];
		end
	%==========================================================%
	function [sys,x0,str,ts]=mdlInitializeSizes
		sizes = simsizes;
		sizes.NumContStates = 2;
        sizes.NumDiscStates = 0;
        sizes.NumOutputs = 1;
        sizes.NumInputs = 1;
        sizes.DirFeedthrough = 0;
        sizes.NumSampleTimes = 1;
        sys = simsizes(sizes);
        
		x0  = [0; 0];  %  define initial conditions
    	str = [];  % str is always an empty matrix
    	% initialize the array of sample times
    	ts  = [0 0];      % continuous sample time


	%==========================================================%
	function xdot=mdlDerivatives(t,x,u,zeta,wn)
 		xdot(1) = −2*zeta*wn*x(1) − wn^2*x(2) + u;
		xdot(2) = x(1);
    
	%==========================================================%
	function y=mdlOutputs(t,x,u,wn)
    	y = wn^2*x(2);

여기서 첫 줄은 m 파일 함수를 정의하는 부분이 됩니다. 이 함수의 입력은 항상 경과 시간 t, 상태 x(연속 상태와 이산 상태를 연결한), 입력 u, 와 플래그는 기본적으로 있어야 하며, 사용자 정의 입력 파라미터를 추가할 수도 있습니다. 이번 경우에는 $\zeta$와 $\omega_n$을 사용하겠씁니다.

 시뮬링크 엔진은 s 함수를 호출하고 t, x, u, flag를 파라미터로 전달시키는데 flag == 0인경우 시뮬링크 엔진은 sys 구조체를 반환합니다. 여기서 sys 구조체는 초기 상태 x0, 빈 문자열 str, 샘플 타임배열인 ts로 구서오딥니다.

  flag == 1인 경우 시뮬링크 엔진은 f(t, x, u) 함수를 반환하고, flag == 2일때는 g(t, x, u), flag==3 일때는 h(t, x, u)를 반환합니다.

 스위치 문은 flag를 이용해서 적절한 함수를 호출하게 되는데, 초기화 구문을 살펴보면 연속 상태의 수, 이산 상태의 수, 출력 수, 입력의 수를 정의 합니다. 그리고, 출력을 입력으로 피드백 시킬것인지의 여부를 지정할 수도 있습니다. 

블로그에서 제어 공학 등 정리하다보니 수식을 써야 될때가 종종 있다.

찾아보니 latex을 쓰면 된다고 하내

블로그 글에 html 모드로 아래의 스크립트를 집어 넣고

<script type="text/x-mathjax-config">
  MathJax.Hub.Config({
    tex2jax: {
      inlineMath: [ ['$','$'], ["\\(","\\)"] ],
      processEscapes: true
    }
  });
</script>
<script src="https://cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.2/MathJax.js?config=TeX-MML-AM_CHTML"></script>

latex 문법에 따라 작성하면 수식으로 만들어 진다

$a_{1}$	아래첨자
$a^{2}$	위첨자
$\frac{10} {10^{3}}$  분수
$\bar{abc}$ 바
$\dot{def}$ 점
$\approx$ 유사


$\alpha$
$\beta$
$\gamma$
$\theta$

$\frac{\alpha_{min}^{2}} {\dot{\beta_{min}^{3}}}$

위는 작성 예시

아래는 실제 적용 결과

$a_{1}$ 
$a^{2}$ 
$\frac{10} {10^{3}}$  
$\bar{abc}$
$\dot{def}$
$\approx$

$\alpha$
$\beta$
$\gamma$
$\theta$

$\frac{\alpha_{min}^{2}} {\dot{\beta_{min}^{3}}}$

복잡한 문법은 다음 주소에서 참고해서 쓰자 빠잉

https://www.codecogs.com/latex/eqneditor.php

function drawAircraftt(uu)

    % process inputs to function
    pn       = uu(1);       % inertial North position     
    pe       = uu(2);       % inertial East position
    pd       = uu(3);           
    u        = uu(4);       
    v        = uu(5);       
    w        = uu(6);       
    phi      = uu(7);       % roll angle         
    theta    = uu(8);       % pitch angle     
    psi      = uu(9);       % yaw angle     
    p        = uu(10);       % roll rate
    q        = uu(11);       % pitch rate     
    r        = uu(12);       % yaw rate    
    t        = uu(13);       % time

    % define persistent variables 
    persistent aircraft_handle;
    persistent Vertices
    persistent Faces
    persistent facecolors
    
    % first time function is called, initialize plot and persistent vars
    if t==0
        figure(1), clf
        [Vertices, Faces, facecolors] = defineAircraft;
        aircraft_handle = drawAircraftBody(Vertices,Faces,facecolors,...
                                               pn,pe,pd,phi,theta,psi,...
                                               [],'normal');
        title('Aircraft')
        xlabel('East')
        ylabel('North')
        zlabel('-Down')
        view(32,47)  % set the vieew angle for figure
        axis([-500,500,-500,500,-500,500]);
        hold on
        
    % at every other time step, redraw base and rod
    else 
        drawAircraftBody(Vertices,Faces,facecolors,...
                           pn,pe,pd,phi,theta,psi,...
                           aircraft_handle);
    end
end

  
%=======================================================================
% drawAircraft
% return handle if 3rd argument is empty, otherwise use 3rd arg as handle
%=======================================================================
%
function handle = drawAircraftBody(V,F,patchcolors,...
                                     pn,pe,pd,phi,theta,psi,...
                                     handle,mode)

  V = rotate(V', phi, theta, psi);  % rotate Aircraft

  V = translate(V, pn, pe, pd);  % translate Aircraft
  % transform vertices from NED to XYZ (for matlab rendering)
  R = [...
      0, 1, 0;...
      1, 0, 0;...
      0, 0, -1;...
      ];
  V = V'*R;
  if isempty(handle)
      handle = patch('Vertices', V, 'Faces', F,...
                     'FaceVertexCData',patchcolors,...
                     'FaceColor','flat',...
                     'EraseMode', mode);
       grid on;
  else
    set(handle,'Vertices',V,'Faces',F);
    drawnow
  end
end

%%%%%%%%%%%%%%%%%%%%%%%
function XYZ=rotate(XYZ,phi,theta,psi)
  % define rotation matrix
  R_roll = [...
          1, 0, 0;...
          0, cos(phi), -sin(phi);...
          0, sin(phi), cos(phi)];
  R_pitch = [...
          cos(theta), 0, sin(theta);...
          0, 1, 0;...
          -sin(theta), 0, cos(theta)];
  R_yaw = [...
          cos(psi), -sin(psi), 0;...
          sin(psi), cos(psi), 0;...
          0, 0, 1];
  R = R_roll*R_pitch*R_yaw;
  % rotate vertices
  XYZ = R*XYZ;
end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% translate vertices by pn, pe, pd
function XYZ = translate(XYZ,pn,pe,pd)
  XYZ = XYZ + repmat([pn;pe;pd],1,size(XYZ,2));
end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% define aircraft vertices and faces
function [V,F,facecolors] = defineAircraft()

% Define the vertices (physical location of vertices
V = [...
    75, 0, 0;...       % pt 1
    50, 25, -25;...    % pt 2
    50, -25, -25;...   % pt 3
    50, -25, 25;...    % pt 4
    50, 25, 25;...     % pt 5
    -225, 0, 0;...      % pt 6
    0, 125, 0;...       % pt 7
    -50, 125, 0;...      % pt 8
    -50, -125, 0;...     % pt 9
    0, -125, 0;...      % pt 10
    -187.5, 75, 0;...   % pt 11
    -225, 75, 0;...    % pt 12
    -225, -75, 0;...   % pt 13
    -187.5, -75, 0;...  % pt 14
    -187.5, 0, 0;...     % pt 15
    -225, 0, -62.5;...  % pt 16
    ];

% define faces as a list of vertices numbered above
  F = [...
        1, 1, 2, 5;...  % nose right
        1, 1, 3, 4;...  % nose left
        1, 1, 2, 3;...  % nose upper
        1, 1, 4, 5;...  % nose bottom
        2, 5, 6, 6;...  % fuselage right
        3, 4, 6, 6;...  % fuselage left
        2, 3, 6, 6;...  % fuselage upper
        4, 5, 6, 6;...  % fuselage bottom
        7, 8, 9, 10;...  % wing
        11, 12, 13, 14;...  % horizontal tail
        6, 15, 16, 6;...  % vertical tail
        ];

% define colors for each face    
  myred = [1, 0, 0];
  mygreen = [0, 1, 0];
  myblue = [0, 0, 1];
  myyellow = [1, 1, 0];
  mycyan = [0, 1, 1];

  facecolors = [...
    myyellow;...    % nose right
    myyellow;...    % nose left
    myyellow;...    % nose upper
    myyellow;...    % nose bottom
    myblue;...      % fuselage right
    myblue;...      % fuselage left
    myblue;...      % fuselage upper
    myred;...      % fuselage bottom
    mygreen;...     % wing
    mygreen;...     % horizontal tail
    myblue;...      % vertical tail
    ];
end
  

시뮬링크 애니메이션

 비행 동역학 제어기 학습에서 비행체의 운동을 시각화 할수 있어야 합니다. 이번 장에서는 매트립과 시뮬링크에서 애니메이션을 만드는 방법을 살펴보겠습니다

C.1 매트랩에서 그래픽 핸들

 매트랩에서 plot 같은 그래픽 함수를 사용할떄 이 함수들은 plot에 대한 핸들 hanlde을 반환합니다. 그래픽 핸들은 C/C++에서 포인터와 비슷한 개념인데, plot의 설정에 접근할수 있게 만들어 줍니다.

 예를 들어 매트랩 입력을 준다면

>> plot_handle=plot(t,sin(t))

 이는 sin(t)의 plot에 대한 포인터(핸들) 반환합니다. 플롯의 설정값들은 plot 명령에다가 추가로 적기 보다는 handle을 이용해서 보통 바꾸게 됩니다. 예를들면

>> set((plot_handle, 'YData', cos(t))

 는 cos(t)에 대한 플롯을 축이나, 타이틀, 라밸 등 다른 요소들을 다시 작성하지 않고, 해당 plot을 변경시킵니다. 만약 플롯이 여러 물체의 그래프를 포함하고 있다면, 핸들을 이용해서 각 오브젝트에 접근할수 있습니다. 예를들면

>>  plot_handle1 = plot(t,sin(t))

>> hold_on

>> plot_handle2 = plot(t,cos(t))

 sin(t), cos(t)를 같은 플롯에다가 그리고 각각의 오브젝트에 대한 핸들을 구하였습니다. 이 오브젝트들은 핸들을 이용해서 다시 그릴 필요 없이 별개로 변경 시킬수 있습니다. 예를들어 cos(t)를 cos(2t)로 바꿀경우 명령은

>> set(plot_handle2, 'YData', cos(2*t) )

 앞으로 우리는 이것을 이용해서 시뮬링크 시뮬레이션을 시간 변화에 따른 애니메이션을 그릴건데, C.2에서 2차원 역 도립진자를 C.3에서 3차원 우주선 애니메이션을, C.4에선 우주선 애니메이션을 점과 면 데이터로 생성해보겠습니다.

C.2 역도립진자 애니메이션 예제

 그림 C.1의 역 도립진자를 보면, 설정 값으로 카트의 위치 y, 막대 각 $\theta$가 있고, 물리적 파라미터로 막대 길이 L, 몸체 폭 w, 몸체 높이 h, 그리고 지상과 몸체 사이의 갭인 g로 이루어집니다. 첫번째로 해야 할 일은 이 애니메이션을 그리는 점들의 위치를 결정해야 하는데, 역 도립진자의 경우 베이스 몸체의 4개의 점

 과 막대의 두 점을 아래와 같이 정리할 수 있습니다.

 베이스와 막대는 독립적으로 움직이므로, 각각을 피겨 핸들로 다루겠습니다. 우선 drawBase 명령을 아래의 매트랩 코드로 구현하겠습니다.

function handle = drawBase(y, width, height, gap, handle, mode)
    X = [y-width/2, y+width/2, y+width/2, y-width/2];
    Y = [gap, gap, gap+height, gap+height];
    if isempty(handle),
       	handle = fill(X, Y, 'm', 'EraseMode', mode);
    else
        set(handle, 'XData', X, 'Ydata', Y);
    end

 1. 핸들을 입력과 출력으로 설정

 2. 베이스의 코너 점들의 X, Y 위치를 정의

 3. 핸들이 존재하지 않으면 fill명령어로 그림

 4. 핸들이 존재하면 set으로 다시 설정

막대를 그리는 매트랩 코드는 비슷하게 다음과 같이 그립니다.

function handle = drawRod(y, theta, L, gap, height, handle, mode)
    X = [y, y+L*sin(theta)];
    Y = [gap+height, gap+height + L*cos(theta)];
    if isempty(handle),
       	handle = fill(X, Y, 'g', 'EraseMode', mode);
    else
        set(handle, 'XData', X, 'Ydata', Y);
    end

 파라미터 mode는 매트랩에서 EraseMode를 명시해주는데 사용하는데, EraseMode는 normal, none, xor, background 등을 설정할 수 있습니다. 이 모드들의 차이는 매트랩 핼프데스크에서 Image Properties를 보시면 찾을수 있습니다.

 팬듈럼 애니메이션의 메인 루틴은 다음과 같습니다.

function handle = drawPendulum(u)
    % process inputs to function
    y		= u(1);
    theta	= u(2);
    t		= u(3);
    
    % drawing parammeters
    L = 1;
    gap = 0.01;
    width = 1.0;
    height = 0.1;;
    
    %define persistent variables
    persistent base_handle
    persistent rod_handle
    
    % first time function is called, initialize plot
    % and peersistent vars
    if t==0,
        figure(1), clf
        track_width=3;
        plot([-track_width,track_width], [0,0], 'k');
        hold on
        base_handle = drawBase(y, width, height, gap, [], 'normal');
        rod_handle = drawRod(y, theta, L, gap, height, [], 'normal');
        axis([-track_width, track_width, -L, 2*track_width-L]);
    % at every other time step, redraw base and rod
    else
        drawBase(y, width, height, gap, base_handle);
        drawRod(y, theta, L, gap, height, rod_handle);
    end
    

 이 drawPendulum 루틴을 그림 C.2처럼 시뮬링크 파일에서 호출하겠습니다. 여기서 3개의 입력 값으로 위치 y, 각 $\theta$, 시간 t를 사용하겠습니다.

 위 코드를 정리하면

 1. 입력 u를 y, $\theta$, t로 이름 재설정

 2. 그림 파라미터 설정

 3. 그래픽 핸들 유지(persistent)

 4. 처음 호출되면 애니메이션 초기화

 5. 이후 입력에 대해 다시 그리기

C.3 애니메이션 예제: 선을 이용한 우주선

 이전 장에서는 단순한 2차원 애니메이션을 다뤘다면 이번에는 6자유도를 가지는 3차원 우주선에 대해서 살펴보겠습니다. 그림 C.3은 선을 이용해서 그린 간단한 우주선으로 바닥은 태양을 향하는 태양광 패널이 됩니다. 

 첫번째로 할 일은 우주선의 각 점들을 라벨링하고, 동체 고정 좌표계 상에서 각점들의 좌표를 정해야 합니다. 표준 항공역학 축을 따라 X 축은 우주선의 정면, Y축은 우주선의 오른쪽, Z축은 바닥을 향하게 됩니다. 그림 C.3에서 점 1~12가 라밸 되어있고, 각각의 좌표들이 명시되어있습니다. 선을 만들기 위해서 이 점들을 연결시키면 되는데, 연속적인 선들로 만들기 위해 다음 순서대로 노드들을 평행이동 시키겠습니다. 1-2-3-4-1-5-6-2-6-7-3-7-8-4-8-5-1-9-10-2-10-11-3-11-12-4-12-9. 우주선의 지역 좌표계를 매트랩으로 구현하면 다음과 같습니다.

function XYZ=spacecraftPoints
 % define points on the spacecraft in local NED coordinates
 XYZ = [...
 1 1 0;... % point 1
 1 −1 0;... % point 2
 −1 −1 0;... % point 3
 −1 1 0;... % point 4
 1 1 0;... % point 1
 1 1 −2;... % point 5
 1 −1 −2;... % point 6
 1 −1 0;... % point 2
 1 −1 −2;... % point 6
 −1 −1 −2;... % point 7
 −1 −1 0;... % point 3
 −1 −1 −2;... % point 7
 −1 1 −2;... % point 8
 −1 1 0;... % point 4
 −1 1 −2;... % point 8
 1 1 −2;... % point 5
 1 1 0;... % point 1
 1.5 1.5 0;... % point 9
 1.5 −1.5 0;... % point 10
 1 −1 0;... % point 2
 1.5 −1.5 0;... % point 10
 −1.5 −1.5 0;... % point 11
 −1 −1 0;... % point 3
 −1.5 −1.5 0;... % point 11
 −1.5 1.5 0;... % point 12
 −1 1 0;... % point 4
 −1.5 1.5 0;... % point 12
 1.5 1.5 0;... % point 9
]';

 우주선의 상태들로 오일러각 $\phi$, $\theta$, $\psi$가 있으며 이는 롤, 피치, 요 각도를 의미하고, $p_n$, $p_d$, $p_d$는 북, 동, 아래 방향을 의미합니다. 우주선의 점들은 다음의 매트랩 코드를 이용하여 회전과 평행이동을 하게 됩니다.

function XYZ=rotate(XYZ,phi,theta,psi)
 % define rotation matrix
 R_roll = [...
 1, 0, 0;...
 0, cos(phi), −sin(phi);...
 0, sin(phi), cos(phi)];
 
 R_pitch = [...
 cos(theta), 0, sin(theta);...
 0, 1, 0;...
 −sin(theta), 0, cos(theta)];
 
 R_yaw = [...
 cos(psi), −sin(psi), 0;...
 sin(psi), cos(psi), 0;...
 0, 0, 1];
 
 R = R_roll*R_pitch*R_yaw;
 % rotate vertices
 XYZ = R*XYZ;

function XYZ = translate(XYZ,pn,pe,pd)
 XYZ = XYZ + repmat([pn;pe;pd],1,size(XYZ,2));

 원하는 자세로 우주선을 그리기위해 다음의 매트랩 코드를 작성합시다.

function handle = drawSpacecraftBody(pn,pe,pd,phi,theta,psi, handle, mode)
 % define points on spacecraft in local NED
 %coordinates
 NED = spacecraftPoints;
 % rotate spacecraft by phi, theta, psi
 NED = rotate(NED,phi,theta,psi);
 % translate spacecraft to [pn; pe; pd]
 NED = translate(NED,pn,pe,pd);
 % transform vertices from NED to XYZ
 R=[...
 0, 1, 0;...
 1, 0, 0;...
 0, 0, −1;...
 ];
 XYZ = R*NED;
 % plot spacecraft
 if isempty(handle),
   handle = plot3(XYZ(1,:),XYZ(2,:),XYZ(3,:), `EraseMode', mode);
 else
   set(handle,`XData',XYZ(1,:),`YData',XYZ(2,:),`ZData',XYZ(3,:));
   drawnow
 end

 위 식에서 plot3은 처음 우주선을 그리는 명령이고, set으로 X,Y,ZData를 변경하며, 이 우주선을 그린 결과는 C.4가 됩니다.

 spacecraftPoints 함수로 애니메이션 구현시 문제점은 애니메이션이 갱신될때마다 이 함수가 호출되게 됩니다. 이 점은 정적이므로, 한번만 정의하면 되기 때문에 시뮬레이션 시작시 마스크 함수를 써서 정의해 주면 됩니다. drawSpacecraft m file을 마스킹하려면 edit mask를 클릭하고 그림 C.5처럼 입력해주면 됩니다. 이러면 우주선의 점들이 초기화 시점에서 정의되어 drawSpacecraft 파일의 파라미터로 사용됩니다.

수정 코드

function handle = drawSpacecraftBody(u)
persistent spacecraft_handle; 
pn = u(1);
pe = u(2);
pd = u(3);
phi = u(4);
theta = u(5);
psi = u(6);
% define points on spacecraft in local NED
NED=spacecraftPoints;
 % rotate spacecraft by phi, theta, psi
 NED = rotate(NED,phi,theta,psi);
 % translate spacecraft to [pn; pe; pd]
 NED = translate(NED,pn,pe,pd);
 % transform vertices from NED to XYZ
 R=[0, 1, 0;
     1, 0, 0;
     0, 0, -1];
 XYZ = R*NED;
 % plot spacecraft
 if isempty(spacecraft_handle),
   spacecraft_handle = plot3(XYZ(1,:),XYZ(2,:),XYZ(3,:), 'eraseMode',  'normal');
   grid on;
 else
   set(spacecraft_handle,'XData',XYZ(1,:),'YData',XYZ(2,:),'ZData',XYZ(3,:));
   drawnow
 end

C.4 애니메이션 예제 : 점과 면을 이용한 우주선

 그림 C.4은 점과 면 구조로 vertex-face 로 구현할수 있는데, plot3 대신 patch 명령을 사용합니다. 점들과, 면, 색상을 다음의 코드로 정의 합니다.

function [V, F, patchcolors]=spacecraftVFC
% Define the vertices (physical location of vertices
V=[...
1 1 0;... % point 1
1 -1 0;... % point 2
-1 -1 0;... % point 3
-1 1 0;... % point 4
1 1 -2;... % point 5
1 -1 -2;... % point 6
-1 -1 -2;... % point 7
-1 1 -2;... % point 8
1.5 1.5 0;... % point 9
1.5 -1.5 0;... % point 10
-1.5 -1.5 0;... % point 11
-1.5 1.5 0;... % point 12
];

% define faces as a list of vertices numbered above
F=[...
1, 2, 6, 5;... % front
4, 3, 7, 8;... % back
1, 5, 8, 4;... % right
2, 6, 7, 3;... % left
5, 6, 7, 8;... % top
9, 10, 11, 12;... % bottom
];
% define colors for each face
myred = [1, 0, 0];
mygreen = [0, 1, 0];
myblue = [0, 0, 1];
myyellow = [1, 1, 0];
mycyan = [0, 1, 1];
patchcolors = [...
    myred;... % front
    mygreen;... % back
    myblue;... % right
    myyellow;... % left
    mycyan;... % top
    mycyan;... % bottom
];

 그림 C.3처럼 점들을 설정하고, 면들을 정의 하였는데 정면의 경우 점 1-2-6-5 으로 만들었습니다. 각 면들의 색상도 정의하고 비행체 그리는 코드를 아래와 같이 정리하였습니다.

function handle = drawSpacecraftBody2(u)
persistent spacecraft_handle;

pn = u(1);
pe = u(2);
pd = u(3);
phi = u(4);
theta = u(5);
psi = u(6);

[V, F, patchcolors] = spacecraftVFC;
% define points on spacecraft
V = rotate(V', phi, theta, psi)';
% rotate spacecraft
V = translate(V', pn, pe, pd)';
% translate spacecraft
R=[...
    0, 1, 0;...
    1, 0, 0;...
    0, 0, -1;...
];

V=V*R; % transform vertices from NED to XYZ
if isempty(spacecraft_handle),
    spacecraft_handle = patch('Vertices', V, 'Faces', F, ...
    'FaceVertexCData',patchcolors,...
    'FaceColor','flat',...
    'EraseMode', 'normal');
    grid on;
else
    set(spacecraft_handle,'Vertices',V,'Faces',F);
end

6.3 횡방향 오토파일럿

 그림 6.6은 연속 폐루프를 이용한 횡방향 오토파일럿의 블록다이어그램을 보여주는데 여기에 5가지의 게인이 존재합니다. 먼저 미분 게인 $k_{d_{\phi}}$는 가장 안쪽 루프에서 롤 변화율 댐핑을 제공하고, 롤 자세는 비례, 적분 게인인 $k_p_{\phi}$와 $k_{i_{\phi}}$로 제어할 수 있습니다.

 방위각은 비례, 적분 게인 $k_{p_{\chi}}$와 $k_{i_{\chi}}$로 제어할 수 있는데, 연속 폐루프의 게인은 내부에서부터 시작하여 외부로 연속적으로 나아가는 점에 따라 우선 $k_{d_{\phi}}$, $k_{p_{\phi}}$를, 두번째로 $i_{\phi}$, 마지막으로 $k_{p_{\chi}}$, $k_{i_{\chi}}$를 선택합니다.

6.3.1 롤 자세 루프 설계

 횡방향 오토파일럿에서 내부 루프는 롤각과 롤 변화율을 제어하는데 사용되는데 그림 6.7과 같습니다. 만약 전달함수 계수 $a_{\phi_1}$과 $a_{\phi_2}$를 안다면, 폐루프 응답을 이용하여 제어기 게인 $k_{d_{\phi}}$와 $k_{p_{\phi}}$를 선택하는 방법이 있습니다. 그림 6.7에서 $\phi^c$로부터 $\phi$에 대한 전달함수는 아래와 같이 주어지는데

 DC 게인이 1과 같은 점을 고려할때 원하는 응답이 다음의 표준 2차 전달함수 형태로 주어지면

분모의 계수를 같다고 한다면 다음의 식을 얻을수 있습니다.

 식 (6.2)을 보면 비례 게인은 롤 오차가 $e_{\phi}^{max}$일때 에일러론이 포화되도록 선택되므로 식 (6.2)로 다음과 같이 정리할 수 있습니다. 이때 $e_{\phi}^{max}$는 설계 파라미터 입니다.

 롤 루프의 고유주파수는 그러므로 아래와 같으며

$k_{d_{\phi}}$에 대해 식 (6.6)을 풀면 다음과 같습니다. 여기서 댐핑 비 $\zeta_{\phi}$는 설계 파라미터가 입니다..

롤 적분기 

 그림 6.7에서 개루프 전달함수는 하나의 시스템으로 영 정상상태 롤 오차는 적분기 없이 수행되야 합니다. 그림 5.2에서는 $\deta_a$ 전에 요란이 합쳐져 들어가는걸 볼수 있었는데, 이 요란은 롤 역학의 선형, 차수 감소 모델을 만드는 과정에서 무시되는 요소였습니다. 그래서 이 시스템에서는 돌풍이나 난기류 같은 물리적인 동요로 사용할 수 있습니다. 그림 6.8은 요란을 추가한 롤 루프로, 여기서 $\phi$(s)를 풀면 다음과 같습니다.

 $d_{phi_2}$는 최종값 정리 final value theorem로 구하는 일정한 요란으로 $d_{\phi_2}$ = A/s 이며,  $d_{\phi_2}$ 때문에 정상상태 오차는 $\frac{A} {a_{\phi_2} k_{p_{\phi}}}$가 됩니다.

 일정한 궤적에서 p, q, r은 일정할 것이며 $d_{\phi}$ 또한 일정한 값이 될건데, 식 (5.25)에서 볼수 있습니다. 그러므로 적분기로 정상상태 오차를 제거하는것이 좋습니다.

 그림 6.9는 요란 $d_{\phi_2}$을 제거하기위해 적분기를 추가한 롤 자세 유지 루프가 됩니다.

그림 6.9에서 $\phi$(s)에 대하여 풀면

 이 경우 최종값 정리에 따라 상수 $d_{\phi}$에 대한 영정상상태 오차를 예측하게 됩니다. $d_{\phi}$가 램프 입력이라면 정상상태 오차는 $\frac{A} {a_{\phi_2} k_{i_{\phi}}}$가 됩니다. $a_{\phi_1}$과 $a_{\phi_2}$를 안다면 루트 로커스로 $k_{i_{\phi}}$를 쉽게 구할수 있습니다. 폐루프의 극점은 

에반스 폼으로 바꾸면

 그림 6.10은 $k_{i_{\phi}}$ 함수에 대해 특성 방정식의 루트로커스를 띄운 것으로, 작은 게인 값에 대해 시스템이 안정하게 됩니다. 롤 자세 유지 루프의 출력은 아래와 같습니다.

6.3.2 코스 유지 course hold

 횡방향 오토 파일럿 연속 폐루프 설계에서 다음 과정은 바깥 루프인 코스 유지기 설계입니다. $\phi^c$로부터 $\phi$에 대한 내부 루프가 적절하게 조정되면, 주파수 범위가 0에서 $\omega_{n_{\phi}}$까지 $H_{\phi / \phi^c}$ $\aprox$ 1이 됩니다. 이 상태에서 그림 6.6의 블록 다이어그램은 그림 6.11과 같이 바깥 루프 설계 목적으로 블록 다이어그램을 단순화 할 수 있습니다.

 코스 유지기 설계에서 목표는 방위 $\chi$가 입력한 방위 $\chi^c$를 점근적으로 추적하도록 $k_{p_{\chi}}$와 $k_{i_{\chi}}$를 선택하여야 합니다. 이 단순화된 블록다이어그램으로 입력 $\chi^c$와 $d_{\chi}$에 대한 출력 $\chi$의 전달함수는 다음과 같습니다.

여기서 $d_{\chi}$, $\chi^c$는 일정한 상수이며, 최종값 정리로 $\chi$ -> $\chi^c$. 입력 $\chi^c$에 대한 출력 $\chi$의 전달함수는 

 내부 피드백 루프와 함께, 이 피드백 게인 $k_{p_{\chi}}$, $k_{i_{\chi}}$를 계산할수 있는 외부 루프의 고유 주파수와 댐핑비를 골라야 합니다. 그림 6.12는 $H_{\chi}$에 대한 주파수 응답과 스텝 응답을 보여주고 있습니다. 분자의 영점 때문에 $\zeta$를 선택함에 따라  이 전달함수를 바꾸지는 않고, $\zeta$가 클수록 오버슈트가 작아집니다.

 식 (6.10), (6.11)에서 계수를 비교해보면

 $k_{p_{\chi}}$, $k_{i_{\chi}}$에 대해서 풀면

 이 연속 폐루프 설계 과정에서 적절한걸 찾기 위해 내부와 외부 피드백 루프 사이에 다양한 주파수대를 확인해보는게 필요합니다. 적절하게 분리하기 위해 다음 식을 계산하면 됩니다.

 여기서 분할자 separation $W_{\chi}$는 5보다 큰 설계 파라미터로 일반적으로 클 수록 좋으나, $\chi$ 루프에서 느린 응답($\omega_{n_{\chi} 보다 작은}$과 $\phi$ 루프에서 빠른 응답($\omega_{n_{\phi}}$보다 큰)의 분할 주파수가 필요하게 됩니다. 빠른 응답을 받으려면 엑추에이터에 더 큰 비용이 필요하며, 엑추에이터의 물리적인 제한으로 가능하지 않을 수 도 있습니다.

 코스 유지 루프의 출력은 아래와 같습니다.

6.3.3 사이드 슬립 유지 sideslip hold

 비행체는 러더를 장착하고 있는데, 이 러더로 사이드 슬립 각을 0($\beta$ = 0)으로 유지시킬수 있습니다. 이 사이드 슬립 유지 루프는 그림 6.13과 같은데 $\beta^c$로부터 $\beta$에 대한 전달함수는 다음과 같습니다.

 여기서 DC 게인은 1일때 폐루프 극점의 분모가 아래와 같으면

계수를 다음과 같이 정리할 수 있습니다.

 사이드 슬립 최대 오차를 $e_{\beta}^{max}$, 가능한 최대 러더 접힘을 $\deta_{r}^{max}$라고 할 때 6.2장 내용을 따르면

 원하는 댐핑값인 $\zeta_{\beta}$을 주면, 식 (6.14), (6.15)를 풀수 있는데

사이드 슬립 유지 루프의 출력은 다음과 같이 됩니다.

6.4 종방향 오토파일럿 Longitudinal Autopilot

 종방향 오토파일럿은 대기속도가 종방향 동역학에 큰 역활을해서 횡방향 오토파일럿보다 더 복잡합니다. 종방향 오토파일럿 설계에서 목표는 엑추에이터로 스로틀과 엑티페이터를 제어하여 고도와 대기속도를 제어해야합니다. 고도와 대기속도 제어에는 고도 오차가 사용되며 이는 그림 6.14에서 나타납니다.

 이륙 영역 take-off zoned에서는 풀 스로스트 명령이 입력되고 피치 자세는 엘리베이터에 의한 고정 피치 각 $\theta^c$로 제어 됩니다. 상승 영역 climb zone에서 목표는 현제 대기상태에서 상승률을 최대로 해야하며, 이 상승률을 최대로 하기 위해, 풀 스로틀 명령가 피치각을 재어하여 대기속도가 제어됩니다. 만약 대기 속도가 일정 값 이상 넘어가면 비행체가 피치업 하게되어 상승률이 증가하고, 대기속도가 줄어들게 됩니다.

 비슷하게 대기속도가 일정 값보다 줄어들면, 피치가 내려가고, 대기속도는 증가하며 상승 변화율도 감소하게 됩니다. 피치 고도를 이용해 효율적으로 대기속도를 제어하면 스톨 상태를 피할 수 있습니다. 하지만 이륙 직후에는 피치 자세로 대기속도를 제어하지 않고, 비행기가 이륙하고 나서 대기속도를 증가하여 비행체가 땅을 향해서 피치 다운한 뒤에 피치 자세를 제어합니다.

 하강 영역 descend zone은 상승 영영과 스로틀 커멘드가 0인 점을 제외하면 비슷합니다. 스톨 현상 역시 피치각으로 대기속도를 제어해서 피하며, 그렇게 해서 하강 변화율을 최대로 합니다. 고도 유지 영역 altitude hold zone에선 대기속도는 스로틀을 조절하여 대기속도를 제어하며, 고도는 피치 자세 명령으로 제어됩니다.

 그림 6.14와 같은 종방향 오토파일럿을 설계하기위해 다음의 피드백 루프가 필요한데, 첫번쨰로 피치 자세 유지 엘리베이터, 두번째로 스로틀을 사용한 대기속도 유지, 3번째는 피치 자세를 이용한 대기 속도 유지, 피치 자세를 이용한 고도 유지 등으로 이러한 루프들의 설계들을 다루겠습니다. 마지막으로 종방향 오토파일럿을 6.4.5에서 완성하겠습니다.

6.4.1 피치 자세 유지 pitch attitude hold

 피치 자세 유지 루프는 롤 자세 유지 루프와 비슷한데 그림 6.15를보면 $\theta^c$에서 $\theta$에 대해 다음과 같이 전달함수가 주어지는데 이경우 DC 게인이 1이 되지 않습니다.

표준 2차 전달함수에서 응답이 주어지면

분모 계수를 통해 다음을 구할 수 있고

 입력 오차가 최대가 될때 포화 상태를 피하기 위해 비례 제어를 설정한다면, 다음의 식을 구할수 있으며 이 때 $a_{\theta_3}$의 부호는 $C_{m_{\tdelta_e}}$를 기반으로 하며 음수가 됩니다.

 안정성을 확보하기 위해 $k_{p_{\theta}}$, $a_{\theta_3}$은 같은 부호여야 하며 식 (6.19)로부터 피치 루프 주파수를 다음과 같이 계산할수 있으며

식 (6.20)을 $k_d{\delta}$에 대하여 풀면

 정리하자면 엑추에이터 포화도 제한$\delta_{e}^{max}$과 최대 피치 오차 $e_{\theta}^{max}$를 알면 비례 게인 $k_{p_{\theta}}$와 피치 루프의 주파수를 구할수 있습니다. 원하는 댐핑비 $\zeta_{\theta}$를 정함으로서 미분 게인 값 $k_{d_{\theta}}$를 고정 시킬수 있게 됩니다.

 내부 루프 전달함수의 DC게인은 $k_{p_{\theta}}$ -> $infty$가 되며, DC 게인은 다음과 같이되는데 이 게인은 보통 1보다 작은 값이 됩니다.

 모든 주파수 대역에서 내부 루프의 게인을 나타내기 위해 바깥 루프 설계는 DC게인을 사용할것입니다. 내부 루프에서 단위 DC게인으로 하기 위해 적분 요소가 사용될수도 있습니다. 적분기 추가시 내부 루프의 대역폭이 매우 제한될 수 있습니다. 이런 이유로 피치 루프 상에서 적분 제어기를 사용하지 않았습니다.

 그래서 이런 이유로 설계 프로젝트에서 실제 피치각은 명령 피치각에 도달하지 못하게 됩니다. 이는 바깥 루프 설계에서 고려해야 됩니다. 피치 자세 유지 루프의 출력은 다음과 같게 됩니다.

6.4.2 피치 명령을 사용한 고도 유지 

 고도 유지 오토파일럿은 그림 6.16처럼 피치 자세 유지 오토파일럿을 내부루프로 사용하는 연속 폐루프 방식을 사용하며

설계한 피치 루프 함수와 고도 유지 루프는 그림 6.17의 블록 다이어그램으로 추정할수 있게 됩니다.

라플라스 영역에서

폐루프 전달함수는 비행체 파라미터에 독립이고 대기속도에만 의존하게 됩니다. $k_{p_{h}}$, $k_{i_{h}}$는 피치 고도 루프의 주파수가 피치 자세 유지 루프의 주파수보다 작도록 정해야 합니다.

 비슷하게 코스 루프에서 주파수 분할 $W_h$는 아래와 같으며 분할 주파수 $W_h$는 5~16사이의 값을 사용하게 됩니다. 

 고도 유지 루프를 표준 2차 전달함수 형태로 정리한다면

 분모 계수를 정리하면 다음을 구할 수 있습니다.

 $k_{i_h}$, $k_{p_h}$에 대해서 풀면

 댐핑비 $\zeta_h$와 주파수 분할 값 $W_h$를 정해서 $k_{p_h}$, $k_{i_h}$를 정할수 있게 됩니다.

 이 피치를 이용한 고도유지루프의 출력은 아래와 같이 정리할수 있습니다.

6.4.3 피치 입력을 이용한 대기속도 유지

 피치각을 이용한 대기속도 모델은 그림 5.7과 같습니다. 요란 제거를 위해 PI 제어기가 필요한데, 이 블록 다이어그램은 그림 6.18이 됩니다.

 이를 라플라스 영역에서 정리하면

 이때, DC 게인은 1과 같고, 스탭 요란이 제거도비니다. 일정한 대기속도를 유지하기위해, 피치각은 받음각이 0이 아닌 상태로 제어되어야 하며, 적분기가 적절한 받음각을 제어합니다.

 게인 $k_{p v_2}$, $k_{i v_{2}}$는 피치 입력에 대한 대기속도 루프 주파수는 피치 고도 유지 루프의 주파수보다 작아야 합니다. 

여기서 분할 주파수 $W_{v_2}$는 설계 파라미터로 이전에 봤던것과 같은 역활을 합니다. 피드벡 게인은 식 (6.26)의 분모 계수를 2차 표준 전달함수에 대응 시켜서 구할수 잇으며, 사용할 고유 주파수와 댐핑비 $\omega_{n v_2}^{2}$, $\zeta_{v_2}$ 다음과 같이 매칭시키고

제어 게인에 대해 정리할 수 있습니다.

 분할 주파수와 댐핑비 $\omega_{n v_2}^{2}$, $\zeta_{v_2}$를 설정하여 제어 게인  $k_{p v_2}$, $k_{i v_{2}}$을 고정시킬수가 있게 됩니다. 피치에 대한 대기속도 유지 루프의 출력은 아래처럼 정리하게 됩니다.

6.4.4 스로틀을 이용한 대기속도 유지

 스로틀을 입력으로하는 대기속도 동역학식은 그림 5.7에서 보여주는데 이에 대한 제어루프 시스템은 그림 6.19와 같습니다. 우리가 비례 제어기를 사용하면

 여기서 DC 게인은 1이 아니고 스탭 요란이 제거되지 않습니다.

하지만 비례 적분 제어기를 사용하면

 DC 게인이 1이되고 스탭 요란이 제거딥니다. $a_{v_1}$, $a_{v_2}$를 안다면, $k_{p_v}$, $k_{i_v}$는 이전에 했던 방식으로 구할수 있습니다. 폐루프 전달함수의 분모 계수와 표준 2차 전달함수의 계수를 같다고 놓고 정리하면

이 표현식을 정리하여 제어 게인을 구할수 있습니다.

이 루프의 설계 파라미터는 댐핑 계수와 고유 주파수 $\zeta_v$, $\omega_{n_v}$으로, $\bar{V_{a}^{c}}$ = $V_{a}^{c}$ - $V_{a}^{*}$와 $\bar{V_a}$ = $V_a$ - $V_a^*$는 그림 6.19에서 에러 신호로 아래와 같으며

 그러므로 그림 6.19의 제어 루프는 트림 속도 $V_a^*$를 모르고도 구현할 수 있습니다. 만약  스로틀 트림 값 $\delta_t^*$을 안다면 스로틀 제어 입력은 아래의 식이 됩니다.

 하지만 $\delta_t^*$를 정확하게 모르는 경우 $\delta_t^*$에서에러가스탭요란으로들어갈수있고, 적분기로 이 요란을 제거합니다. 스로틀을 이용한 대기속도 유지 루프의 출력은 아래와 같습니다.

6.4.5 고도 제어 상태 머신 altitude control state machine

 종방향 오토파일럿은 $i^b$-$k^b$ 평면에서의 종방향 동작 제어(피치각, 고도, 대기속도)를 다룹니다. 이에 대해서 4가지 서로다른 오토파일럿 모드 (1) 피치 자세 유지, (2) 피치 입력 고도 유지, (3) 피치 입력 대기속도 유지, (4) 스로틀 입력 대기속도 유지 들을 설명하였습니다. 이 종방향 제어 모드를 합쳐서 그림 6.20의 종방향 제어 상태 머신을 만들수 있씁니다.

 상승 영역에서 스로틀은 최대 값($\delta_t$ = 1)이 되고,피치 입력에 대한 대기속도 유지 모드가 대기속도 제어에 사용되어 스톨 현상을 피하도록 만들어줍니다. 이는 비행체가 설정한 고도까지 최대로 올라가기 때문입니다.

 비슷하게 하강 영역에서는 스로틀이 최소 값 ($\delta_t$ = 0)이 되고, 피치 입력에 대한 대기속도 유지 모드는 대기속도를 제어하는데 사용됩니다. 여기서 MAV는 유지해야할 고도 영역까지 일정한 속도로 하강하는데, 그 고도 영역에서 스로틀 입력 대기속도 모드가 $V_a^c$ 주위로 대기속도를 유지시키고, 피치 입력 고도 유지 모드는 $h^c$ 부근에서 고도를 유지시키는데 사용됩니다. 피치 자세 제어 루프는 이 4영역 모든 곳에서 사용하게 됩니다.

 오토파일럿이란 비행체를 조종사 없이 안내하는 시스템을 의미합니다. 유인 비행체에서 오토파일럿은 단순한 단일 축의 윙레벨 오토파일럿에서 다양한 비행 상태(이륙, 상승, 레밸 비행, 하강, 접근, 착륙)동안  고도, 경도, 위도 같은 위치와 롤, 피치, 요와 같은 자세를 제어하는 복잡한 완전 비행 제어 시스템도 있습니다.

 MAV에서는 모든 비행 단계들에서 비행체 제어를 오토파일럿이 해야합니다. 일부 제어 기능을 지상국에서 할수도 있지만 오토파일럿의 대부분 제어 시스템은 MAV 내부에 있습니다.

 이번 장에서는 센서와 MAV 내부에서 계산 가능하도록 적합한 오토파일럿 설계법을 살펴보겠습니다. 여기서 횡방향과 종방향 오토파일럿을 설계하기 위해서 연속 폐루프 succesive loop closure라고 부르는 방법을 사용할건데, 이는 6.1에서 다루어 보겠습니다. 

 비행체의 양력 면은 점위가 제한되므로 액추에이터 포화도 actuator saturation와 거기에서의 성능 제한을 6.2에서 살펴보겠습니다. 횡방향과 종방향에 대한 오토파일럿 설계법은 6.3장과 6.4장에서 다루어 보고, 6.5에서 이산 시간에 대한 비례-적분-미분 피드벡 제어 법칙을 따르는 제어기에 대해 살펴보면서 마치겠습니다.

6.1 연속 폐루프 Successive Loop Closure

 오토파일럿 설계에서 주요 목표는 관성 위치($p_n$, $p_e$, h)와 자세($\phi$, $\theta$, $\chi$)를 제어하는것입니다. 대다수의 비행 제어기에선, 동역학식을 분리하여 설계한 오토파일럿은 좋은 성능을 보입니다. 종방향 동역학(전진 속도, 피칭, 상승, 하강 운동)과 횡방향 동역학(롤링, 요잉 모션)을 나누어 다루어 보겠습니다. 이를 통하여 오토파일럿 설계를 단순화 시키며, 순차 폐루프라 부르는 오토파일럿 설계 방법을 사용할 수 있게 됩니다.

 연속폐루프의 기본 개념은 하나의 복잡한 제어 시스템을 설계하기 보다는, 여러개의 단순한 피드백 폐루프를 개루픞 플랜트 주변에 연속적으로 연결한 것이 됩니다. 

 그림으로 살펴보면 그림 6.1의 개루프 시스템을 다뤄보겠습니다. 개루프 동역학식은 세개의 전달함수를 직렬로 곱하여 구하는데 P(s) = $P_1$(s) $P_2$(s) $P_3$(s)이됩니다. 각각의 전달함수는 출력으로 $y_1$, $y_2$, $y_3$이 나오며 이를 측정하여 피드벡에서 사용됩니다. 여기서  $P_1$(s), $P_2$(s), $P_3$(s) 전달함수 각각은 1, 2차로 상대적으로 저차수가 됩니다.

 이 경우 우리가 제어에서 관심가져야 할 것은 출력 $y_3$이 됩니다. $y_3$ 하나만을 궤환시키는 대신 그림 6.2처럼 $y_1$, $y_2$, $y_3$을 연속적으로 피드백을 시키겠습니다. 보상기 $C_1$(s), $C_2$(s), $C_3$(s)를 설계할 건데 설계 과정의 필수 조건은 내부 루프가 가장 큰 대역폭을 가지고, 각각의 연속 루프 대역폭 요소는 주파수대가 5~10배 정도 작아야 합니다.

 그림 6.2의 내부 루프를 살펴보면 폐루프 설계 목표는 $r_1$로부터 $y_1$을 출력하는 대역폭이 $\omega{BW1}$인 폐루프 시스템을 설계하고자 합니다. 

 폐루프 전달함수 $y_1$(s) / $r_1$ (s)는 이득을 1로 설계할수 있는데 그림 6.3와 같습니다. 이 내부 전달함수의 이득을 1로 설계하면, 두번째 루프는 플랜트 전달함수 $P_2$(s)와 보상기 $C_2$(s)이므로 단순화 시킬수 있습니다. 연속 루프를 닫는데 있어 중요한 과정은 다음 루프의 대역폭을 이전 루프것보다 5 ~ 10배 정도 작게 설계하여야 합니다. 우리의 경우 $\omega_{BW2}$ < $\frac{1} {s}$면 됩니다.

  두 개의 내부 루프를 $y_2$(s) / $r_2$(s) $\approx$ 1이 되도록 설계하면, $r_2$(s)에 대한 $y_2$(s)의 전달함수는  그림 6.4처럼 가장 바깥 루프에 대한 게인 1로 바꿀수 있습니다.

 외부 루프의 대역폭 제한이 있으므로 $\omega_{BW3}$ < $\frac{1} {s^2}$ $\omega_{BW2}$가 됩니다. 각각의 플렌트 모델 $P_1$(s), $P_2$(s), $P_3$(s)는 1 또는 2차이므로 기존의 PID나 뒤섬 보상기가 효율적입니다. 루트 로커스나 루프 형태 같은 전달함수 기반 방법을 주로 사용이 됩니다.

 이후 장에서 횡방향과 종방향 오토파일럿 설계 방법에 다루겠습니다. 5.4장에서 횡방향/종방향 동역학 모델링하는 전달함수를 개발하고 오토파일럿 설계에 사용하겠습니다.

6.2 제한 포화도와 성능 saturation constraint and performance

 연속 폐루프 디자인 과정에서 시스템의 성능은 내부 루프의 성능에 따라 제한이 됩니다. 가장 안쪽의 루프 성능은 제한 포화도로 제한이 될수 있습니다.

 예를 들어 횡방향 오토파일럿 설계시 에일러론은 접을수 있는 각에 물리적으로 제한이 될수 있는데 이는 비행체의 롤 변화율이 제한됨을 의미합니다. 여기서 목표는 내부 루프 대역폭을 포화도 제한을 위반하지 않도록 가능한 크게 설계하는것이고, 바깥 루프를 연속 루프의 대역폭에 맞게 설계하는것입니다.

 이번 장에서 간단하게 플랜트와 제어기 전달함수, 액추에이터 제한 포화도에 대한 지식들이 가장 안쪽 루프의 성능 스펙을 구하는대 사용하는지 알아보겠습니다. 이 과정을 2차 시스템을 사용하여 설명하겠습니다.

 그림 6.5같은 출력 오차를 비례 피드백하고, 출력을 미분 피드백하는 2차 시스템이 주어질때, 이 폐루프 전달함수는 아래와 같고

 이 폐루프 시스템의 극점이 제어기 게인 $k_p$, $k_d$에 의해 정해지는것을 알수 있습니다. 액추에이터 힘 u는 u = $k_p$ e - $k_d$ $\dot{y}$로 나타낼수 있는데, $\dot{y}$는 0이거나 작을 때 엑추에이터 입력 u의 크기는 제어기 오차 e와 제어기 게인 $k_p$로 조정할 수 있습니다.

 이 시스템이 안정하다면 스템 입력에 대한 가장 큰 제어기 입력 응답은 $u^{max}$ = $k_p$ $e^{max}$에서 스텝이 들어간 직후에 발생할 것입니다. 이 내용을 다시 정리하면 비례제어기 계인을 최대 기대 출력 오차와 엑추에이터의 포화도 제한으로 구할수 있는데 식은 다음과 같습니다.

 여기서 $u^{max}$는 시스템이 가능한 최대 제어 입력이고 $e^{max}$는 스텝 입력에 대한 스텝 오차를 의미합니다.

 영점이 없는 표준 2차 전달함수는 다음과 같은 표준 형태로 정의되는데 $y^c$는 제어 입력이고, $\zeta$는 댐핑비, $\omega_n$는 고유진동수를 의미합니다.

 여기서 0 <= $\zeta$ <= 1 이면, 이 시스템은 과소 감쇄 under damped이며, 극점은 복소수로 다음과 같습니다.

 식 (6.1)에서 폐루프 시스템 전달함수의 분모 다항식 계수들을 식 (6.3)에서 표준 2차 전달함수를 엑추에이터의 포화도 제한을 고려하여 비교하면, 사용가능한 폐루프 대역폭에 대한 구할수 있습니다. 

$s^0$ 항의 계수를 같다고 한다면 다음과 같이 정리할수 있는데

 이는 폐루프 시스템 대역폭의 상한선이 되며 엑추에이터의 포화도가 이 값이 되어서는 안됩니다. 6.3.1, 6.4.1장에서 이를 이용하여 롤과 피치 루프의 대역폭을 설정하는데 사용해보겠습니다.

5.5 선형 상태공간 모델

 이번 장에서는 트림 조건에서의 식 (5.1)-(5.12)를 선형화 한 것으로 종방향과 횡방향에 대한 상태공간 모델을 구해보겠습니다. 5.5.1에서 일반적인 선형화 기술들을 살펴보고, 5.5.2에선 횡방향에 대한 상태 공간 방정식, 5.5.3에선 종방향에대한 상태공간 방정식을 살펴보겠습니다. 마지막으로 5.6에서 short-period mode, phugoid mode, dutch-roll mode, spiral-divergence 모드 등 차수 감수 모드 reduced-order mode를 살펴보겠습니다.

5.5.1 선형화

 다음과 같은 비선형 방정식이 주어 질 때 x $\in$ $\mathbb{R}^n$는 상태이며,

 u $\in$ $\mathbb{R}^m$ 제어 벡터가 됩니다. 식 5.3에서 설명한 방법으로 트림 입력 $u^{*}$과 상태 $x^*$은 다음의 관계를 가집니다.

$\bar{x}$ = x - $x^*$로 한다면, 아래의 식을 구할 수 있습니다.

 트림 상태에 대한 1차 테일러 급수 확장을 하면 다음과 같이 정리하게 됩니다.

동역학 선형화는 트림조건에 대한 $\frac{\vartheta f} {\vartheta x}$,  $\frac{\vartheta f} {\vartheta u}$를 찾으면 결정할 수 있습니다.

5.5.2 횡방향 상태공간 방정식

 횡방향 상태 공간 방정식을 구하려면 상태들은 다음과 같이 주어집니다.

입력 벡터는 다음과 같이 정의됩니다.

방정식 (5.5), (5.10), (5.12), (5.7) 그리고 (5.9)를 $x_lat$와 $u_lat$을 이용하여 정리하면 아래와 같습니다.

바람이 없는 상태라면

식 (5.38) ~ (5.42)의 자코비안을 구하면 아래와 같습니다.

 이 미분들을 구해서, 선형화된 상태 공간을 구할 수 있게 됩니다.

이 상태 공간에 대한 계수는 아래의 테이블 5.1이 됩니다.

표 5.1 횡방향 상태공간 계수

횡방향	공식
$Y_v$
$Y_p$
$Y_r$
$Y_{\delta_a}$
$Y_{\delta_r}$
$L_v$
$L_p$
$L_r$
$L_{\delta_a}$
$L_{\delta_r}$
$N_v$
$N_p$
$N_r$
$N_{\delta_a}$
$N_{\delta_r}$

횡방향에 대한 상태공간 식은 $\bar{v}$ 대신 $\bar{\beta}$에 대해서 정리할 수 있는데, 식 (2.7)을

$\beta$ = $\beta ^*$을 대입하여

다음과 같이 정리할 수 있습니다.

$\bar{v}$ 대신 $\bar{\beta}$로 구한 상태 공간 방정식을 아래와 같이 정리할 수 있습니다.

5.5.3 종방향 상태공간 방정식

 종방향 상태공간 방정식에서 상태 값들은 아래와 같고,

입력 벡터는 다음과 같이 정의 됩니다.

식 (5.4), (5.6), (5.11), (5.8), (5.3)을 $x_lon$, $u_lon$의 요소로 구하면 다음과 같이 정리 할수있습니다.

 횡방향 상태($\phi$ = p = r = $\beta$ = v = 0)들과 바람 속도가 0이라고 가정한다면, 

식 (2.7)로부터 아래와 같이 구할 수 있습니다.

식 (5.45)-(5.49)의 자코비안을 구하면

여기서

v =0 인 경우 식 (2.8)을 이용해서 미분 계수를 계산하고 선형화된 상태 공간을 아래와 같이 구할 수 있습니다.

위 식에 대한 계수들은 표 5.2에서 제공하겠습니다.

종방향 상태공간 식은 $\bar{w}$ 대신 $\bar{\alpha}$에 대해서 구할수 있는데, 식 (2.7)로

$\beta$ = 0이라고 할때, $\alpha$ = $\alpha^*$에 대해서 선형화하면 다음 식을 구할 수 있습니다.

이를 정리하면

표 5.2 종방향 상태 공간 모델 계수

종방향	공식
$X_u$
$X_w$
$X_q$
$X_{\delta_e}$
$X_{\delta_t}$
$Z_u$
$Z_w$
$Z_q$
$Z_{\delta_e}$
$M_u$
$M_w$
$M_q$
$M_{\delta_e}$

$\bar{w}$ 대신 $\bar{\alpha}$에 대한 상태공간 방정식을 구할 수 있습니다.

5.6 차수 감소 모드

 비행 동역학 제어에서는 여러가지 개루프 비행 동역학 모드들을 정의하게 됩니다. 이 모드들로 short-period mode와 phugoid mode, rolling mode, spiral-divergence mode, dutch-roll mode 등이 있습니다. 이번 장에서는 각 모드에 대해 간단하게 설명하고, 어떻게 이 모드와 관련된 고유 값들을 근사시킬지 살펴보겠습니다.

Short-period mode

 만약 고도와 추력 입력이 상수값이라면, 식 (5.51)의 종방향 상태공간 모델을 아래처럼 간단하게 구할 수 있습니다.

 우리가 상태 행렬의 고유값을 구한다면 빠르게 감쇄되는 모드와 느리게 감쇄되는 모드를 찾을수 있는데, 빠른 모드를 short period 모드라 하고, 느리게 감쇄되는 모드를 phugoid mode라 부릅니다.

 short-period 모드에서 u를 상수라고 보면 식 (5.52)의 상태공간 식을 $\bar{q}$ = $\dot{\bar{\theta}}$로 대치하여 다음과 같이 정리할 수 있고,

이 식을 라플라스 변환을 적용하면 

이를 정리하면

레벨 비행 level flight ($theta^*$ = 0)에서 선형화를 하면 특성 방정식은

short-period 모드의 극점은 다음과 같이 추정하여 구할 수 있습니다.

Phugoid mode

 $\alpha$가 상수라고 가정하고, $\alpha$ = $\alpha^*$이면 식 (5.52)는 다음과 같이 됩니다.

이를 라플라스 변환을 적용하면

다시 $\theta^*$ = 0으로 가정하면 다음의 특성 방정식을 얻을수 있꼬

phugoid mode의 극점은 다음과 같이 추정하여 구할수있다.

Roll mode

 해딩에 대한 동역학을 무시하고, 상수 피치각으로 가정하면 식 (5.44)는 다음과 같다.

$\bar{p}$에 대한 동역학 식을 식 (5.53)으로 구할수 있으며

롤 모드를 $\bar{\beta}$ = $\bar{r}$ = $\bar{\delta_r}$ = 0일때 구할수 있습니다.

전달함수는 다음과 같습니다.

롤 모드의 고유값을 추정은 아래와 같이 나타납니다..

Spiral-divergence mode

 spiral-divergence 모드는 $\dot{\bar{p}}$ = $\bar{p}$ = 0이고 러더 입력을 무시할수 있다고 가정할때로 식 (5.53)에서 2,3차식으로부터 구할 수 있습니다.

 식 (5.54)를 $\bar{\beta}$에 대해서 풀고, 식 (5.55)에 대입하면

주파수 영역에서 다음과 같이 정리됩니다.

이로부터 spiral mode의 극점을 구하면

이 극점은 보통 복소 평면의 우측에 위치하여 불안정한 모드가 됩니다.

Dutch-roll mode

 더치 롤 모드에서는 롤링 동작을 무시하고, 사이드 슬립과 요에 집중해야 합니다. 식 (5.53)으로

이에 대한 특성 방정식은

더치 롤 모드의 극점은 

 3,4장에서 살펴봤지만 비행체의 운동 방정식은 12개의 비선형, 1차, 동조된, 상미분 방정식의 형태로 복잡하게 되어있습니다. 이런 복잡함 때문에 제어기를 설계하기가 어려우므로 더 직관적인 방법이 필요합니다. 이번 장에서는 운동방정식을 제어기 설계에 더 적합하도록 저차수 reduced-order 전달 함수와 상태 공간 모델로 선형화하겠습니다.

 저수준 오토파일럿 폐루프는 이런 선형 모델을 기반으로 하며, 특정한 상태의 동역학적 특성을 추정하는데 사용합니다. 이번 장의 목표는 6장에서 사용할 선형 모델을 설계하겠습니다.

 고정익 비행체의 동역학적 특성은 대기 속도, 피치각, 고도로 이루어진 종방향 운동과 롤과 해딩각으로 이루어진 횡방향 동작으로 나누어 볼수 있습니다. 종방향과 횡방향은 같이 동조되기는 하지만 요란을 줄이는 제어 알고리즘으로 영향들을 완화할수 있습니다. 이번 장에서는 기존의 방식을 살펴보고 횡방향과 종방향 운동으로 나눠서 살펴보겠습니다.

 이번 장에서 설명하는 많은 선형 모델들은 평형 상태 equilibrium condition로 가정합니다. 비행 통역학에서 힘과 모멘트 평형을 트림 trim이라고 하며 5.3장에서 살펴보겠습니다. 횡방향과 종방향 동역학 식을 5.4장에서 구해보고 상태 공간 모델을 5.5장에서 살펴보겠습니다.

5.1 비선형 운동방정식 요약

 항공역학적 힘과 모멘트는 선형화 범위나 커플링 정도에 따라 다양한 모델들이 존재 할 수 있습니다. 이번 장에서는 6 자유도와 선형에 가까운 quasi-linear, 12 상태 운동방정식, 추진 모델 등 정리하겠습니다.양력과 항력 계수가 받음각에 대해 비선형이고, 프로펠러 추진 또한 스로틀 입력에 대해 비선형이므로 선형으로 나타내어야 합니다. 양력과 항력에 대해 주로 사용하는 선형 모델을 구할 것이고 4장에서 구한 모델들을 다음과 같이 정리 할수 있습니다.

 h = $-P_d$는 고도이고,  $\gamma$는 식 (3.13)에서 정의한 관성 파라미터가 됩니다.

 4장에서 본 x, z 방향 항공역학적 힘계수는 받음각의 비선형 함수로 정리하면 아래와 같습니다.

 항력에 대해서는 양력의 비선형 함수로 설계하는 것이 일반적입니다. 여기서 e는 오즈왈드 값이고, AR은 날개의 종횡비가 됩니다.

 저 받음각 비행 상태 설계를 한다면, 양력과 항력 계수에 대한 선형 모델을 사용할수 있습니다.

 이번 장에서는 스로틀과 비행 제어면(에일러론, 엘리베이터, 러더)를 입력으로 하는 동역학적 특성을 정리 할 것이고, 이 방정식은 각 장의 실습에서 핵심 요소로 사용됩니다.

 이 방정식을 대체하는 방법으로 쿼터니온을 사용할 수도 있습니다. 쿼터니언 기반 방정식은 짐벌락 문제를 해결하였으며 오일러 각 기반 방정식보다 효율적으로 계싼하는 장점을 가지고 있습니다. 그래서 고정밀 시뮬레이션에서 쿼터니언을 이용한 형태의 운동방정식을 사용하기도 합니다. 

 쿼터니언 표현 방법은 물리적으로 이해하기는 힘들어 오일러각 표현방식이 이번 장의 선형 모델 개발시에 주로 사용할 것입니다. 짐벌락 문제를 제거하는 방법은 차후에 다루겠습니다.

5.2 정상 선회 Coordinate Turn

 식 (5.9)의 방정식을 보면, 해딩 변화율은 피치/요/롤 변화율과 관련되어 있습니다. 각각의 상태는 상미분 방정식 형태로 다루어 지는데 물리적으로 롤이나 비행체의 경사 각에 따라 해딩 변화율을 알수 있을 것이고 이 단순한 관계로 선형 전달함수를 개발할 것입니다.

 정산 선회 상태가 이러한 관계를 알려주는데, 이 상태에서 승객들은 편안함을 느낄수 있습니다. 정상 서회를 하는 동안 측면으로 작용하는 가속이 존재하지 않게 되는데 비행체는 측면으로 미끄러지기 보다는 꺽이면서 비행하게 됩니다. 해석학적 관점에서 보면 정상 선회를 이용해서 해딩각 변화율과 경사각 사이 관계를 단순화 시킬수 있습니다.

 이 정상 선회 동안 경사각 $\phi$는 비행체 옆면으로 순 힘이 존재하지 않게 되는데 이 때 자유 물체도를 5.1에서 볼수 있으며, 비행체에 작용하는 원심력은 양력의 수평 요소와 같은 크기로 반대 방향으로 작용하게 됩니다. 수평 방향의 힘을 합하면 다음과 같습니다.

 위 식에서 $F_list$는 양력, $\gamma$는 비행 경로각 flight path angle, $V_g$는 대지 속도 ground speed, $\chi$는 방위 각 course angle이 됩니다.

 원심력은 관성 좌표계 $k^i$  축에 대한 방위각 변화율 $\dot_{\chi}$과 대기 속도의 수평 요소인 $V_a$cos $\gamma$를 이용해서 구할 수 있습니다. 비슷하게 양력의 수직 요소는 $i^b$-$k^b$ 평면에 대한 중력의 사영과 반대 방향으로 동일하게 작용하는데 이는 그림 5.1과 같습니다. 수직 힘 요소들을 합하면 다음과 같이 정리 할 수 있습니다.

 식 (5.13)을 식 (5.14)를 나누고 방위각 변화율 $\dot_{\chi}$에 대해 풀어낸 식은 정상 선회 방정식이 됩니다.

 선회 반지름 turning radius 는 R= $V_g$ cos $\gamma$ / $\dot_{\chi}$로 구할수 있으며, 다음의 식을 얻을 수 있습니다.

 바람이나 사이드 슬립이 없는 경우 $V_a$ = $V_g$이며 $\psi$ = $\chi$이므로 정상 선회에 대해 다음의 표현 식을 구할 수 있습니다.

 이러한 정상 선회 표현들은 비행체의 선회  동역학 표현을 단순화 하는데 사용할 수 있으며, 9.2장에서 더 다루어 보겠습니다. 

5.3 트림 조건 trim conditions

 미분 방정식을 나타내는 다음의 비선형 시스템이 주어진다면, f: $\mathbb{R}^n$ $x$ $\mathbb{R}^m$ -> $\mathbb{R}^n$, $x$는 시스템 상태, u가 입력

이 시스템은 상태 $x^*$와 입력 $u^*$에 대해 평형이라고 할 수 있습니다.

 비행체가 상수의 고도와 정상 비행 steady flight 중일때 이 상태 값들은 평형 상태에 있습니다. 고도 h=-$p_d$, 동체 좌표계 속도 u, v, w, 오일러각 $\phi$, $\theta$, $\psi$, 그리고 각 속도 p,q,r은 모두 상수 값이 됩니다.

 이러한 평형 상태에 있는 비행체를 트림에 있다고 말 할 수 있습니다. 트림 조건은 상태가 상수가 아닌 경우도 포함합니다. 예를 들자면 정상 상승 steady climb 시, $\dot_{h}$는 상수가 되고 h는 선형 적으로 상승하게 됩니다. 역시 선회 각 변화율 $\dot_{\psi}$는 상수이면, $\psi$는 선형적으로 증가하게 됩니다. 더 일반적으로 트림 조건을 나타내자면 다음과 같이 정리 할 수 있겠습니다.

 트림 계산 수행 과정에서 바람을 알수없는 요란으로 다루어야 하는데, 비행체에 작용하는 여향을 알 수 없으므로 바람 속도를 0으로 치고 트림을 찾을 것인데 이때 $V_a$ = $V_g$, $\psi$ = $\chi$, $\gamma$ = $\gamma_{a}$가 됩니다.

 비행체가 다음 새가지 조건을 만족할 때 트림 상태와 입력값들을 계산하는것이 목표 입니다.

 - 상수 속도 $V_a^*$로 비행 중인 상태

-  상수 비행 경로각 $\gamma^*$으로 상승 중인 상태

- 상수 반지름 궤적 $R^*$을 가질때 

 이 새 파라미터 $V_a^*$, $gamma^*$, $R^*$는 트림 계산에서 입력이 되며, $R^*$ >= $R_{min}$으로 가정한다면, $R_{min}$은 최소 선회 반지름이 됩니다.

 일반적인 경우 필요한 트림 값으로, 윙 래밸과 상수 고도값으로 이 경우 $\gamma^*$ = 0, $R^*$ = $\infty$가 됩니다. 다른 흔한 경우로 상수 고도와 반지름으로 이 경우 $\gamma^*$ = 0이 됩니다.

 일반적인 고정익 비행체의 상태들은 다음과 같이 나타내며

 입력 값들은 아래와 같이 주어집니다.

 f(x,u)은 방정식 (5.1)-(5.12)의 우항들로 정의할 수 있습니다. 그러나 식의 우항들은 위치 $p_n$, $p_e$, $p_d$에 대해 독립이므로, 트림 비행은 위치에 대해 독립이 됩니다. 그리고 $\dot{p_n}$, $\dot{p_e}$는 $\psi$에 의존하므로 트림 비행은 해딩각 $\psi$에 독립적이게 됩니다.

 상수  상승 궤도에서 비행체의 속도가 변하지 않을 때 $\dot_{u^*}$ = $\dot_{v^*}$ = $\dot_{w^*}$=0가 됩니다.비슷하게 롤과 피치 각이 일정하면, $\dot_{\phi^*}$= $\dot_{\theta^*}$= $\dot_{p^*}$ = $\dot_{q^*}$ = 0이 됩니다. 선회 속도가 상수인 경우에는 다음과 같이 정리 할 수 있습니다.

 상승 속도가 일정하다면 이 식을 다음과 같이 정리 할 수 있습니다.

 $V_a^*$, $\gamma^*$, $R^*$ 파라미터가 주어지면 $\dot{x^*}$는 아래와 같이 정의 됩니다.

 $x^*$와 $u^*$를 찾는 문제($\dot{p_n^*}$, $\dot{p_e^*}$, $h^*$, $\psi^*$ 제외한)로 비선형 시스템의 방정식을 풀수 있씁니다. 이러한 시스템 방정식을 풀기 위해 다양한 수치 기법들이 있지만 시뮬링크의 trim 명령어로 사용할수 있습니다. 

5.4 전달함수 모델 Transfer Function Models

 횡방향에 대한 전달함수 모델을 5.4.1에서 구할 것인데, 이는 비행체의 수평 방향의 동작을 나타냅니다. 종방향 동역학에 대한 전달함수 모델은 비행체의 수직 방향 동작을 나타내며 5.4.2에서 구하겠습니다.

5.4.1 횡방향 전달함수 lateral transfer functions

 횡방향 동역학에서 관심 변수로 롤 각 $\phi$,  롤 속도 p, 해딩 각 $\psi$, 요 속도 r 이 있습니다. 횡방향 동역학에 영향을 주는 제어면으로 에일러론 $\delta_a$와 러더 $\delta_r$이 있습니다. 러더는 롤 속도 p에 주로 영향주며, 러더는 요 $\psi$를 제어하는대 주로 사용합니다.

롤 각 roll angle

 에일러론 $\delta_a$로부터 롤 각 $\phi$에 대한 전달 함수를 구하기 위해 식 (5.7)을 다시 봅시다.

대부분 비행 상태에서, $\theta$는 작고, $\dot{phi}$에 영향 주는 것은 롤 속도 p가 되므로 다음과 같이 정의할 수 있습니다.

이 요란은 (5.22)의 미분 방정식을 나타내며,

식 (5.10)을 이용하여 다음과 같이 정리 할 수 있는데, $\delta_{phi_2}$는 시스템의 요란을 의미합니다.

 라플라스 영역 으로 정리하면 아래의 식을 구할 수 있습니다.

이 블록다이어 그램은 그림 5.2에서 보여주며 입력은 에일러론 $\delta_a$, 요란은 $d_{\phi_2}$가 됩니다.

방위각 course and heading

 롤 각으로 방위 각 $\chi$도 구할수 있는데, 바람이 없는 정상선회 상태라면 아래의 식이 되며

이 식을 아래와 같이 정리 할 수 있습니다.

라플라스 영역에서 나타내면 다음과 같습니다.

이는 그림 5.3에서 보여주는것 처럼 에일러론으로 횡방향 역학을 제어하는 블록 다이어 그램을 구할 수 있씁니다. 전달함수로 구하기 위해 대기 속도 $V_g$가 필요하며, 바람이 없고,  $V_g$를 대기 속도로 사용하여 구할 수 있습니다. 

 6장에서 비행 결로 제어를 위한 제어기 설계를 할것이며, 경로 각은 gps로 측정 할수도 있지만 식 (5.27)과 같이 경로각 $\chi$에 대한 전달 함수를 구할 수 있씁니다. 이 전달함수는  아래와 같습니다.

사이드 슬립 sideslip

 측면 역학의 두번째요소로 러더 입력에 대한 요 동작인데, 바람이 없는 경우 v = $V_a$ sin $\beta$가 되며, 대기 속도가 일정하면 $\dot{v}$ = ($V_a$ sin $\beta$) $\dot{\beta}$가 됩니다. 그러므로 식 (5.5)로 아래와 같이 정리 할 수 있습니다.

 $\beta$가 충분히 작으면 cos $\beta$ $\approx$ 1 이며 아래와 같이 됩니다.

이를 라플라스 영역에서 구하면 다음과 같습니다.

 이 전달함수는 그림 5.4에서 블록 다이어그램으로 나타내게 됩니다.

종방향 전달함수 longitudinal transfer function

 이번 장에서는 종방향 역학에 대한 전달함수를 구할 건데, 관심 변수로 피치각 $\phi$, 피치 변화율 q, 고도 = -$p_d$, 대기 속도 $V_a$가 있습니다. 종방향 역학에 영향을 주는 제어 신호로 엘리베이터 $\delta_e$, $\delta_t$가 있습니다.

 엘리베이터는 피치각 $\phi$에 직접 영향을 주며 아래에서 보겠지만 피치각은 고도 h와 대기속도 $V_a$를 제어하는데 사용될 수 있씁니다. 대기 속도는 고도를 제어하는데 사용되며, 스로틀은 대기 속도에 영향을 줍니다.

 이번 장에서 구한 전달함수로 6장에서 고도 제어기를 설계하는대 사용될것입니다.

피치각 pitch angle

 엘리베이터 $\delta_e$와 피치각 $\theta$ 사이 관계를 단순화해서 구하면 식 (5.9)로 아래의 식을 얻을 수 있습니다. 이때 $d_{\theta_1}$ = q (cos $\phi$ - 1) - r sin $\phi$이고, $d_{\theta_1}$은 충분히 작습니다.

이를 미분하면 다음과 같고,

식 (5.11)과  $\gamma_r$ = $\gamma$ 가 비행 경로 각일 때, $\theta$ = $\alpha$ + $\gamma_a$ = $\gamma$인 관계를 이용하면 아래의 식을 얻을 수 있습니다.

피치각에 대한 선형 모델을 구하고 라플라스 변환을 하면 다음의 식을 가지게 됩니다.

 이때는 직선 비행으로 r = p = $phi$ = $\gamma$ = 0 이며, 비행체가 $C_{m_0}$ 이되도록 설계합니다. 그러면 $d_{\theta_2}$ = 0이 됩니다. $\dot{\theta}$ = q + $d_{\theta_1}$을 이용하여 그림 5.5의 블록다이어그램을 얻을 수 있는데, 피치 변화율 q를 자이로로 부터 궤한 받을수 있어 쓰기 좋습니다.

고도 Altitude

 대기 속도가 일정한 경우, 피치각은 상승 변화율에 직접적으로 영향을 주므로 피치 앵글로부터 고도에 대한 전달함수를 구할 수 있습니다. 식 (5.3)으로 아래의 식을 구할 수 있습니다.

 v $\approx$ 0, w  $\approx$ 0, u  $\approx$ $V_a$, $\phi$  $\approx$ 0, $\theta$가 작을때, 비행체는 직진 비행을 하며 $d_h$는 0이 됩니다.

 $V_a$가 일정하고, 피치각 $\theta$가 입력될때에 대해 라플라스 영역에서 나타내면 아래와 같고,

 엘리베이터로부터 고도를 구하는 종방향 운동방정식의 블록 다이어그램은 그림 5.6과 같습니다. 대신 피치각이 일정하고, 대기 속도가 빨라진다면, 날개의 양력을 증가시켜 고도를 변화 시킬 수 있습니다.

 이 대기속도로부터 고도에 대한 전달함수를 구하기 위해 피치각 $\theta$를 고정시키고, $V_a$를 입력으로 한다면 다음의 식을 얻을 수 있습니다.

 고도 제어기는 6장에서 다룰예정이며 피치각과 대기 속도를 이용해서 고도를 제어합니다. 대기속도는 스로틀과 피치각으로 조절하게 됩니다. 예를들자면 피치각이 고정되어있고 스로틀로 추력을 증가시키면, 비행체의 대기속도는 증가하게 됩니다. 그러나 스로틀이 고정되고 비행기 머리를 아래로 내리도록 피칭 하면 양력이 감소하여 중력에 의한 가속 영향을 받게 만들어 비행체의 대기속도가 증가하게 됩니다.

대기속도 Airspeed

 종방향 모델을 완성시키려면, 스로틀과 피치각으로부터 대기속도에 대한 전달함수를 구해야 합니다. 그러기 위해 우선 바람 속도를 0으로 가정하여 $V_a$ = $\sqrt{u^2 + v^2 + w^2}$로 다음의 식을 구할수 있고

 식 (2.7)을 이용하면 아래의 식이 됩니다.

 $\beta$ = 0이면, $d_{v1}$ = 0이고 식 (5.4)와 (5.6)을 식 (5.33)에 대입하면 아래의 식을 얻을수 있습니다.

 식 (2.7)과 선형 추정 $C_D$($\alpha$) $\approx$ $C_{D_0}$ + $C_{D_{\alpha}}$ $\alpha$을 이용해서 단순화 시키면 다음의 식을 얻을 수 있습니다.

이 때 $d_{v_2}$ $\approx$ 0이 됩니다.

 대기속도 $V_a$를 다룰때 관심 입력값으로 스로틀 세팅 $\delta_t$와 피치각 $\theta$가 있습니다. 식 (5.34)는 $V_a$와 $\delta_t$

에 대해 비선형이므로, 원하는 전달함수를 구하기 전에 1차 선형화를 해야 합니다. 5.5.1장의 개요를 따라가보면 식 (5.34)을 트림 상태 대기속도와 $V_a$의 편차인 $\bar{V_a}$ = ${V_a}$ - ${V_a^*}$ 로 바꾸고, 트림 상태의 피치각과 $\theta$의 편차인 $\bar{\theta}$ =  $\theta$ - $\theta^*$, 그리고 트림 떄의 스로틀 편차인 $\bar{\delta_t}$ = $\delta_t$ - $\delta_t^*$로 바꾸어서 선형화 할 수 있습니다. 

 식 (5.34)는 윙 레벨과 상수 고도($\gamma^*$ = 0) 트림 조건에 따라 선형화 하면 다음과 같이 구할 수 있습니다

 $d_v$와 $d_{v_{2}}$는 선형화 오차이며, 라플라스 영역에서 아래의 식을 구할수 있습니다.

이에 대한 블록다이어그램은 그림 5.7에서 보여줍니다.

4.2.4 항공역학적 계수

 항공역학적 계수인 $C_{m_{\alpha}}$, $C_{l_{\beta}}$, $C_{n_{\beta}}$, $C_{m_{q}}$, $C_{l_{p}}$, $C_{n_{r}}$은 안정성 미분계수로 이 값들이 비행체의 정적, 동적 안정성을 결정하게 된다.

 정적 안정성 static stability는 일반 비행 상태서 항공역학적인 모멘트를 다루는데, 모멘트가 기존 상태로 돌아가려 한다면 정적으로 안정한 것이 된다. 대부분의 비행체는 정적으로 안정하도록 설계 된다.

$C_{m_{\alpha}}$, $C_{l_{\beta}}$, $C_{n_{\beta}}$는 비행체의 정적 안정성을 결정하며 대기 속도 벡터의 방향 변화에 대한 모멘트 계수 변화량을 의미한다.

 $C_{m_{\alpha}}$은 종방향 정적 안정성 미분 계수로 비행체가 안정하다면 $C_{m_{\alpha}}$는0보다작게된다. 이 경우 비행체가 상승시 받음각이 증가하게 되는데, 비행체가 아래를 향하도록하여 받음각을 안정한 상태로 유지시키게 합니다.

 $C_{l_{\beta}}$는 롤 정적 안정성 계수로 날개의 상반각 dihedral과 관련이 있습니다. 롤에서의 정적 안정성을 나타내는 $C_{l_{\beta}}$는 반드시 음수가 되어야하는데, 사이드 슬립 방향과 반대로 롤 하여 사이드 슬립 각이 0이 되도록 만듭니다.

 $C_{n_{\beta}}$는 요 안정성 미분 계수로 풍향계 안정성 계수 weathercock stability derivative라고도 부르는데, 비행체가 요에 대해 안정적이라면, 풍향계처럼 바람이 오는쪽으로 향하게 됩니다. $C_{n_{\beta}}$ 값은 비행체 꼬리의 설계에 따라 크게 영향을 받는데, 꼬리가 크고 질량의 중심으로부터 떨어질수록, $C_{n_{\beta}}$는 커지게됩니다. 비행체가 요에 대해 안정적이라면 이 값은 양수가 됩니다. 이는 양의 사이드 슬립각에 의해 양의 요 모멘트가 발생한 경우 이 안정성 계수는 대기 속도 벡터의 방향으로 비행체를 요시켜 사이드 슬립각을 0으로 만들게 됩니다.

 동적 안정성은 요란에 대해 비행체의 동적인 반응을 다룹니다. 요란이 비행체에 작용할 때 비행체의 응답이 시간에 따라 감쇄가 된다면 이 비행체는 동적으로 안정적이라고 할 수 있습니다. 비행체를 분석하기 위해 2차 질량-스프링-댐퍼 개념을 사용한다면 안정성 계수인 $C_{m_{\alpha}}$, $C_{l_{\beta}}$, $C_{n_{\beta}}$는 스프링 같은 동작을 하고, $C_{m_{q}}$, $C_{l_{p}}$, $C_{n_{r}}$는 댐퍼 같은 역활을 한다고 볼 수 있습니다.

 5장에서 볼것이지만 비행체의 동적 방정식을 선형화 시에 안정성 계수들은 비행체의 동적 특성을 덜 복잡하게 하기 위해 일정한 값을 사용하여야 합니다.

 $C_{m_{q}}$는 피치 댐퍼 미분 계수, $C_{l_{p}}$는 롤 댐퍼 미분 계수, $C_{n_{r}}$는 요 댐퍼 미분 계수로 각각의 댐퍼 미분 계수들은 운동 방향과 모멘트가 반대로 발생해서 감쇄해야하므로 일반적으로 음수가 됩니다.

 항공역학적인 계수인  $C_{m_{\delta_{e}}}$, $C_{l_{\delta_{a}}}$, $C_{n_{\delta_{er}}$은 제어면의 접힘 정도와 연관되어 있어 주 제어 미분계수 primary control derivative 라고 부릅니다. 이 값들은 제어면을 접으면서 발생하는 모멘트이므로 주요하게 작용합니다. 예를들어 엘리베이터 접힘 $\delta_e$에 따라 피칭 모멘트 m이 발생하게 됩니다.

 $C_{l_{\delta_{r}}}$, $C_{n_{\delta_{a}}}$는 교차 제어 미분 계수로, 제어 면이 접힐때 발생하는 축 밖으로 작용하는 모멘트가 됩니다. 제어 미분 계수를 게인으로 본다면, 제어 계수의 값이 클수록 제어면이 접힘에 따른 모멘트의 크기는 커지게 됩니다.

4.3 추진력과 추진 모멘트

4.3.1 프로펠러 추력

 프로펠러로 발생하는 추력 모델은 베르누이 법칙을 이용하여 프로펠러의 압력차이로 구할 수 있습니다. 베르누이 방정식을 이용해서 프로펠러로 들어오는 총 압력은 다음과 같습니다. $P_0$는 정적 압력이고, $\rho$는 대기 밀도가 됩니다.

 프로펠러 밖 downstream으로 나가는 압력은 다음과 같이 정의 할 수 있는데 여기서 $V_{exit}$는 프로펠러에서 나가는 대기의 속도가 됩니다.

 모터의 순간적인 영향은 무시하고, pwm 명령 $\delta_t$와 프로펠러 각속도는 선형 관계를 가지므로 프로펠러에서 다음 속도의 나가는 바람을 발생시킵니다.

 만약 $S_prop$가 프로펠러가 맞닫는 넓이라고 한다면, 발생하는 추력은 아래와 같이 정리할 수 있습니다.

 대다수의 비행체의 추력은 동체 좌표계 $i^b$축에 따라 작용하므로 질량의 중심에 대해 다른 모멘트를 발생시키지는 않습니다.

4.3.2 프로펠러 토르크

 프로펠러 회전에 따라 공기가 프로펠러를 지나가면서 추력이 기체에 발생함과 동시에 공기의 모멘텀을 만듭니다. 프로펠러 내부 공기에 의해 같거나 반대방향의 힘들이 작용하게 되는데 이 힘들의 영향이 토르크가 되어 기체가 프로펠러의 축을 따라 회전하도록 만듭니다.

 이 모터에 의해 프로펠러에 작용하는 토르크는 같은 방향이나 프로펠러에 의해 모터에 작용하는 토르크는 반대 방향으로 작용하게 됩니다. 프로펠러 회전과 반대 방향인 이 토르크는 프로켈러 각속도의 제곱에 비례하여 다음과 같이 정리 할 수 있습니다.

 여기서 $\Omega$ = $k_{\Omega}$ $\delta_t$ 는 프로펠러 속도이며, $k_{T_{p}}$는 실험에 따라 정해지는 상수가 됩니다. 그러므로 이 추진 시스템의 모멘트는 다음과 같습니다.

 이 프로펠러 토르크의 영향은 상대적으로 적을수 있으나 이를 고려하지 않으면, 프로펠러 토르크가 프로펠러 회전과 반대 방향으로 느린 롤 모션을 발생시킬수 있습니다. 고치는 간단한 방법은 약간의 에일러론 접힘으로 프로펠러 토르크를 상쇄시키는 롤 모멘트를 만들어 내면 됩니다.