무인 비행체 시스템을 배우는데 있어서 동체들이 서로 서로 비교할때 얼마나 다르게 방향을 향하는지 이해하는게 중요합니다. 정확하게 얘기를 하면 기체가 지구를 기준으로 어딜 향하는지 이해하여야 합니다. 또, 카메라 같은 센서가 깇체와 비교할때 어디를 향하고 있는지, 안태나가 신호와 얼마나 향하고 있는지도 알아야 합니다. 이번 장에서는 기체와 센서의 위치와 방향을 나타내는데 사용하는 다양한 좌표계 시스템과 이 좌표계들 간의 변환을 설명하고자 합니다. 서로 다른 여러 좌표계 시스템은 아래의 이유들로 반드시 사용해야 합니다
- 뉴턴의 운동 방정식은 고정된 관성 기준 좌표계 inertial reference frame에서 구하나, 운동은 동체 고정 좌표계 body-fixed frame 에서 나타내어야 합니다.
- 동체에 작용하는 항공역학적인 힘과 토르크는 동체 고정 기준 좌표계 body-fixed reference frame 에서 나타내기가 쉽습니다.
- 가속도계나자이로 같은 센서는 동체 좌표계에 대해서 정보를 측정합니다. 하지만 gps 같은 경우 관성 좌표계에 대해 위치와 대지 속도, 방위각을 측정합니다.
- 대부분의 임무에서는 비행 지점, 궤적 같은 것들이 필요하며 이들은 관성 좌표계에서 표현됩니다. 지도 정보들 또한 관성 좌표계에서 주어집니다.
하나의 좌표계는 회전 rotation과 평행 이동translation 동작으로 다른 좌표계로 변환됩니다. 2.1장에서 회전 행렬과 좌표계 변환에서 사용하는 과정을 보여줄 것이고, 2.2장에서는 소형 비행체에서 사용하는 특정한 좌표계들을 설명하고자 합니다. 2.3장에서는 대기속도 airspeed와 대지속도 ground speed, 바람속도 wind speed와 이들 사이의 관계를 설명하고, 이들을 통해 2.4장에서 바람 삼각형 wind triangle에 대해 상세히 다루고자 합니다. 2.5장에서는 좌표계의 회전과 평행이동에서 백터 미분 표현을 설명하려고 합니다.
회전 행렬
그림 2.1의 두 좌표계를 살펴 봅시다. 벡터 p는 $F^0$ 좌표계에서 $(i^0, j^0, k^0)$로 $F^1$ 좌표계에서는 $(i^1, j^1, k^1)$ 나타낼수 있습니다. $F^0$ 좌표계에서 벡터 $p$는
$p = p_x^0 i^0 + p_y^0 j^0 + p_z^0 k^0$
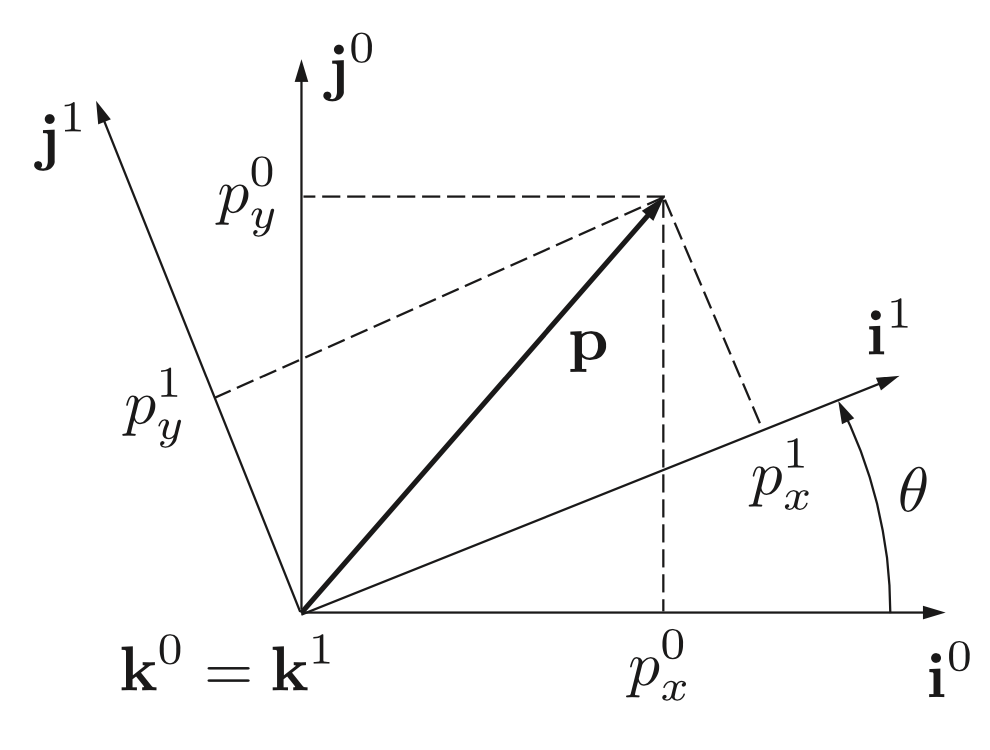
$F^1$ 좌표계에서 벡터 $p$는 아래와 같습니다.
$p = p_x^1 i^1 + p_y^1 j^1 + p_z^1 k^1$
벡터 $(i^0, j^0, k^0)$와 $(i^1, j^1, k^1)$는 서로 직각이 되는 기저 벡터가 됩니다.
두 식이 같다고 하면 다음과 같이 정리 할 수 있게 됩니다.
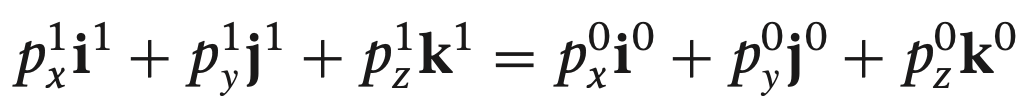
양 쪽을 $i^1, j^1, k^1$로 내적을 구하면, 다음의 행렬이 만들어 집니다.
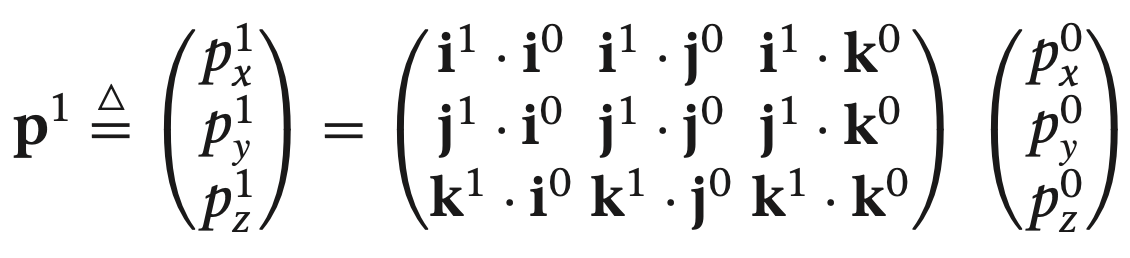
그림 2.1을 정리하여 다음의 식을 구할 수 있습니다.
$ p^1 = R_0^1 p^0 $ (2.1)

$R_0^1$이란 표기는 좌표계 $F^0$에서 $F^1$으로의 회전을 나타내며, 비슷하게 y축에 대한 좌표계의 오른손 회전으로 다음의 식을 구할 수 있습니다.

x축에 대한 오른손 회전 결과는 아래와 같습니다.

행렬 $R_0^1$은 일반적인 정규 직교 행렬로 다음의 성질들을 가지고 있습니다. (det는 행렬의 행렬식)
P.1.. $(R_a^b)^{-1} $ = $(R_a^b)^T $ = $R_b^a$
P.2. $R_b^c R_a^b$ = $R_a^c$
P.3. det($R_a^b$) = 1
식 2.1로부터 벡터 $p$는 변하지 않으며, 새 좌표계 $R^1$는 $F^0$을 각 $\theta$ 만큼 오른손 회전하여 얻을 수 있다. 또한 회전 행렬로 벡터를 회전시킬수도 있다. 그림 2.2는 $F^0$에서 벡터 p를 $k^0$ 축에 대해 각 $\theta$만큼 왼손 회전한 결과를 보여준다.

벡터 p와 q를 $i^0 - j^0$ 평면에서 정의한다면, p와 에 대해 다음과 같이 정리할 수 있다.


식 (2.2)와 (2.3)는 아래와 같이 정리 할수도 있다.

q = $R_0^1$ p
회전 행렬 $R_0^1$는 벡터 p의 각 $\theta$에 대한 왼손 회전으로 같은 좌표계 상에서 새로운 벡터 q를 구한다. q에서 p로 즉 벡터의 오른손 회전은 $(R_0^1)^T$로 구할수 있다.
MAV 좌표계
MAV 동역학을 이해하고 구하려면 여러 좌표계를 이해하여야 하며 여기서 관성 좌표계 inertial frame, 기체 좌표계 vehicle frame, 기체 1 좌표계 vehicle 1 frame, 기체 2 좌표계 vehicle 2 frame, 동체 좌표계 body frame, 안정성 좌표계 stability frame, 바람 좌표계 wind frame에 대해 설명하고자 합니다. 관성 좌표계와 기체 좌표계는 평행이동과 연관되며 나머지 좌표계들은 회전과 관련됩니다. 기체의 상대적인 방향이 각이므로 기체, 기체1, 기체2, 동체 좌표계는 오일러 각으로 유명한 롤, 피치, 요 각을 나타냅니다. 동체/안정성/바람 좌표계 사이 상태적인 회전 각은 받음 각 angle of attack과 사이드 슬립 각 sideslip angle이라 합니다.
관성 좌표계 $F^i$
관성 좌표계는 지정된 위치를 원점으로 하는 지구 고정 좌표계로 그림 2.3에서 단위 벡터 $i^i$는 북쪽을, $j^i$는 동쪽을, $k^i$는 지구 중심 즉 아래를 향합니다. 이 좌표계 시스템은 NED(North East Down) 기준 좌표계라고 부르기도 합니다. 여기서 북쪽을 관성 x 방향, 동쪽을 관성 y 방향, 아래를 관성 z방향이라고 부릅니다.

기체 좌표계 $F^v$
기체 좌표계의 원점인 MAV 질량의 중심이 됩니다. 하지만 $F^v$의 축은 관성 좌표계 $F^i$와 나란합니다. 즉, 단위 벡터 $i^v$는 북, $j^v$는 동, $k^v$는 지구 중심을 향하며 그림 2.4와 같습니다.

기체 1 좌표계 $F^{v1}$
기체 1 좌표계의 원점은 기체 좌표계와 동일하게 비행체 질량의 중심이 됩니다. 하지만 $F^{v1}$은 $k^v$ 축으로 해딩 각(요) $\psi$ 만큼 오른손 양의방향으로 회전하여 구합니다. 추가적인 회전은 없이 $i^{v1}$는 비행체의 코를 가리키며, $j^{v1}$는 기체의 오른쪽 날개, $k^{v1}$는 지구 중심을 향하며 기체 좌표계 1은 그림 2.5와 같습니다.
기체 좌표계 $F^v$에서 기체 1 좌표계 $F^{v1}$로의 변환은 다음과 같이 구합니다.
$p^{v1}$ = $R_{v}^{v1}$($\psi$) $p^{v}$


기체 2 좌표계 $F^{v2)$
기체 2 조표계의 원점은 역시 기체 질량 중심이며 기체 1 좌표계를 $j^{v1)$ 축에 대해 피치각 $\theta$만큼 오른손 회전하여 구합니다. 단위 벡터 $i^{v2)$는 기체의 코를 가리키며, $j^{v2)$는 오른쪽 날개, $k^{v2)$는 배를 향하게되어 그림 2.6과 같습니다.
기체 1 좌표계 $F^{v1)$에서 기체 2좌표계 $F^{v2)$로의 변환은 다음과 같습니다.
$p^{v2)$ = $R_{v1}^{v2}$ ($\theta$) $p^{v1}$


동체 좌표계 $F^{b}$
동체 좌표계는 기체 2 좌표계에서 $i^{v2}$ 축으로 롤 각 $\phi$만큼 오른손 회전을 하여 구합니다.그러므로 원점은 질량의 중심이고, $i^{b}$는 기체의 코, $j^{b}$는 오른쪽 날개, $k^{b}$는 배를 가리키게되며 그림 2.7과 같습니다.
기체 2좌표계 $F^{v2}$에서 $F^{b}$로 변환은 다음과 같습니다.
$p^{b}$ = $R_{v2}^b$($\phi$)$p^{v2}$


기체 좌표계 동체 좌표계로 변환은 다음과 같이 정리할 수 있다.
$R_v^b$($\phi , \theta , \psi$) = $R_{v2}^b$($\phi$) $R_{v1}^{v2}$ ($\theta$) $R_{v}^{v1}$( $\psi$ ) (2.4)

* $c_\phi $ = cos $\phi$, $s_\phi$=sin$\phi$
오일러 각은 물리적으로 이해하기 쉽고 많이 사용되고 있지만, 짐벌락 현상처럼 불안정하게 만드는 수학적 특이성 mathematical singularity을 가지고 있습니다. 그래서 쿼터니언은 오일러 각의 문제를 개선한 방법으로 계산도 훨씬 간단합니다.
안정성 좌표계 $F^s$
항공역학적 힘은 기체가 주위의 대기를 지나가면서 일어납니다. 이때 주변 대기에 대한 기체의 상대적인 속도를 대기 속도 벡터라 하며 $ V_a $로 표기합니다. 대기 속도 백터의 크기를 대기 속도 $ V_a $ 라 하고, 양력을 만들기 위해 기체의 날개는 대기 속도 벡터에 대해 양의 각도로 날아야만 합니다. 이때 각을 받음각 angle of attack이라 하며 $\alpha$로 표기합니다. 그림 2.8처럼 받음각은 $j^b$축에 대해 왼손 회전으로 구합니다. 왼손 회전으로 양의 받음각을 구하고, 안정성 좌표계 $i^s$ 축에서 동체 좌표계 $i^b$축으로 오른손 회전시 양의 값을 가지게 됩니다.
$\alpha$는 $F^b$에서 $F^s$로 왼손 회전으로 구하며 아래와 같이 정리할 수 있습니다.
$p^s$ = $R_b^s$ ($\alpha$) $p^b$


'로봇 > 제어' 카테고리의 다른 글
| 소형 무인 비행체 4 - 힘과 모멘트 (0) | 2020.05.30 |
|---|---|
| 소형 무인 비행체 3 - 기구학과 동역학 (0) | 2020.05.30 |
| 소형 무인 비행체 - 1 소개 (0) | 2020.05.28 |
| 제어공학 2 -25 자동차 서스펜션 제어 설계 (0) | 2020.05.11 |
| 제어공학 2 - 24 자동차 크루즈 컨트롤 설계 (0) | 2020.05.11 |