MAV의 비행, 가이드, 제어기 개발을 위해 가장 먼저 해야할 일은 동역학적 모델을 구하여야 합니다. 비행체의 비선형 운동방정식을 정리하여야 하는데 이 내용을 3장과 4장에서 다룰 것이고, 5장에서는 운동방정식을 선형화하여 제어기 설계에 알맞게 전달함수와 상태 공간 모델을 만들 것입니다.
이번 장에서는 뉴턴의 법칙($f$=$m \dot{v}$)을 이용해서 강체의 기구학과 동역학적 표현들을 정리해봅시다. 여기서는 위치와 속도 사이의 관계(기구학)과 힘과 모멘트(동역학)을 정리할 것인데 힘과 모멘트 정리때는 항공역학적인 힘과 모멘트를 주로 다룰것입니다.
상태 변수
MAV의 운동 방정식을 구하는데는 12개의 상태변수를 이용하게 됩니다. 여기서 평행 이동과 관련된 변수로 위치에 관한 변수 3개, 속도 변수 3개, 회전 운동에 대한 각자세와 각속도 상태 각각 3개가되어 총 12개의 상태변수가 존재하게 됩니다. 이 상태 변수의 목록은 아래의 테이블 1과 같습니다.
표 3.1 MAV 상태 변수들
| 이름 | 설명 |
| $p_n$ | 관성 좌표계 $F^I$ 상 축 $i^i$에 대한 북쪽 위치 |
| $p_e$ | 관성 좌표계 $F^I$ 상 축 $j^i$에 대한 동쪽 위치 |
| $p_d$ | 관성 좌표계 $F^I$ 상 축 $k^i$에 대한 아래 방향위치(고도의 음수) |
| $u$ | 동체 좌표계 $F^b$ 상 축 $i^b$ 방향에 대한 속도 |
| $v$ | 동체 좌표계 $F^b$ 상 축 $j^b$ 방향에 대한 속도 |
| $w$ | 동체 좌표계 $F^b$ 상 축 $k^b$ 방향에 대한 속도 |
| $\phi$ | 기체 2 좌표계 $F^{v2}$에 대한 롤 각도 |
| $\theta$ | 기체 1 좌표계 $F^{v1}$에 대한 피치 각도 |
| $\psi$ | 기체 좌표계 $F^{v}$에 대한 해딩(요) 각도 |
| $p$ | 동체 좌표계 $F^b$ 상 축 $i^b$에 대한 롤 각도 |
| $q$ | 동체 좌표계 $F^b$ 상 축 $j^b$에 대한 롤 각도 |
| $r$ | 동체 좌표계 $F^b$ 상 축 $k^b$에 대한 롤 각도 |

오일러각 롤 $\phi$, 피치 $\theta$, 요 $\psi$는 기체 2, 기체 1, 기체 좌표계 상에서 정의되며, 오일러 각은 기준 좌표계와 비교한 상대적인 크기일 뿐이므로, 각 속도 (p, q, r)을 각 크기($\phi$, $\theta$, $\psi$)인 의 시간에 대한 미분으로 구할수 없습니다. 하지만 아래의 내용에서는 시간에 대한 미분으로 가정해서 다뤄봅시다.
기구학
비행체의 평행이동 속도는 일반적으로 동체 좌표계 상에서 각 축에 대한 속도 요소들로 나타냅니다. 즉, 속도 변수들인 u, v, w는 관성 좌표계상 속도이지만 동체 좌표계 $i^b$, $j^b$, $k^b$ 으로사영을 해서 표현하고, 반대로 평행이동 위치는 관성 기준 좌표계 상에서 나타나게 됩니다. 평행 이동 속도와 위치 사이 관계를 정리하기 위해선 다음과 같이 미분과 회전 행렬을 이용해서 정리할 수 있게 됩니다.


위 식이 힘과 가속도를 고려하지 않은 기구학적 관계를 의미합니다.
각 위치 $\phi$, $\theta$, $\psi$와 각 속도 p, q, r 사이의 관계를 살펴보면 서로 다른 좌표계 상에 정의됩니다. 각 속도는 동체 좌표계 $F^b$ 그리고, 각 위치(오일러 각)은 세 다른 좌표계 상에서 정의 되므로 동체 좌표계 상에서 속도 변수는 오일러각의 미분과 회전 행렬로 다음과 같이 정리하여 구할 수 있습니다.

이를 역으로 정리하면 p,q,r로 다음 처럼 각속도를 구할 수 있게 됩니다.

강체의 동역학
비행체의 동역학 운동 방정식을 구하려면 뉴턴의 제 2법칙을 이용하여야 합니다. 우선은 평행 이동에 대한 3자유도를 보고나서 이후 회전 운동에 대한 자유도를 봅시다. 뉴턴의 법칙은 관성 기준 좌표계에에서 표현되는데, 즉 동체의 움직임은 고정된 좌표계 위에서 구하게 됩니다. 운동이 고정된 좌표계를 기준으로 하더라도 벡터를 다른 좌표계 상에서 나타낼 수도 있습니다. 대지 속도 벡터 $V_g$는 동체 좌표계에서 $V_g^b$ = $(u, v, w)^T$ 와 같이 일반적으로 나타 낼수 있으며 이는 동체 좌표계 상에서 땅에 대한 기체의 속도를 의미 합니다.
평행이동 운동
뉴턴의 제2 법칙을 동체의 평행이동에 적용하면 다음과 같습니다.

여기서 m은 비행체의 질량이며, $\frac{V_g}{d t_i}$는 관성 좌표계에서 시간에 대한 미분, f는 비행체에 작용하는 모든 외력의 합을 의미합니다. 이때 외력은 중력, 항공역학적인 힘, 추진력 들이 있습니다.
관성계에 대한 시간의 미분을 동체 좌표계 상에서 시간에 대한 미분과 식 2.17을 이용해서 각 속도로 다음과 같이 다시 정리할 수 있습니다.

이 때 $\omega_{b/i}$는 관성 좌표계 상에서 비행체의 각속도로 식 (3.4), (3.5)를 합쳐 관성 좌표계 상에서 시간 미분으로 힘에 대한 식을 정리 할 수 있습니다.

비행체 제어의 경우에 대해서 뉴턴의 제 2법칙으로 동체 좌표계 상에 힘과 속도를 다음과 같이 표현할 수 있습니다.
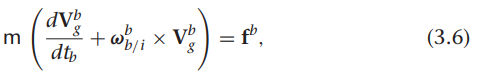
여기서, $V_g^b$ = $(u, v, w)^T$, $w_{b/i}^{b}$ = $(p, q, r)^T$ 이며, 벡터 $f^b$는 동체 좌표계 상에서 정의되는 외력들의 합으로 $f^b$ = ($f_x$, $f_y$, $f_z$)$)^T$
$\frac{\omega_{g}^{b}}{d t_b}$란 표현은 사람이 동체를 볼때 동체 좌표계 상에서 속도의 변화율로. u, v, w는 벡터 $를 $i^b$ $, $k^b$축으로사영한것이므로 아래와 같이 정리 할수 있게 됩니다.

식 (3.6)을 정리하면 결과적으로 다음의 식을 구할 수 있게 됩니다.

회전 운동
회전 운동에서 뉴턴의 제2법칙에 따라 다음의 식으로 나타낼수 있으며, 이때 h는 각 모멘텀, m은 작용하는 모멘트의 합이 됩니다.

관성 좌표계 상에서 작용하는 각 모멘텀의 미분은 식 (2.17)으로 다음과 같이 정리 할 수 있는데

평행 이동 운동 처럼, 동체 좌표계 상에 나타내는것이 편리 합니다.

강체의 각 모멘텀은 관성 행렬 J와 각속도 벡터의 내적으로 구할수 있는데
= J$\omega_{b/i}^b$
이 때 J는 다음과 같습니다.

J의 대각 성분은 관성 모멘트 moments of inertia라 부르며, 이 외 요소들을 관성 내적 products of inertia라 부릅니다. 관성 모멘트는 기체가 특정 축에 대해 회전 가속에 반대하는 힘을 의미합니다.
식 (3.8)의 각 모멘텀 $를 정리하면 다음의 식을 구할 수 있습니다.

위 식에서 J$\frac{\omega_{b/i}^{b}}{d t_b}$는 사람이 움직이는 동체를 볼때 동체 좌표계 상 각속도 변화율로, p, q, r 은 $\omega_{b/i}^{b}$의 축 $, $, $k_b$에 대한 사영이므로 아래 처럼 정리할수 있고,

식 (3.10)을 다시 정리하면

비행체는 $, $ 축으로 이루어진 평면으로 대칭이기도 하므로 이 경우 $ = $J_yz$ = 0이 되어 관성 행렬 J는 다음 처럼 정리할 수 있습니다.

이러한 대칭 가정을 이용해서 γ = $J_z$ - $$로 가정할때,J의역행렬은아래와같습니다.

결과적으로 식 (3.11)의 각 속도 변화율은 외력 $m^b$ = $과 관성 행렬 등을 이용해서 아래와 같이 정리할 수 있습니다.


'로봇 > 제어' 카테고리의 다른 글
| 소형 무인 비행체 4 - 힘과 모멘트 2 (0) | 2020.05.30 |
|---|---|
| 소형 무인 비행체 4 - 힘과 모멘트 (0) | 2020.05.30 |
| 소형 무인 비행체 2 - 좌표계 (0) | 2020.05.29 |
| 소형 무인 비행체 - 1 소개 (0) | 2020.05.28 |
| 제어공학 2 -25 자동차 서스펜션 제어 설계 (0) | 2020.05.11 |