728x90
미분방정식 이용
- 현실 -> 수학적 모델 -> 해를 구함 -> 해석
ex) 비행 시뮬레이션, 일기예보 등
비행기 위치 예측
1. 비행기 운동 미방으로 수학적 모델링
2. 시간에 대한 위치 함수
3. 비행기의 이후 위치 추정
뉴턴의 운동 방정식
- m : 질량 kg, a : 가속도 m/s, F : 힘 kg m/s

가속도를 위치에 대한 미분으로 바꿔 미방 표현
- x : 변위

y=f(x)
- f : 함수
- x : 독립 병수
- y : 종속 변수
e
- 네이피어의수
- e = 2.71828 ....
자연로그
- 밑이 e인 로그
- ln x
오일러 공식

오일러 식을 이용한 cos과 sin
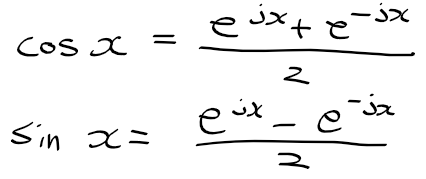
미분 방정식 분류
- 선형 : 동차, 비동차
- 비선형 : 동차, 비동차
- 미방 계수 : 가장 큰 도함수의 계수
- 미방 차수 : 가장 큰 도함수의 차수
1계 1차 미분 방정식
- 차수가 1인 변수 x에 대한 1차 미분

2계 1차 미분 방정식
- 차수가 1인 종속 변수 x에 대한 2차 미분

선형 미분 방정식
- 종속변수의 차수가 1인 미분 방정식

동차 방정식
- 미분방정식의 우항이 0

비동차 방정식
- 미분장정식의 우항이 0이 아닌 미방

진동 운동
- F(t) : 외력
- f_e : 탄성력
- f_r : 저항력
- v : 속도
- x : 변위

저항력과 탄성력
- 저항 계수가 c, 탄성 계수가 k 일때

진동 운동의 운동 방정식
- 운동 방정식 = 외력 + 저항력 + 탄성력

저항이 없는 경우 운동방정식
- 저항 계수 c = 0 대입

300x250
'수학 > 수학, 수치해석' 카테고리의 다른 글
| 수치해석 및 실습 - 3 매트랩과 2차원 그래프 (0) | 2020.06.06 |
|---|---|
| 수치해석 및 실습 - 2 매트랩과 배열 (0) | 2020.06.06 |
| 수치해석 및 실습 - 1 수치 해석과 MATLAB (0) | 2020.06.06 |
| 블로그 글에 수식 넣기 (0) | 2020.06.04 |
| 회귀 분석 기초 (0) | 2020.05.06 |