지수 함수
- e: 자연로그의 밑. 2.7182.무리수
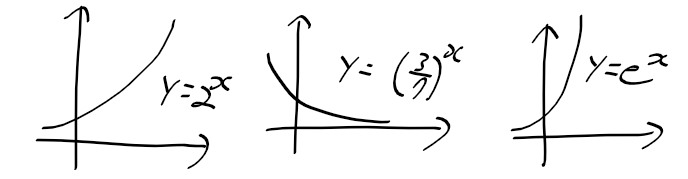
로그함수
- 지수함수의 역함수
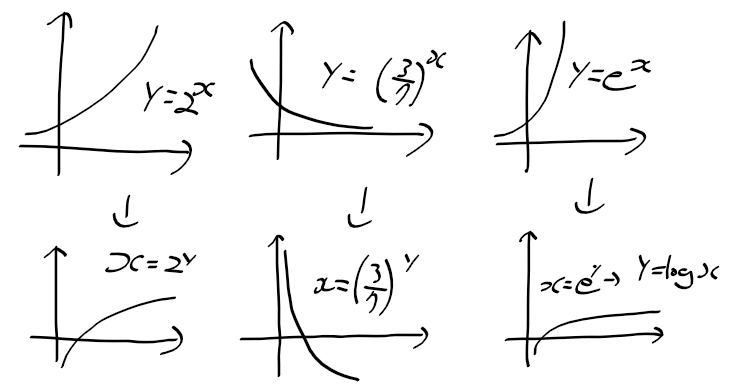
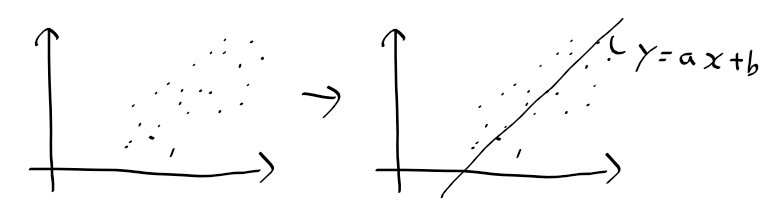
회귀식
- 회귀 분석 -> 회귀식 y=ax+b를 구함
- y : 종속변수
- x: 독리변수
- a: 회귀계수
- b: 기여율 (바이어스)
회귀 분석의 예
1. 독립 변수와 종속변수의 점 그래프 그림
2. 회귀식 구함
3. 회귀식 정도 확인
3. 회귀 계수 검정
4. 모 회귀 Ax + B 추정
5. 예측
최소 제곱법 least square method
- 모델 파라미터를 구하는 대표적인 방법
- 잔차의 제곱 합이 최소가 되도록 하는 a, b를 구해야함

최소 제곱법 계산
1. S_xx (x 편차 제곱합), S_yy (y 편차 제곱합), S_xy(xy 편자 곱합) 구함
2. S_e (잔차 제곱합) 계산
3. S_e를 a와 b에 대해 편미분 후 0으로 놓음
4. 회귀식을 구함

최소 제곱법을 이용한 회귀식

중상관계수 multiple correlation coefficeint
- 점과 회귀식이 어느정도 가까이 있는지 나타냄
- 결정계수 = R^2 (범위는 0~1)
- 회귀식에 가까울수록 결정계수가 1에 가까워짐

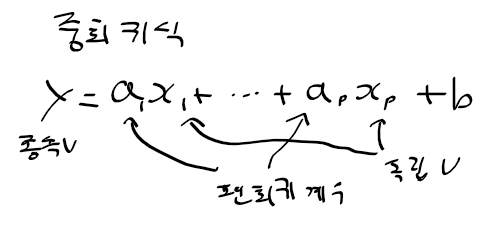
중회귀분석 multiple regression analysis
- 독립변수가 2개 이상인 회귀분석
- 중회귀식 사용
로지스틱 회귀분석 logistic regression
- 회귀분석과 달리 확률을 예측하기 위한 모델
로지스틱 회귀식
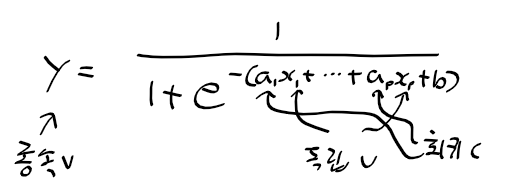
로지스틱 회귀식의 그래프 표현

최대우도법
- maximum likelihood method
- 우도 함수나 로그 우도 함수가 최대가 되는 확률 p(최우 추정값) 계산
- 확률 p가 10번 중 7번 발생하는 경우 예시
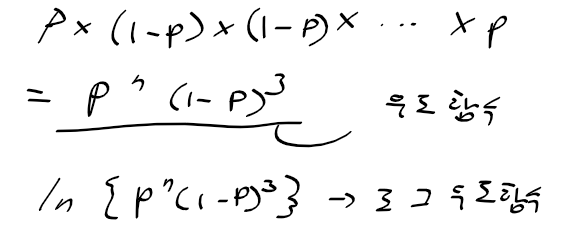

최우 추정값 계산
1. 로그 우도 계산
2. 로그우도 함수를 구하고 정리
3. 로그 우도 함수 L을 p에 대해 미분하고, 0과 대응
4. 위 식을 정리하여 최대 우도 p를 계산 가능

로지스틱 회귀식 계산
1. 추정 값 계산
2. 우도 함수 계산
3. 로그 우도 함수 계산
4. 최우 추정값 계산 -> 회귀 계수 a와 편향 b 구함
5. 회귀 식 정리

오즈 odds
- 사건 A가 (발생확률)/(발생하지 않을 확률) 비
- P(A)가 1에 가까울수록 오즈는 커짐

로짓 logit
- 오즈에 자연로그를 취한것

'수학 > 수학, 수치해석' 카테고리의 다른 글
| 수치해석 및 실습 - 3 매트랩과 2차원 그래프 (0) | 2020.06.06 |
|---|---|
| 수치해석 및 실습 - 2 매트랩과 배열 (0) | 2020.06.06 |
| 수치해석 및 실습 - 1 수치 해석과 MATLAB (0) | 2020.06.06 |
| 블로그 글에 수식 넣기 (0) | 2020.06.04 |
| 미분 방정식 기초 (0) | 2020.05.15 |