이번 장에서는 비행체에 작용하는 힘과 모멘트를 다루려고 합니다. 이 힘과 모멘트는 주로 중력, 항공역학적힘, 추진력에 의해 작용하게 돕니다. $F_g$는 중력에 의한 힘, ($f_a, m_a$)는 항공역학적 힘과 모멘트, ($f_p, m_p$)는 추진력에 의한 힘과 모멘트가 됩니다. f를 비행체에 작용하는 힘의 총합, m은 모멘트 총 합이라면 다음과 같이 정리 할수 있습니다.
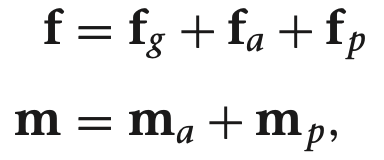
이 장에서 힘과 모멘트 각각에 대해 설명할 것이며 4.1장에선 중력, 4.2장에서는 항공역학적 힘과 토르크, 4.3은 추진에 의한 힘과 모멘트, 4.4장에서는 대기 요란 atmospheric disturbance을 다루겠습니다.
4.1 중력
기체에 작용하는 중력은 질량의 크기에 비례하도록 설계할 수 있습니다. 이 힘은 $k^i$ 방향으로 작용하며 중력 상수 g와 기체의 질량에 비례하게 됩니다. 기체 좌표계 $F^v$ 상에서 중력은 질량의 중심에 작용하며, 다음 처럼 나타 낼 수 있습니다.
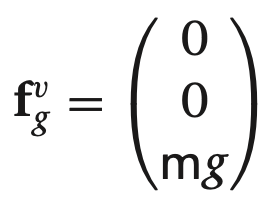
이 식은 3장에서 본 뉴턴의 제 2법칙에 따라 동체 좌표계 상으로 정리해야 하며, 중력을 동체 좌표계의 요소로 정리하면 다음과 같습니다.
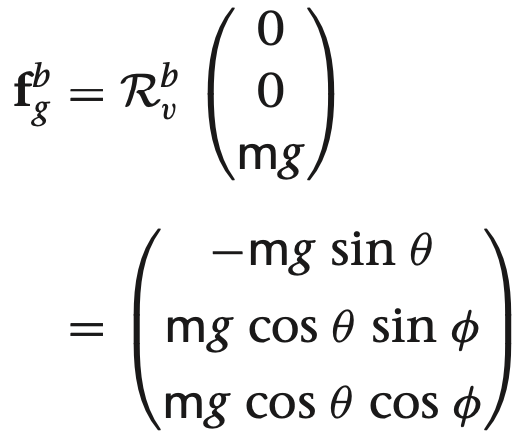
4.2 항공역학적 힘과 모멘트
비행체가 대기를 지나가면서, 그림 4.1처럼 몸체 주위로 압력 분포가 나타나게 됩니다. 비행체에 작용하는 압력의 크기와 분포가 대기 속도와 대기 밀도, 고도로 이루어진 함수가 됩니다. 이 때 작용하는 압력은 $\frac{\rho }{V_a^2}$가 되며, $\rho$는 대기 밀도, $V_a$는 대기상 비행체의 속도 입니다.
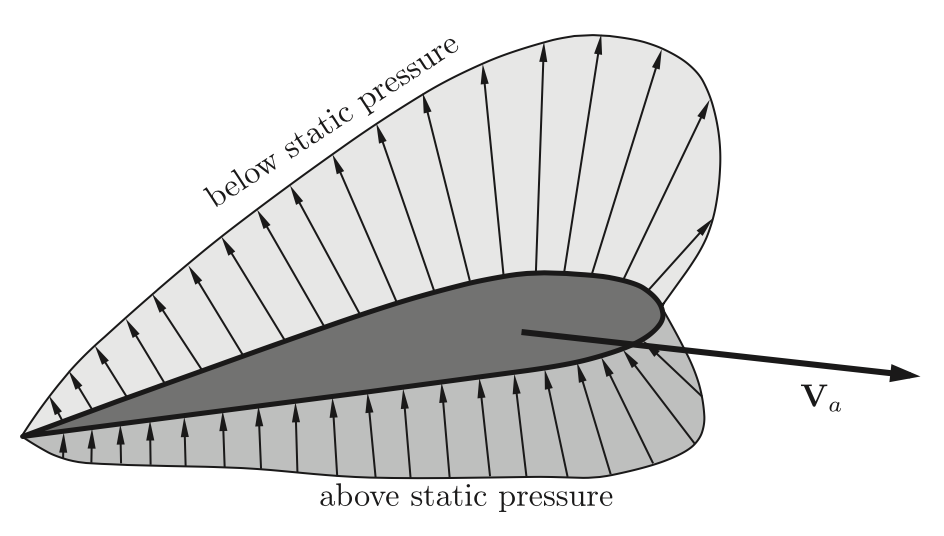
이 처럼 날개 주위의 압력 분포 특성을 정리하는것 보다 일반적인 접근 방법은 이 압력에 의한 힘과 모멘트의 영향을 정리하면 됩니다. 예를 들어 $i^b$-$k^b$으로 이루어진 종방향에서는 동체에 작용하는 압력들로 양력 lift force, 항력 drag force, 모멘트가 있습니다. 그림 4.2처럼 양력과 항력은 항공역학적 중심이라 할수 있는 날개 현의 1/4 지점 quater-chord point에서 작용하게 됩니다.
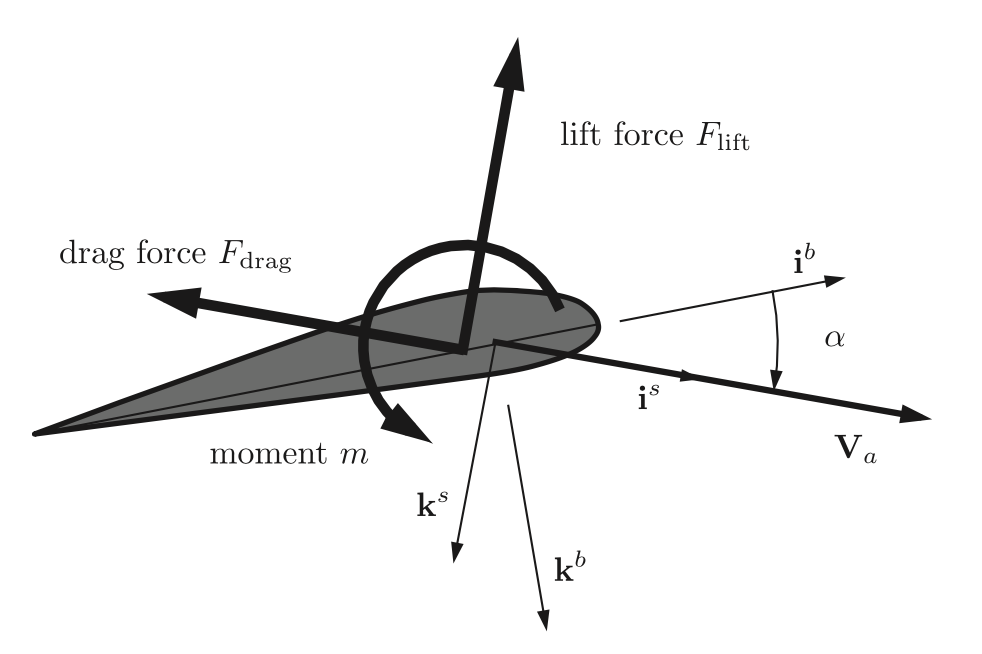
이 때, 양력과 항력, 모멘트는 다음과 같이 정리 할 수 있는데
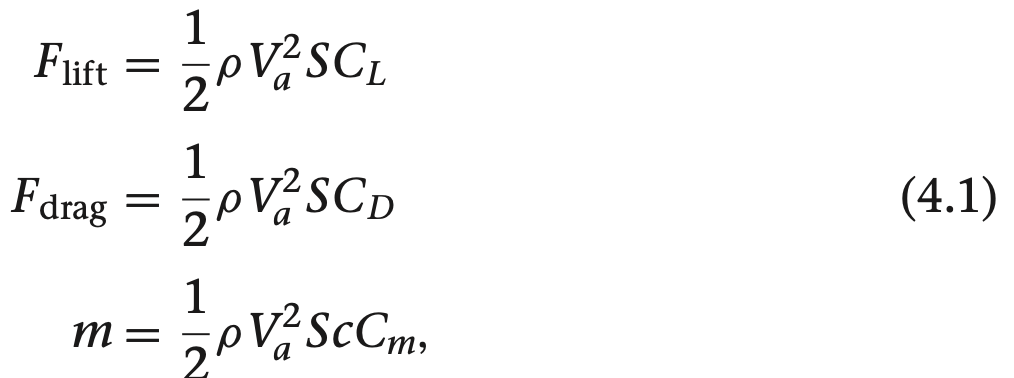
여기서 $C_L, C_D, C_m$은 무차원 항력계수 nondimensional aerodynamic coefficients, S는 비행체 날개 면적, c는 날개 현 길이의 평균이 됩니다. 양력, 항력, 피칭 모멘트는 날게의 형태와 레이놀드 수, 마하 수, 받음각에 크게 영향을 받게 됩니다. 소형 비행체 주위에 일정한 대기 속도가 작용하면 레이놀드 수와 마하 수의 영향은 상수가 됩니다. 이후에는 받음 각 $\alpha$와 sideslip $\beta$, 각 속도 p, q, r, 제어면 control surface 접힘정도에 의한 영향을 살펴보겠습니다.
이렇게 항공역학적인 힘과 모멘트를 다룰때 종방향과 횡방향으로 분해해서 다루는게 일반적이고, 종방향의 힘과 모멘트는 피치 평면이라 부르는 $i^b$-$k^b$ 평면에서 작용하며, $i^b$, $k^b$ 방향으로 작용하는 양력과 항력같은 힘과 $j^b$축 방향으로 작용하는 모멘트로 이루어 집니다. 측면에 대한 힘과 모멘트는 $j^b$ 방향으로 작용하는 힘과 $i^b$, $k^b$ 축에 대한 모멘트로 이루어 집니다.
4.2.1 제어면
항공역학적 힘과 모멘트에 대한 상세한 방정식을 다루기 전에, 비행체 조종에 사용되는 제어면 control surface에 대해 알아봐야 합니다. 제어 면은 항공역학적인 힘과 모멘트를 바꾸는데 사용하며, 일반적인 비행기의 경우 제어면으로 엘리베이터 elevator, 에일러론 aileron, 러더 rudder가 있으며 다른 비행체의 경우 스포일러와 플랩, 카나드 등이 있지만 이 책에서 다루지는 않지만 비슷하게 설계할 수 있습니다.
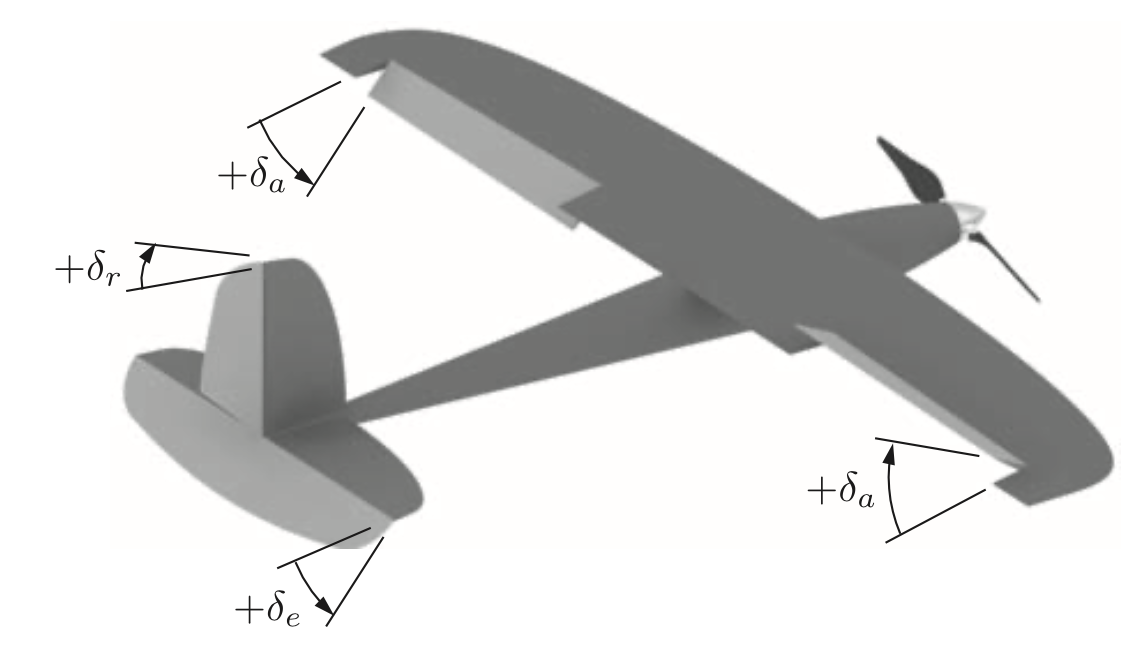
그림 4.2은 일반적인 비행기의 경우를 보여주며, 에일러론 접힘 aileron deflection은 $\delta_a$, 엘리베이터 접힙 elevator deflection은 $\delta_e$, 러더 접힘 rudder deflection은 $\delta_r$로 표기합니다. 제어면의 양방향 접힘은 제어면의 힌지 축에서 오른손 규칙을 따르며, 엘리베이터의 힌지 축은 동체 $j^b$축과 나란하므로 오른손 법칙에 따라 엘리베이터가 아래로 내려갈때 양의 접힘값을 가지게 됩니다. 비슷하게 러더가 왼쪽으로 향할때 양의 접힘이 됩니다. 마지막으로 에일러론 접힙 $\delta_a$는 접힘값을 정리하여 다음과 같이 구할 수 있습니다.
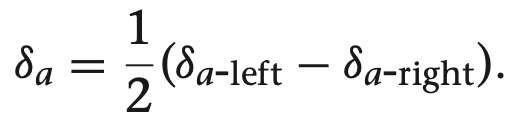
그러므로 양의 $\delta_a$는 왼쪽 에일러론이 내려가고 오른쪽 에일러론이 올라갈때 생기게 됩니다.
4.2.2 종방향 항공역학
종방향 항공역학적 힘과 모멘트는 피치 평면인 $i^b$-$k^b$에서 작용하며, 양력과 항력, 피치 모멘트 처럼 친숙한 요소들입니다. 양력과 항력을 정의하면 그림 4.2에서 안정성 좌표계의 축과 나란하게 작용하며, 벡터에서 볼때 피치 모멘트는 안정성 좌표계의 $j^s$축과 나란하게 됩니다.
양력과 항력, 피치 모멘트는 받음각에 크게 영향을 받는데, 피치 속도 q와 엘리베이터 접힘 $\delta_e$ 역시 종방향 힘과 모멘트에 영향을 줍니다. 이 개념들을 정리해서 양력과 항력, 피치 모멘트에 대한 $\alpha$, q, $\delta_e$의 함수로 아래와 같이 정리 할 수 있습니다.

보통 이러한 힘과 모멘트 방정식은 비선형이며, 받음각이 작은 경우, 날개 주위의 대기 히름이 평평하게 됩니다. 이런 상태에서 양력과 항력, 피치 모멘트는 선형 추정으로 적당히 정확하게 모델을 만들수 있게 됩니다. 양력에 대한 방정식의 경우 1차 태일러 급수 추정 first order taylor series approximation으로 다음과 같이 정리 할 수 있습니다.
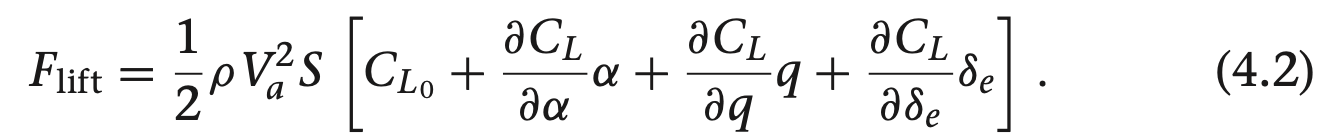
여기서 $C_{L0}$는 $\alpha$ = q = $\delta_e$ = 0 일 때 $C_L$ 값으로, 선형 추정의 편미분을 무차원화할때 사용됩니다. $C_L$과 $\alpha$, $\delta_e$는 차원이 없으므로, $\frac{C_L}{\delta q}$만 무차원화가 필요합니다. q의 단위는rad/s 이므로, 정규화 시키기 위해 $\frac{c}{2 V_a}$를 사용하여 식 4.2를 다음과 같이 다시 정리할 수 있습니다.
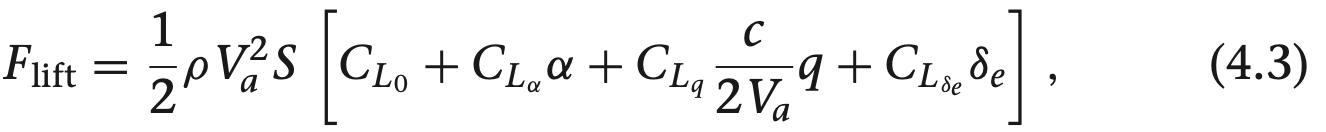
위 식의 계수들은 아래와 같으며 무차원의 크기를 나타냅니다.
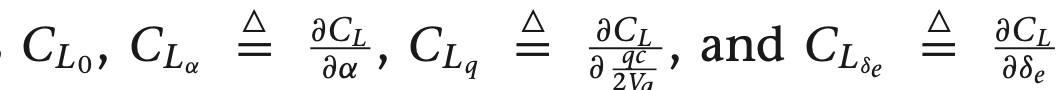
$C_{L_{\alpha}}$, $C_{L_{q}}$는 안정성 미분 계수이며, $C_{L_{\delta_{e}}}$여기서 미분 계수는 테일러 급수 추정에서 편미분 요소로 구하며, 이와 같은 방식으로 항력과 피치 모맨트 선형 추정을 구할 수 있습니다.
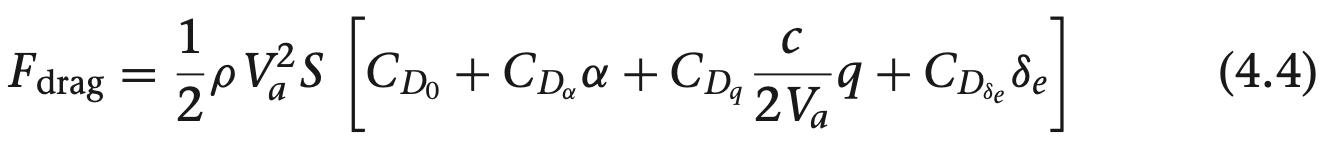
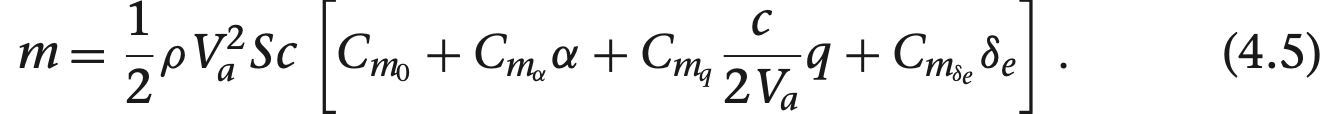
식 (4.3), (4.4), (4.5)는 종방향 항공역학적 모델의 기반이 되며, 받음각이 작은 상태일 때는 힘과 모멘트를 정밀하게 구할 수 있습니다. 이 때 기체 주위로 층류가 흘러 주위 대기 흐름이 안정적으로 흐르게 되어 받음각이나 피치 속도 엘리베이터 접힘 크기가 변하더라도 대기 흐름을 예측 할 수 있고, 신뢰할수 있게 됩니다. 불안정 상태의 특징으로 비선형이고, 3차원, 시변, 큰 흐름의 변화가 있습니다.
기체 제어시 MAV 개발자는 받음 각이 높은 겨우와 각속도가 큰 경우와 같은 두 불안정 한 경우를 고려해야 하여야 합니다. 가장 중요하게 고려야해하는 불안정 현상으로 스톨이 있으며, 스톨은 받음 각이 증가하여 대기의 흐름이 나눠질 때 발생하여 양력을 급격히 떨어트립니다.
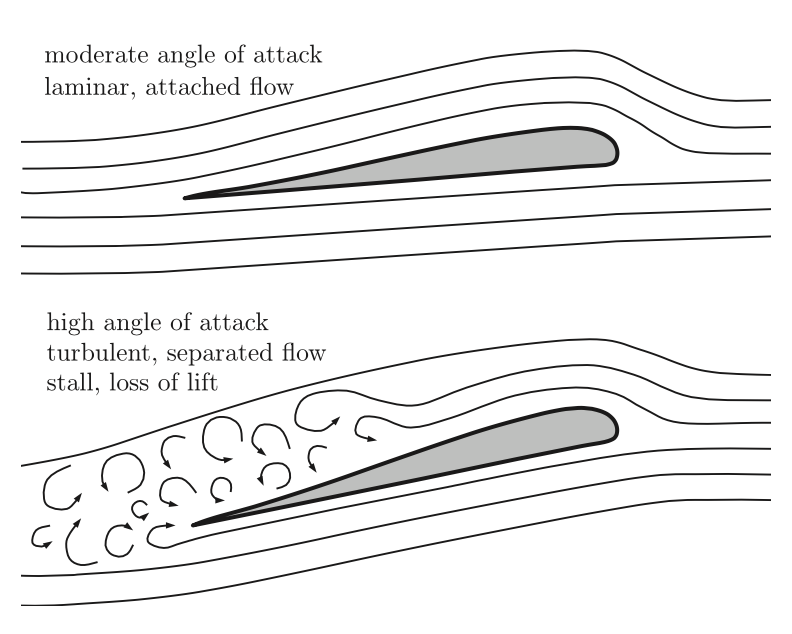
스톨 상태에서 식 (4.3), (4.4), (4.5)로 구한 추정 값은 매우 위험할 수 있는데, 날개 주위에서의 스톨 현상은 그림 4.6와 같습니다. 받음각이 작으면 날계 주위의 대기가 안정적이지만, 받음각이 스톨 한계 각 critical stall angle을 넘기면 대기의 흐름나 분산되면서 동요를 일으키며 양력이 급격히 떨어지게 됩니다.
받음각이 계속 증가할 때 양력이 증가하는걸로 예측하는것은 물리적으로 비현실입니다. 여거 설명하는 동역학 모델은 스톨의 영향 또한 종방향 역학 모델에 포함시키는 것이 중요합니다.
날개 스톨을 추가 하기 위해선 받음각에 대해 양력과 항력이 비선형이 되도록 식 (4.3), (4.4)를 바꾸어야 합니다. 이러면 더 넓은 범위의 $\alpha$에서 양력과 항력을 구하는 모델이 되며 아래와 같습니다.
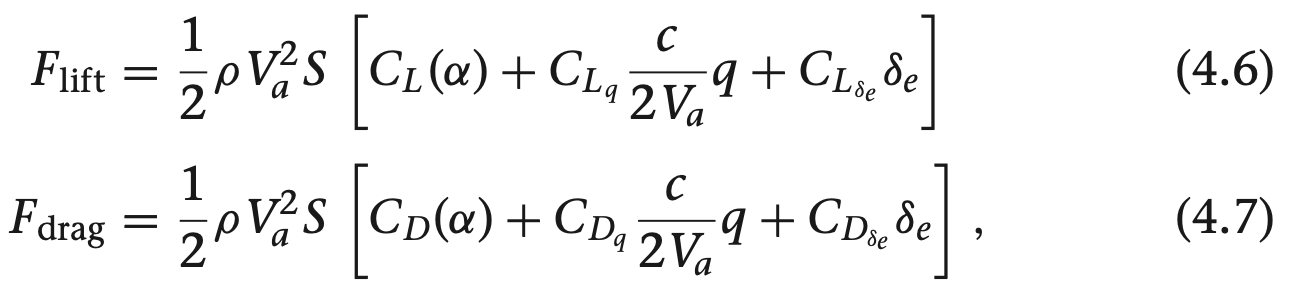
이 때, $C_L$, $C_D$는 받음각 $\alpha$에 대한 비선형 함수가 되어, 받음 각이 스톨 상태를 넘어갈때 날개는 거칠게 동작하지만 양력 계수는 아래의 식으로 모델링 할수 있습니다.
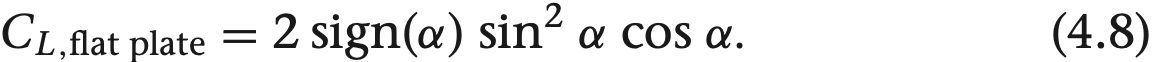
대부분의 시뮬레이션에서는 특정 상황에 대해 높은 정확성을 요구하지 않기 때문에 이정도의 스톨 영향을 반영하는게 적당합니다. 선형 양력과 스톨의 영향을 합친 양력 모델은 다음 처럼 정리할 수 있습니다.
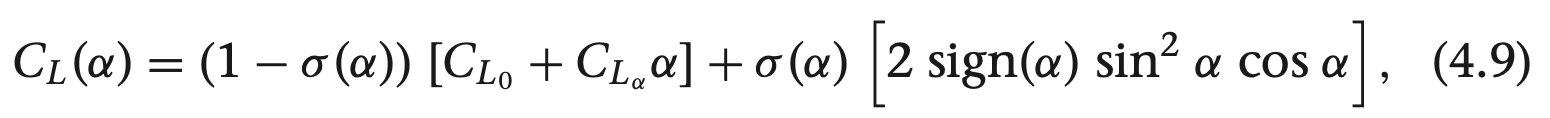
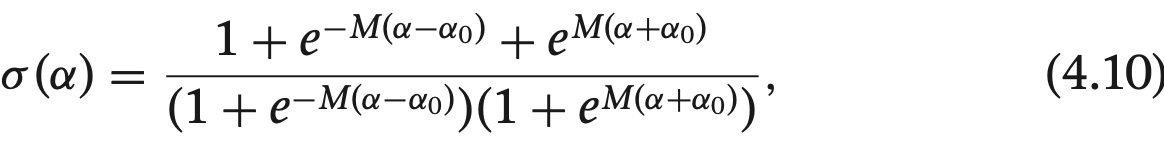
위 식에서 M과 $\alpha_{0}$은 양의 상수이고, 식 (4.10)에서 시그모이드 함수는 $\alpha_{0}$에서 컷오프하고 이동 비율 M으로 만들어 집니다.
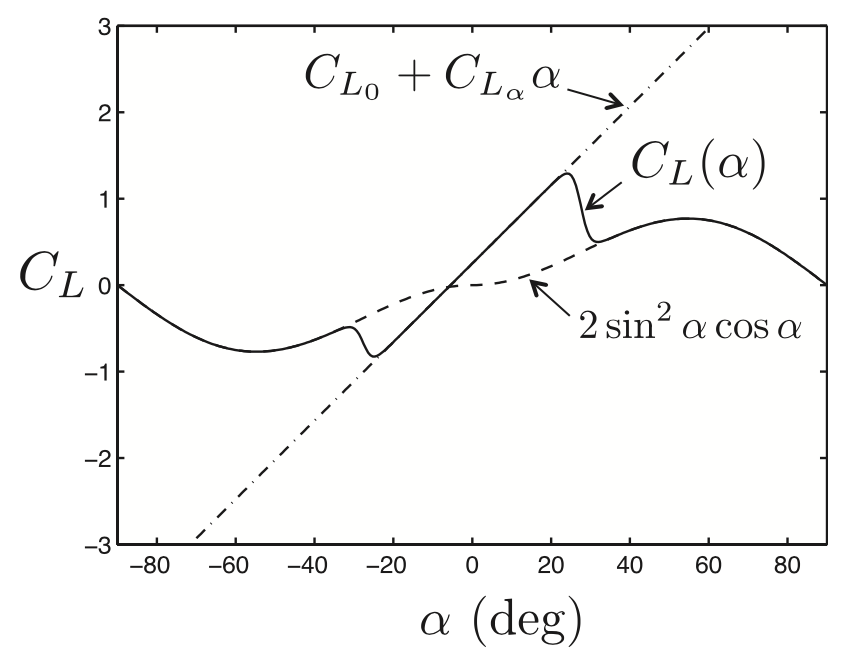
그림 4.7은 식 (4.9)에서 $C_{L0}$ + $C_{L_{\alpha}}$ $\alpha$를 이용하여 구한 양력 계수와 식 (4.8)에서 구한 평판에서의 양력 계수가 됩니다. 소형 비행체에서 선형 양력 계수는 아래와 같이 정리 할수 있는데, 이 때 AR = $b^2$/S는 날개의 종횡 비, b는 날개 길이, S는 날개 면적이 됩니다.
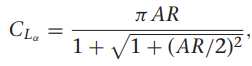
항력 계수 $C_D$도 받음각에 대한 비선형 함수로 항력과 기생 항력 parastic drag를 발생시킵니다. 기생 항력이란 날개와 다른 요소로 발생하는 항력으로 대략적인 상수 값이 되며 $C_{D_p}$로 표기합니다. 받음 각이 작을 때 항력은 양력의 제곱에 비례하며, 항력과 기생 항력을 다음과 같이 정리할 수 있습니다.
위 식에서 e는 오즈왈드 값 oswald efficency factor로 0.8 ~ 1.0 사이 값을 가지게 됩니다.
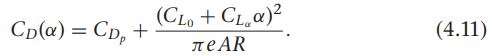
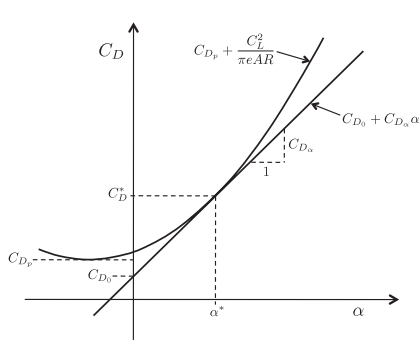
그림 4.8은 받음 각에 대한 항력 계수의 이차/선형 모델을 보여주는데, 이차 모델이 받음각에 대해 정확하게 항력을 모델링 할 수 있습니다. 선형 모델은 비행기가 아래를 향하여 받음각이 음수가 되면 항력을 음수로 잘못 예측하게 됩니다. 기생항력 $C_{D_p}$와 구분하자면, 기생 항력은 양력이 0일때의 항력 계수 $C_{D_0}$와 같습니다. 파라미터 $\alpha^*$와 $C_D^*$는 $C_D$가 선형화되어 $\alpha$=$\alpha^*$인 지점에서의 받음각과 항력 계수가 됩니다.
이차 모델은 넓은 범위의 받음각의 영향을 정밀하게 나타낼수 있으나 선형 모델이 간편하고 일반적인 비행상태의 경우 정확하므로 주로 사용되기도 합니다.
식 (4.6)과 (4.7)에서의 항력과 양력은 안정성 좌표계에서 표현하며, 동체 좌표계에서 나타내기 위해 받음각으로 회전이 필요합니다.
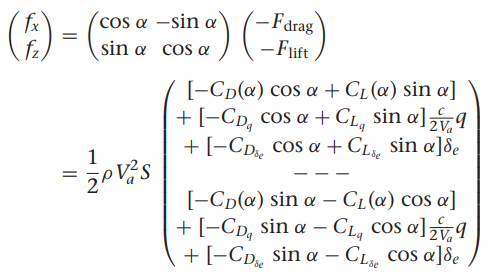
함수 $C_L$($\alpha$), $C_D$($\alpha$)는 식 (4.9), (4.11)에서 나타낸 비선형 함수로 구한 힘 모델이며, 단순한 모델이 필요하다면 아래와 같은 선형 계수 모델을 사용할수 있습니다.
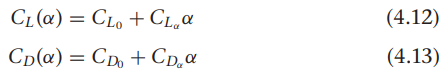
비행체의 피칭 모멘트는 받음각에 대한 비선형 함수이고, 시뮬레이션 용도로 다음의 선형 모델을 사용하겠습니다.
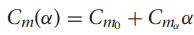
4.2.3 횡방향 항공역학
횡방향 힘과 모멘트는 측면 $j^b$ 방향에 대한 평행 이동과 롤과 요가 변하는 회전 운동을 일으킵니다. 이때 횡방향 항공역학은 사이드 슬립 각 $\beta$에 크게 영향을 받으며, 롤 변화율 p, 요 변화율 r, 에일러론 접힘 $\delta_a$와 러더 접힘 $\delta_r$ 등의 영향을 받습니다. 측면 힘을 $f_y$, 롤과 요 모멘트를 각각 l과 n이라고 한다면. 다음의 식으로 정리할 수 있습니다.
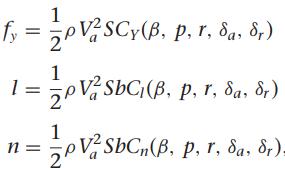
여기서 $C_Y$, $C_l$, $C_n$는무차원항공역학적계수이며,b는날개 길이가 됩니다. 종방향 항공역학적 힘과 마찬가지로 $C_Y$, $C_l$, $C_n$는 $\beta$, p, r, $\delta_a$, $\delta_r$에 대한 비선형 함수 파라미터 들이나 특성을 정리하기 어려우무로 선형 모델을 사용하게 됩니다. 4.2.2장에서와 같이 1차 태일러 급수 추정과 항공역학적 계수의 무차원화 과정으로 측면 힘과 롤/요 모멘트를 아래와 같이 정리할 수 있습니다.
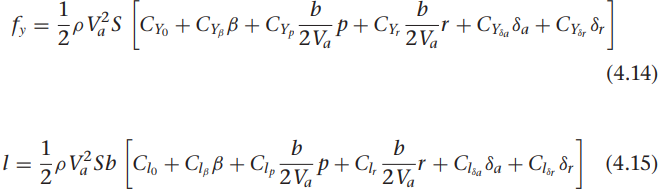
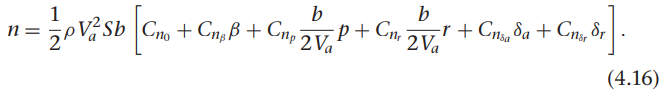
이러한 힘과 모멘트는 동체 좌표계의 축과 나란하게 작용하여 회전 변환이 필요하지는 않습니다.
'로봇 > 제어' 카테고리의 다른 글
| 소형 무인 비행체 5 - 선형 모델 설계 (0) | 2020.05.31 |
|---|---|
| 소형 무인 비행체 4 - 힘과 모멘트 2 (0) | 2020.05.30 |
| 소형 무인 비행체 3 - 기구학과 동역학 (0) | 2020.05.30 |
| 소형 무인 비행체 2 - 좌표계 (0) | 2020.05.29 |
| 소형 무인 비행체 - 1 소개 (0) | 2020.05.28 |