오토파일럿이란 비행체를 조종사 없이 안내하는 시스템을 의미합니다. 유인 비행체에서 오토파일럿은 단순한 단일 축의 윙레벨 오토파일럿에서 다양한 비행 상태(이륙, 상승, 레밸 비행, 하강, 접근, 착륙)동안 고도, 경도, 위도 같은 위치와 롤, 피치, 요와 같은 자세를 제어하는 복잡한 완전 비행 제어 시스템도 있습니다.
MAV에서는 모든 비행 단계들에서 비행체 제어를 오토파일럿이 해야합니다. 일부 제어 기능을 지상국에서 할수도 있지만 오토파일럿의 대부분 제어 시스템은 MAV 내부에 있습니다.
이번 장에서는 센서와 MAV 내부에서 계산 가능하도록 적합한 오토파일럿 설계법을 살펴보겠습니다. 여기서 횡방향과 종방향 오토파일럿을 설계하기 위해서 연속 폐루프 succesive loop closure라고 부르는 방법을 사용할건데, 이는 6.1에서 다루어 보겠습니다.
비행체의 양력 면은 점위가 제한되므로 액추에이터 포화도 actuator saturation와 거기에서의 성능 제한을 6.2에서 살펴보겠습니다. 횡방향과 종방향에 대한 오토파일럿 설계법은 6.3장과 6.4장에서 다루어 보고, 6.5에서 이산 시간에 대한 비례-적분-미분 피드벡 제어 법칙을 따르는 제어기에 대해 살펴보면서 마치겠습니다.
6.1 연속 폐루프 Successive Loop Closure
오토파일럿 설계에서 주요 목표는 관성 위치($p_n$, $p_e$, h)와 자세($\phi$, $\theta$, $\chi$)를 제어하는것입니다. 대다수의 비행 제어기에선, 동역학식을 분리하여 설계한 오토파일럿은 좋은 성능을 보입니다. 종방향 동역학(전진 속도, 피칭, 상승, 하강 운동)과 횡방향 동역학(롤링, 요잉 모션)을 나누어 다루어 보겠습니다. 이를 통하여 오토파일럿 설계를 단순화 시키며, 순차 폐루프라 부르는 오토파일럿 설계 방법을 사용할 수 있게 됩니다.
연속폐루프의 기본 개념은 하나의 복잡한 제어 시스템을 설계하기 보다는, 여러개의 단순한 피드백 폐루프를 개루픞 플랜트 주변에 연속적으로 연결한 것이 됩니다.
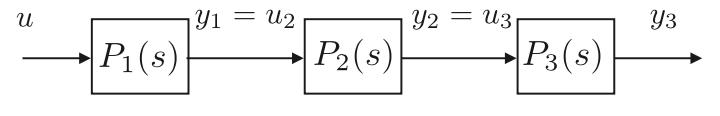
그림으로 살펴보면 그림 6.1의 개루프 시스템을 다뤄보겠습니다. 개루프 동역학식은 세개의 전달함수를 직렬로 곱하여 구하는데 P(s) = $P_1$(s) $P_2$(s) $P_3$(s)이됩니다. 각각의 전달함수는 출력으로 $y_1$, $y_2$, $y_3$이 나오며 이를 측정하여 피드벡에서 사용됩니다. 여기서 $P_1$(s), $P_2$(s), $P_3$(s) 전달함수 각각은 1, 2차로 상대적으로 저차수가 됩니다.
이 경우 우리가 제어에서 관심가져야 할 것은 출력 $y_3$이 됩니다. $y_3$ 하나만을 궤환시키는 대신 그림 6.2처럼 $y_1$, $y_2$, $y_3$을 연속적으로 피드백을 시키겠습니다. 보상기 $C_1$(s), $C_2$(s), $C_3$(s)를 설계할 건데 설계 과정의 필수 조건은 내부 루프가 가장 큰 대역폭을 가지고, 각각의 연속 루프 대역폭 요소는 주파수대가 5~10배 정도 작아야 합니다.
그림 6.2의 내부 루프를 살펴보면 폐루프 설계 목표는 $r_1$로부터 $y_1$을 출력하는 대역폭이 $\omega{BW1}$인 폐루프 시스템을 설계하고자 합니다.
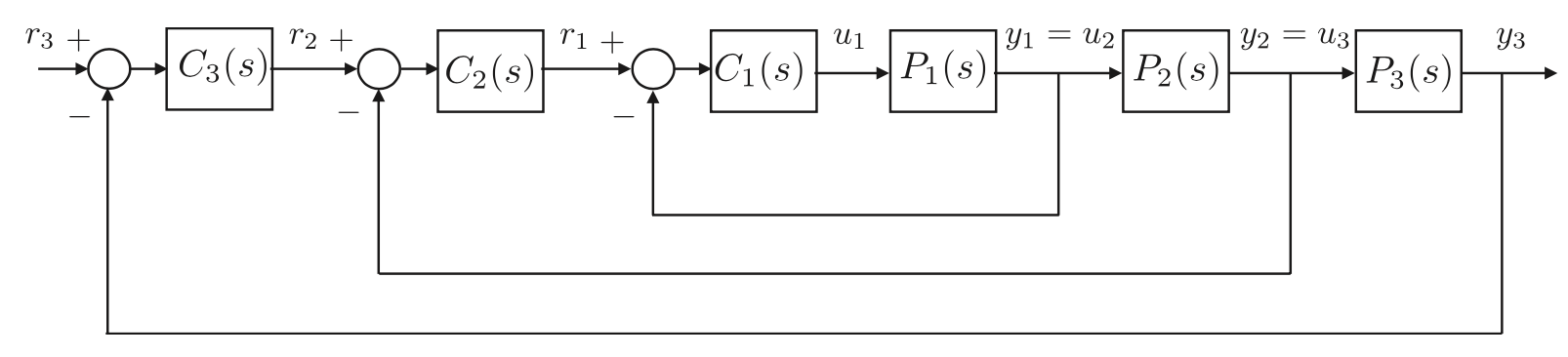
폐루프 전달함수 $y_1$(s) / $r_1$ (s)는 이득을 1로 설계할수 있는데 그림 6.3와 같습니다. 이 내부 전달함수의 이득을 1로 설계하면, 두번째 루프는 플랜트 전달함수 $P_2$(s)와 보상기 $C_2$(s)이므로 단순화 시킬수 있습니다. 연속 루프를 닫는데 있어 중요한 과정은 다음 루프의 대역폭을 이전 루프것보다 5 ~ 10배 정도 작게 설계하여야 합니다. 우리의 경우 $\omega_{BW2}$ < $\frac{1} {s}$면 됩니다.
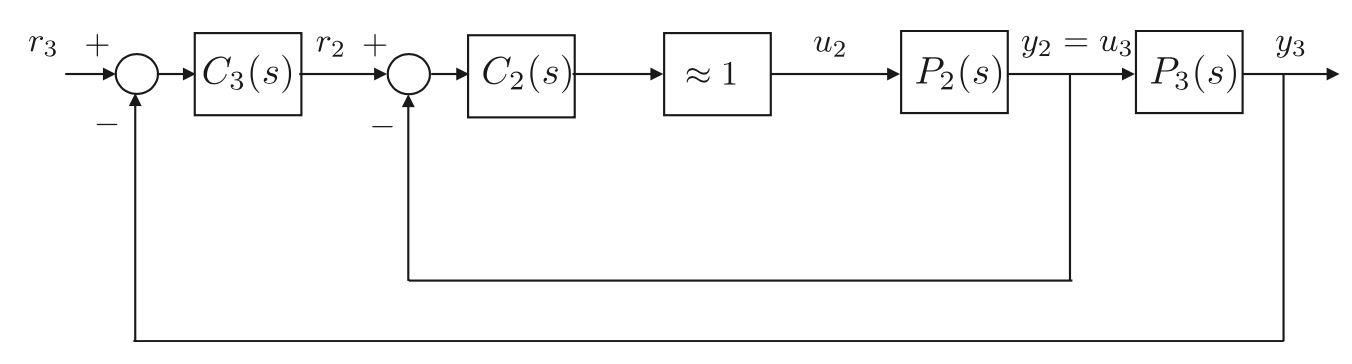
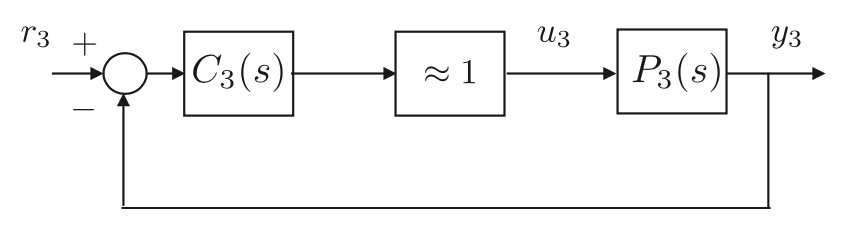
두 개의 내부 루프를 $y_2$(s) / $r_2$(s) $\approx$ 1이 되도록 설계하면, $r_2$(s)에 대한 $y_2$(s)의 전달함수는 그림 6.4처럼 가장 바깥 루프에 대한 게인 1로 바꿀수 있습니다.
외부 루프의 대역폭 제한이 있으므로 $\omega_{BW3}$ < $\frac{1} {s^2}$ $\omega_{BW2}$가 됩니다. 각각의 플렌트 모델 $P_1$(s), $P_2$(s), $P_3$(s)는 1 또는 2차이므로 기존의 PID나 뒤섬 보상기가 효율적입니다. 루트 로커스나 루프 형태 같은 전달함수 기반 방법을 주로 사용이 됩니다.
이후 장에서 횡방향과 종방향 오토파일럿 설계 방법에 다루겠습니다. 5.4장에서 횡방향/종방향 동역학 모델링하는 전달함수를 개발하고 오토파일럿 설계에 사용하겠습니다.
6.2 제한 포화도와 성능 saturation constraint and performance
연속 폐루프 디자인 과정에서 시스템의 성능은 내부 루프의 성능에 따라 제한이 됩니다. 가장 안쪽의 루프 성능은 제한 포화도로 제한이 될수 있습니다.
예를 들어 횡방향 오토파일럿 설계시 에일러론은 접을수 있는 각에 물리적으로 제한이 될수 있는데 이는 비행체의 롤 변화율이 제한됨을 의미합니다. 여기서 목표는 내부 루프 대역폭을 포화도 제한을 위반하지 않도록 가능한 크게 설계하는것이고, 바깥 루프를 연속 루프의 대역폭에 맞게 설계하는것입니다.
이번 장에서 간단하게 플랜트와 제어기 전달함수, 액추에이터 제한 포화도에 대한 지식들이 가장 안쪽 루프의 성능 스펙을 구하는대 사용하는지 알아보겠습니다. 이 과정을 2차 시스템을 사용하여 설명하겠습니다.
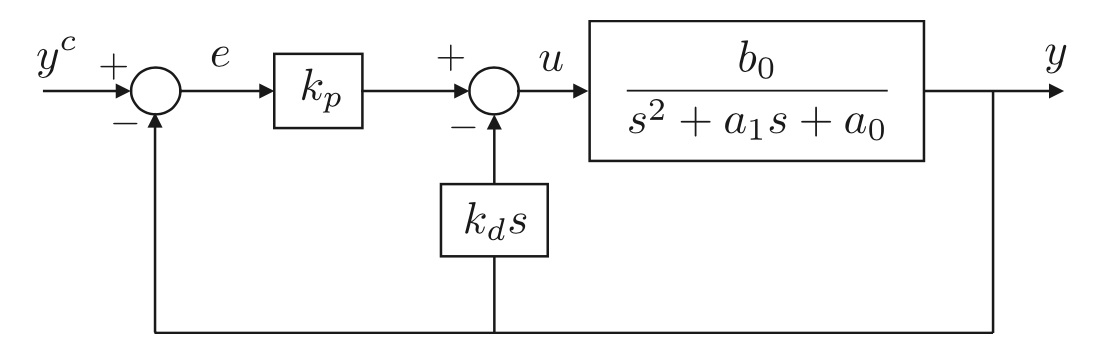
그림 6.5같은 출력 오차를 비례 피드백하고, 출력을 미분 피드백하는 2차 시스템이 주어질때, 이 폐루프 전달함수는 아래와 같고
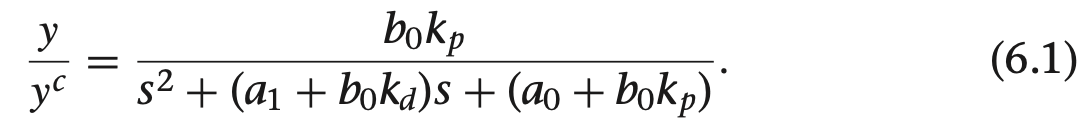
이 폐루프 시스템의 극점이 제어기 게인 $k_p$, $k_d$에 의해 정해지는것을 알수 있습니다. 액추에이터 힘 u는 u = $k_p$ e - $k_d$ $\dot{y}$로 나타낼수 있는데, $\dot{y}$는 0이거나 작을 때 엑추에이터 입력 u의 크기는 제어기 오차 e와 제어기 게인 $k_p$로 조정할 수 있습니다.
이 시스템이 안정하다면 스템 입력에 대한 가장 큰 제어기 입력 응답은 $u^{max}$ = $k_p$ $e^{max}$에서 스텝이 들어간 직후에 발생할 것입니다. 이 내용을 다시 정리하면 비례제어기 계인을 최대 기대 출력 오차와 엑추에이터의 포화도 제한으로 구할수 있는데 식은 다음과 같습니다.

여기서 $u^{max}$는 시스템이 가능한 최대 제어 입력이고 $e^{max}$는 스텝 입력에 대한 스텝 오차를 의미합니다.
영점이 없는 표준 2차 전달함수는 다음과 같은 표준 형태로 정의되는데 $y^c$는 제어 입력이고, $\zeta$는 댐핑비, $\omega_n$는 고유진동수를 의미합니다.
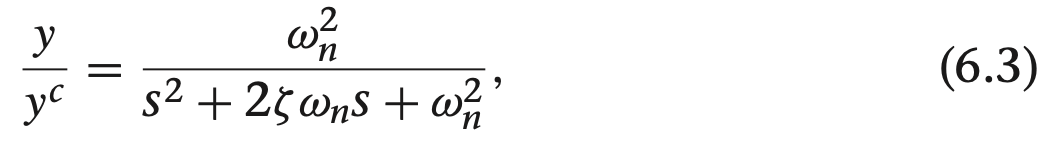
여기서 0 <= $\zeta$ <= 1 이면, 이 시스템은 과소 감쇄 under damped이며, 극점은 복소수로 다음과 같습니다.
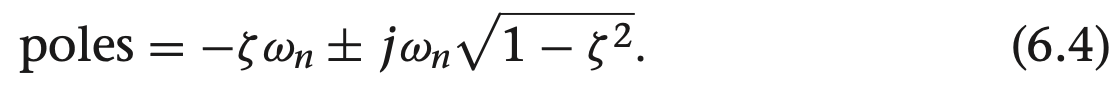
식 (6.1)에서 폐루프 시스템 전달함수의 분모 다항식 계수들을 식 (6.3)에서 표준 2차 전달함수를 엑추에이터의 포화도 제한을 고려하여 비교하면, 사용가능한 폐루프 대역폭에 대한 구할수 있습니다.
$s^0$ 항의 계수를 같다고 한다면 다음과 같이 정리할수 있는데
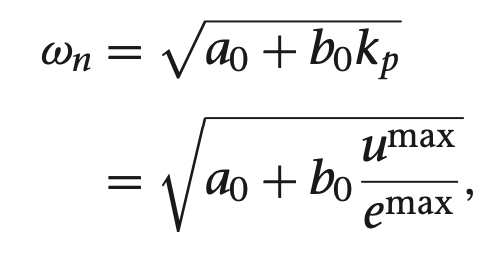
이는 폐루프 시스템 대역폭의 상한선이 되며 엑추에이터의 포화도가 이 값이 되어서는 안됩니다. 6.3.1, 6.4.1장에서 이를 이용하여 롤과 피치 루프의 대역폭을 설정하는데 사용해보겠습니다.
'로봇 > 제어' 카테고리의 다른 글
| 소형 무인 비행체 2 - 과제 (0) | 2020.06.02 |
|---|---|
| 소형 무인 비행체 6 - 연속 폐 루프로 오토파일럿 설계하기2 (0) | 2020.06.01 |
| 소형 무인 비행체 5 - 선형 모델 설계 2 (0) | 2020.06.01 |
| 소형 무인 비행체 5 - 선형 모델 설계 (0) | 2020.05.31 |
| 소형 무인 비행체 4 - 힘과 모멘트 2 (0) | 2020.05.30 |