연속 확률 변수를 따르는 확률 분포
- 연속 균등 분포
- 지수분포
- 정규분포
연속 균등 분포
- 구간에 의해 결정되며, 균등한 확률값을 가지는 확률 분포
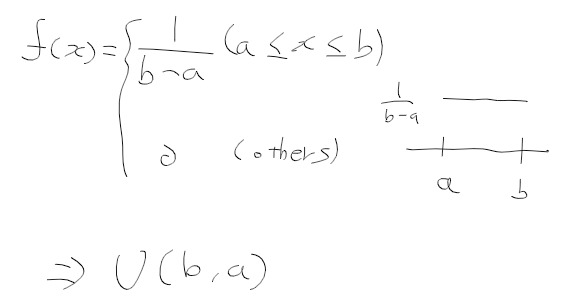
지수 분포와 포아송 분포
- 일정 기간 사건 발생 횟수에 대한 확률 분포 -> 포아송
- 사건 발생 시간 사이 시간(수명)에 대한 확률 분포 -> 지수
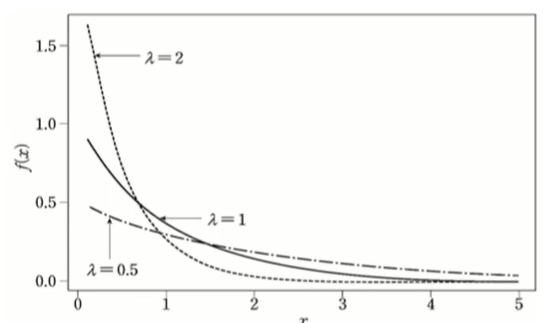
지수 분포 exponential distribution
- 수명에 대한 확률 분포

- 람다가 작아질수록 평균수명이 길어짐.
예제
- exp(3) 을 따르는 지수분포에서 x<1일 확률

- 어느 지역에서 교통사고가 평균 5시간 간격으로 발생. 다음 사고가 5시간 이후 발생 할 확률?
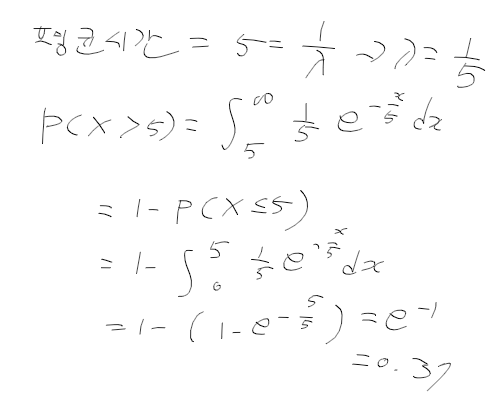
정규 분포 normal distribution
- 일반적으로 사용되는 확률 분포로 기대값을 중심으로 좌우 대칭인 확률 분포

확률 분포 대강 정리?

균등분포 : 모든 확률이 동일한 분포
배르누이 분포 : 한 사건이 서로 배반인 사건에 대한 분포
이항 분포 : 배르누이 시행을 독립적으로 n번했을때 성공한 경우에 대한 확률분포
초기하분포 : 모집단 크기가 N에서 표본 n개를 비복원 추출한 경우에 대한 확률 분포
포아송분포 : 일정기간동안 시행횟수가 크나 발생할 확률이 극히 적은 경우에 대한 확률분포
지수분포 : 사건 발생 사이 시간(수명)에 대한 확률 분포
정규분포 : 기댓값을 중심으로 분포한 확률분포
다변량 확률 분포
- 결합 확률 분포 joint probability distribution : 두개이상의 확률 변수로 이루어진 확률분포
- 주변 확률 분포 marginalized probability distribution : 결합 확률 분포를 구성하는 확률 변수에 대학 확률분포
- 공분산 covariance : 두 확률 변수간 선형관계성을 나타내는 지표
- 상관계수 correlation : 공분산을 표준편차로 나누어 표준화한것
- 다변량 정규분포 : 다변수로 이루어진 정규분포
- 다항분포 ; 다변수 이행분포
결합 분포
- 두 개이상의 확률 분포로 이루어진 확률 분포
ex. 키와 몸무게의 관계?
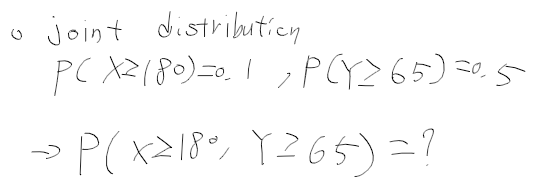
결합확률질량 함수와 주변 확률 분포
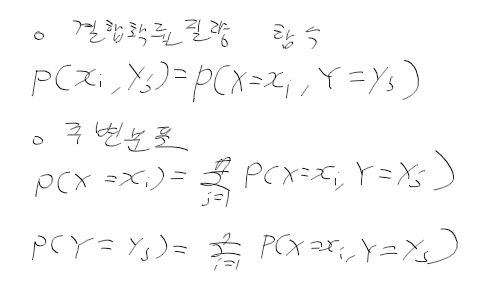
결합확률밀도 함수와 주변 확률 분포

공분산 covariance
- 두 변수간의 선형적 관계
- Cov(X, Y) = E([X - E(X)][y-E(Y)]) = E(XY) - E(X)E(Y)

공분산 계산

공분산 특성
- Cov(X, 상수 a) = 0
- 두 확률 변수 X, Y가 독립 -> Cov(X, Y) = 0
상관 계수 Correlation
- 두 변수간 선형 관계를 나타내는 공분산을 두 변수의 표준편차로 나누어 표준화 시킨것
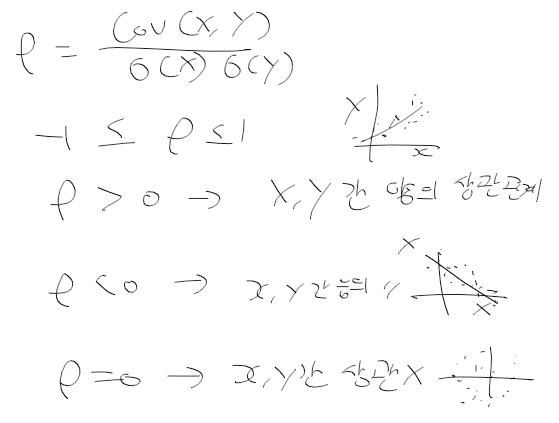
조건부 분포?
- Y값이 주어질떄 X에 대한 확률 분포

정규분포

통계량과 관련된 분포 -> 표본 분포
통계 관련 용어
- 모집단 population : 알고자 하는 전체 집단
- 표본 sample : 모집단에서 추출한 일부분. 모집단을 잘 나타낼수있도록 임의로 잘 추출되어야 한다.
- 표본 분포 sample distribution : 표본들로 이루어진 확률 분포
- 대수의 법칙 : 표본의 수가 많아질수록 표본 평균이 모집단의 평균, 실제 평균에 수렴함.
- t 분포 : 정규 분포를 따르는 모집단의 분산을 모르는 경우 표본 평균의 분포
통계적 추론
- 통계 이론 : 안을 아는상자에서 n개의 공을 임의로 꺼냈을떄 빨간공이 x개 나올 확률?
- 통계 분석 : 안을 모르는 상자에서 n개의 공을 꺼냇을때 x개가 빨간공이라면 상자에서 공은 %나 있을까?
=> 모집단에서 표본을 추출하여 모집단의 통계량을 추정해보자
ex. 국의 맛을 알려면 한숫가락만 마셔도 되지..?
모수와 통계량
- 모수 parameter : 모집단의 특성을 나타내는 미지의 상수
ex) 정규 분포의 평균 mu 과 분산 sigma^2
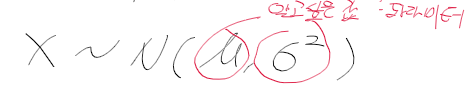
=> 우리는 모집단의 모수를 추정해야한다.
- 통계량 statistic : 모수를 추정하기 위한 표본의 함수
ex) 표본 평균과 표본 분산
=> 표본이 갱신될떄마다 통계량. 즉 표본 평균과 표본 분산은 달라질 수 있다!
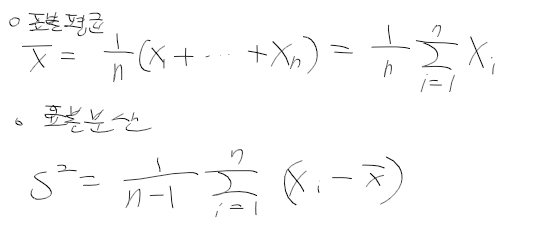
통계적 추론 과정

주사위로 모수 추정하기
- 모집단의 평균과 분산

- 표본 평균과 표본 분산 계산

- 모평균 mu, 분산 sigma^2인 모집단에서 샘플을 임의로 뽑았을떄 표본 평균과 표본 분산

대수의 법칙
- 표본의 수가 클수록 표본평균 bar{X}는 모평균 mu에 수렴
표본 평균의 분포?
- 표본 평균의 분포가 정규분포를 따르지 않는 경우가 많음 => t분포가 나옴
t분포
- X1, X2, ..., Xn이 서로 독립, N(mu, sigma^2)에서 분산을 모를때
- 정규분포를 따르는 정규분포의 분산을 모를떄 => 표본 평균은 t분포를 따른다.
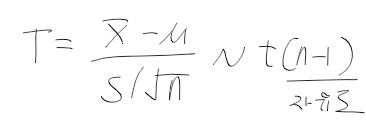
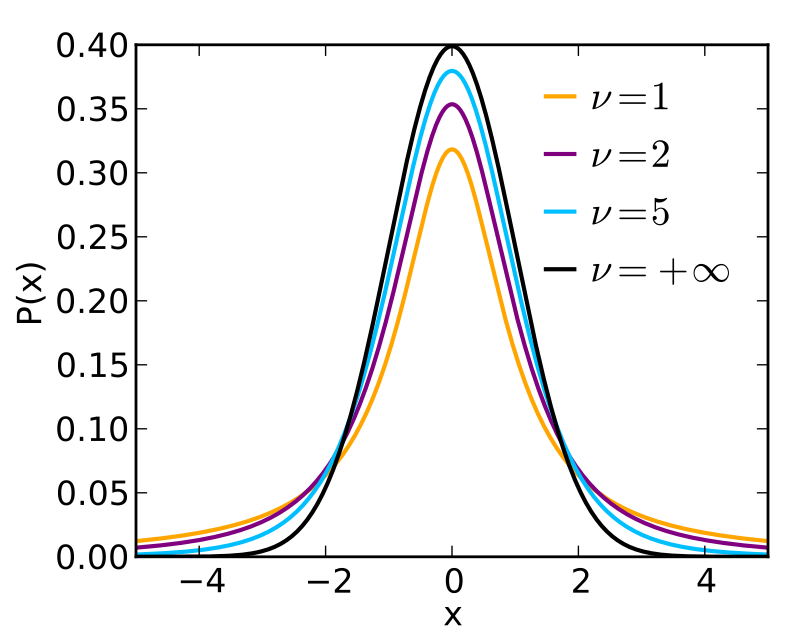
- 자유도가 커질수록 정규 분포에 가까워 진다.
'수학 > 통계' 카테고리의 다른 글
| 데이터분석 - 13. 확률기초 4 (0) | 2020.10.22 |
|---|---|
| 데이터분석 - 12. 확률기초 3 (0) | 2020.10.22 |
| 데이터분석 - 11. 확률기초 (0) | 2020.10.21 |
| 데이터분석 - 10. 다양한 분석 방법과 검정 (0) | 2020.10.21 |
| 데이터분석 - 9. 회귀모형 (0) | 2020.10.21 |