통계량들의 차 비에 대한 분포
극한 분포 - n이 커질떄 어떻게 수렴하는지
표본 평균의 차에 대한 분포
- 다음과 같은 표본이 주어질떄

- 표본 평균은

- 표본 평균의 차를 적률 생성 함수로 구할 수 있음

- sigma1과 sigma2가 동일하다고 가정하면 다음과 같이 표준화하면 표준 정규분포를 따르게됨

공통 분산
- 각각의 분산들을 추정할때 다음과 같이 계산

- X와 Y를 합한 공통 분산을 구하고, 이에 대한 카이제곱 분포는 m+n -2 자유도를 따름

표본 평균의 차에 대한 분포
- 두 집단 모분산을 모르지만 같다고 가정시, m+n - 2의 자유도를 같는 T분포를 따른다
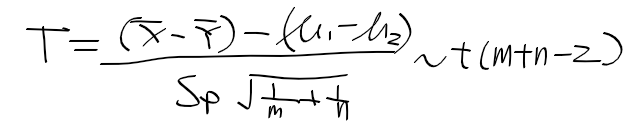
표본 분산 비교
- 표본 분산의 경우 차 보다는 나누어서 주로 비교
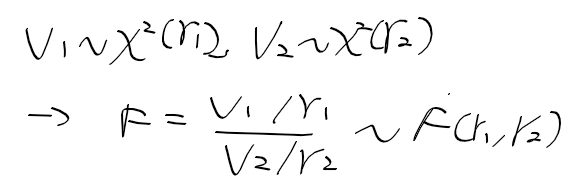
F 분포
- 표본 분산비 : 카이제곱 통계령의 비 -> F분포로 표현됨. 분산분석법에 이용됨
- Fisher를 기르기위해 F분포라 명명

표본 분산의 비교

극한분포
- 표본수가 무한대가 될떄 어떻게 되는지
확률적 수렴
- 모집단이 N(mu, sigma^2)을 따르면, 표본 평균은 N(mu, sigma^2/n)을 따름
- n이 무한이 되면 표본 평균 bar{X}는 mu에 근접(약대수의법칙)

마르코브 부등식
- 약대수 법칙을 증명하기 위해 필요
- 확률변수 X가 주어지고 u(X)가 양의 함수일때 epsilon > 0에 대해 다음이 성립

약대수의 법칙
- X1, ... Xn 이 주어질떄 E(Xi) = mu, 분산 Var(Xi)= sigma^2인 모집단에서 확률 표본일때
- 표본평균 bar{Xn}은 상수 mu에 확률적으로 수렴

예제
- 표본 분산이 확률적으로 모분산에 수렴함을 증명하라

분포로 수렴
- 확률 변수가 하나의 값이 아닌 어떠한 분포로 수렴할수 있음
- 분포의 수렴을 알려면 CDF나 적률생성함수 사용
- 여기서 각 Yi의 누적 분포 함수 Fn(y)에서 n이 무한이 커진 F(y)를 극한 누적 분포 함수 limiting distribution이라 부름.

분포 정리
- 베르누이 분포 : 베르누이 시행에 대한 분포
- 이항 분포 : 베르누이 시행을 n번 한 경우에 대한 분포
- 포아송 분포 : n이 충분히 크고, p가 작고, np가 lambda를 따르는 분포로 사건 발생 횟수에 간한 분포
- 지수분포 : 포아송 분포의 특수한 경우로 사건이 처음 발생할때까지 수명에 관한 분포
- 감마 분포 : gamma 번째 발생할 확률에 대한 분포
- t 분포 : 모분산을 모를때, 표본 분산의 분산을 구하기 위한 분포
- 카이제곱 분포 : 감마분포의 특수한 경우, t분포와 마찬가지로 통계량 추정을 위해 사용
분포 수렴 예제 - n이 무한이 커질때 이항분포가 포아송 분포를 따름을 증명

표본 평균의 분포
1. Xi가 정규분포를 따르는 경우
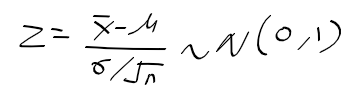
2. 정규 분포를 아니더라도. n이 무한이 커지면 정규분포로 수렴하게 된다.

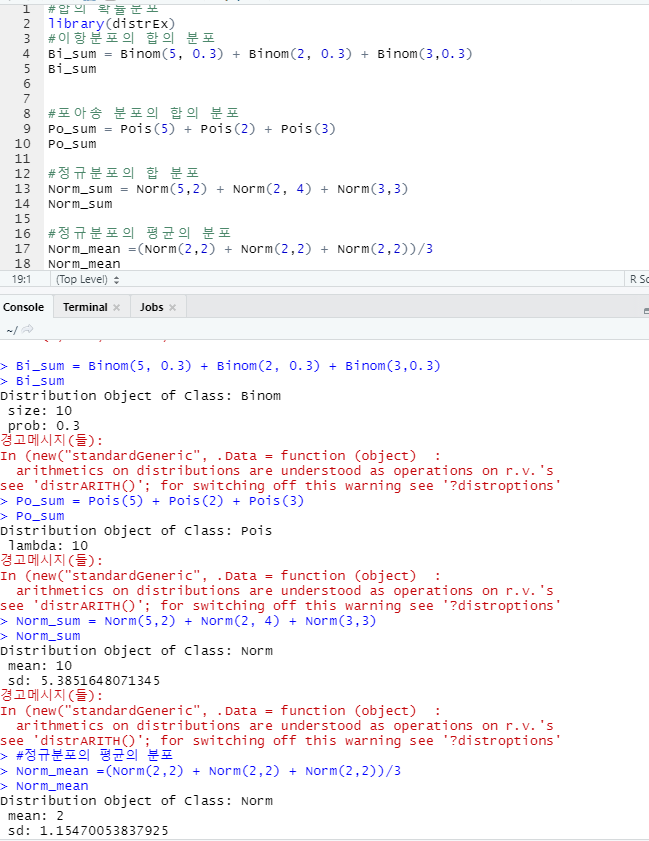
R 실습
1. 정규 분포와 정규분포의 합 분포

2. 이항 분포 합의 분포 , 포아송 분포의 합의 분포, 정규분포 합의 분포, 정규분포 평균의 분포
'수학 > 통계' 카테고리의 다른 글
| 통계 - 8. 점추정량 비교 (0) | 2020.10.26 |
|---|---|
| 통계 - 7. 점추정 (0) | 2020.10.25 |
| 통계 - 5.표본분포 (0) | 2020.10.24 |
| 통계 - 4.연속 확률분포 (0) | 2020.10.24 |
| 통계 - 3.이산 확률 분포 (0) | 2020.10.24 |