모집단
- 우리가 알고자 하는 대상으로 불확실
- 불확실성을 확률, 확률 분포를 이용하여 측정
확률
- 확률 실험으로 나오는 일정한 비율(빈도론)을 확률 이해하기 시작
ex. 동전 던지기, 주사위 던지기 등
표본공간 sample space의 예시
- 자동차 수명
- 동전 던지기 실험
-> 확률 실험으로 구할수 있는 모든 케이스

사건
- 표본 공간의 부분집합
조건부 확률
- 사건 B가 발생한다고 가정할떄 A가 발생할 확률
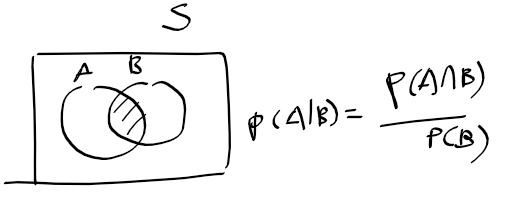
조건부 확률 예시
- 주사위 눈이 짝수(A)가 나왔을때 3이하 수(B)가 나올 확률
S = {1, 2, 3, 4, 5, 6}
A = {2, 4, 6}
B = {1, 2, 3}
A 교 B = {2}
-> P(B|A) = 1/3
역확률 inverse probability
- P(A|B)를 P(B|A)로 바꿔주는것
베이즈 정리
- 표본 공간 B1, .. Bk로 나누고, A 발생을 가정할떄 Bi에 대한 조건부 확률
- "원인 B -> 결과 A"에서 "결과 A -> 원인 B"
배반
- 교사건이 존재하지 않는것
- 사건 A와 사건 B가 동시에 일어날 일이 없는 경우
독립
- 교사건과 각 사건의 곱이 같은것
- 사건 A와 사건 B에 서로 영향을 주지 않음
P(A 교 B) = P(A) P(B)
독립 예제
- 500원 동전, 100원 동전을 던질때 사건 A, B가 독립인지 보자
* A: 500원이 앞면, B: 100원이 앞면
S = {HH, HT, TH, TT}
A = {HH, HT} -> P(A) = 1/2
B = {HH,TH} -> P(B) = 1/2
교사건 = HH -> P(교) = 1/4
=> P(A) P(B) = 1/4 = P(교)
사건 A와 B는 독립
확률 변수 random variable
- 사건을 숫자로 변환해주는 함수
- 표본 공간을 정의역, 실수를 공역으로 하는 함수

확률 질량 함수
- 이산 확률변수 X의 분포
- f(x) = P(X = x), x = 0, 1, 2, ...
확률 밀도 함수
- 연속 확률 변수 X의 분포
- f(x) = d/dx F(x)
기대값 E(X)
- 확률 분포의 무게 중심
분산
- 모집단이 중심(기대값)으로부터 흩어진 정도)
결합 확률 분포 joint probability distribution
- 여러 가지의 확률 변수가 동시에 관측
=> 여러 확률 변수에 대한 결합 확률 밀도/질량 함수로 파악
결합 확률 질량/밀도 함수
- f(x, y) = P(X = x, Y = y)

주변 확률 질량/밀도 함수 marginal probability mass/density function

주변확률밀도함수 예시
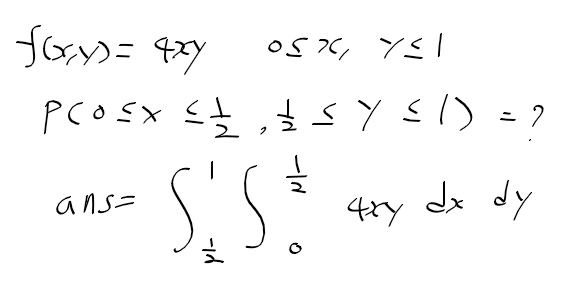
기대값 성질
- E(aX + bY) = aE(X) + bE(Y)
- E(X1 + X2 + .. Xn) = E(X1) + . . . + E(Xn)
한개의 확률 변수를 다룰때
무게중심 기대값과 모집합이 퍼진 정도인 분산에 관심을 가짐
하지만 두개 이상의 변수인 경우
두 변수 간의 관계에 관심을 가져야 함
공분산 Covariance
- 두 확률 변수가 선형적으로 같이 변하는 정도의 측도
Cov(X, Y) = E([X - E(X)] [Y - E(Y)] )
= E(XY) - E(X) E(Y)
상관관계 Correlation
- X의 단위는 명, Y의 단위는 kg 인 경우 공분산 값은 명 kg이 됨 => 표준화가 필요
- 표준화된 두 변수간 선형관계 척도

공분산 구하기 예제
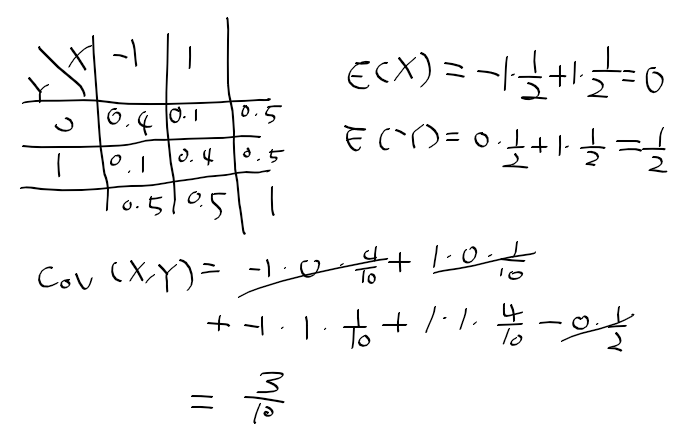
X, Y가 독립 인 경우
- Cov(X, Y) = 0, Corr(X, Y) = 0
적률 Moment 생성함수
- E(X^K)승과 관련있는것을 만들어줌
- E(X)와 관련 있는것 -> 기대값
- E(X^2)와 관련 있는것 ->분산
- E(X^3) -> 왜도
- E(X^4) -> 첨도
=> 적률 : 기대값, 분산, 왜도, 첨도과 같은 것들
적률 생성 함수
- 모집단의 적률을 생성하는 함수
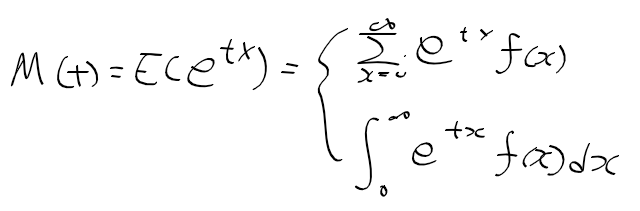
적률
- 확률 변수 X의 k승에 대한 기대값.
- 적률 생성함수를 k승 미분하고 t를 0으로 하면 구할 수 있다.

적률 예제 1

적률 예제 2 - X의 적률 생성 함수와, 1차 적률인 기대값

조건부 확률 밀도함수의 정의

'수학 > 통계' 카테고리의 다른 글
| 통계 - 4.연속 확률분포 (0) | 2020.10.24 |
|---|---|
| 통계 - 3.이산 확률 분포 (0) | 2020.10.24 |
| 통계 - 1. 통계 개요 (0) | 2020.10.23 |
| 데이터분석 - 13. 확률기초 4 (0) | 2020.10.22 |
| 데이터분석 - 12. 확률기초 3 (0) | 2020.10.22 |