집밖은 위험해

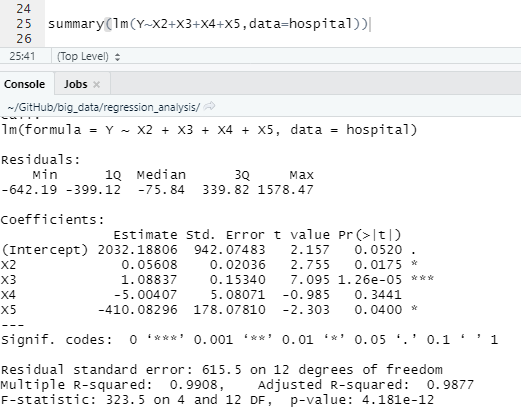
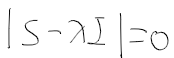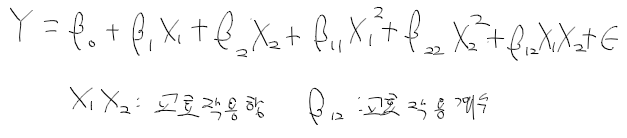19세기 과학자들의 통계적 추론에 대한 생각

- 뉴턴의 방정식 처럼 수학 방정식으로 설명가능하다고 생각

 * 라플라스의 경우 모든것을 알면 과거, 현재, 미래를 설명 및 예측가능하다고 봄.

=> 관측할 때마다 방정식대로 결과가 나오지 않음. -> 관측 오차라 생각.

- 관측 성능이 좋아져도 오차가 제거되지 않음.

현대 물리학 관점

- 방정식이나 기계같지 않고 불확실함.

불확실한 세상 파악방법

- 세상이 확률 분포를 따른다 가정하고, 측정 -> 측정 결과 = 데이터

통계적 추론 statistics inference

- 불확실한 세상을 데이터 기반 추론

- 활용 범위 : 여론 조사, 이미지 인식, 문자 인식, 상품 추천 ㅡㅇ

통계적 추론의 기본 가정

- 세상은 불확실함. 불확실성을 가능성, 확률로 표현

- 세상을 완전히 알수 없음

통계적 추론 원리

- 가장 가능성 높은 결론을 구하자

- 가능성이 낮은 일은 믿지 말자

통계학 정의

- 켄들, 스튜어트 : 자연현상의 성질 측정 데이터를 다룸

- 밀러 : 데이터가 갖는 정보를 이해하는 방법

- 키핑 : 예측 불가능한 변동하는 변수를 다루는 학문

- 체르노프 : 불확실한 상호아서 의사 결정

통계학 정의 정리

1. 관심 대상에 대한 데이터 수집

2. 데이터 요약 정리

3. 불확실한 사실에 대한 결론을 이끌어내는 방법

통계 관련 용어 정리

- 모집단 : 관심 대상 전체 집단

- 표본 : 관심 대상 일부

- 확률 : 사건 발생 가능성

- 확률 분포 : 모집단, 표본을 나타내며 몇개의 모수 parameter로 나타냄.

- 확률 변수 : 관심 변수. 표본 공간의 사건을 숫자로 바꿔주는 함수.

- 통계량 statistic : 표본에 대한 함수 ex. 표본평균, 표본분산

- 표본 분포 : 표본이 확률 변수이므로, 표본에 대한 통계량도 확률 변수. 통계량에 대한 분포

- 통게적 추론 : 통계량으로 모집단의 모수 추정 혹은 검증하기 위한 이론과 방법

통계적 추론과 현실

- 통계적 추론방법은 사고 실험을통해 정립

- 실제 데이터 분석은 이론과는 맞지 않은 문제

- 모집단은 알수 없고, 관측값과 사전 정보만을 알음. 이걸로 모집단에 대해 의사결정 수행

추론이란?

- 알고 있는 것으로 결론을 도출하는 방법

- 연역적 추론 : 이미 있는 결론으로 새 결론 유도

- 귀납적 추론 : 다수 관측으로 결론 유도

- 통계적 추론 : 표본을 이용하여 모집단에 대한 결론을 구하는 귀납적 추론 방법

=> 표본의 정보(통계량)으로 모집단에 대한 모수 추정. 불완정성을 확률로 표현

통계적 추론의 단계

1. 추정 :  표본으로 모집단에 대한 결론 도출

2. 검정 : 모집단 관련 주장에 대한 타당성 점검 => 표본의 정보가 우연인지, 모집단에 존재하는것인지 검토

통계적 추론에 필요한 이론

- 확률 이론 : 모집단/표본 통계량은 어떤 분포를 따르는가. 모집단 가정하에 표본이 어떻게 분포하는가.

- 추론 이론 : 표본으로 모집단을 어떻게 추정해야 타당한지에 대한 이론.

통계적 추론 과정

- 모집단은 모수 theta를 따르는 확률 분포를 따름.

- 확률 분포는 확률 변수의 점확률(pmf, pdf f(x|theta))이 됨.

     * X ~ N(mu, sigma2)로 가정

- bar{x}는 모평균 mu를 추정하기 위한 통계량.

    -> 표본수가 큰경우. 중심극한정리를 따라 근사적으로 정규분포 따름

    -> 표본수가 작을시. 표준화된 bar{x}는 t분포 따름.

- 추정에 필요한 통계량 -> 추론의 원리 이해 필요

  ex. 가능도 원리, 충분성 원리

  * 가능도 원리 liklihood principle : 표본의 joint pdf가 가능도 함수로 표본의 모수를 가지는 원리

  * 충분성 원리 sufficiency principle : 표본을 요약한 통계량이 모수 정보를 안 잃으면 충분성을 가짐.

  => 추정 통계량은 충분 통계량 기반으로 설계.

- 추정량의 유용성 : 평균제곱오차를 최소화 하는 통계량이 유용하다고 봄.  것으로 모집단 모수 추정

    * 평균 제곱 오차 : 손실함수(모수 - 추정량)의 기대값

- 검정 : 확률 표본으로 새로운 가설(대립가설)이 타당한지 보는 방법.

   -> 귀무가설 통계량 도출. 통계량이 가정에 대해 극단적인 값을 가질 시 가정은 기각

  => p value(한계 유의 기준, 유의확률)이 alpha(유의기준)보다 작은 경우 귀무가설 기각. 대립가설 채택

- 최적 검정 : 1종 오류 기준 하에 2종 오류를 최소화

  * 제 1종 오류 : 귀무 가설이 참이나 기각되는오류

  * 제 2종 오류 : 대립 가서이 참이나 기각되는 오류

통계적 추론 관점에 따른 분류

- 빈도론자 frequentist와 베이지안 baysian에 의한 추론으로 분류

- 빈도론자 : 모수를 표본에 대한 통계량의 표본분포 기반으로 추정, 검정

- 베이지안. 베이즈 주이자 : 주어진 데이터와 모수의 사전 확률 기반으로 사후 확률 계산

빈도론자 vs 베이지안

- 베이지안 : 사전 분포에 의존하여 결과가 일정치 않고 계산시간, 비용이 큼

- 빈도론자 : 추정 방법, 통계량에 따라 결과가 일정치 않음 + 주어진 정보 활용 x

현대 통계적 추론

- 어떻게 주어진 데이터로 공정하게 추측할까

- 통계학자가 할일 : 불확실성을 구조화하고 계산하는 것.

- 빈도적, 베이지안 방법을 종합하여 활용해야함.

통계적 추론 역사

- 20세기 전 : 가우스와 라플라스 식으로 데이터 요약

- 20세기 초 : 적은 수의 데이터를 확률 모형으로 만들어 분석, 추론 시작

 *** 칼 피어슨, 이곤 피어슨, 피셔, 고셋, 네이만 ***

- 1901 : 칼피어슨의 적합성 검정 논문 chi-square 검정

    * 칼 피어슨

    - 표본 자체가 확률 분포를 가진다고 봄 -> 모수 측정 불가. 측정값 산포로 유추.

    - 관측 현상은 임의적인것, 확률 분포가 존재

    - 평균, 분산, 왜도, 첨도로 확률 분포 파악 가능.

    - 카이 제곱 검정 : 관측 값을 범주들로 분류, 해당 범주 관측값 수와 이론 분포에 나오는 기대 관측 수 차이 이용.

                        => 유의성 검정에서 활용

- 1908 : 고셋의 평균에 대한 오차(t 분포: 적은 데이터 기반 검정, 추정에서 사용하는 분포)

   => 표본이 작은 경우 표본 평균이 어떤 분포를 따르는가 연구    -> 스튜던트 t의 분포.

- 이후 칼 피어슨의 업적

  1. 가능도 함수와 최대 가능도 추정법 제시.

  2. 유의성 검정 제안.

  3. 랜덤화와 분산분석으로 실험 계획 연구 -> F분포와 F검정 고안

- 네이만과 이곤 피어슨 : 유의성 검정 방법 제안

     1. 귀무 가설, 대립가설 구분

     2. 검정 행위 채택, 기각 구분

     3. 최적 검정이론 연구

- 1930년대 네이만 : 신뢰구간(모수 점추정에 대해 변동성이 필요하다고 봄) 제시

- 1930년대 호텔링 : 다변량 분석

- 1977년 튜키 : 탐색적 데이터 분석

주성분 분석 primary componant analysis 개요

- 연구시 변수 측정. 변수가 100개 존재한다면 너무 많고 어려움

- 정보를 유지하면서 소수의 변수를 이용하여 분석. 

- 어떻게 주성분을 만들고 분석하는가를 다룸

변이 variation

- 정보의 크기

- 일변량 시 분산으로 표현

- 다변량시 서로 다른 변수간 공분산 추가

주성분 principal component

- 다변량 자료가 가지고 있는 총변이의 주요 부분을 가지고 있는 성분

주성분 분석

- 변수들의 정보를 최대한 보존하는 작은 수의 변수들(주성분)을 생성.

- 주성분 분석의 범위 : 주성분 도출 방법과 생성된 주성분 성격과 통계적 추론을 포함

회귀 분석과 관련 예시

- 회귀 분석 모형에서 설명 변수 p가 50인 경우. -> 설명변수, 독립변수가 너무많으면 해석하기 힘듬

- 해결방법

 1. 변수 선택 방법 등 의미있는 변수들 선택하여 회귀모형을 적합

 2. 선형 결합으로 몇개의 새로운 의미있는 변수들을 만들어 회귀분석 실시

-> 세 주성분 Z1, Z2, Z3을 이용한 회귀식

 => 반응 변수, 종속변수 Y를 설명하는데 별 차이가 없다고 할 수 있음.

 -> 차이가 없으면 보다 간편하니 좋은 모형임.

 -> p개의 설명변수 X와 동등한 효과를 같는 적은 수의 새로운 설명변수 Z를 어떻게 만들까

주성분 분석의 목적

- 여러개의 구조적 해석이 힘들며, 서로 상관관계를같는 변수들을 적절히 선형변환 시킴

 => 적은 수의 의미있는, 독립적인 주성분 유도하여 해석하기 위함.

- 다변량 변수들의 단순화, 내적 구조 분석

- 원래 변수들을 선형 결합 형식으로  주성분(서로 상관되지않은, 독립적인) 인공 변수 유도

- 각 주성분이 가지는 변이(정보)의 크기(주성분 분산)을 기준으로 중요도 순서고려

 => 먼저 구한 주성분들이 총 변이(총정보)의 상당부분을 보유하도록 하여 차원 축약

주성분 분석의 역사

- p차원 공간에 흐트러져있는 점들을 직교최소제곱 orthogonal least square 개념에 잘 적합시키는 평면을 찾기위한 기하학 최적화 문제로서 피어슨이 제기

- 호텔링은 변수간 상관구조 분석을 위해 p개의 원래 변수들의 변이를 결정하는데 더 낮은 차원의 독립적 요인을 구하여 성분이라고 함.

* 원래 변수들이 가진 총변이에 대한 각 성분 공헌도를 순차적으로 최대화 하도록 선택된 성분들을 유도하여 이용한 분석이 '주성분 분석'임.

주성분 분석의 활용

- 인자분석, 회귀 분석과 같이 일/다변량 통계적 분석 기법들과 관련을 가짐

- 차원 축약의 결과로 얻은 각 관찰개체별 주성분 점수 principal component score들은 다음 단계 통계 분석(ex. 군집분석, 회귀분석 등)에서 입력자료로 사용됨.

 => 주성분 분석은 분석 과정에서 중간 단계로 사용.

주성분 분석 모형

분산의 공분산 행렬과 상관계수 행렬

- 변수 X1, X2 평균

- 변수 X1, X2의 분산과 공분산

- 상관계수

- 공분산 행렬, 상관계수 행렬

주성분 구하기

- 자료 X를 이용한 주성분 분석은 변수의 분산 공분산 행렬 S나 상관계수 행렬 R로 실시

 * 정보의 크기 = 분산의 크기

- 분산 공분산행렬 S로 주성분 구하기

 1. 고유값(고유근)구하기 : 위 자료의 공분산 행렬 S는 7x7행렬로 7개의 고유값과 고유벡터 쌍을 가짐

- 고유 백터의 크기가 다음과 같을때

- 고유값은 아래의 행렬식을 만족하며, 고유벡터는 고유값에 대응

 => 주성분 분석에서 구하고자 하는 새 변수들은 7개의 고유 벡터들로 구함

 2. 고유벡터 선형변환 : 고유 벡터들을 다음과 같이 직교화 orthogonalization

 - 각 고유벡터의 내적이 1이고, 두벡터의 곱이 0이 되도록 고유벡터들을 선형 변환

 => 각 고유값에 대응하는 고유벡터들을 직교화시 새로운 변수, 주성분 PC1, ..., PC7를 다음과 같이 정의

 => 7개의 변수로 7개의 주성분을 만들었으나, 앞의 일부 주성분 만으로 분석을 해나갈 수 있다.

주성분 가중계수 벡터

- 위 고유벡터 a1, ..., a7를 주성분 가중계수벡터라 부름. 

 => 주성분 의미를 해석하는데 사용됨.

주상분 가중 계수 벡터의 예시

- 아래는 학생들의 다섯 과목 시험 점수에 대한 표본 공분산 행렬 S

 *C1 : 기술, C2 : 벡터 => closed book 시험

* O3 : 대수학, O4: 해석학, O5: 통계학 => open book 시험

- 주성분 결과

- 해석

 Y1은 모든 변수에 대해서 비슷한 양의 가중 계수를 가지므로 첫 주성분은 가중 평균의 의미를 가짐.

 Y2는 closed book 시험에는 양의 가중치, open book 시험에는 음의 가중치를 가지므로 두번째 주성분에서는 클로즈드 북 시험과 오픈북 시험 과목 점수들 사이 대조 관계를 보임

* 개인적 생각 : 클로즈드북 시험인 경우 시험 점수의 분포가 다양하나 오픈 북 시험은 대부분의 학생들의 점수가 비슷하게 잘 나왔기 때문에 이렇다고 보임. 기술 C1이 벡터 C2보다 변동이 큰것 같음.

각 주성분들의 분산과 공분산

- 각 주성분을 정의하는데 이용된 고유벡터들과 쌍을 이루는 고유근이 분산 크기.

 => 고유값 = 분산크기

두 주성분 사이의 공분산

- 주성분들사이 공분산은 0으로 독립임

* PC1은 제 1 주성분, PC2는 제2 주성분 이라고 부름.

양의 상관계수 갖는 이변량 정규분포를 따르는 두변수에서의 주성분

- 분산이 큰 방향이 제 1주성분, 분산이 작은 부분이 제2주성분임.

표본 상관 행렬을 이용한 주성분 분석

- 주성분 분석시 표본 상관 행렬을 많이 사용한다고함

 * 변수를 표준화, 즉 측정단위에 얽매이지 않게됨.

- 주성분 분석은 표본 공분산 행렬 S의 고유값과 고유벡터를 이용하여 분산 중심 분석법.

 -> 여기서 변수 분산이 1이 되도록 변수를 표준 편차로 나눔

- 표준화 후 표준화 변수 벡터 Z에 대해 분산은 1, 공분산은 상관계수가 됨.

상관계수행렬 R에 기초한 주성분

- 표본 공분산 행렬 S로부터 주성분의 기본적 성질을 그대로 유지

- 주성분 분석에서 S와 R 중 어느 행렬을 분석대상으로 하느냐에 따라 주성분이 서로 다르게 됨.

 => 원래 변수들의 선형 결합인 주성분이 의미를 가지려면 적어도 모든 변수가 동일한 단위로 측정되 필요 있음.

 * 아래의 경우(주성분의 의미가 애매해지는)를 방지하기 위함.

- 고려대상의 변수가 직접 비교될 수 없는 단위로 측정된 경우, 각 변수를 표준화 시켜 주성분을 행함. 주성분 분석을 상관행렬에 기초하여 수행. 표준화 변수에 기초한 표준 상관행렬 R을 사용하는 경우 모든 변수의 분산이 똑같이 1이 되어 각 변수가 가지는 변이에서의 상대적 차이 무시

- 사회과학에서 변수는 측정단위가 자의적인 경우가 많음

-> 개별변수 변의 차이에 의미를 부여하는게 힘들 수 있음

 => 상관계수 행렬 R에 기초한 주성분이 많이 사용

주성분 분석 목적

- 기존의 p개의 변수 벡터 X에서 변이(정보)를 잃지 않는 한 작은 수의 주성분유도

 => 차원 축소와 자료 요약

주성분의 특성

1. 7개의 변수 X1, X2, ..., X7의 상관계수 r12, r23, ...., r67이 모두 1인경우 

 => 7개의 변수는 하나의 변수, 즉 주성분 1개로 대표 할 수 있다.

 * 고유값 lambda 1을 제외한 나머지는 0

2, 7개의 변수 중 한 변수(X7)가 나머지 6개의 변수들의 선형 결합으로 만들어 지는 경우

주성분의 중요도

- 주성분 PC1 : 가장 중요한 주성분 변수로, 변수가 7개시 PC1의 중요도는 아래와 같음.

1988년 서울 올림픽 육상 여성 7종 경기 결과에 대한 주성분 분석

1. 자료 준비

2. 자료 변환

- hurdles, run200m, run800m은 값이 작을수록 좋으므로 변형

 => 높은 점수가 좋은 점수가 되도록 최대값에서 빼줌

3. 주성분 분석 실행

- stats 라이브러리의 princomp 함수 사용

- 변수가 7개이므로, 7개의 주성분을 구하고, 각 주성분의 표준 편차 출력

4. 주성분 분석 결과

- 첫 주성분이 63.72%, 두번째 주성분이 17.06%로 두 주성분이 총 변량 80.8%정보 차지

- 각 주성분의 표준편차를 제곱하여 고유값을 구할 수 있음.

- 제 3 주성분의 고유값이 0.5로 유의미한 주성분은 2개

---- 후기 ---

이전에 주성분 분석에 대한 이야기를 처음 들었을때가 

패턴 인식을 공부했을 때였다.

그 때 피처가 큰 경우 차원수를 줄일수 있도록 하기 위해 주성분 분석법을 사용한다고 설명되어 있었지만

컴퓨터 과학적 관점에서 주성분 분석을 다루어서 인지

주성분 분석을 왜하는 것인가.

주성분 분석을 하는 방법 정도는 적혀 있었던것 같은데

내가 그 당시 기반 지식이 부족해서인지는 잘 모르겟으나

뭔가 말은 이해는 가는데 조금 부족하다는 생각이 들더라

지금 통계과에서 주성분 분석에 대해 들으니

조금은 당시 부족했던 부분들이 이해가기 시작한다.

컴퓨터 과학에서 다루는 주성분 분석은 계산을 더 효율적으로 하기 위하다보니

변수 간에 어떤 관계가 존재하는지 설명하는 부분이 어려웠던것 같았다.

지금 수업을 들으면서 사회 과학에서 주성분 분석 시 변수 들간의 의미를 

주성분 분석을 통해 이렇게 축약할수 있는가

조금 더 명확하게 이해되면서

공부하면서 스토리 텔링이 참 중요한것 같다.

단변량 데이터 다루기

1. 데이터 읽고 기술통계량 보기

 다변량 분석

주성분 분석, 인자 분석, 분산분석 등 두 개 이상의 변수들의 관계를 분석하는 모든 통계적 기법

 c(a: b)

- a에서 b까지 수 벡터 생성

%/%

- 나누기 연산

%%

- 몫 연산

seq(a, b, length = x)

- a ~ b 사이 10개 간격으로 값 생성

rnorm()

- 난수 생성

- 정규 분포를 따름

ex.1 평균이 10이고, 표준편차가 1인 정규분포를 따르는 난수 10개 생성시

 => rnorm(10, 10, 1)

행렬 생성 

- matrix(수열, ncols= 값, byrow=T/F)

- matrix(1, nrow=x, ncol=y)

모든 값이 1인 x y 행렬 생성

서브 행렬 추출

- x가 행렬인 경우

- x[, c(1:3)] : 1 ~ 3열까지 모든 행데이터 추출

전치행렬

- t(행렬)

전치 행렬과 행렬의 곱

- %*%

함수 작성

square = function(x) {x *x}

sqaure(4)

패키지 설치 및 로드

산점도와 상관계수 예시

-  학생 10명의 수학, 물리 점수 사이 상관관계 보기

- 산점도 그리고, 상관계수 보자

- 상관계수는 0.9921232로 수학과 물리 점수사이 강한 선형적 상관관계가 있음을 알 수 있음.

기술 통계량 descriptive statistics 구하기

- 기술통계량 : 통계 데이터를 나타내는 대표적인 통계량들. 평균, 분산, 사분위수, 표준편차, 중앙값 등

엑셀 데이터 읽기

- library(xlsx)

- read.xlsx("경로", 1)

 * 여기서 1은 sheet 넘버가 1을 의미

데이터 일부 출력

- head() : 맨위 데이터 일부 출력

기술 통계량 출력

- summary(데이터 프레임) : 변수 그룹별, 평균와4분위수 등 출력

attach(데이터 프레임)

- 데이터 프레임 이름 선언 없이 변수에 접근 가능한 함수

- 이 함수를 사용안하면 데이터프레임$변수명 으로 접근해야함

그룹별 기술 통계량 출력하기

- tapply(기술통계량 구할 값들,그룹,기술통계량)

두 그룹에 대한 기술 통계량을 보고 싶은 경우

- list(그룹 변수1, 그룹 변수2) : 두 그룹에 대한 경우들을 만듬

- table(변수) : 분빈도 보기

두 빈도 변수, 분할표에 대해서 독립성 검증 하기

-> 카이제곱 통계량을 구함.

1. 두 변수에 대한 분할표 작성

2. summary(분할표) 호출

=>  카이제곱 통계량, 자유도, pval(유의 확률, 한계유의기준)을 알수 있음.

성별과 교육 수준에 따른 월 수입 분석

1. 데이터 읽고, 도수 분포표 만들기

2. 교육 별 도수분포표 막대 그림

3. 나이와 월수입에 대한 산점도 그리기

4. 남녀 구별 : 나이와 월 수입에 대한 산점도 그리기

독립변수가 4개인 데이터 회귀 분석

1. 데이터 로드, 회귀 모형 적합

- lsfit(x, y) 함수 

2. 잔차와 예측치에 대한 산점도 그리기

기존의 회귀 모형 regression model

- 기본 가정 : 오차 등분산성, 모형의 선형성, 오차의 정규성

반응 변수 Y가 정규 분포가 아닌경우

- 오차의 등분산성 위배 -> 분산안정화변화로 해결

- 오차의 정규성이 위배(오차가 정규분포를 안따를떄) : 일반화 선형 모형

일반화 선형 모형를 사용하는 경우

- 반응변수 Y가 정규분포를 안따르는 경우

 ex. 반응변수가 비율을 나타내는 경우, 반응변수가 양의 개수를 나타내는 포아송 분포를 따르는 경우

일반화 선형 모형 generalized linear model

- 반응 분포가 정규 분포 뿐만아니라, 이항분포, 포아송분포,

  감마 분포와 같은 지수족 분포를 따를때 회귀 모형 형태로 확장된 모형

* 회귀모형의 한계를 극복함.

일반화 선형 모형의 구성성분 세가지

- 반응 변수의 분포

- 선형 예측자 eta = beta_0 + beta_1 X = g(mu)

- 연결 함수 g(mu) = log(mu)

예시 : 1983 ~ 1986년 동안 호주에서 에이즈로 인한 사망자수

x : 1983년 1월부터 3개월 단위 경과 기간

y : 사망자수

선형 모형의 일반화 선형 모형으로 확장

지수족 분포 the exponential family of distributon

- 반응변수 분포가 지수족 분포를 따를때 일반화 선형 모형 사용

- 확률 밀도함수 f(y;theta;phi)와 같이 표현되는 분포로 아래와 같음.

- theta : 평균 mu의 함수로 정준 모수 canonical parameter

- phi : y의 분산과 관련되고, 평균과는 독립인 산포모수 dispersion param

- w : y 분포 가정에 따라 사전에 알수있는값

선형 예측차 eta linear predictor 

- 설명변수들의 선형 결합

연결 함수 link function

- 선형 예측자와 반응변수의 평균 사이 관계를 eta가 되도록 만들어주는 함수 g()

지수족 분포의 정준 연결 canonical link

로지스틱 회귀모형

- 반응 변수가 이항 자료인 경우 사용

=> 로지스틱 회귀모형 : 로짓 함수가 선형 연측자가 되는 모형.

ex. 날다람쥐의 출현 자료( 독립 : con_metric ,  p_size_km, 종속: 1 또는 0)

 => y = occur, 1=yes, 0= no => 이항분포를 따름

- 로지스틱 회귀 모형

 -> -3.606 + 0.024 x1 + 1.632 x2

- deviance 이탈도 : 선형 회귀 모형의 잔차 제곱합을 일반화한 개념. 정규분포를 따른다고 한다면 카이제곱 분포를 따름.

로지스틱 회귀 모형의 유의성 검정

- H0 : log (pi/(1-pi) = beta0 vs  H1 : log(pi/(1-pi) = beta0 + beta1x1 + beta2x2

 => 정리하면 H0 : beta1 = 0, beta2 = 0 vs H1: 적어도 하나는 0이 아니다.

- 두 이탈도의 차이가 유의한지 보면됨.

회귀 모형 regression model

- 단순 회귀 모형 : 독립변수와 종속변수간에 선형적 관계를 갖는 경우 사용

- 다항 회귀 모형 : 독립변수와 종속변수간에 비선형적인 관계를 같는 경우

다항 회귀 모형 polynomial regression model

1. 독립변수가 하나인 경우 이차 다항 회귀 모형

2. 독립변수가 2개 인경우 이차다항회귀모형

다항회귀모형 예제 1

1. 데이터 로드, 플롯

- 연도별 교통범죄발생률과 승용차보급률

- 플롯시켰더니 약간 비선형적

 => 2차 다항 회귀모형으로 만들어보자.

* attach(데이터프레임). => plot시 데이터프레임$ 를 생략할수 있음

2. 모형 생성 

- 구한 이차다항회귀모형은 아래와 같다.

다항회귀모형 예제 2 : 1990~1992년까지 마라톤 대회 5km 구간별 평균속도

1. 데이터 로드, 플롯

- 데이터 형태를 보니 3차 다항회귀모형을 만들자

2. 모형 추정

- beta0 ~ 3까지 pvalue가 매우 작음 => 유의

가변수 회귀모형 dummy variable regression model

- 독립변수에 이산형 변수가 포함되어있는 경우에 사용

- 가변수 dummy variable, indicator variable ; 두가지 값을 갖는 변수

- 예시 : 비누 생산공장에서 부스러기양과 공정속도

=> 교호작용을 고려한 모형

=> 교호작용이 없는 모형

R에서 실습

1. 데이터 읽고 산점도 그리기

- line0와 line1은 기울기는 차이없고, 공정에 따라 차이가 있어보임

=> 교호작용이없는 모형을 고려

2. 모델 생성

- 교호작용이 없는 모형

- 두 생산 라인은 beta2만큼의 차이가 존재

 H0 : beta2 = 0을 기각한다면 => 두 생산공정에 차이가 존재

- p value가 매우 작으므로 두 생산 공정에 차이가 존재하며, 차이는 53정도.

- adjust R2는 0.9352로 유의

3. 모델 만들기

- 교호작용을 고려한 경우

- X:Dline1 의 경우 pval이 0.18로 유의수준보다 크므로 유의하지 않음.

 => 교호작용을 고려하지 않은 모형이 적합.

변수 선택과 기준/방법, 다중 공선성

다중 회귀 모형

- 여러개의 독립변수에 의해 종속변수 y에 주는 영향을 함수 식으로 표현한것

변수선택 variable selection problem

- 많은 설명 변수 중에서 모형에 포함시킬 변수를 결정하는 것

다중공선성 multicollinearity

- 모형에 포함되는 설명변수들 사이 연관성이 존재하는 경우 모형의 안정성과 신뢰성을 떨어트림

=> 공선성, 다중공선성

- 두 설명변수 X1, X2가 상수 c0, c1,c2에 대해 다음 관계를 가지는 경우

  -> 두 변수 사이에 완벽한 공선성(exact collinearity)가 있음

ex. X1 + X2 = 100인경우 X2는 X1으로 결정됨

다중공선성 multiconllinearity

- 설명변수가 2개가 넘는 경우 다음과 같은 관계가 성립하거나 근사적으로 성립할시

 => 설명변수들 사이에 다중 공선성 multiconllinearity이 존재

- 설명변수 Xh와 나머지 설명변수간의 결정계수(다중상관계수의제곱) Rh^2이 다중공선성의 정도를 나타냄.

다중 공선성에 대해 의심이 드는 경우

- 설명변수의 표본 상관행렬에서 상관계수가 크게 +-1에 가까울떄

- 설명변수를 모형에 추가/제거시 추정된 회귀계수의 크기나 부호에 큰 변화를 줄때

- 새 자료를 추가/제거시 추정된 회귀 계수의 크기나 부호에 큰 변화를 줄때

- 중요하다고 생각되는 설명변수의 검정 결과가 유의하지 않거나 신뢰구간이 넓을때

- 추정된 회귀 계수의 부호가 과거의 경험이나 이론적인 면에서 기대되는 부호와 상반될때

분산팽창인자 VIF; variance inflaction factor

- R_j^2 : Xj를 반응변수로 보고 나머지 설명변수에 대한 결정 계수

- k개의 VIF_j 중 가장 큰 값이 5~10이 넘으면 다중공선성 있다고 판단.

병원 데이터를 이용한 예제

1. 데이터

Y : 월간 의사 연 근무시간

X1 : 일평균 환자수

X2 : 월간 Xray 초라영 횟수

X3 : 월간 이용병석수

X4 : 해당지역 병원이용가능인구 / 1000

X5 : 평균입원일

2. 회귀모형 구하고 보기

- X1 일평균환자 : 늘어날수록, 근무시간 Y는 늘어날탠대 -15.85167이 나옴

- X4 병원가능인구가 늘어날수록, 근무시간 Y는 늘어나야하나 -4.219가 나옴.

- X5 평균입원일이 늘어날수록, 근무시가이 늘어야하나 -394...

=> 독립변수간에 다중공선성이 존재가 예상되며, 분산 팽창인자 등에 의한 진단이 필요.

3. 분산팽창인자 계산하기

- X1, X2, X3, X4의 분산팽창인자를 계산해보면 5이상으로 다중 공선성 문제가 존재

4. 독립변수간 상관관계 보기

- cor()함수 : 상관계수 행렬

- X5를 제외한 X1 ~ X4까지 강한 선형 상관관계가 존재. x5를 제외하고 대부분 1에 가까움.

설명변수 X1을 제외한 경우 모형을 보자

1. summary

- R2는 차이없음

- 추정된 회귀계수의 표준 오차는 조금 줄어듬

2. 분산팽창지수 보기

- x1이 포함되었을때보다 크게 줄어듬

모형 선택 기준 - 결졍 계수

-  R_p^2는 k개의 설명변수중에서 p개의 설명변수로 구성되는 모형에서 아래처럼 정의

- 결졍 계수는 설명 변수가 추가되어 p가 커질수록 증가

 =>모든 변수가 포함이 다된 모형(p=k)일때 최대되도록 증가

= 최대 결정계수 값인 모형을 선택은 의미 없음.

모형 선택의 기준 - 수정 결정계수 adjusted coefficient of determination

- 결정계수 R_p^2의 문제를 보완하기 위한 방법.

- SS를 그대로 쓰기보다 자유도로 나누어 조정과정을 거침

- bar R_p^2는 설명변수가 증가해도 항상증가하지않음

=> 모형 선택시 수정 결정계수가 큰것을 사용하자

모형 선택 기준 : mallows Cp 통계량, AIC

- k개의 독립변수 중에서 p개의 변수를 선택할때, C_p가 최소가되는 모형을 선택

- AIC : 작은값을 갖는 모형을 선택

변수 선택 방법

- 모든 가능한 회귀 all possible regression

- 앞에서부터 선택 forward selection

- 뒤에서부터 선택  backward elimination

- 단계별 회귀 stepwise regression

1. 모든 가능한 회귀

- 독립변수가 k개 있으면 2^k -1 개의 회귀모형을 다뤄보자

 => k가 커질수록 계산량이 급격히 늘어남

1.1 데이터 로드

- 독립변수 4개,

1.2 모든 가능한 회귀 수행

- leaps 패키지의 regsubsets()함수

- 선택 알고리즘 : exhaustive

- 독립변수가 1개인 경우 가장 좋은 모형은 X4

- 독립변수가 2개인경우 가장 좋은 모형은 X1, X2

- 독립변수가 3개인 경우는 X1, X2, X4

1.4 구체적인 통계량을 보기

- 아래의 통계량을 정리해보면 X1, X2, X4가 사용된경우 조정된 R2가 가장 크고

- X1, X2인 경우 Cp가 가장 작다

- Cp는 작을수록 좋고, 조정된 R2는 클수록 좋다.

=> X1X2 나 X1X2X4 선택

2. 앞에서부터 선택 forward selection method

- k개의 설명변수 중에서 가장 영향이 큰 변수부터 하나씩 선택

- 더이상 중요한 변수가 없다고 판단할때 선택 중단하는 방법

2.1 R에서 실습

- AIC기준으로 수행. AIC는 값이 작을 수록 좋음.

- X3은 없는게 나으므로 X4, X1, X2를 선택

뒤에서부터 제거 backward elimination method

- 모든 독립변수를 사용한 모델에서부터 기여도가 작은 변수를 제거해나가는 방법

단계별 회귀 stepwise selection

- 앞에서 선택법에 뒤에서 제거법을 가미

- 새 변수가 추가될떄마다 기존 변수가 제거 될 필요가 있는지 검토하여 선택

Y~1에서 

+X4하는 경우 AIC

~ +X3하는경우 AIC

=> X4를 추가하는것이 AIC가 가장작다 

Y~X4에서 

+X1하는경우 / +X3하는경우 /  추가 x/ +X2 경우 / -X4 경우

=> +X1일떄 AIC가 가장적다. => X1 추가

...

더하는 경우와 빼는 경우를 동시에 고려

데이터 분석 방법 복습

이산형

- 일원배치법

- 이원배치법

연속형

- 회귀모형

(다)중 회귀모형 multiple regression model

- 종속 변수의 변화를 설명하는데 두 개 이상의 독립 변수가 사용되는 회귀 모형

- 선형인 경우 다중 선형 회귀 모형

독립변수가 k개인 다중 회귀 모형

- beta0, ..., betak : 모집단 회귀 계수

- epsilion i : Yi를 측정시 오차

독립변수가 2개인 다중 회귀 모형

- 벡터로 나타내는 경우

다중 회귀 모형 - 행렬 + 독립변수 2개

상점의 총 판매액 자료를 이용한 다중 회귀 분석

- 독립변수 : 광고료 x1, 상점크기 x2

- 종속변수 : 총 판매액 y

다중 회귀 모델 - 최소제곱법

- 행렬을 이용하면 쉽게 추정치 beta를 구할 수 있다.

- 다중 회귀 모델

- 오차에 대한 식

- 오차 제곱 합에 대해서 정리하면

- beta에 대하여 미분하고, hat beta(estimate beta)를 구한다.

R로 다중 회귀 모델 구하기

- 결과

잔차 residual

- 관측값 Yi - 추정된 회귀값 hat Yi

- 추정값과 잔차 사이의 관계

햇 행렬 hat maixt

- 햇 행렬의 정의

- 다음 성질을 만족하는 멱등행렬 idempotent matrix

회귀 방정식의 신뢰성 보기

- 분산분석표에서 F 검정

- 결정계수

- 잔차 평균 제곱

총 제곱합 SST

잔차제곱합

회귀제곱합

변동 분해

중회귀 분산분석표

- 검정통계량 F0 : 회귀방정식이 유의한가를 검정하기 위한 검정 통계량

- H0 : beta1 = beta2 = ... = 0   vs H1 : 하나의 betai != 0

- 유의수준 alpha에서 F0 > F(k, n-k-1;alpha) 인 경우 귀무가설을 기각 => 회귀방정식이 유의

- R에서 F0에 대한 유의확률 Pvalue가 유의수준 alpha보다 작다면 귀무가설 기각함 

R로 회귀 식 구하기

- 분산분석표로 보기

결정계수 coefficient of determinantion

- 이 회귀 식이 얼마나 설명력이 있는지 나타내는 값 R^2

중 상관계수 mutiple correlation coefficient

- 단순 회귀에서 결정계수 R^2 = 두변수의 상관계수 제곱과 같다. corr ^2

- 중회귀 모델에서 결정계수 = 반응변수 Yi와 추정값 hat Yi의 상관게수의 제곱

=> 다중회귀모델에서 결정계수의 제곱근

예측방법론

- 예측에는 주관적 예측과 객관적 예측이 있음

- 데이터 기반 예측 -> 객관적 예측

- 시계열 특성과 예측 모형을 보고 R 구현

회귀 분석 regression analysis

- 독립변수와 종속변수 사이의 함수 관계(모형)을 구하는 통계적 분석 방법

- 독립 변수 independent variable, 설명변수 explanatory variable: 영향을 주는 변수 x

- 종속변수 dependent variable, 반응변수 response variable : 영향을 받는 변수 y

회귀 용어의 유래

- 영국의 우생할자 galton이, 부모콩의 무게를 x 자식콩이 무게를 y로 산점도를 그려 관계를 살펴봄

 => 자식의 무게는 평균 무게로 회귀(되돌아 가려는)하려는 경향을 발견 => 피어슨이 분석하여 발표

단순 회귀 모형 simple regression model

- 가장 간단한 회귀 모형

- 독립 변수와 종속 변수 사이에 선형적 관계를 표현함

- Yi : i번째 측정된 반응변수 Y의 값

- beta 0 : 절편 회귀계수

- beta 1 : 기울기 회귀계수

- Xi = i번쨰 상수 X값

- epsilon i = i번쨰 측정된 Y의 오차항

회귀선 regression line

- 표본으로 모형식을 추정하여 구한 직선. 추정된 회귀 직선, 회귀선이라 함.

-b0와 b1은 beta0와 beta1의 추정값

- hat{Y}는 E(Y)의 추정값

- b0는 회귀절편 intercept

- b1은 X가 한단계 증가할떄 hat Y의 증가량으로 기울기 slope

- 회귀 계수 b0, b1을 구하는 방법 => 최소제곱법

최소제곱법 method of least square LSM

- 회귀 모델이 다음과 같이 주어질떄

- 오차 항 제곱 합은 아래와 같다.

- > S를 beta0과 beta1에 대해 각각 편미분한 결과가 0이 되는 beta0와 beta1를 b0와 b1로 함.

-위 식을 정리하면 아래와 같으며, 이 식을 정규 방정식 normal equation

- b0와 b1에 대하여 정리

선형 회귀 모델 예제 - 광고료와 총판매액

- 기울기는 2.6087으로 추정 p value가 매우 작으므로, 귀무가설 기각 -> 유의한 결과를 보임

- 절편은 -2.2696으로 추정

잔차 residual

- Xi에서 관측된 값 Yi와 추정된 hat Yi사이 차이

- 잔차의 합은 0

- 잔차의 제곱합은 최소

- 관찰값 Yi의 합과 추정된 hat Yi는 같다.

- R에서 확인하기

회귀 모형의 정도

- 구한 회귀 모형이 얼마나 좋은가?

분산 분석표에 의한 F 검정

- 변동 분해하기

 회귀제곱합의 자유도는 독립변수가 1개이므로 

 총 데이터 수가 n개에서 평균에 대한것을 빼므로 n - 1

 => 잔차제곱합의 자유도는 n - 2

분산분석표를 이용한 F 검정

- 변동을 분해한 표

- 가설 검정

- F0 > F(1, n-2; alpha) 이면 유의수준 alpha에서 귀무가설을 기각 => 회귀 직선이 유의하다

- R에서 유의 확률 p value를 제공. pvalue < alpha이면 귀무가설 기각

R에서 분산분석

- p value가 0.001487로 매우 작으므로 귀무가설을 기각

결정계수 coefficient of determination

- 회귀선이 어느정도의 설명력을 가지고 있는가를 나타내는 지표

- R^2는 0 ~ 1

- X와 Y 사이 높은 상관관계를 가질수록 R^2 는 1에 가까워짐

-> 0에 가까우면 유용성이 떨어지는 회귀선

- 회귀선으로 설명되는 변동/총변동이므로 회귀선의 기여율이라고도함.

추정값의 표준 오차 Mean Squared Error

- 잔차 평균 제곱 MSE는 오차 분산 sigma2의 불편추정량.

- sqrt(MSE)로 표준 오차를 구함

분산분석 -> 요인의 수준이 이산형(100, 120)에 따른 종속변수의 영향

회귀분석 : x가 이산이 아닌 연속인경우 분석 방법

공분산분석 : x가 이산형인것도 있고 연속형인것도 두개다 있는 경우

회귀분석 regression analysis

- 독립변수들과 종속변수 간에 관계를 함수식으로 정리하여 분석하는 방법

- 독립/종속변수는 연속값

- 단순 회귀 simple regression : 독립변수가 하나

- 다중 회귀 multiple regression  :독립변수가 여러개

다중 선형 회귀 multiple linear regression

다항 회귀 모형 polynomial regression model

상관계수 correation coefficient

- 두 변수간에 선형적 상관관계에 대해서 나타냄

- 1에 가까우면 양의 상관관계

- -1에 가까우면 음의 상관관계

- 0에 가까우면 선형적 상관관계가 존재하지 않음

단순 선형 회귀 분석 simple linear regresion analysis

- 모형 model

- 관측치 measurements

- 추정식 estimator

- 잔차 residual

최소제곱법 least squared method LSM

다음 데이터가 주어질떄 단순선형회귀를 수행하라

R로 테스트

- 추정량 -0.28928

- 기울기 0.45664 -> pvalue = 3.21e-07로 매우작다 =>유의하다.

- R-squared : 0.9338로 유의함

회귀선의 유의성 검정

- 두 변수 사이에 회귀 관계가 없다면 beta1는 0이되어 다음의 식이 성립합.

- 총제곱합과 잔차제곱합, 회귀제곱합 사이의 관계

결정계수 coefficient of determination R^2

- 회귀식이 얼마나 의미있는지

- R square가 크면 클수록 유의하다.

- 회귀 계수 beta1의 유의성

 -> H0: 회귀관계가 없다. vs H1 : 회귀관계가 있다.

     H0: beta1 = 0 vs H0: beta1 !=0

분석분석표

- 회귀분석의 유의성 검정

분산분석표 분석

유의확률 pvale가 매우 작으므로 h0 기각. 매우 유의

공분산 분석

- 분산분석 + 회귀분석

- 일원 배치 분산분석 : 기계(3대) -> 섬유 제품 강도

- 이원 배치 분산분석 : 기계(3대), 원사두께(얇음,두꺼움) -> 섬유제품 강도

- 공분산 분석 : 기계(3대), 원사 두께(연속적인값, 공변수 covariate) -> 섬유제품 강도

공분산 분석 예시

- 일원배치 예시 : 두개의 사료 (A,B) => 섭취후 체중 y

- 공분산 분석 예시 : 두 사료(A,B), 초기체중 x(연속적인값) => 섭취후 체중 y