일치성
- 표본 크기가 증가할 수록 추정량의 분포가 모수로 수렴하는 성질
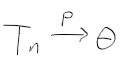
일치 추정량
- Tn = T(X1, ..., Xn) n개의 표본을 사용한 추정량
- {T1, ..., T_inf}는 모수 theta에 대한 점추정량 수열
- Tn을 일치 추정량이라 함.

충분성 sufficiency
- 모수에 대해 더이상 정보를 제공하는 통계량이 없는 경우.
=> 그 추정량은 충분성을 가짐
- 통계량이 표본 모수에 대한 정보를 읽지않고 모수를 추정할 수 있는 성질
- 충분통계량 : 충분성을 같는 통계량
충분 통계량
- theta에 대한 추정량 T에 대해 T가 주어졌을때 X1, X2, ..., Xn의 조건부 분포가 모수 theta에 의존하지 않을때 T
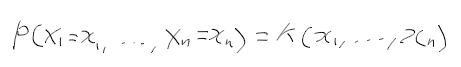
피셔-네이만 인수분해 정리
- 확률 표본 X1, ..., Xn에서 theta의 추정 통계량 T = h(X1, ..., Xn)이 충분 통계량일 필요 충분조건
=> 결합확률밀도함수가 함수 g와 h로 표현되는것.
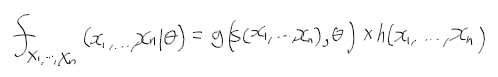
충분 통계량 예제 1
- X1, ..., Xn이 정규분포 N(mu, 1)을 따르는 확률 표본인경우 mu에 대한 충분 통계량 구하기

완비 통계량 complete statistics
- 완비성을 갖는 통계량
- 통계량 함수의 기대값이 모든 모수에서 0인 경우 통계량 함수 값 자체가 0인 통계량
- 충분 통계량이면서 완비 통계량인경우 => 완비충분통계량(complete and sufficient statistic, CSS)
완비 통계량
- 모든 theta와 통계량 T(X)의 함수 g에 대해 아래가 성립하는경우 T(X)
- 모든 theta와 함수 g에 대해 다음이 성립 -> T(X)가 완비통계량

완비통계량 예제
- 확률 표본이 베르누이분포 Ber(P)를 따르는 경우, Sigma Xi가 p에 대한 완비통계량 증명
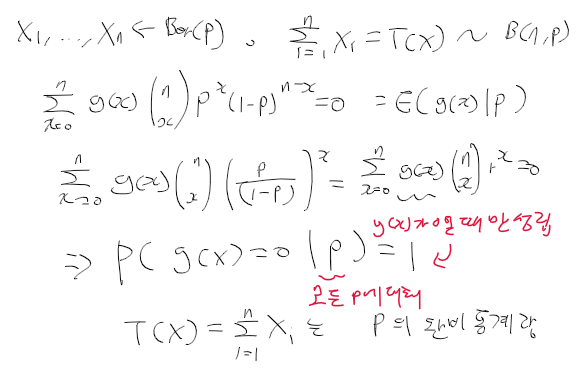
완비 통계량 복습
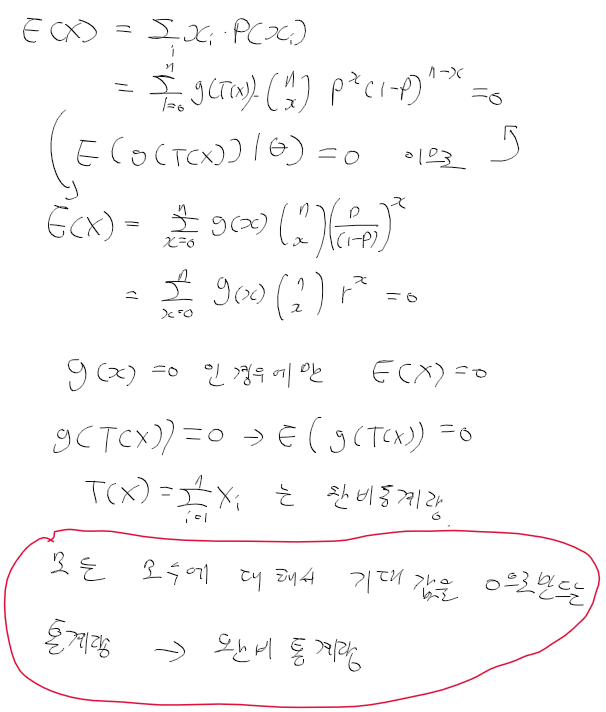
지수족 exponential family
- 확률 밀도/질량 함수가아래와 같은 형태인 경우
=> 쉽게 완비 충분 통계량을 구할 수 있다.

완비충분통계량 구하기
- X1, ..., Xn이 Poisson(lambda)를 따른는 경우. lambda의 완비충분통계량

- 확률 표본 X1, .. ,Xn이 N(0, sigma2). sigma2에 대한 완비충분통계량

Basu의 정리
- T(X)가 완비 충분 통계량이면 T(X)는 모든 보조 통계량에 독립적
좋은 추정량
- 모수 theta의 불편향 추정량 중 최소 분산인 추정량
- 불편향 추정량과 편향 추정량 등 추정량 중에서 평균 제곱 오차를 최소로 하는 추정량
균일 최소 분산 불편향 추정량 uniformly minimum variance unbiased estimator, UMVUE
- 불편향 추정량에 한정하여 찾은 추정량
- 균일최소분산불편추정량을 찾기 위해 이용되는 개념이 충분성과 완비성
=> 평균제곱오차의 최소값을 갖는 불편향 추정량

- 균일최소분산불편추정량을 구하는 방법 => 라오 블랙웰 정리
라오 블랙왤 정리

균일최소분산불편향추정량 예제
- X1, X2 가 Poisson(lambda)의 확률표본 lambda의 균일최소불편추정량
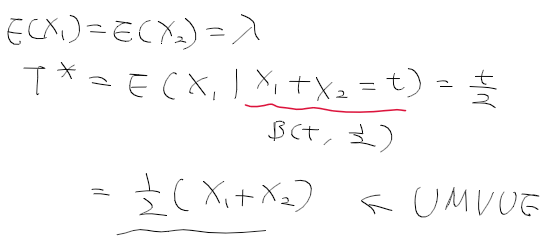
레만-쉐페의 정리
- 더 쉽게 UMVUE를 구할수 있음.

UMVUE 예제 2
- X1, .. Xn ~ Ber(p), p의 UMVUE는?

UMVUE 예제 3
- X1, .., Xn ~ N(mu,sigma2), mu,sigma2에 대한 UMVUE
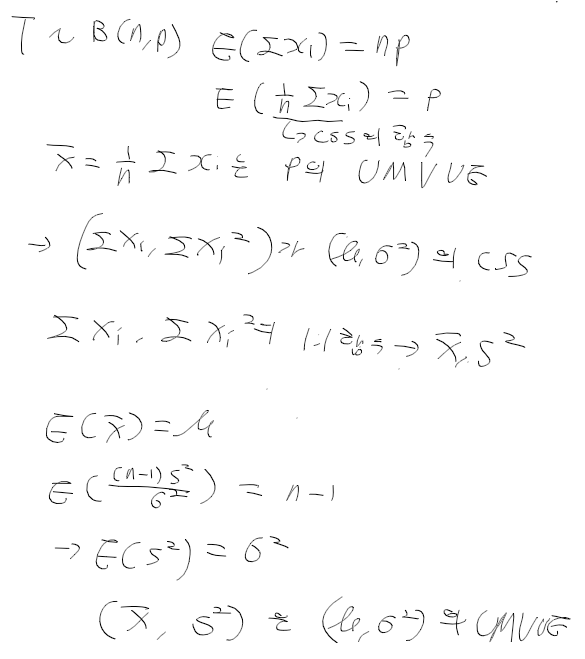
크래머-라오 하한
- 모수 theta를 추정하는 2개의 불편향 추정량이 있는 경우, 추정량의 분산이 작은게 더좋을것임
- 최소 분산을 갖는. 그러니 가장 좋은 추정량이 되는걸 알아내는 방식으로 크래머-라오 하한 제안
크래머-라오 하한 cramer rao lower bound CRLB
- 어느 불편 추정량의 분산이 크래머-라오 하한과 동일하면 이 추정량은 UMVUE

'수학 > 통계' 카테고리의 다른 글
| 통계 - 12. 통계적 추정 1 (0) | 2020.10.26 |
|---|---|
| 통계 - 11. 통계적 가설 검정 (0) | 2020.10.26 |
| 통계 - 9. 복습? (0) | 2020.10.26 |
| 통계 - 8. 점추정량 비교 (0) | 2020.10.26 |
| 통계 - 7. 점추정 (0) | 2020.10.25 |