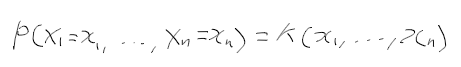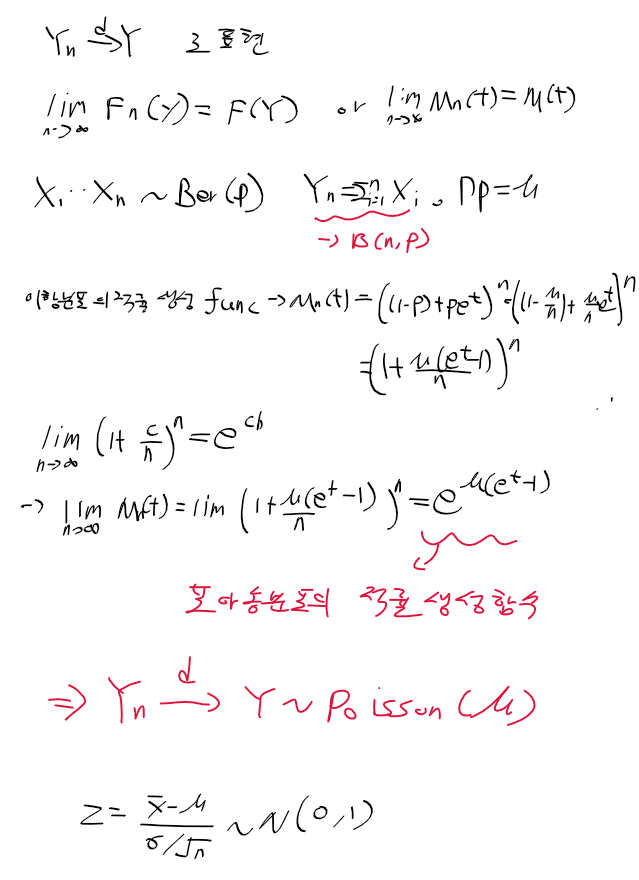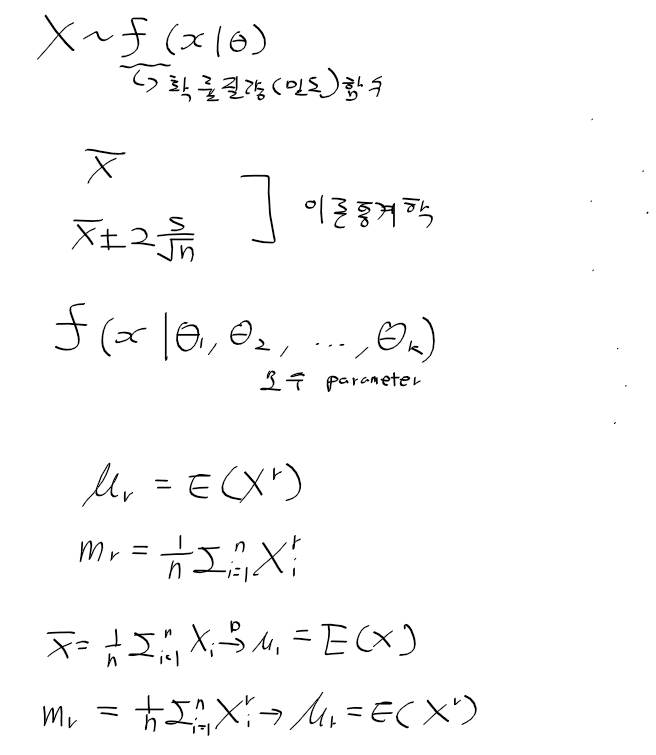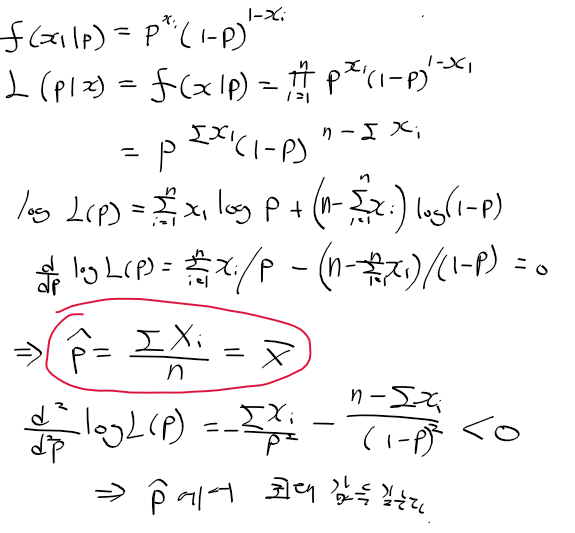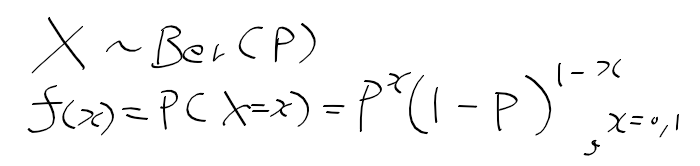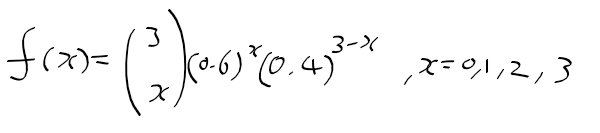집밖은 위험해

용어

- 추정 : 표본으로부터 모집단에 대한 값을 구해나가는 것

- 추정량 : 모수를 추정하기위한 표본의 함수

- 모수 : 모집단에 대한 특성을 나타내는 값

- 점 추정 : 모수에 대한 추정

- 구간 추정 : 점 추정 + 정확도 추정

- 신뢰 수준 : 모수의 참값이 속할것으로 기대되는 구간안에 모수가 포함될 가능성 확률

통계적 추론

- 우리 주위에 대한 데이터 수집, 요약

- 수집한 데이터로부터 일반성을 찾음

- 불확실한 사실에 대한 결론, 예측

기술 통계학 descriptive statistics

- 데이터의 특성들을 요약, 정리

(표본 평균, 표본 분산 등)

- 판단하기 힘듬

통계적 추론 구조

- 모집단 : 알고자 하는 관측 대상 -> 모든 관측값의 집합. 전체다 알기 힘듬

- 표본 : 모집단의 일부 -> 모집단에서 임의추출하여(모집단을 잘 대표하도록) 모집단을 추측한다.

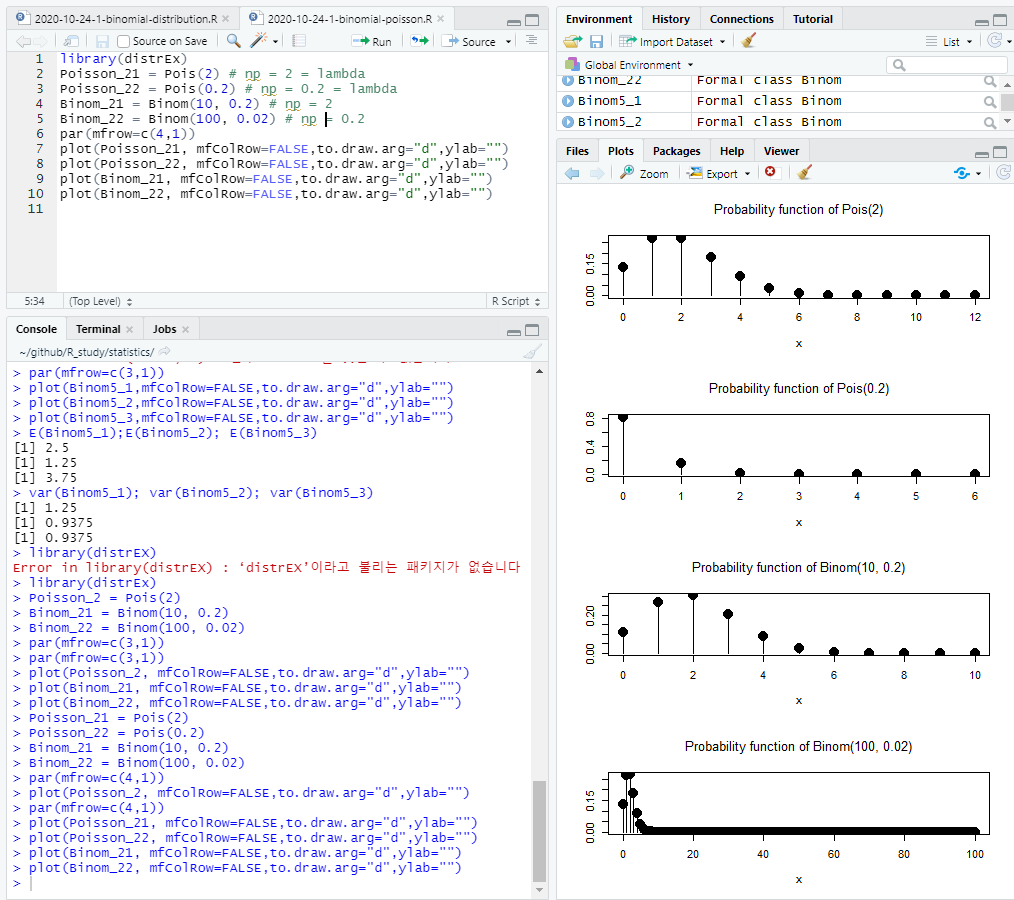
- 모집단의 변수들은 어느 확률 분포를 따름

- 확률 분포 : 몇개의 모수(평균, 분산, 첨도, 왜도, 람다 등)으로 구성된 수리적 함수

 -> 이항 분포, 정규 분포 등

모집단의 파악

- 정규 분포의 모수 : 모 평균과 모분산

- 이항분포의 모수 : 모비율

- 카이제곱 분포, t분포는 자유도에 의해 결정

통계적 추론 구조

- 통계량 : 표본의 함수 -> 모수를 추정 

 -> 표본 평균, 표본 비율, 표본 분산 등

- 추정량 : 모수를 추정하는데 사용되는 통계량

- 추정값 : 관측된 데이터를 추정량(통계량)에 대입하여 얻은 값

추정량의 분포

- 추정량은 추출한 표본들에 따라 변화하게 됨

 => 표본 분포 sampling distribution

 * 표본 분포는 추출한 샘플들에 따라 달라짐

여론조사의 분포?

- 표본들이 매번 바뀌기 때문에 표본 분포는 다름

추정과 검정

- 추정 : 표본으로부터 모집단에 대한 정보인 모수를 추측함.

- 검정 : 모집단과 관련된 주장에 대한 타당성을 표본으로 점검

 -> 표본으로 얻은 증거가 우연인지 아닌지 점검

추정

- 점추정 : 모수에 대한 하나의 추정값을 구함

- 구간 추정 : 모수에 대한 추정값과 정확도를 구함

  ex. 3% +- 1%

- 모수 theta에 대해 두 통계량 (L, U) : theta의 (1-alpha) x 100% 신뢰구간

 P(L < theta< U) = 1 - alpha

 * Lower bound 하한, Upper bound 상한

적합한 추정량

- 불편성, 일치성, 효율성

- 불편향성 : 가능한 모든 통계값의 평균이 모수가 됨

 -> 표본 평균은 모평균의 불편향 추정량

- 일치성 : 표본 크기가 커질수록 추정량의 값과 모수가 더 가까워짐

  -> 표본 평균의 분산은 표본크기가 커지면 0, 표본 평균은 모평균에 근점

- 효율성 : 추정량중 분산이 작은것을 의미

바람직한 추정량을 구하는 방법

- 최대가능도 추정법

- 적률 추정법 

- 최소제곱 추정법

최대 가능도 추정법

- 미지의 모수를 가지는 모집단의 분포에서 확률 표본을 추출하여 추정량찾음

- 표본의 몯느 정보는 결합확률밀도함수인 가능도 함수에 있으므로 최대 가능도 추정법으로 찾음

피셔의 밀크티 실험 

- 주장 : 우유에 차를 넣은 홍차와 차에 우유를 넣은 홍차의 맛을 감별할 수 있다.

- 전체 8개의 잔 중에서 차를 먼저 넣은 잔이 4잔이 있음.

- a는 홍차를 먼저 넣었다고 올바르게 판단한 잔의 수. a는 0~4 중 한가지 값.

- 해당 주장이 근거가 없다는 가정하에 여덟 잔중에 먼저 4잔을 찾아낼 확률

- 차를 넣은 네 잔을 정확히 찾을 확률을 1/70으로 매우 작음.

 => 통계적인 관점에서도 주장이 틀렷다고 말하기는 힘들다

 - 정확히 4잔을 찾기도 힘듦으로

밀크티 실험 가설

- 가설 1 : 차와 우유 둘 중 무엇을 먼저 넣었는지 알수 있다.

- 가설 2 : 차와 우유 둘 중 무엇을 먼저 넣었는지 알 수 없다.

가설 검정 개요

- 통계적 가설검정 : 확률 표본으로 모집단의 배반적인 두 가설중 무엇이 타당한지 판단

- 대립가설 H1 : 입증하려는 가설

- 귀무가설 H0 : 대립가설에 반대되는 가설

통계적 가설검정

- 실험을 통해 얻은 자료, 데이터로 어느 가설이 타당한지 판단하는 것.

- 귀무 가설이 참이라는 가정 하에 주어진 관측값보다 더 벗어난 값을 얻을 확률이 작다면

  -> 귀무 가설이 참이라는 가정은 올바르지 않다고 판단.

가설 검정 hypothesis testing 의 개요

- p-값 : 귀무 가설 하에서 주어진 관측값보다 더 극단적인 값을 얻을 확률

 -> p값이 작다는 것의 의미 : 귀무가설이 참이 아니거나 귀무가설이 참이라면 매우 희귀한 사건이 발생

- 기각역 R : 귀무가설을 기각하는 관측값의 영역

 -> 관측값이 기각역 R에 속하면 귀무가설 기각

 -> 관측값이 기각역에 속하지 않으면 귀무가설을 기각할수없음

검정 오류

- 제 1종 오류 alpha : 귀무가설이 참이라는 하에서 기각하는 확률

- 제 2종 오류 beta : 대립가설이 참이라는 가정하에서 기각하지 못하는 확률

- 검정력 :  대립가설이 참일때 귀무가설을 기각할 확률

검정력 예제

- 다음의 조건 하에 제1 종 오류, 제 2종 오류를 범할 확률, 검정력을 구해보자

- 제 1종 오류 alpha : 귀무 가설이 참이라는 가정 하여 기각하는 확률

- 제 2종 오류 beta : 대립 가설이 참이라는 가정하에 기각하지 않을 확률

- 검정력 power : 대립가설이 참일때 귀무 가설을 기각할 확률로 1 - beta

검정

- 기각역 R에 의해 결정

- R = {x | x>=c}, 제 1종 오류와 제 2종 오류

 -> c의 값에 따라 alpha가 커지고 beta가 작아지거나. 반대의 현상이 나타날 수 있음

검사 특성 곡성 operating characteristic curve

- 제 1종 오류를 작게하면 검정력이 작아짐(제 2종 오류가 커짐)

-> 제 1종 오류 alpha를 x축, 검정력 power를 y축에 둔 그래프

- 오류의 상충 : 제 1종 오류를 범활 확률을 작게하는 검정은 제 2종 오류 확률을 높임

검정의 선택

- 제 1종 오류 범확 확류이 일정 수준 이하인 검정 중 제 2 오류 범할 확률을 가장 작게하는 검정 선택

- 유의 수준 : 제1 오류를 범할 확률의 최대 한계

- 수준 alpha 검정 : 제 1종 오류를 범활 확률이 alpha이하인 검정

검정 함수

검정 함수 일반화

- 연속형에서는 괜찬으나 이산형인경우 검정 함수가 5%에 딱맞는 유의수준이 존재하지 않을수있음. 

- delta(x) = 1 : 귀무가설 기각

- delta(x) = 0 : 귀무가설 기각 x

- delta(x) = 1/2 : 귀무가설 기각확률 0.5

최강력 검정 개요

- UMVUE와 같은 개념으로 볼수 있음

- 단순 가설 simple hypothesis : 귀무가설이나 대립가설하에 X의 확률분포가 하나로 결정.

 ex. H0: theta =1

- 복합 가설 composite hypothesis : 확률분포가 하나로 결정되지 않을때 가설

 ex. H1: theta >1 , H1:theta != 1

귀무가설과 대립 가설이 모두 단순 가설인 경우

- 아래와 같이 표현 가능

 H0: theta = theta0    vs     H1: theta=theta1

최강력 검정 most powerful test

- 기각역이 R인 검정이 아래의 조건을 만족하는 경우 유의수준 alpha에서의 검정

=> 제 1종 오류를 범할 확률이 alpha 이하인 검정 중에서 제 2종 오류를 최소로 하는 검정

네이만-피어슨의 보조정리 neyman-pearson lemma

- 최강력 검정을 구하는 구체적인 방법

- 상수 k에 대해 주어지는 기각역 R이 P(X는 R의집합 | H0) = alpha일때,

 기각역 R인 검정이 유의수준 alpha에서의 최강력 검정

- f(x |theta0), f(x|theta1)은 귀무가설과 대립가설이 참인 경우 확률 밀도 함수

가능도비 검정

- 최강력검정은 귀무가설과 대립가설이 모두 단순 가설인 경우 사용 가능

- 귀무가설, 대립가설이 복합가설인 경우 사용되는 검정으로 가능도비 검정

일단 통개학 개론을 모르고 바로 수리 통계학을 하다보니 어려움을 많어서 잠깐 여기서 멈추고

개론 부터다시 시작해야될듯 싶다.

일치성

- 표본 크기가 증가할 수록 추정량의 분포가 모수로 수렴하는 성질

일치 추정량

- Tn = T(X1, ..., Xn) n개의 표본을 사용한 추정량

- {T1, ..., T_inf}는 모수 theta에 대한 점추정량 수열

- Tn을 일치 추정량이라 함.

충분성 sufficiency

- 모수에 대해 더이상 정보를 제공하는 통계량이 없는 경우.

 => 그 추정량은 충분성을 가짐

- 통계량이 표본 모수에 대한 정보를 읽지않고 모수를 추정할 수 있는 성질

- 충분통계량 : 충분성을 같는 통계량

충분 통계량

- theta에 대한 추정량 T에 대해 T가 주어졌을때 X1, X2, ..., Xn의 조건부 분포가 모수 theta에 의존하지 않을때 T

피셔-네이만 인수분해 정리

- 확률 표본 X1, ..., Xn에서 theta의 추정 통계량 T = h(X1, ..., Xn)이 충분 통계량일 필요 충분조건

=> 결합확률밀도함수가 함수 g와 h로 표현되는것.

충분 통계량 예제 1

- X1, ..., Xn이 정규분포 N(mu, 1)을 따르는 확률 표본인경우 mu에 대한 충분 통계량 구하기

완비 통계량 complete statistics

- 완비성을 갖는 통계량

- 통계량 함수의 기대값이 모든 모수에서 0인 경우 통계량 함수 값 자체가 0인 통계량

- 충분 통계량이면서 완비 통계량인경우 => 완비충분통계량(complete and sufficient statistic, CSS)

완비 통계량

- 모든 theta와 통계량 T(X)의 함수 g에 대해 아래가 성립하는경우 T(X)

- 모든 theta와 함수 g에 대해 다음이 성립 -> T(X)가 완비통계량

완비통계량 예제

- 확률 표본이 베르누이분포 Ber(P)를 따르는 경우, Sigma Xi가 p에 대한 완비통계량 증명

완비 통계량 복습

지수족 exponential family

- 확률 밀도/질량 함수가아래와 같은 형태인 경우

=> 쉽게 완비 충분 통계량을 구할 수 있다.

완비충분통계량 구하기

- X1, ..., Xn이 Poisson(lambda)를 따른는 경우. lambda의 완비충분통계량

- 확률 표본 X1, .. ,Xn이 N(0, sigma2). sigma2에 대한 완비충분통계량

Basu의 정리

- T(X)가 완비 충분 통계량이면 T(X)는 모든 보조 통계량에 독립적

좋은 추정량

- 모수 theta의 불편향 추정량 중 최소 분산인 추정량

- 불편향 추정량과 편향 추정량 등 추정량 중에서 평균 제곱 오차를 최소로 하는 추정량

균일 최소 분산 불편향 추정량 uniformly minimum variance unbiased estimator, UMVUE

- 불편향 추정량에 한정하여 찾은 추정량

- 균일최소분산불편추정량을 찾기 위해 이용되는 개념이 충분성과 완비성

=> 평균제곱오차의 최소값을 갖는 불편향 추정량

- 균일최소분산불편추정량을 구하는 방법 => 라오 블랙웰 정리

라오 블랙왤 정리

균일최소분산불편향추정량 예제

- X1, X2 가 Poisson(lambda)의 확률표본 lambda의 균일최소불편추정량

레만-쉐페의 정리

- 더 쉽게 UMVUE를 구할수 있음.

UMVUE 예제 2

- X1, .. Xn ~ Ber(p), p의 UMVUE는?

UMVUE 예제 3

- X1, .., Xn ~ N(mu,sigma2), mu,sigma2에 대한 UMVUE

크래머-라오 하한

- 모수 theta를 추정하는 2개의 불편향 추정량이 있는 경우, 추정량의 분산이 작은게 더좋을것임

- 최소 분산을 갖는. 그러니 가장 좋은 추정량이 되는걸 알아내는 방식으로 크래머-라오 하한 제안

크래머-라오 하한 cramer rao lower bound CRLB

- 어느 불편 추정량의 분산이 크래머-라오 하한과 동일하면 이 추정량은 UMVUE

확률 관련 기초 용어

- 확률 probability : 확률 변수가 특정한 값/구간에 속할 가능성으로 0 ~ 1의 값으로 표현

- 확률 실함 random experiment : 결과를 알수 있는 실험

- 시행 trial : 확률 실험을 수행하는 행위

- 원소 element : 시행의 결과

- 표본 공간 sample space : 모든 원소들의 집합

- 사건 event : 표본 공간의 부분집합으로 관심 대상(원소)로 구성

확률의 정의

- 빈도주의 정의  : 관심 사건 횟수/ 전체 실험의 횟수

  => P(A) = lim n(A)/n

- 주관주의 확률 : 믿음의 정도

확률 변수 random variable

- 확률 실험의 모든 가능한 결과에 일정한 규칙에 따라 특정 값을 부여한 것

- 표본 공간을 실수로 변환하는 함수

- 정의역이 표본공간, 치역이 실수인 함수

확률변수 예제

확률 변수 X ~ B(3, 1/2)

동전 던지기

앞면의 횟수    0     1     2      3

확률           1/8   3/8   3/8   1/8

복습

표본 분산의 확률 분포

- 대표적으로 카이제곱 분포와 t분포가 있음.

카이제곱분포

- 모분산 추정, 적합도 검정, 교차표 검정에 사용

- 감마 분포의 특수한 경우 r = n/2, lambda = 1/2인 경우 확률변수 X는 

 => X ~ chi2(n)으로 표현

카이제곱 분포의 특성

표본분산 S2의 확률분포

t분포의 필요성

- 보통 모집단이 정규분포를 따르고, 확률변수들이 독립이면 아래와 같으나

- 보통 확률 표본을 추출한 경우 모집단의 분산을 알수 없음

 => 표본분산 S2를 구하고 sigma2대신 사용. 

- 의문점 : S로 대채한 다음 통계량의 분포는 어떻게 될까?

t분포

- 위 통계량의 분포는 정규분포가 아니라 t분포를 따름

- t 통계량의 pdf를 구하려면 정규분포와 카이제곱분포를 사용해야함. 

t분포의 확률밀도함수

- 변수 변환법으로 구하면

적률 추정량

최대 가능도 추정량

어떤 추정량이 좋은 추정량인가?

=> 불편 추정량, 추정량 효율성, 일치추정량, 평균제곱오차를 보자

추정량 estimator

- 모수를 추정하는데 사용되는 통계량 (표본의 함수, 표본평균/표본분산)

추정값 estimate

- 데이터에 근거한 추정량 값

좋은 추정량

- 추정량의 값이 모수와 항상 일치

- 추정량 선택 기준 : 불편성, 효율성, 일치성

추정량의 성질

- 불편성 : 평균하면 모수가 되는가

 => 불편 추정량 unbiased  estimator : 불편성을 가진 통계량

- 효율성 : 얼마나 밀집되어있는가

- 일치성 : 수렴한느가

불편향추정량 unbiased estimator

- 통계량 T가 다음을 만족하면 T는 불편 추정량

 => 불편향 추정량 : E(T) = theta

 => 불편향 추정량의 기대값은 모수가 됨.

편향 추정량 biased estimator

- 불편향 추정량이 되지 못하는 추정량

 => 편의 : bias(T) = E(T) - theta

불편향추정량 예제

- X1, ..., Xn ~ Poisson(lambda)를 따르는 확률표본인 경우

- T1 = bar{X}이 불편추정량임을 증명

=> E(T1) = E(bar{X}) = lambda로 모수임을 증명함

편향 추정량 예제

- 다음 추정량의 편향을 구하라

효율성 efficiency

- 분산의 역수

- 불편 추정량 hat{theta}의 효율성

효율성 예제

- X1, ..., Xn ~ N(mu, sigma^2)을 따르는 확률 표본

- S2과 hat sigma2의 효율성을 구하라

- 

상대 효율성 relative efficienty

- 하나의 모수를 추정하는 2개의 불편 추정량이 있다면, 그 성능은 효율성으로 비교

- 모수 theta에 대해 불편추정량 T1, T2가 있을떄 T1에 대한 T2의 상대효율성

평균제곱오차의 필요성

- 불편 추정량과 편의 추정량 비교를 하기 위해 아까 본 예제를 다시보면

- 편향성과 효율성을 동시에 고려해야하며 기준 필요

=> MSE

평균제곱오차 Mean Sqaure Error, MSE

- 추정량 T와 모수 theta간 거리 제곱의 평균 측정값

- 통계량 T가 추정 통계량인 경우 T에 대한 평균제곱 오차는 다음과 같다.

평균 제곱 오차의 정리

- 통계량 T에 대한 평균 제곱 오차를 편향과 분산으로 나누면 다음과 같다.

평균 제곱오차 예제

- X1, .., Xn이 N(mu, sigma2)를 따르는 확률 표본인경우 추정량의 효율성과 평균제곱오차를 구해보자

- S2의 효율성과 평균 제곱오차

- sigma2 추정량의 효율성과 평균제곱오차를 구해보자

점추정 열심히 정리했는데 잘못 저장해서 날려먹엇다 ..

그냥 필기한거 복붙

적률 추정법

정규분포 적률 추정량 구하기

가능도 함수와 최대가능도함수로 최대 가능도추정량 구하기

최대가능도법으로 모수 p 추정하기

베르누이분포 최대가능도 구하기

정규분포 최대가능도 구하기

단순 선형 회귀 모델 simple linear regression model

- 회귀계수 beta0는 절편 intercept, beta1은 기울기 slope, 오차 epsilion ~ N(0, sigma^2)

단순 선형 회귀 모델 예제 - 회귀계수 beta0, beta1의 최대가능도추정량을 구하자

R 실습

1. 베르누이 분포 최대 가능도 함수로 확률 구하기

2. 정규분포 최대 가능도 함수

표본으로 추정한 모수(평균 키와 분산)

  1. 최대 가능도 함수로 모수 추정

  2. 가능도 함수로 데이터 만들고 plot

3. 단순 선형회귀 모델 beta0, beta1, sigma^2 최대 가능도 추정량 구하기

통계량들의 차 비에 대한 분포

극한 분포 - n이 커질떄 어떻게 수렴하는지

표본 평균의 차에 대한 분포

- 다음과 같은 표본이 주어질떄

- 표본 평균은

- 표본 평균의 차를 적률 생성 함수로 구할 수 있음

- sigma1과 sigma2가 동일하다고 가정하면 다음과 같이 표준화하면 표준 정규분포를 따르게됨

공통 분산

- 각각의 분산들을 추정할때 다음과 같이 계산

- X와 Y를 합한 공통 분산을 구하고, 이에 대한 카이제곱 분포는 m+n -2 자유도를 따름

표본 평균의 차에 대한 분포

- 두 집단 모분산을 모르지만 같다고 가정시, m+n - 2의 자유도를 같는 T분포를 따른다

표본 분산 비교

- 표본 분산의 경우 차 보다는 나누어서 주로 비교

F 분포

- 표본 분산비 : 카이제곱 통계령의 비 -> F분포로 표현됨. 분산분석법에 이용됨

- Fisher를 기르기위해 F분포라 명명

표본 분산의 비교

극한분포

- 표본수가 무한대가 될떄 어떻게 되는지

확률적 수렴

- 모집단이 N(mu, sigma^2)을 따르면, 표본 평균은 N(mu, sigma^2/n)을 따름

- n이 무한이 되면 표본 평균 bar{X}는 mu에 근접(약대수의법칙)

마르코브 부등식

- 약대수 법칙을 증명하기 위해 필요

- 확률변수 X가 주어지고 u(X)가 양의 함수일때 epsilon > 0에 대해 다음이 성립

약대수의 법칙

- X1, ... Xn 이 주어질떄 E(Xi) = mu, 분산 Var(Xi)= sigma^2인 모집단에서 확률 표본일때

- 표본평균 bar{Xn}은 상수 mu에 확률적으로 수렴

예제

- 표본 분산이 확률적으로 모분산에 수렴함을 증명하라

분포로 수렴

- 확률 변수가 하나의 값이 아닌 어떠한 분포로 수렴할수 있음

- 분포의 수렴을 알려면 CDF나 적률생성함수 사용

- 여기서 각 Yi의 누적 분포 함수 Fn(y)에서 n이 무한이 커진 F(y)를 극한 누적 분포 함수 limiting distribution이라 부름.

분포 정리 

- 베르누이 분포 : 베르누이 시행에 대한 분포

- 이항 분포 : 베르누이 시행을 n번 한 경우에 대한 분포

- 포아송 분포 : n이 충분히 크고, p가 작고, np가 lambda를 따르는 분포로 사건 발생 횟수에 간한 분포

- 지수분포 : 포아송 분포의 특수한 경우로 사건이 처음 발생할때까지 수명에 관한 분포

- 감마 분포 : gamma 번째 발생할 확률에 대한 분포

- t 분포 : 모분산을 모를때, 표본 분산의 분산을 구하기 위한 분포

- 카이제곱 분포 :  감마분포의 특수한 경우, t분포와 마찬가지로 통계량 추정을 위해 사용

분포 수렴 예제 - n이 무한이 커질때 이항분포가 포아송 분포를 따름을 증명

표본 평균의 분포

1. Xi가 정규분포를 따르는 경우

2. 정규 분포를 아니더라도. n이 무한이 커지면 정규분포로 수렴하게 된다.

R 실습

1. 정규 분포와 정규분포의 합 분포

2. 이항 분포 합의 분포 , 포아송 분포의 합의 분포, 정규분포 합의 분포, 정규분포 평균의 분포

그동안 계속 모집단에 대한 분포들을 연습했는데

모집단에서 추출한것이 표본이고

표본 수가 많으면 정규분포의 형태를 따르는 다나, 표본 평균의 평균/분산 까지는 이해가 되지만

표분 분산의 평균, 분산부터는 햇갈리기 시작한다 그래서 

다시 표본 분포에 대해서 살펴보고자 한다

앞서 살펴보니 이 파트에서는

확률 표본을 구성하는 확률 변수. 합의 분포와 변수 변환법으로 확률 변수함수의 분포를 본다고 한다.

내가아는 용어

* 확률 변수 : 표본 공간을 수로 만들어주는 함수  였엇지..

* 통계량 : 평균, 분산 등.

그 다음에는 확률 표본의 통계량인 표본 평균, 표본 분산과 관련된 분포 등에 대해서 다시 보자.

다시 용어정리

- 확률 표본 : 모집단에서 독립적으로 추출한 표본

- 통계량 : 모수 추정에 적합한 확률 표본들의 함수

   ex. 표본 평균, 표본 분산

- 표본 분포 : 통계량의 확률 분포

 ex. 표본 평균의 평균과 분산, 표본 분산의 평균과 분산

- 변수 변환법 : 확률 변수 함수에 대한 확률 밀도 함수를 구하는 방법

- 카이제곱분포 : 포본 분포에 대한 분포

이산형 변수 변환

- 통계량은 확률 변수의 함수

- 통계량 분포를 구하기 위해선 확률 변수 함수에 대한 분포를 구해야함

이산형 변수변환 예시 - 새로운 확률 변수의 확률 분포 구하기

연속형 확률 변수

- 이산과 달리 점확률이 존재하지 않으므로 누적 확률 분포를 사용하여야 함.

- 새 변수 Y에 대한 확률 밀도를 구해야하므로 미분하면 

연속 확률 변수 변환 예제

합과 평균의 확률분포

- 표본으로 구한 통계량들을 보면 확률 변수의 합 형태가 됨

=> 확률 변수 합의 확률 분포는 변수 변환법을 사용할수도 있지만 적률 생성 함수를 사용할수도 있음.

적률 생성 함수 성질

적률 생성함수 예제 1

- X_i ~ B(n_i, p)의 경우 X1 + X2의 확률 분포를 구해보자

적률 생성함수 예제 2

- Xi ~ Gamma(gamma_i, lambda), X1 + X2 + X3 + X4의 분포를 구해보자

카이제곱 분포

- 통계적 추론을 위해선 표본 평균과 표본 분산의 확률분포를 알기 위해서 필요한 분포로 카이 제곱, t분포가 있음

- 모분산 추정, 적합도 검정, 교차표 검정에 이용

- 감마 분포의 특수한 경우로 Gamma(r, lambda)에서 r = n/2, lambda = 1/2임

 => 확률 변수 X는 자유도 n인 카이제곱 분포를 따르게 됨.

*  원랜 비대칭적이나 자유도가 커질수록 대칭적으로 됨.

카이제곱 분포의 기댓값, 분산, 적률 생성함수

카이제곱 분포의 특성

- 정규 분포를 따르는 확률변수 Xi를 표준화 하고 제곱하면 자유도가 1인 카이제곱 분포를 따르게 된다.

- 확률 변수가 (n-1) 표본분산/분산인 경우, 자유도가 n-1인 카이제곱 분포를 따른다.

연속 확률 분포 continuous probability distribution

- 균등 분포, 정규 분포

- 지수 분포, 감마분포, 베타 분포, 카우치 분포 등

균등 분포 uniform distribution

- 확률변수 X = b - a

- a분에서 b분까지 기다리는 시간

균등분포의 확률밀도함수

균등 분포의 기댓값과 분산

지수분포 exponential distribution

- 사건이 첫 번쨰로 발생할때 소요되는 대기시간 T의 분포

       T ~ Exp(lambda)

지수분포와 포아송 분포

- 포아송 분포가 n이 충분히 클때 p이 0에 가까운 사건이 발생 횟수에 대한 확률 분포

- 버스 정류장에 한 시간에 5대씩 온다고 하면

- t 시간당 버스 도착 대수는 Poisson(5t)를 따른다고 할수 있다.

=> 쭉 전개해 나가면 지수 분포의 확률 밀도 함수를 구할 수 있다.

지수분포의 기대값, 분산, 적률생성함수

지수분포의 망각성

- a시간 동안 사건 발생 하지 않았다고 할떄, b를 더 기다리는 확률.

- 처음 a시간 만큼의 대기시간은 상관없음

지수분포 예제

- 노트북 수명 X가 평균 10년으로 Exp(1/10)을 따른다면, 5년 동안 사용한 노트북을 5년 더 사용할 확률

감마분포 gamma distribution

- r번쨰 사건이 발생할떄까지 대기시간 T의 분포

- T ~ Gamma(r, lambda)

* 감마분포도 지수분포와 마찬가지로 포아송 분포와 관련

감마 분포 예제

- 비행기 엔진이 두번째 결함이 일어나는 기간을 Gamma(2, 0.1)을 따를떄, 결함이 5년 뒤 나타날 확률

감마분포 기대값, 분산, 적률 생성함수

포아송/지수/감마, 카이 제곱 분포

- 포아송 분포 : n이 충분히 크고, p=0에가깝고, np=lambda일떄, 발생 횟수에 관한 분포 Poisson(lambda)

- 지수 분포 :  첫번째 사건이 발생할때까지 대기시간 T의 분포 Exp(lambda) = Gamma(1, lambda)

- 감마 분포 : r번째 사건이 발생할때까지 대기 시간 T의 분포 Gamma(r, lambda)

- 카이제곱분포 : Gamma(r, 1/2)

정규 분포 normal distribution

- 종모양의 대표적인 확률분포

- X ~ N(mu, sigma^2)

- 평균(기대값) mu : 위치 모수 location parameter

- 분산 : 척도 모수 scale parameter

정규분포의 적률 생성 함수

R 실습

1. 이항 분포

확률 변수

- 표본 공간을 수로 바꾸는 함수

확률 분포

- 이산형 확률 변수 : 베르누이 분포, 이항분포, 포아송 분포, 기하/초기하분포

- 연속형 확률 변수 : 균등분포, 지수분포, 감마분포, 정규분포 등

베르누이 분포

- 베르누이 시행 : 시행 결과가 두가지 중 하나 뿐인 시행

- 비르누이 시행의 확률 변수 X에 대한 분포

 ex. 불량품 여부, 찬성 여부

베르누이 분포 예시

- 게임 승리률이 60%라 가정할때, 승리 시 확률변수가 1 아니면 0인 경우 확률질량함수

베르누이 분포의 기대값, 분산, 적률생성함수

이항 분포 Binomial distribution

- n번 베르누이 시행을 독립 적으로 반복했을때 성공 횟수를 확률 변수 X로 할때의 확률분포

 ex. 동전을 n번 독립적으로 던진경우 앞면 총수

이항 분포의 예시 1

- 게임 승리율이 60%, 게임 3회시 승리 횟수(X)에 대한 확률 질량 함수는

이항 분포의 예시 2

- 위 예시에서 3번다 승리할 확률

이항 분포의 기대값, 분산, 적률생성함수

포아송 분포 Poisson distributioni

- 특정 기간/영역에서 사건이 일어날때 사건의 수를 확률 변수로 하는 분포

1. 이항분포에서 n이 충분히 크고

2. 성공률이 p가 0에 가까우며

3. 평균이 np = lamdba인 분포

포아송 분포의 기대값, 분산, 적률 생성 함수