점추정에서는 모수의 한 값만을 추정하였다면
모수만 아니라 모수를 포함하는 구간 또한 추정이 가능함
-> 모평균, 모분산 구간추정방법
점 추정 point estimation
- 모집단이 정규분포를 따를때 모평균 mu에 대한 추정시
- mu의 최대가능도 추정량은 표본 평균과 동일하다

=> 주어진 자료로 모수 추정값 획득.
예제
- 다음 5개 데이터가 주어질떄 모평균 추정량을 구하자
- 10, 15, 5, 10, 15
-> 표본이 작을때 표본에 따라 모평균 추정량이 크게 바뀜

구간 추정 interval estimation
- 모수를 포함할 것으로 기대되는 구간을 제시하여 모수 추정

신뢰 구간 confidence interval
- 95% 신뢰구간 : theata에 대한 95% 신뢰구간을 구하는 과정을 100번 반복시, 100개의 신뢰 구간 중 95개가 모수포함

신뢰구간 예시
- sigma = 2, 최대가능도 추정량 theta = 15인 경우, 모수 theta에 대한 95% 신뢰구간은 아래와 같다.

신뢰 수준
- 신뢰구간을 구하는 과정을 반복 시, 모수를 포함하는 신뢰 구간의 비율의 극한
정규 모집단에서 모평균에 대한 구간 추정
- X1, ..., Xn ~ N(mu, sigma2), sigma2을 알때
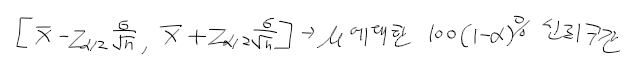
정규 모집단 모평균에서 구간 추정 2
- X1, ..., Xn ~ N(mu, sigma2), sigma2을 모를때(t분포)

정규분포를 따른는 모집단에서 모평균 mu에 대한 신뢰구간 추정하기
- X1, ..., X16 ~ N(mu, sigma2) 이고
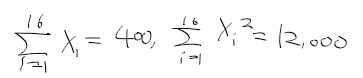
- sigma가 10, 모평균에 대한 95%신뢰구간

- 모표준편차가 알려져있지 않을때, 모평균에 대한 95% 신뢰구간 구하기

일반 모집단 모평균에 대한 구간 추정하기
- X1, ... Xn이 주어질때 모평균은 mu, 분산은 sigma2, sigma2는 미지
- 아래는 근사적으로 표준정규분포를 따름
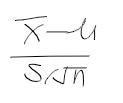
- mu에 대한 100(1-alpha)% 신뢰구간
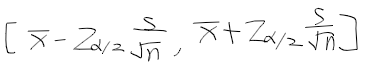
일반 모집단 모평균에 대한 구간 추정 예제
- X1, .., X100 의 확률 표본이 주어지고 아래의 경우

- 모평균에 대한 95%신뢰구간

모분산에 대한 구간 추정
- 모집단이 N(mu, sigma2)를 따르는 경우, sigma2는 표본분산 S2로 구하기 가능.
- 확률 표본 X1, ..., Xn의 모집단이 위와같은경우 표본 분산의 확률 분포는 다음과 같음.
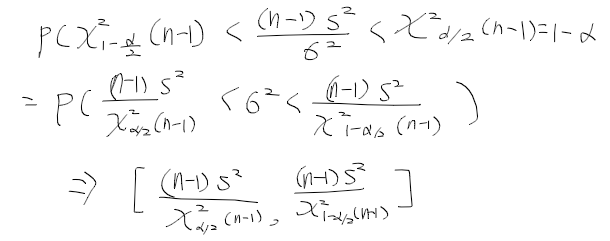
모분산 구간추정 예제
- 모집단이 정규분포를 따르고, 표본크기가 10, 표본분포 S2 = 9.8인경우 sigma2에 대한 95%신뢰구간
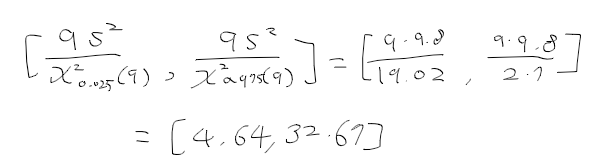
구간추정 interval estimation과 가설검정 hypothesis tset 사이 관계
- 유의수준 alpha에서 가설 H0 : mu = mu0 기각 못하는 범위

=> 모평균 100(1-alpha)% 신뢰구간과 일치
- mu 신뢰구간 = {mu | H0 : mu = mu0 기각하지 못함}
100(1-alpha) % 신뢰구간
- 유의수준 alpha에서 H0 : theta = theta0에 대한 채택역 A(theta0)
* 채택역 acceptance region : 귀무 가설을 기각하지 못하는 관측값의 영역

- 유의수준 alpha에서 채택역 A(theta0)일때 다음 식 성립

- theta에 대한 100(1-alpha)% 신뢰구간 이며, 주어진 X에 대해 모수의 집합 C(X)는 다음과 같다.

'수학 > 통계' 카테고리의 다른 글
| 통계 - 16. 실험계획법과 검정 (0) | 2020.10.27 |
|---|---|
| 통계 - 15. 표본 분포와 가설검정 (0) | 2020.10.27 |
| 통계 - 13. 통계적 가설 검정 2 (0) | 2020.10.26 |
| 통계 - 12. 통계적 추정 1 (0) | 2020.10.26 |
| 통계 - 11. 통계적 가설 검정 (0) | 2020.10.26 |