구형 공분산 가우시안 Sphere Covariance Gaussian
- 공분산 행렬이 아래와같이 분산 * 단위행렬의 경우
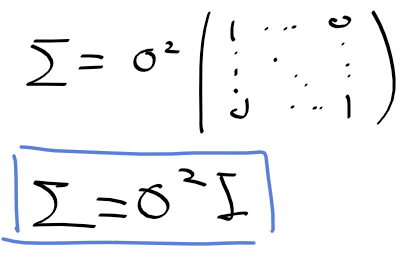
- 확률 밀도 함수로 구하기 위해 D + 1개의 파라미터가 필요하며, mu와 스칼라 분산은 아래와 같이 추정
* 표본 평균 hat{mu}와 각 차원별 분산값 hat{sigma^2} => 표본 평균 1개 + 분산값 D개.
=> 구형 공분산 가우시안을 모델링하기 위해선 D + 1개의 파라미터가 있으면 수학적 모델링 가능.
+ 데이터가 적고, 계산속도도 빠르고 유용함


대각 공분산 가우시안 Diagonal Covariance Gaussain
- 공분산 행렬 Sigma가 대각 행렬인 경우, 확률 밀도 함수 모델을 하기위해선 2D차원의 파라미터들이 필요

- 각 차원별 표본 분산 hat{sigma_i}와 표본 평균 hat{mu_i} => 표본 분산(D)개 + 표본 평균(D)개 = 2D
-> 데이터가 축에 평형하게 타원 분포.
=> 특징들간의 상관 관계는 무시함
=> but. 학습 데이터와 모델링 성능 사이 절충. 혼합 모델 사용시 유용


완전 공분산 가우시안 형태 full covariacne gaussian
- 공분산 행렬 Sigma가 아래와 같이 완전 공분산 행렬인 경우

- 완전한 확률 밀도 함수 모델링 하기 위해서 D + D(D+1)/2개의 파라미터 필요
- 학습 데이터로 mu와 Sigma 추정가능

- 완전 공분산 가우시안 형태를 사용하지 않는 이유
=> 특이 행렬 singular matrix이 되어 역행렬을 계산할수 없을 수 있음. sphere 타입 만으로도 충분한 성능을 보임

복습) 특이행렬과 비특이 행렬, 랭크
- 행렬 A가 주어질떄
- 특이 행렬 : A의 랭크가 행/열 길이보다 작은 경우
- 비특이 행렬 non singular matrix : 행렬 A의 랭크가 행/열 길이와 같은 경우
* rank(A) : 행렬 A의 행(열)벡터가 선형 독립인 경우의 갯수. 행이 m개라고 m개다 선형독립이 아닐수 있음.

'수학 > 공업수학, 확률' 카테고리의 다른 글
| 통계 - 9. 우도비 검증 개요 (0) | 2020.08.03 |
|---|---|
| 통계 - 8. 가우시안 분포 매트랩 실습 (0) | 2020.08.03 |
| 통계 - 6. 가우시안 분포들 (0) | 2020.08.03 |
| 통계 - 5. 벡터 확률변수/다변수 확률변수 (0) | 2020.08.03 |
| 통계 - 4. 기본 확률 변수 (0) | 2020.08.03 |