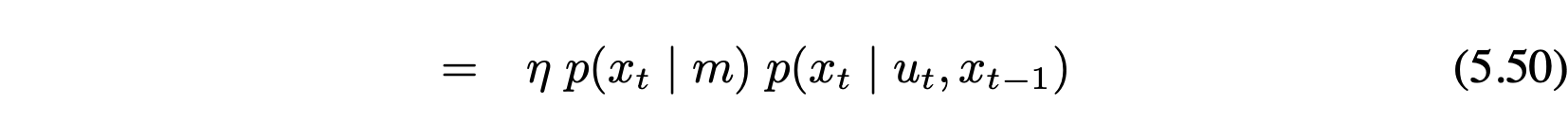집밖은 위험해

6.4.2 우도 필드 추가사항 extensions

 전에 다루었던 빔 기반 모델에비해 우도 필드 모델의 이점은 부드러움이라 할 수 있습니다. 유클리디안 거리의 부드러움으로 로봇의 자세 $x_t$에서 약간의 변화는 결과 분포 p($z_t^k$ | $x_t$, m)에서 약간의 영향만을 가지게 됩니다. 다른 주요 이점은 3차원 대신 2차원에서 전계산이 수행되어 전계산된 정보의 조밀함이 더 커지게 됩니다.

 하지만 이 모델또한 3가지 주요 단점을 가지고 있는데, 첫째는 짧은 거리로 읽힐수 있는 사람이나 다른 동역학을 설계할수 없는 점이고, 2번째는 벽너머도 볼수있는것처럼 센서를 사용하는데, 이는 광선 투사 동작이 최근접 이웃 nearest neighbor 함수로 대체되기 때문입니다. 이 최근접 이웃 함수는 점까지의 경로가 지도상의 장애물로 가로막히는지 아닌지 판단할수 있는 능력을 가지지 못하고 있습니다. 셋 째 이유는 여기서는 지도의 불확실성을 고려하지 않았습니다. 확실히 얘기하면 확인하지 않은 공간들을 다룰수 없으며, 이 공간들은 명시되지 않거나 매우 큰 불확실성을 가지고 있습니다.

 우도 필드 거리계 모델 기본 알고리즘들은 이 제한들의 영향을 줄이도록 개선시킬수가 있는데, 예를들어 기존의 2가지 값을 사용하던 지도를 3가지 카테고리의 값(점유, 텅빈, 알수없음)으로 사용하는 방법이 있습니다. 센서 측정 $z_t^k$가 알수없음 카테고리에 해당될때, 그 확률 p($z_t^k$ | $x_t$, m)은 상수 값인 $\frac{1} {z_{max}}$라 가정합니다. 확인되지 않은 공간에서의 확률적 모델 결과는 센서 측정값이 동일하다고 봐서 p($z_t^k$ | $x_t$, m)는 밀도 $\frac{1} {z_{max}}$에 대한 균일 분포로 설계 됩니다.

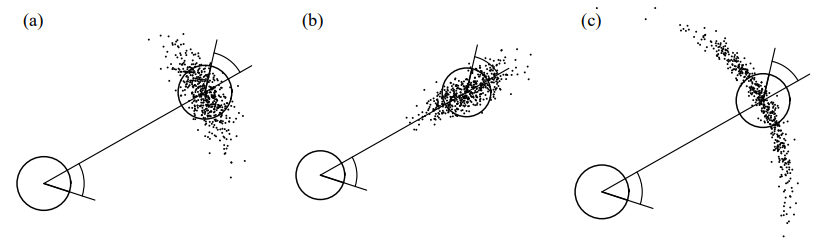
그림 6.9 (a) 샌 조스 테크 박물관 san jose tech museum의 점유 격자 지도, (b) 전처리된 우도 필드

 그림 6.9는 지도와 그에 대한 우도 필드를 보여주고 있습니다. 여기서 x-y 위치의 회색 정도는 센서가 읽은 우도치를 알려주며, 여기서 최근접 장애물까지의 거리가 지도 안에 있는것으로 판단되어 탐사된 공간으로 본다는것을 알 수 있습니다. 바깥의 우도 p($z_t^k$ | $x_t$, m)는 상수 값이 됩니다. 계산을 효율적으로 하기 위해서 2차원 그리드에서 최근접 이웃 전계산이 중요한데, 볼수 있는 공간 전반에 대한 우도 필드는 지역 지도를 정의하는 최근 스캔으로 구할 수 있습니다. 직관적으로 확장하자면 스캔 데이터와 맵을 체계적으로 매칭시키고, 맵 안에 스캔된 우도 필드를 계산을 수행함과 더불어 체계적인 확장이 스캔된 우도 필드에 상대적인 물체에 대한 우도를 계산합니다. 이러한 체계적인 루틴은 이후 맵핑에서 중요하게 다루어 질것인데 이 스캔들을 정리하여 맵을 만들게 됩니다. 간결하게 일단 표 6.3에 대한 알고리즘을 구하는 과정은 생략하겠습니다. 하지만 우도 필드 기술 구현이 이 확장된 체계적인 알고리즘이 사용됩니다.

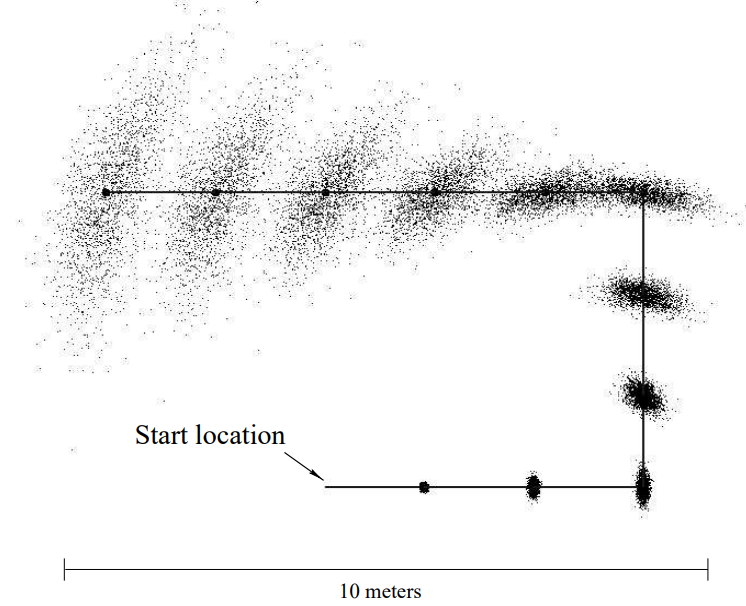
그림 6.10 (a) 버드 아이 뷰로 본 센서 스캔. 로봇은 그림 바닥에 위치하여 180도 전방에 대한 스캔 데이터를 생성

(b) 센서 데이터로 생성한 우도 함수. 검은 지역일수록 물체가 거기에 존재할 우도가 작음. 점유된 지역은 하얗게됨.

6.5 상관관계 기반 센서 모델 correlation-based sensor model

 측정치와 지도사이에 상관관계를 측정하는 다양한 거리 센서 모델들이 존재하는데, 여기서 대표적인 기술로 지도 매칭 map matching이 있습니다. 지도 매칭은 이후 챕터에서 다룰것이지만 스캔 데이터를 점유 격자 지도에 변환을 수행합니다. 일반적으로 맵 매칭은 연속적인 약간의 스캔 데이터를 지역 지도 local map $m_{local}$로 변환시키는 것으로 그림 6.11이 점유 격자 형태의 지역 지도를 보여주고 있습니다. 관측 모델은 지역 지도 $m_{local}$을 전역 지도 m에 비교하는데 p($m_{local}$ | $x_t$, m)가 클수록 m과 $m_{local}$이 더 비슷해집니다.

 지역 지도는 로봇 위치에 상대적인 표현으로 비교하기 위해선 지역지도의 셀들을 전역 지도 좌표계상으로 변환을 해야합니다. 이 변환은 우도 측정 모델이 사용된 센서 측정의 좌표 변환 (6.33)과 비슷하게 수행되는데, 로봇이 위치 $x_t$에 존재하면 $m_{x, y, local}$($x_{t}$)로 나타내며 지역 지도의 그리드는 전역 좌표계의 (x y$)^T$에 대응하게 됩니다. 둘다 같은 기준 좌표계에 존재한다면, 아래와 같이 정의되는 지도의 상관 함수로 비교할수 있는데

 여기서 모든 셀에 대한 합은 지도 둘다 다음과 같이 정의할 수 있고, $\bar{m}$은 지도의 평균값이 됩니다.

 N은 지역 지도와 전역 지도 사이 겹친 요소의 수를 나타냅니다. .상관관계 $\rho_{m, m_{local}, x_t}$의 스케일은 +-1로, 맵 매칭은 로봇의 자세 $x_t$와 전역 지도 m이 주어질 때 지역 지도의 확률로 정리할 수 있습니다.

 맵 매칭은 수많은 성질들을 가지고 있는데, 자세 파라미터 $x_t$에서 부드러운 확률을 구할수 있지는 않지만 우도 필드 모델처럼 계산하기 쉽습니다. 이 우도 필드를 근사화하는 방법은 지도 m을 가우시안 커널과 컨볼루션을 하고 이 부드러워진 지도를 맵매칭을 수행하면 됩니다.

 가우시안 필드에서 맵매칭의 가장 큰 이점은 두 지도 사이의 점수에서 자유 공간을 도려하는 점인데, 우도 필드 기술은 점유된 공간이라고 판단하는 스캔의 끝점만을 다룹니다. 하지만 많은 지도 맵핑 기술들은 센서 너머서도 지역 지도를 만들게 됩니다. 예를 들면 이 기술들은 실제 센서 측정 거리의 0.5까지만 측정하도록 설정하면 로봇 주위로 원형 지도를 만들게 됩니다. 이런 경우처럼 센서가 벽 너머서도 볼수있는것 처럼 실제 측정 거리를 벗어난 공간을 합칠때 위험할 수 있습니다. 이런 사이드 이펙트는 수많은 맵 매칭 기술들에서 볼수 있습니다. 이 단점은 맵 매칭이 물리적으로 합리적이라고 할수는 없지만, 상관관계가 지도 사이의 2차적인 거리를 정규화 되어집니다.

6.4 거리계에 대한 우도 필드 likelihood fileds for range finder

6.4.1 기본 알고리즘

 거리계의 기하학과 물리계에 크게 연관된 빔 기반 센서 모델은 2가지 결점을 가지고 있씁니다.

1. 평활도 부족 lack of smoothness

- 작은 장애물들이 많이 흩어진 환경에서, 분포 p($z_{t}^{k}$ | $x_t$, m)는 $x_t$에서 보다 매우 덜 평활할 수도 있습니다. 예를들어 컨퍼런스룸 처럼 의자와 테이블이 많은 공간을 생각해보면, 1장에서 보았던 로봇은 장애믈의 다리들을 감지하겠지만 로봇의 자세 $x_t$가 약간 변화면 센서 빔의 정확한 거리에 큰 영향을 줄겁니다. 그결과 관측 모델 p($z_{t}^{k}$ | $x_t$, m)는 크게불연속적으로 됩니다.이러한 평활도 부족은 2개의 문제를 발생시큰ㄴ데,첫번째는 신뢰도 근사값이 올바른 상태를 놓칠수 있는 위험이 있고, 급격히 다른 사후확률 우도를 가지게 될것입니다. 이 자세는 근사시 제약을 시키나 사후확률에 있어 에러를 증가시켜버립니다. 두번째는 정확한 상태를 찾기 위해 언덕 오르기 방법 hil climbing methods들은 비평활 모델에서 많은 수가 지역 최대가 되기 때문에, 지역적 최소치가 되기 슆습니다.

2. 계산 복잡도 Computational complexity

- 각 개별 센서 측정값 $z_{t}^{k}$에 대한 p($z_{t}^{k}$ | $x_t$, m)의 계산에는 비용이 큰 광선 투사도 포함됩니다. 위에서 봤지만 이 문제는 자세에서 이산 그리드로 거리를 전처리하여 완화할수 있으며, 더 빠르게 동작할수 있게 됩니다. 하지만 매우 큰 3차원 공간인 경우 결과는 매우 커지므로 거리 사전계산도 큰  계산비용과 추가적인 메모리를 필요로 하게 됩니다.

 그래서 대안으로 이 문제를 극복한 우도 필드 모델 likelihood field model이라는 방법에 대해서 소개하겠습니다. 이 몰델은 물리적으로 설명하기에는 부족한데, 이는 물리적인 센서 모델에 대해 조건부 확률 계산이 필요하지 않는 애드훅 알고리즘입니다. 하지만 이 방법은 잘 동작하여, 구한 사후확률은 어지러운 환경에서 더 부드럽고 계선에있어서도 효율적입니다.

 핵심 아이디어는 센서 스캔 $z_t$의 끝 점을 지도의 전역 좌표계 상에 사영시키는 것인데, 각각의 센서 측정치 $z_t^k$를 지도 m의 전역 좌표계상으로 사영하기 위해서 로봇의 좌표시스템, 센서 빔 $z_k$가 어디를 가리키는지, 어디에 존재하는지 등에 대해 알아야 합니다. 시간 t에 대한 로봇의 좌세 $x_t$ = (x y $\theta$$)^T$라 합시다. 이를 2차원 세계에서 본다면 로봇의 고정된 위치에서 센서의 상대적인 위치는 지역 좌표계로 ($x_{k, sens}$, $y_{k, sens}$$)^T$라 하고, 로봇 해딩 방향에 대한 상대적인 센서 빔의 방위를 $\theta_{k, sens}$라 하겠습니다. 이 값들은 센서에 대한 것으로 측정치 $z_t^k$의 끝점은 다음의 변환과정을 통해 전역좌표계 상에 맵핑이 됩니다.

 이 좌표계는 센서가 장애물을 감지할때만 의미가 있으며 만약 센서 거리가 최대치에 도달한다면 $z_k^t$ = $z_{max}$, 이 좌표는 물리적 세계에서 아무런 의미가 없다고 볼수 있습니다(측정 정보가 존재한다 하더라도). 우도 필드 측정 모델 likelihood field measurement model은 단순하게 최대 거리 값을 버리게 됩니다. 

 이전에 빔 모델에서 설명했던것과 마찬가지로 노이즈와 불확실성의 3가지 원인들에 대해 살펴보겠습니다.

1. 측정 노이즈 measurement noise

- 측정 과정에서 발생한 노이즈는 가우시안으로 설계할 수 있습니다. x-y 공간에서 이는 지도상에서 장애물을 찾은 경우도 포함하는데, dist는 지도 m에서 가까운 물체와 관측 좌표 ($x_{z_{t}^{k}}$, $y_{z_{t}^{k}}$$)^T$ 사이의 유클리디안 거리 euclidean distance를 의미합니다. 이 센서 측정 확률은 다음의 0평균 가우시안으로 센서 노이즈를 사용하여 정리할 수 있습니다.

그림 6.7 (a) 3 장애물이 존재하는 환경 예시(회색). 로봇은 바닥에 있으며 점선을 따라 측정 $z_t^k$를 가집니다. 

(b) 장애물 환경에 대한 우도 필드 : 검은 공간일수록 장애물을 감지할 확률이 줄어듦. 확률 p($z_t^k$ | $x_t$, m)에 대한 센서 빔은 그림 6.8에서 볼수 있음.

 그림 6.7a는 지도를 그림 6.7b는 2차원 상 관측 점 ($x_{z_{t}^{k}}$, $y_{z_{t}^{k}}$$)^T$에 대한 가우시안 우도를 보여주고 있습니다. 밝은 장소일수록 거리계가 물체가 존재한다고 측정할 가능성이 높은 장소가 됩니다. 밀도 $p_{hit}$는 센서 축과 우도 필드를 교차시킴으로서 얻을수 있는데, 여기서 센서 축은 그림 6.7의 점선입니다. 결과 함수는 그림 6.8a에서 볼 수 있습니다.

그림 6.8 (a) 그림 6.7의 상황에서 측정 $z_t^k$의 함수로 확률 $p_{hit}$($z_t^k$). 센서 빔은 점 $o_1$, $o_2$, $o_3$ 근처에서 장애물을 만남. (b) 그림 6.7 상황에서 얻을수 있는 센서 확률 p($z_t^k$ | $x_t$, m)으로 두개의 정규 분포를 추가하여 구할 수 있습니다.

2. 실패

- 최대 거리에서 구분되는 우도치를 갖는다고 가정했을때, 전에 했던것 처럼 이를 점 질량 분포 $p_{max}$로 설계할수있습니다.

3. 임의 측정 random measurement

- 마지막으로 균일 분포 $p_{rand}$를 임의의 노이즈를 설계하기 위해 사용될 수 있습니다.

 빔 기반 센서 모델처럼, 구하려는 확률 p($z_t^k$ | $x_t$, m)는 아래의 새 분포를 합쳐 구하며, 여기서도 가중치 $z_{hit}$, $z_{rand}$, $z_{max}$를 사용합니다.

 그림 6.8b는 측정 빔에 대한 결과적인 분포인 p($z_t^k$ | $x_t$, m)의 예시를 보여주는데 그림 6.8a에서 본 분포 $p_{hit}$와 분포 $p_{max}$, $p_{rand}$가 합쳐진것을 알 수 있습니다. 새로운 센서 모델을 사용하는 경우 여기서 사용되는 파라미터를 조절하여 바꿀수 있습니다. 이전 처럼 직접 보면서 할 수도 있고 ML 추정기를 사용하여 학습할수도 있습니다. 6.7b같은 표현을 우도 필드 likelihood filed라 하며, 전역 x-y좌표계의 함수로서 장애물 감지의 우도를 나타내고 있습니다.

표 6.3 가장 가까운 물체까지의 유클리디안 거리를 사용하여 거리계의 우도를 계산하는 알고리즘. 함수 prob($dist^2$, $\sigma_{hit}^{2}$)는 분산이 $\sigma_{hit}^2$를 가지는 0평균 가우시안 분포를 따르는 거리의 확률을 계산합니다.

 표 6.3은 우도 필드를 사용하여 측정 확률을 계싼하는 알고리즘을 보여주고 있습니다. 이는 센서 빔에서 서로다른 노이즈들 사이에 독립을 가정할때 p($z_t^k$ | $x_t$, m)의 각각의 값을 곱했던 것과 비슷하게 볼수 있습니다. 4번째 줄에서 센서가 만약 최대치가 된다면 이 값을 무시하겠다는 의미이고, 5 ~8번째 줄은 특이한 경우들을 처리하게 됩니다. 여기서 x-y 공간에 존재하는 가장 가까운 장애물까지의 거리를 계산하고(7번째 줄), 결과 우도를 8번째 줄에서 정규와 균일 분포를 합쳐서 계산합니다. (prob($dist^2$, $\sigma_{hit}^{2]$)는 분산이 $\sigma_{hit}^{2}$인 0평균 가우시안 분포를 따르는 $dist^2$의 확률을 계산하는 함수)

 우도 필드 거리계 모델 likelihood field range finder model 알고리즘에서 가장 큰 비용이 드는 작업은 7번줄의 지도에서 가장 가까운 물체를 찾는 것으로 이 탐색 속도를 높이기 위해선 룩업 테이블로 좌표계를 변환하여 측정 확률을 계산하는것으로 우도 필드에 대한 전계산이 유용합니다. 물론 이산 격자가 사용된다면, 룩업의 결과는 근사화 될것이고 잘못된 장애물의 좌표를 반환할 수도 있습니다. 하지만 확률 p($z_t^k$ | $x_t$, m) 영향은 일반적인 그리드에서 크지는 않습니다.

6.3.4 현실적인 고려 사항들 practical consideration

 현실적으로, 모든 센서 측정값의 밀도 계산은 꽤 시간이 걸리는 작업이 될 수 있는데, 예를 들면 레이저 스캔 데이터는 초당 수백개를 받으므로 초당 수배의 스캔 시간이 걸리게 됩니다. 각각의 스캔 빔에 대한 작업과 자세를 고려하여야 하기때문에  스캔 데이터를 현지 신뢰도에 합치는 작업은 항상 실시간으로 수행 될 수는 없습니다. 이 문제를 해결하기 위한 방법은 모든 관측치 중 일부만을 반영하는 것인데 예를 들면 360개의 레이저 스캔 데이터 데신 8개의 측정치만을 사용할 수도 있습니다. 이 방법은 중요한 이점을 갖는데, 인접한 레이저 스캔 빔은 종종 독립적이지 않기 때문에, 일부 측정치들을 버리더라도 인접한 측정치에서 노이즈에 대해 상태 추정 과정이 덜 민감하게 됩니다. 

 인접한 측정치 사이 의존성이 강할때, ML 모델은 과적합하여 덜 최적화된 결과를 나타낼 수도 있습니다. 간단한 해결방뻡중 하나로 p($z_k^k$ | $x_t$, m)을 더 약한 버전인 $\alpha$ < 1, p($z_k^k$ | $x_t$, m$)^{\alpha}$를 사용하는 것입니다. 이는 알파를 이용해 센서로부터 얻는 정보를 줄이게 됩니다. 다른 방법은 응용 분야의 환경에 맞게 고유 파라미터를 학습시키는 것으로 예를 들면, 여러 시간에 대해서 이동 로봇의 위치 추정시 좋은 위치 추정 결과를 구하는 고유 파라미터를 경사 하강법을 통해 학습하는 것이 가능합니다. 이러한 여러 시간을 사용하는 방법은 위에서 살펴본 단일 시간 ML 추정기와 상당히 다른 점이 있는데, 현실적인 측면에서 여러 시간에서 수행한 것이 더 좋은 결과를 구할 수 있습니다.

 빔 기반 모델에서 시간 소모가 가장 큰 동작은 광선 투사 ray casting 작업으로 p($z_k$ | $x_t$)를 계산하는 비용은 레이 케스팅 전처리 알고리즘과 결과를 메모리에 저장함으로서 줄일수 있는데 여기서 레이 케스팅 작업을 테이블 룩업으로 대체하게 됩니다. 이 하이디어를 구현하기 위해서 상태 공간을 3차원 낱알 형태로 분해하여야 하고 각각의 그리드 셀에 대해 거리 $z_{t}^{k*}$를 전 계산pre-compute 합니다. 여기서 그리드에 해상도에 따라 메모리 요구량이 크게 변할수 있으며 이동 로봇 위치 추정문제에서 그리드 셀의 해상도가 15cm인 2차원 문제에서 잘 동작하는것을 확인하였습니다. 이는 컴퓨터에 적합한 크기로 광선 투사를 온라인으로 구현하는데 적합한 크기가 되었습니다.

6.3.2 고유 모델 파라미터 조절하기 adjusting the intrinsic model parameter

 아직까지 센서 모델의 다양항 파라미터들을 어떻게 정하는지 다루지 않았습니다. 이 파라미터들은 $z_{hit}$, $z_{short}$, $z_{max}$, $z_{rand}$와 $\sigma_{hit}$, $\lamdba_{short}$ 등을 포함합니다. 이제 모든 고유 파라미터 집합을 $\Theta$로 부르겠습니다. 센서 측정치의 우도는 $\Theta$에 대한 함수가 됩니다.

 이 고유 파라미터를 결정하기 위한 방법으로 데이터를 사용할 수 있는데 그림 6.4가 이동 로봇이 사무실을 돌아다니면서 얻은 2종류의 측정 데이터 10,000개를 보여주고 있습니다. 두 그림다 거리 측정치를 통해 기대 거리를 3미터(2.9 ~ 3.1m 사이)로 근사시킬수 있습니다. 왼쪽 그림은 초음파 데이터, 오른쪽 그림은 레이저 데이터이며 둘다 x축은 1에서 10,000까지 읽은 데이터의 수, y축은 센서로 측정한 거리를 보여주고 있습니다. 두 센서다 대부분의 측정이 올가른 거리에 가깝게 측정되었으나 센서의 동작이 약간 다른것을 볼 수 있습니다. 초음파 센서는 노이즈와 감지 에러가 더 많이 보이며, 장애물 감지를 자주 실패하면서 최대 거리로 측정되고 있습니다. 반면에 레이저 거리계는 더 정확하지만 종종 잘못된 거리가 측정 되고 있습니다.

 고유 파라미터 $\Theta$를 설정하기 위한 방법은 이제 살펴보면, 결과 분포가 원하는 형태가 되도록 조절하거나, 원칙적인 방법은 실제 데이터들로부터 이 파라미터들을 학습시키면 됩니다. 이는 참조 데이터 집합 Z = {$z_i$}와 관련 위치 X = {x_i}, 지도 m이 주어질때 우도를 최대화 시키면 되는데, 여기서 각각의 $z_i$는 실제 측정치, $x_i$는 측정이 이루어진 자세, m은 지도를 의미합니다.

 데이터 Z의 우도는 다음과 같이 주어지며, 우리의 목표는 이 우도를 최대화 시키는 고유 파라미터 $\Theta$를 찾는것입니다. 이러한 데이터의 우도를 최대화 시키는 알고리즘을 최대 우도 추정 maximum likelihood estimator라 부르며, 줄여서 머신러닝 추정기 ML estimator라고도 할 수 있습니다.

 표 6.2는 고유 파라미터 학습 learn intrinsic parameters 알고리즘으로 고유 파라미터에 대한 최대 우도 추정을 계산하는 알고리즘입니다. 아래에서 보겠지만 이 알고리즘은 기대 최대화 알고리즘의 구현체로 ML 파라미터 추정에 반복 과정을 수행합니다. 초기에 이 고유 파라미터 학습 알고리즘은 좋은 고유치 파라미터 $\sigma_{hit}$, $\lamdba_{short}$로 초기화가 필요합니다. 

 3 ~ 9줄은 보조 변수 $e_{i, xxx}$를 추정합니다. 여기서 xxx는 센서 모델의 4가지 측면인 hit, short, max, random이고, 이 변수는 xxx에 의해 발생하는 측정치 확률입니다. 다음으로 10 ~ 15번째 줄에서 고유 파라미터들을 추정하는데, 고유 파라미터는 계산된 기대치에 대한 함수로 내부 파라미터를 조정하는것은 기대치를 변화시키므로 이 알고리즘은 여러차래 반복되어야 합니다. 하지만 현실적으로 반복은 빠르게 수행되어 12번 정도면 좋은 결과를 구하는데 충분 합니다.

- 좌측은 그림 6.4의 데이터 셋에 최대 우도 근사로 얻은 파라미터를 적용한 센서 모델을 보여주고 있습니다.

 그림 6.5는 데이터의 4가지 예시와 고유 파라미터 학습으로 계산한 ML 관측 모델을 보여주고 있씁니다. 첫번째 행은 초음파 센서로 기록한 데이터의 근사치를 보여주고, 두번째 행은 레이저 거리계를 보여주고 있습니다. 열은 실제 거리에서 차이가 나타나는데 이 데이터들은 히스토그램 형태로 정리되어 있습니다. 두 그래프 사이 명확하게 볼수있는 차이 중 하나는 거리 $z_{t}^{k*}$가 짧을수록 관측치가 더 정확한 점과 거리가 먼 것보다 짧은 것이 좁은 가우시안의 형태를 가지고 있습니다. 추가적으로 레이저 거리계가 초음파 센서보다 더 정밀한데 가우시안이 좁고 최대치로 거리가 측정된 경우의 수가 작다는 점에서 알 수 있습니다.  주의해야할 더 중요한 점은 우도가 높은 경후 측정치가 더 짧게 나옵니다. 이 큰 우도 에러는 이점과 장점을 가지고 있는데, 안 좋은 점은 장애물과 부딪힌 경우와 측정 거리 사이의 우도에서의 차이가 작기 때문에 센서 정보 일부를 읽게 됩니다. 긍정적인 점은 이 모델은 사람 처럼 로봇의 주행을 방해하는 설계되지 않은 요란들에 덜 민감하게 됩니다.

- (a) 이전에 획득한 지도에 레이저 스캔 데이터를 사영한 것. (b) 자세 $x_t$가 주어질 때, 우도 p($z_t$ | $x_t$, m)을 지도 상에 사영한 것(회색). 지점이 더 검을 수록 p($z_t$ | $x_t$, m)이 더 커지게 됨.

 그림 6.6은 동작시에 센서 모델을 보여주고 있습니다. 그림 6.6a는 180도 레이저 스캔을 보여주고 있는데 로봇은 이전에 획득한 점유 격자 지도 상에 존재합니다. 그림 6.6b는 레이저 스캔 데이터의 우도 p($z_t$ | $x_t$, m)를 x-y 공간 상에 사영시킨것을 보여주고 있습닏. 더 검은 곳일 수록 로봇이 존재할 확률이 더 커지게 됩니다. 여기서 놀라운 점은 방 안보다 복도에서 기하학적으로 높은 확률을 갖게 되는데, 이는 확률 질량이 복도를 나타내고 있으며, 로봇의 정확한 자세를 결정하기에는 불충분 하기 때문입니다. 이는 복도의 대칭성이 크기 때문이며, 로봇의 방위에 대한 정보를 알수 없기 때문에 사후확률이 2개의 좋은 통로를 따라 만들어지게 됩니다. 각각의 통로는 로봇의 해딩 방향을 나타내며 하나만 남게 됩니다

6.2 지도

 측정 값 생성 처리를 표현하기 위해 측정 치가 만들어지는 주위 환경에 대해 명시하여야 합니다. 이 주위 환경에 대한 지도는 환경에 대한 물체들의 리스트로, 지난 챕터에서 로봇 동작 모델을 개발할 때 점유된 경우를 고려하면서 살펴보았었습니다. 지도 m은 다음의 성질을 가지는 주위 환경에 대한 물체들의 목록이 됩니다.

 여기서 N은 주위 환경을 나타내는 전체 물체들의 갯수이고 각각의 $m_n$은 1 <= n <=N 으로 명시됩니다. 이 지도는 인덱싱 되는 방법이 특징 기반 방법 feature based과 위치 기반 location based 방법 2가지가 주로 사용됩니다. 특징 기반 지도에서 n은 특징의 인덱스이고, $m_n$의 값은 해당 특징의 속성으로 특징의 카티지안 좌표를 포함합니다. 위치 기반 지도에서 n은 위치를 의미하며, 평면 지도에서 $m_n$ 대신 $m_{x, y}$로 지도의 요소로 나타냅니다. $m_{x, y}$는 좌표계 (x, y)의 값을 의미합니다.

 두가지 타입의 지도 다 장점과 단점을 가지고 잇는데, 위치 기반 지도는 양적으로 volumetric, 어느 공간에 대해서도 나타낼 수 있습니다. 양적인 지도는 주위 환경에 대한 물체의 정보를 재공할 뿐만 아니라 물체의 존재 여부 정보도 포함하는데, 이는 특징 기반의 지도와는 상당히 다릅니다.

 특징 기반의 지도는 특정 장소의 환경 형태만 명시하는데, 물체의 위치만 지도상에 존재하게 됩니다. 특징 표현법은 감지한 결과와 같은 물체들의 자세를 조절하기가 쉬워, 이러한 이유로 로봇의 지도 작성 영역에서 자주 사용됩니다.  이 책에서는 두가지 지도에 대해 다루어 볼것이고 한가지 표현법에서 다른 방법으로 바꾸어서 살펴보겠습니다.

 고전적인 지도 표현 방법을 점유 격자 지도 occupancy grid map라 부르는 방법이 있는데 이에 대해서 9장에서 살펴보겠습니다. 점유 격자 지도는 위치 기반으로 x-y 자표계 각각에 2진 점유 값을 할당하여 이 위치가 물체가 존재하는지 아닌지를 나타냅니다. 점유 격자 지도는 이동 로봇 주행에서 중요하며 점유하지 않은 공간에 대해 경로를 쉽게 찾아냅니다.

 이 책 전반에서 물리적 세계와 지도 사이에 차이를 살펴볼것이고, 기술적으로 센서 측정은 물체의 지도가 아니라 물리적 물체에 의해 발생합니다. 그러나 m이 주어질때 조건부 센서 모델을 사용하는것이 일반적이므로 지도가 주어질때 측정을 사용하는 방법들을 다루어 보겠습니다

6.3 거리 측정기의 빔 모델 beam models of range finders

 거리 측정기 range finder는 로봇 공학에서 주로 사용되는 센서로, 첫번째 센서 모델로 이 거리 측정기의 물리적 모델을 근사시키겠습니다. 거리 측정기는 근처에 존재하는 물체 까지의 거리를 측정하며, 이 거리는 빔 형태로 측정되어 레이저 거리 측정기의 동작이나 초음파 센서 모델로 사용됩니다.

6.3.1 기본 측정 알고리즘 the basic measurement algorithm

 모델이 동작하도록 하기 위해서 우리가 만들 모델은 4가지 타입의 측정 에러들을 합쳐내야 합니다. 작은 측정 노이즈와 의도체 않은 물체에 의한 에러, 물체 감지 실패에 의한 에러, 임의의 알수 없는 노이즈로 구하려는 모델 p($z_t$ | $x_t$, m)은 그러므로 이 4가지 밀도를 합친것으로 이들은 각각의 특징적인 타입에 대응됩니다.

1. 거리와 지역 측정 노이즈 correct range with local measurement nosie

- 이상적인 경우 거리 측정기는 항상 물체까지의 올바른 거리를 측정할 겁니다. $z_{t}^{k*}$를 측정된 물체 $z_t^k$의 실제 거리라고 합시다. 위치 기반 지도에서 $z_{t}^{k*}$는 광선 투사로 ray casting 정해질 수 있고, 특징 기반 지도에서는 측정시 가장 가까운 특징을 찾음으로서 얻을 수 있습니다. 하지만 센서가 올바르게 가까운 거리를 측정했다면 여기서 이 값은 에러의 영향을 받습니다. 이 에러는 거리 센서의 제한된 해상도와 측정 신호가 지나가는 대기의 영향과 기타 등등으로 발생합니다. 이 노이즈는 평균이 $z_{t}^{k*}$이고표준편차가$\sigma_hit$인 좁은 가우시안 분포로 설계 할 수 있습니다. 이 가우시안을 $p_{hit}$라 하겠씁니다. 그림 6.2a는 $z_{t}^{k*}$ 값에 대한 가우시안 밀도 함수 $p_{hit}$를 보여주고 있습니다.

- 현실적으로 거리 센서로 측정한 값은 [0: $z_{max}$] 사이로 제한도기 때문에 $z_{max}$를 최대 감지 거리로 표기합니다. 그래서 측정 함수는 아래와 같이 주어지며 $x_t$, m이 주어질때 광선 투사를 통해 $z_{t}^{k*}$를 계산합니다.

 N($z_{t}^{k}$; $z_{t}^{k*}$ ; $\sigma_{hit}^{2}$)는 평균이 $z_{t}^{k*}$이고, 분산이 $\sigma_{hit}^{2}$인 단변수 정규분포로 아래와 같으며

 정규자 $\eta$는 다음과 같습니다.

 분산 $\sigma_{hit}$는 측정 모델의 내부적인 노이즈 파라미터로 이 파라미터 셋팅 방법에 대해서 아래에서 다루어보겠습니다.

2. 예상치 못한 물체들 unexpected objects

- 지도 m는 정적이지만 이동 로봇의 주위 환경이 동적인 경우, 지도에 포함되지 않은 물체들이 지도보다 비교할때 생각보다 짧은 거리들을 만들수도 있습니다. 움직이는 물체의 예시로 로봇과 동일한 공간에서 돌아다니는 사람이 될수 있고, 이러한 물체에 대처하기 위한 방법은 그들을 상태 백터에 포함시켜 위치를 추정하는 것입니다. 다른 방법으로 더 단순하게 그들을 센서 노이즈로 처리하면 됩니다. 센서 노이즈로 처리하는 경우 모델링 하지 않은 물체들은 $z_{t}^{k*}$보다 더 짧은 거리를 가지게 됩니다.

- 일반적으로 의도치 않은 물체의 측정 우도는 거리에 따라서 감소하는데 두 사람이 한 위치에 있으면 고정된 우도치가 보여질 겁니다. 한사람의 거리를 $z_1$, 다른 두번째 사람의 거리를 $z_2$라고 하고, $z_1$ < $z_2$라라고 가정해봅시다. 그러면 측정 $z_1$이 $z_2$보다 측정될 확률이 클겁니다. 첫번째 사람이 존재한다면 센서는 $z_1$을 측정할 것이지만 $z_2$를 측정하기 위해서는 첫번째 사람이 없어야만 합니다.

- 수학적으로 이러한 상황에서 거리 측정 확률을 지수 분포 exponential distribution으로 나타내는데, 이 분포의 파라미터 $\lambda_{short}$는 측정 모델의 내부 파라미터로 이 지수 분포의 정의에 따라 $p_{short}$($z_{t}^{k}$| $x_t$, m)에 대해 다음의 방정식을 얻을 수 있습니다.

- 이전 경우에서도 보았지만 지수 함수는 구간이 [0; $z_{t}^{k*}$]로 제한되므로 정규자 $\eta$가 필요하며, 이 구간에 대해 누적 확률은 다음과 같이 주어지므로

정규자 $\eta$의 값은 다음과 같이 정리할 수 있습니다.

- 그림 6.2b는 이 밀도 함수를 그래프로 표현한 것으로 밀도 함수는 거리 $z_{t}^{k}$에서 지수적으로 떨어집니다.

3. 실패

- 때때로 장애물들을 놓칠 경우가 있습니다. 예를들어 이는 초음파 센서가 기울어진 표면을 측정할때 자주 발생하는데, 레이저 거리 측정기가 빛을 흠수하는 물체나 검은 색을 감지하는 경우 또는 밝은 빛을 내는 물체를 측정하는경우도 이러한 실패가 발생합니다. 이 센서 실패의 결과는 최대 거리 측정 max-range measurement가 되어 센서는 측정 가능한 최대값 $z_{max}$를 반환합니다. 이러한 상황이 자주 발생하기 때문에 측정 모델에서 최대 거리 측정을 명시적으로 모델링 하는것이 필수적입니다.

- 이 경우에 $z_{max}$를 중심으로하는 점 질량 분포를 모델링 하겠습니다.

- 여기서 I는 매개 변수가 사실이면 1, 아니면 0을 반환하는 지시자 함수 입니다. 기술적으로 $p_{max}$는 확률 밀도 함수를 처리하지 않는데 이는 이산 분포를 따르기 때문입니다. 하지만 이 점을 걱정할 필요가 없는게 센서 측정을 다루는 수학적 모델이 밀도 함수가 존재하지 않더라도 영향을 받지 않습니다.(다이어 그램 상에 $p_{max}$를 밀도가 존재하지 않도록, $z_{max}$를 중심으로 하는 매우 낮은 균일 분포로 그렸습니다.)

4. 임의의 측정치 random measurements

- 거리 측정기는 때때로 알수없는 측정치를 측정하는데, 예를들어 소나 샌서는 벽을 벽에서 값이 튀거나 다른 센서와 크로스톡 영향을 받을때 알수없는 측정치 phatom readings를 만들어 냅니다. 이를 단순히 다루기 위해서 이런 측정치는 센서 측정 거리 전반 [0; $z_{max}$]에 대한 균일 분포를 사용하여 설계 할 수 있습니다.

- 그림 6.2d는 $p_{rand}$의 밀도 함수를 보여줍니다.

 이 내가지 서로 다른 분포들은 파라미터 $z_hit$, $z_short$, $z_max$, $z_rand$(이 파라미터들의 합은 1)를 가중치로 하여 합쳐지게 됩니다.

 이 각각의 밀도에 대한 선형 조합의 결과 밀도는 그림 6.3에서 보여주며, 점 질량 분포 $p_{max}$를 좁은 균일 분포로 나타내고 있습니다. 독자들은 4가지 기본 모델들의 특성들이 조합된 형태에서도 남아있는것을 확인할 수 있습니다.

 거리 측정 모델은 표 6.1의 빔 거리 측정 모델 beam range finder model 알고리즘을 통해 구현할수 있습니다. 이 알고리즘의 입력으로 거리 스캔 $z_t$와 로봇의 자세 $x_t$, 그리고 지도 m이 사용됩니다. 루프 밖인 2와 7번째 줄은 식 (6.2)에서 살펴보았던 개별적인 센서 빔 $z_{t}^{k}$의 우도를 곱한것이 됩니다. 4번째 줄은 특정 센서 측정치에 대해 노이즈 없는 거리를 광선 투사로 계산한 것이며, 5번째 줄에서 각각의 측정치 $z_{t}^{k}$의 우도가 식 (6.13)의 혼합 방법을 구현하여 계산됩니다. 모든 센서 측정치 $z_{t}^k$를 합친 후에 이 알고리즘은 결과 확률 p($z_t$ | $x_t$, m)을 반환하게 됩니다.

6. 관측 measurement

6.1 개요

 관측 모델은 확률 적 로봇 공학에서 동작 모델 다음으로 다룰 주요 모델로, 관측 모델은 물리적 현실에 대한 센서 관측치를 처리하는 과정을 나타냅니다. 오늘날 로봇 공학에서는 점 센서나 레이저, 카메라 등 다양한 센서들을 사용하고 있습니다. 이 모델은 센서에 의존하는데 영상 센서는 사영 기하학에 의해 가장 잘 모델되고, 소나 센서는 주위 환경 표면의 반사파나 음파를 이용하여 최적의 모델을 구할 수 있습니다.

 확률적 로봇 공학에서 센서 관측치에도 노이즈도 모델링하는데, 그 모델에서는 센서 내부에 존재하는 불확실성을 다룹니다. 관측 모델은 조건부 확률 p($z_t$ |$x_t$, m)으로 정의되는데 $x_t$는 로봇의 자세 $z_t$는 관측치, m은 주위 환경에 대한 지도가 됩니다. 이 장에서 레이저 센서 전반에 다룰것이지만 여기서 사용하는 개념과 방정식들은 이 센서에만 사용할수 있는 것이 아니고 다른 종류의 카메라나 바코드를 이용한 랜드마크 검출기 같은 센서에도 적용할 수 있습니다.

 이동 로봇이 센서로 주위 환경을 인지하는 문제를 나타내기 위해서 그림 6.1은 24개의 초음파 센서 배열이 정비된 이동로봇으로 복도에 대한 스캔 데이터를 얻은 것을 보여주고 있습니다. 각 센서에 대한 측정된 거리는 검은 선이.고, 지도의 형태는 연한 회색으로 그려지고 있습니다. 하지만 가장 가까운 물체 거리에 대한 대부분의 측정치는 해당 물체를 감지하는데 실패하였습니다. 소나는 거리 측정에 적합하지 않는것은 센서 노이즈 때문으로 볼 수 있습니다. 이 노이즈는 기술적으로 예측은 가능하나, 기울어진 표면(벽같은)에 측정시 반사파는 센서와 다른 방향으로 가버리게 되는데 이는 그림 6.1b와 같습니다. 이를 정반사 specular reflection라 부르며 더 먼 거리로 측정하게 됩니다. 정반사의 우도는 표면 물질과, 포면까지의 거리, 그리고 센서의 민감도 같은 성질에 의존하게 되는데, 다른 에러로는 쇼트리딩으로 다른 센서사이 크로스톡이나 사람 같은 설계되지 않은 물체에 의해 발생합니다.

경험으로 보건데 센서 모델이 더 정확할수록 더 좋은 결과를 구할수 있으며 이미 이 중요성을 2.4.4장에서 살펴보았습니다. 현실적으로 그러나 센서를 정확하게 설계하는것은 다음의 2가지 이유로 불가능 합니다.

 첫번째로 정확한 센서 모델 개발은 시간 소모가 크고, 두번째 이유는 정확한 모델은 우리가 모르는 상태 변수들(표면 물질)까지 필요로 합니다. 확률적 로봇공학에서는 확률적인 측면에서 센서모델의 부정확도를 수용하고 있으며, 결정론적인 함수 $z_t$ = f($x_t$) 대신 조건부 확률 밀도 p($z_t$ | $x_t$)로 측정 과정을 설계함으로써 센서 모델의 불확실성이 비결정론적인 방법으로 수용시킵니다. 여기에 기존의 로봇 공학과 다른 확률적인 기술들의 이점이 존재하며 현실적으로 정확한 모델을 사용하지 않아도 됩니다. 하지만 확률적 모델을 고안할 때 센서 측정에 영향을 주는 다른 불확실성을 다루어야 합니다.

 많은 센서들이 동작할때는 하나의 수치 측정 값보다 여러개를 만들어 냅니다. 예를 들면 카메라는 여러 배열(밝기, 세츄레이션, 색상)을 만들며, 비슷하게 레이저는 거리 스캔 데이터를 만듭니다. 이러한 센서 측정 $z_t$에 존재하는 값의 수를 K개라 한다면 다음과 같이 정리할 수 있습니다.

 $z_t^k$를 각각의 센서 측정치(하나의 거리값)으로 사용하겠는데, 그러면 이 각각의 측정 우도를 곱하여 p($z_t$ | $x_t$ , m)을 근사화 시킬수 있습니다.

 기술적으로 이것은 2.4.4에서 다루었던 마르코브 가정으로 각각의 개별적인 측정치 사이에 독립 가정을 두고 있습니다.

이 가정은 이상적인 경우에만 사실로 2.4.4장에서 노이즈가 의존적인 다양한 이유들을 살펴보았습니다.  의존성을 설명하기 위해서 거리에 대한 요소들이 존재하기 때문인데, 중간에 사람이 센서의 측정치를 방해할수도 있고 모델 m에 에러가 존재하거나 사후확률 근사시 등에서 발생 할 수있습니다. 하지만 독립 가정을 위반하더라도 크게 걱정할필요는 없고 이 문제에 대해 차후 장에서 다루어보겠습니다.

5.6 정리

 이번 장에서는 평면에서 동작하는 이동로봇의 두가지 확률적 동작 모델들을 살펴보았습니다.

- 확률적 동작 모델 p($x_t$ | $u_t$, $x_{t-1}$)에 대해 살펴보았고 여기서 고정 시간 주기 dt에 대해 제어 $u_t$는 평행 이동/회전 속도로 주어집니다. 이 모델을 구현하는데 두가지 제어 노이즈 파라미터로 평행이동과 회전 속도는 사후확률 공간을 만드는데 부족하여 3번재 노이즈 파라미터인 마지막 회전을 사용하여 표현하였습니다.

- 다른 동작 모델로 로봇의 오도메트리를 입력으로 사용하는 것을 살펴보았는데 오도메트리 측정치는 3가지 파라미터인 초기 회전, 평행이동, 마지막 회정으로 이루어져있습니다. 확률적 동작 모델은 이 세 파라미터 모두 노이즈에 영향을 받는다고 가정하여 구현하며, 오도메트리 측정치는 기술적으로는 제어가 아니지만 그 값들을 제어치로 사용하여 추정 문제에서 간편하게 사용하였습니다.

- 이 동작 모델 둘다 구현하는 방법을 살펴봤는데 하나는 p($x_t$ | $u_t$, $x_{t-1}$)를 닫힌 폼으로 계산하는것이고 하나는 p($x_t$ | $u_t$, $x_{t-1}$)로부터 샘플을 생성시키는 방법이 있습니다. 여기서 닫힌 형태 표현법은 입력 $x_t$, $u_t$, $x_{t-1}$이 사용되어 출력은 수치적은 확률 값이 됩니다. 이 확률을 계산하기 위해서 알고리즘은 제어 파라미터와 실제 치를 비교하기위해 동작 모델을 뒤집습니다. 샘플링 모델은 이러한 역변환을 요구하지는 않지만 동작 모델 p($x_t$ | $u_t$, $x_{t-1}$)의 전행 모델을 구현하며, 입력 값으로 $u_t$, $x_{t-1}$과 출력으로 p($x_t$ | $u_t$, $x_{t-1}$)를 따르는 임의의 $x_t$가 됩니다. 닫힌 형태 모델은 몇몇 확률적 알고리즘이 필요하나, 다른건 파티클 필터 같은 셈플링 모델을 사용하게 됩니다

- 마지막으로 이 모델들을 지도에 합치는 과정을 보았는데, 확률 p($x_t$ | $u_t$, $x_{t-1}$, m)은 지도 m을 조건부 확률로 합친 것으로 로봇이 존재하는지를 나타내는 지도는 자세 $x_{t-1}$에서 $x_t$ 로 이동을 시킬때 영향을 주게 됩니다. 이 확장에서는 근사화 시키며 최종 자세의 유효성을 확인하면 됩니다.

 여기서 살펴본 동작 모델들은 예시들만 존재하지만 로봇 공학 구동기 분야에서 평면 공간보다 더 넓게 다루고 있습니다. 단순히 이동 로봇 분야에서만 해도 이 모델에 다루지 못한 수많은 장치들이 있으며, 예를 들면 모든 방향으로 이동 가능한 홀로노믹 로봇 같은것도 있습니다. 여기서는 로봇 동역학을 다루지는 않지만 대부분의 로봇은 물리적 법칙을 따르고, 노이즈 파라미터로 정할수 있는 아날로그적으로 설계 됩니다.

 동역학적 모델을 다루기 위해서 기체의 동역학적 상태를 다루는 속도 벡터까지 로봇의 상태가 확장되어야 합니다. 다양한 방법으로 직관적으로 할수 있지만 이 책 범위를 넘어가므로 센서 측정에 대한 중요한 주제들을 다루어 보겠습니다. 

5.5 동작과 지도 Motion and Maps

 그동안 p($x_t$ | $u_t$, $x_{t-1}$)를 다룰때, 로봇의 동작을 외부를 고려하지 않은 사용하였습니다. 하지만 이 모델은 주변 환경에 대한 정보가 없는 경우 로봇의 동작을 나타냅니다. 하지만 많은 경우 지도 m 이 주어지며, 여기서 지도란 로봇이 주행할수 있는 공간인지 아닌지에 대한 정보를 가지고 있습니다.

 예를들어 점유격자 지도 occupancy maps(이후 챕터에서 다룸)는 공간이 점유되었는지 텅비었는지를 구분하는데, 로봇의 자세는 텅빈 공간에서만 존재하여야 합니다. 그러므로 지도 m을 아는것은 제어 $u_t$를 수행한 후에 로봇의 자세 $x_t$에 대한 추가적인 정보를 줍니다.

 이를 고려해서 지도 m이 주어질때 동작 모델을 고려하여봅시다. 이 모델을 p($x_t$ | $u_t$, $x_{t-1}$, m)으로 적을수 있는데 여기서 m은 표준변수로 추가되었씁니다. 만약 m이 자세 추정과 관련된 정보들을 제공한다면, 아래의 관계를 구할 수 있습니다.

 동작 모델 p($x_t$ | $u_t$, $x_{t-1}$, m)은 지도가 없는 동작 모델인 p($x_t$ | $u_t$, $x_{t-1}$)보다 더 나은 결과를 구할수 있습니다. 그래서 p($x_t$ | $u_t$, $x_{t-1}$, m)를 지도 기반 모션 모델 map based motion model이라 부릅니다. 이 지도기반 모션 모델은 지도 m을 가진 로봇이 자세 $x_{t-1}$에서 동작 $u_t$를 수행한 후에 자세 $x_t$에 도착하는 우도 likelihood를 계산합니다.

 불행히도 이 닫힌 형태의 동작 모델을 계산하기는 힘든 일입니다. 왜냐하면 동작 $u_t$가 수행된 후에 $x_t$에서의 우도를 계산하기 위해서, $x_{t-1}$과 $x_t$ 사이에 존재하는 비점유 경로가 존재하는 확률을 합쳐야 하고, 로봇이 동작을 수행할때 이 비점유된 경로를 따라서 움직여야 하기 때문입니다.

 다행이도 지도 기반 동작 모델을 효과율적으로 근사하는 방법이 존재하는데 이는 $x_{t-1}$과 $x_t$ 사이의 거리를 줄이는 것입니다.(로봇의 반지름 보다 작게) 이 근사화 방법은 다음의 두 가지 요소로 지도 기반 모션모델을 분해할 수 있습니다.

 여기서 $\eta$는 정규자로, 이 분해에 따르면 지도자유 추정인 p($x_t$ | $u_t$, $x_{t-1}$)에 두번째 항으로 p($x_t$ | m)을 곱하면 되는데, p($x_t$ | m)은 지도이 주어질때 자세 $x_t$의 일관성을 의미합니다.

 점유 지도의 경우에서 만약 로봇이 지도의 점유된 격자 셀에 로봇이 충돌한다면 p($x_t$ | m) = 0이 되나 그렇지 않은 경우 상수 값으로 다루겠습니다. p($x_t$ | m)과 p($x_t$ | $u_t$, $x_{t-1}$)를 곱하여 지도와 함께 자세 $x_{t-1}$에서 확률 질량을 나타내는 분포를 얻을수 있는데 위 경우가 아니라면 항상  p($x_t$ | $u_t$, $x_{t-1}$)의 형태를 가지게 됩니다. $\eta$는 정규화를 하기위해 사용될수 있으며 이 지도기반 모델의 근사는 지도 자유 동작 모델과 비교해서 큰 오버해드 없이 쉽게 계산할 수 있습니다.

표 5.7 지도 m을 활용하여  p($x_t$ | $u_t$, $x_{t-1}$, m)를 계산하는 알고리즘

  표 5.7은 지도 기반 동작 모델의 계산과 샘플링하는 기본 알고리즘을 보여주고 있습니다. 샘플링 알고리즘에서는 가중치를 가진 샘플들을 반환하는데 여기서는 중요성 가중치가 p($x_t$ | m)에 비례하고 있습니다. 이 샘플 버전을 구현하는데서는 내부 루프의 제거가 보장되어야만 합니다.

 예를들자면 그림 5.11에서의 모션모델을 보면 그림 5.11a에서의 밀도는  p($x_t$ | $u_t$, $x_{t-1}$)으로 속도 모델로 계산됩니다. 그림 5.11b는 사각형 장애물이 존재하는 지도 m을 가정하고 있는데, 로봇이 장애물과 교차하는 모든 자세 $x_t$에서 확률 p($x_t$ | m)은 0이 됩니다.

 여기서 사용할 로봇은 원형이므로 장애물은 로봇의 반지름보다 크게 이루어져 있습니다. 그림 5.11b에서 p($x_t$ | $u_t$, $x_{t-1}$, m)의 결과를 보여주는데 이 값은 p($x_t$ | m)과 p($x_t$ | $u_t$, $x_{t-1}$)의 정규화된 곱이 됩니다. p($x_t$ |  m)는 장애물이 있는 곳에서는 0이고, 모든 곳에서 p($x_t$ | $u_t$, $x_{t-1}$)에 비례하게 됩니다.

 그림 5.11은 근사화 문제를 또한 보여주고 있는데, (*)이라 표기한 영역은 p($x_t$ | $u_t$, $x_{t-1}$)과 p($x_t$ | m)에 의하여 0이 아닌 우도를 가지고 있게 됩니다. 하지만 로봇이 이 공간으로 가기 위해서 벽을 통과하여야 하지만 실제 현실에서는 불가능 합니다. 이 문제는 목적지까지 로봇의 경로 일관성을 확인하는 대신 마지막 자세 $x_{t-1}$에서의 일관성을 확인한 결과이지만 현실적으로 이러한 에러는 큰 동작 $u_t$에서만 발생하지, 갱신 주기가 큰 경우에 무시해도 됩니다.

 근사시 발생하는 이 문제를 없에기 위해선 식 (5.48)에 베이즈룰을 적용하여 다음이 됩니다.

 p(m | $x_t$, $u_t$, $x_{t-1}$)를 p(m | $x_t$로 근사화 시킨다면 다시 한번 베이즈룰을 통해 다음과 같이 정리할 수 있습니다.

여기서 $\eta$는 정규자(서로다른 변환 단계 이 값들은 다릅니다.)이며, 이 간단한 분석을 통해 지도 기반 모델을 러프하게 정리할 수 있습니다.

 이 식은 같지는 않지만, m이 주어질때 조건부 확률을 계산하는 경우 근사 시에 $u_t$, $x_t$항을 생략하고, 이들을 생략함으로서 $x_t$를 향하는 로봇의 경로 관련 정보들을 읽어버리게 됩니다. 위 예제로 이러한 생략의 결과를 봤는데 여기서 벽 뒤의 자세들은 0이 아닌 우도치를 가지는것을 보았습니다. 이러한 지도 기반 동작 모델의 근사치는 초기와 마지막 위치가 점유되지 않은 공간이며 벽을 통과했다고 잘못 가정한 것을수도 있지만  어떻게 이 문제를 해결할까요? 위에서 살펴봤듯이 이는 갱신 간격에 의존하므로 갱신 주기를 높이면 이 효과가 발생하지 않은체 충분한 근사치를 구할수 있게됩니다.

5.4.2 샘플링 알고리즘 sampling algorithm

 위치 추정 문제에서 파티클 필터를 사용한다면 p($x_t$ | $u_t$, $x_{t-1}$)로 샘플링을 수행할겁니다. 4.2.1에서는 p($x_t$ | $u_t$, $x_{t-1}$)를 계산하기 보다는 p($x_t$ | $u_t$, $x_{t-1}$)의샘플을사용했는데,  표 5.6의샘플 모션 모델 오도메트리 알고리즘은 샘플링 방법을 구현한것이 됩니다. 초기 자세 $x_{t-1}$과 오도메트리 값 $u_t$를 입력으로 하고, 출력은 p($x_t$ | $u_t$, $x_{t-1}$)를 따르는 $x_t$의 분포가 됩니다. 이전의 알고리즘과 차이점은 주어진 $x_t$에 대한 확률을 계산하는것이 아닌 자세 $x_t$를 추정을 수행합니다(5 ~ 10번째 줄). 샘플 모션 오도메트리 알고리즘은 역 모델의 필요성을 피하므로, 모션 모델 오도메트리 알고리즘보다 구현하기는 쉽습니다.

 그림 5.9는 샘플 모션 모델 오도메트리로 생성한 샘플들의 예시로 그림 5.8의 모델과 같은 파라미터를 사용하였습니다.

 그림 5.10은 여러 시간에 걸친 샘플 집합들로 모션 모델을 보여주고 있습니다. 이 데이터는 파티클 필터 알고리즘의 동작 갱신 방정식을 사용하여 생성되었는데 오도메트리는 로봇의 경로인 실선을 따르도록 되어잇습니다. 이 그림은 로봇이 움직일 수록 불확실성이 커지는 것을 보여주며, 샘플들이 더 넓은 공간으로 퍼지게 됩니다.

5.4 오도메트리 동작 모델 odometry motion model

 앞서 살펴본 속도 동작 모델은 로봇의 속도를 사용하여 자세애 대한 사후확률을 계산하였습니다. 이외에도 로봇의 동작을 계산하는 오도메트리 측정 값을 사용할 수도 있는데, 오도메트리는 휠 인코더 정보를 적분하여 얻으며, 대부분의 상업용 로봇은 그러한 벙법으로 자세 추정이 가능합니다. 현실적으로 오도메트리는 여전히 에러가 크나 속도보다는 정교합니다. 드리프트와 미끄러짐이 발생하기는 하나 속도는 실제 속도기와 수학적 속도 모델 사이의 차이 또한 존재하나, 오도메트리는 로봇이 움직인 후에만 얻을수 있어 필터 알고리즘에 대해 문제가 되지 않습니다. 하지만 정확한 동작 계획과 제어에서는 사용될수가 없습니다.

5.4.1 닫힌 형태의 계산 Closed Form Calculation

 이번 장에서는 제어 입력으로 오도메트리 측정 값을 사용하는 동작 모델을 정의하겠습니다. 기술적으로 오도메트리는 제어가 아닌 센서 측정값인데 오도메트리를 측정으로 설계하기 위해서 베이즈 필터는 상태 변수로 실제 속도를 포함시켜야 합니다. 상태 공간을 작게 나둔다면 오도메트리를 제어 신호로 사용하는 방법이 흔하게 사용됩니다. 이번 장에서는 오도메트리 측정치를 제어 입력으로 다루어보고 이를 통해 구한 모델들은 오늘날 최고의 확률적 로봇 시스템의 핵심이 됩니다.

 우선 제어 정보의 형태를 정의하면 시간 t에 대해 로봇의 자세는 확률 변수 $x_t$로 하고, 로봇의 오도메트리는 이 자세를 추정하게 됩니다. 하지만 드리프트와 밀림 때문에 실제 물리적 세계와 로봇의 내부 오도메트리 좌표계 사이에는 고정된 좌표계간 변환은 없습니다. 이 변환은 로봇의 위치 추정 문제를 해결합니다.

 오도메트리 모델은 로봇의 내부 오도메트리의 상대적인 정보들을 사용하는데, 자세히 보면 구간 (t-1, t]에서 자세 $x_{t-1}$에서 $x_t$로 로봇이 전진하면 오도메트리는 이 전진에 대해 $\bar{x_{t-1}}$ = ($\bar{x}$ $\bar{y}$ $bar{\theta}$)에서 $\bar{x_t}$ = ($\bar{x}'$ $\bar{y}$' $\bar{\theta}$')를 전달합니다. 여기서 바는 이 값들이 오도메트리 측정치로 알수 없는 전역 좌표계 상에 존재하는 로봇 내부 좌표계를 따르게 됩니다. 상태 추정에서 이 정보를 사용하기 위해서 $\bar_{x_{t-1}}$과 $\bar{x_t}$사이의 차이를 사용하며 이 차이는 실제 자세 $x_{t-1}$과 $x_t$의 차이에 대한 좋은 근사치가 됩니다. 동작 정보 $u_t$는 그래서 다음과 같이 주어지며

- 위 오도메트리 모델은 구간 (t-1, t]에서의 로봇 동작으로 회전 $\delta_{rot1}$, 평행이동 $\delta_{trans}$, 두번쨰 회전 $\delta_{rot2}$로 근사화되며, 회전과 평행이동에서 노이즈가 존재합니다.

 상대적인 오도메트리를 구하기 위해 $u_t$는 다음의 3가지 단계로 변환됩니다. 회전, 평행 이동 동작, 그리고 다른 회전 등. 그림 5.7은 이 과정을 나놔서 보여주고 있는데 초기 회전량을 $\detal_{rot1}$이라 하고, 이동을 $\delta_{trans}$ 그리고 다음 회전 치를 $\delta_{rot2}$라 합니다. 여기서 자세 ($\bar{s}$ $\bar{s}$')사이에는 파라미터 벡터인 ($\delta_{rot1}$ $\delta_{trans}$ $\delta_{rot2}$$)^T$를 가지며 이 파라미터들은 $\bar{s}$, $\bar{s}$'사이의 상대적인 동작을 나타냅니다. 그래서 $\delta_{rot1}$, $\delta_{trans}$, $\delta_{rot2}$는오도메트리로 엔코드된 상대적인 동작이 됩니다. 우리가 사용할 동작 모델은 이 세 파라미터는 노이즈에 영향을 받으며 이전 장에서 살펴본 속도 벡터보다 더 자주 사용하겠습니다.

표 5.5 오도메트리 정보 기반 p($x_t$ | $u_t$, $x_{t-1}$)을 계산하는 알고리즘

- 시간 t에 대해 자세를  $x_{t-1}$ = (x y $\theta$$)^T$로 구하는데, 제어 입력은 로봇의 오도메트리 정보 $u_t$ = ($\bar{x_{t-1}}$ $\bar{x_t}$$)^T$로 구한 두 자세 사이의 차이가 사용됩니다. 여기서 $\bar{x_{t-1}}$ = ($\bar{x}$ $\bar{y}$ $\bar{theta}$), $\bar{x_t}$ = ($\bar{x}$' $\bar{y}$' $\bar{\theta}$')

 수학적으로 자세한 사항들을 살펴보기 전에 이 닫힌 형태의 밀도 함수를 계산하는 기본 알고리즘에 대해 살펴보겠습니다. 표 5.5는 오도메트리로부터 p($x_t$ | $u_t$, $x_{t-1}$)를 계산하는 기본 알고리즘으로 이 알고리즘은 입력으로 초기 위치 $x_{t-1}$, 오도메트리로 구한 자세 쌍 $u_t$ = ($\bar{x_{t-1}}$, $\bar{x_t}$$)^T$, 가정 최종 자세 $x_t$를 사용하며, 확률 p($x_t$ | $u_t$, $x_{t-1}$)가 출력이 됩니다.

 이 알고리즘을 자세히 다뤄보면 2~4번째 줄은 상대적인 모션 파라미터인 ($\delta_{rot1}$ $\delta_{trans}$ $\delta_{rot2}$$)^T$를 오도메트리 정보로 부터 복원하는 과정으로, 이를 이용해 역 동작 모델 inverse motion model을 구현합니다. 실제 자세 $x_{t-1}$, $x_t$ 사이의 상대적인 동작인 ($\hat{delta_{rot1}}$ $\hat{delta_{trans}}$ $\hat{delta_{rot2}}$$)^T$는 5~7번째 줄 사이에서 계산됩니다. 8~10번째 줄 사이에는 각 모션 파라미터의 에러 확률을 계산하는데 위에서 보았듯이 함수 prob(a, b)는 평균이 0이고 분산이 b인 분포의 a에 대한 값을 의미하며 여기서 범위는 [-$\pi$, $\pi$]가 됩니다. $delta_2$ - $\bar_{delta_2}$의 결과는 이 모델이 사용된 소프트웨어에 따라 에러에 차이가 존재하게 됩니다. 마지막으로 11번째 줄은 이 에러 확률들을 곱하여 결과를 반환합니다. 이 마지막 단계는 에러들 사이에 독립이라고 가정한 것으로 $\alpha_1$ ~ $\alpha_4$는 로봇의 동작 노이즈를 명시하는 파라미터가 됩니다.

 그림 5.8은 에러 파라미터 $\alpha_1$ ~ $\alpha_4$를 설정함에 따라 오도메트리 동작 모델의 예시들을 보여줍니다. 그림 5.8a 분포는 프로토 타입으로 5.8b, 5.8c는 평행이동이나 회전 에러가 더 큰경우를 보여주고 있습니다.  이미 그림 5.3에서 비슷한 그림을 보았지만 측정하는 시간 사이가 짧을수록 이 동작 모델의 차이는 더 비슷해질겁니다. 그래서 신뢰도가 더 자주 갱신된다면 동작 모델사이의 차이는 더 줄어들게 됩니다. 일반적으로 오도메트리 모델이 속도 모델보다 더 주로 선호되는데 오도메터가 속도 제어기보다 더 정확하기 때문입니다.