6.6.3 알려진 대응관계를 가진 센서모델 sensor model with known correspondence
이 측정모델을 구현하기 위해서 특징 $f_t^i$와 랜드마크 $m_j$ 사이의 대응 관계를 만드는 변수를 정의하여야 합니다. 이 변수는 $c_t^i$로 표기하며 $c_t^i$ $\in$ {1, . . ., N+1}; N은 지도 m에 존재하는 랜드마크의 개수가 됩니다. $c_t^i$ = j <= N이면, 시간 t에서 관측되는 i번째 특징은 j번째 랜드마크에 대응하게 됩니다. 다시말하면 $c_t^i$는 관측된 특징의 실제 아이디가 됩니다. 예외상황은 $c_t^i$ = N + 1일때 생기는데 특징 관측시 지도 m상에 대응하는 특징이 존재하지 않는 경우로, 이 때 잘못된 랜드마크를 다루는것이 매우 중요합니다. 지난번에 관측되지 않은 랜드마크를 다룬 로봇 맵핑 주제와 큰 연관성을 가지고 있습니다.

표 6.4 랜드마크 관측 우도를 계산하는 알고리즘. 이 알고리즘은 입력으로 관측된 특징 $f_t^i$ = ($r_t^i$ $\phi_t^i$ $s_t^i$$)^T$와 실제 특징의 아이디 $c_t^i$, 로봇의 자세 $x_t$ = (x y $\theta$$)^T$와 지도 m이 사용되며, 출력은 확률 p($f_t^i$ | $c_t^i$, m, $x_t$)가 됩니다.
표 6.4는 특징 $f_t^i$가 알려진 대응관계 $c_t^i$에대한 확률을 계산하는 알고리즘으로 3,4 번재줄은 랜드마크 까지 실제 거리와 방위를 계산합니다. 측정된 거리와 방위에 대한 확률은 5번째 줄에서 수행되는데 노이즈에 독립으로 가정합니다. 이 알고리즘은 식 (6.41)에서 쉽게 볼수 있습니다.
6.6.4 자세 샘플링 sampling poses
특징 아이디 $c_t^i$인 측정 특징 $f_t^i$에 일치하는 로봇 자세 $x_t$를 샘플하는것이 바람직 한 경우가 있습니다. 이미 로봇의 동작 모델을 다루던 이전 장에서 샘플링 알고리즘들을 살펴보았습니다. 그 샘플링모델들을 센서 모델에도 적용할 수 있는데, 로봇을 전역적으로 위치를 추정할 때, 로봇 자세에 대한 초기 추정을 만들기 위해 센서 측정치를 통합한 샘플 자세들을 만드는것이 효율적입니다.
일반적인 경우에 센서 관측 $z_t$에 대응하는 자세 $x_t$를 샘플링 하는것은 효율적인 샘플링 알고리즘을 사용할 랜드마크 모델에서는 어렵습니다. 하지만 그러한 샘플링은 추가적인 가정을 따르는 경우에 가능한데, 사전 확률 p($x_t$ | $c_t^i$, m)을 알아야만 합니다. 쉽게 얘기하면 이 사전 확률은 균일하다고 가정하면 베이즈 정리는 다음과 같이 구할 수 있습니다.
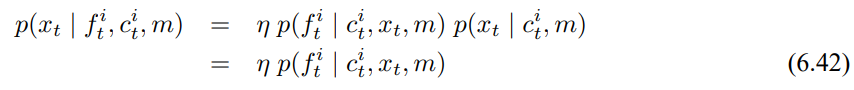

표 6.5 랜드마크 측정 $f_t^i$ = ($r_t^i$ $\phi_t^i$ $s_t^i$$)^T$과 알려진 아이디 $c_t^i$가 주어질때 자세 샘플링 알고리즘
p($x_t$ | $f_t^i$, $c_t^i$, m)로부터 샘플링은 역 센서 모델 p($f_t^i$ | $c_t^i$, $x_t$, m)으로부터 구할 수 있는데 표 6.5가 자세 $x_t$를 샘플링하는 알고리즘을 보여주고 있습니다. 노이즈의 영향을 받지 않는 경우에도 랜드마크 관측치는 유일하게 로봇의 위치를 결정하지 못합니다. 대신, 로봇은 랜드마크까지의 거리를 반지름으로 하는 주위에 원의 형태로 로봇이 존재할 수 있습니다. 이 로봇 자세의 비결정성은 거리와 방위가 3차원 공간상에 로봇의 자세에 대해 2가지 제약조건을 주는것으로부터 알수 있습니다.
이 자세 추정기를 구현하기 위해서 랜드마크 주위 원에서 로봇이 어디있는지를 결정하는 자유 파라미터를 샘플해야합니다. 이 파라미터는 표 6.5에서 $\hat{\gamma}$로 보릅니다. 그리고 3, 4, 5번째 줄에서 가우시안을 따르는 분포에 의해 측정된 거리와 방위가 바뀌게 됩니다. 마지막으로 6 ~8번째줄에서 $\hat{\gamma}$, $\hat{r}$, $\hat{\phi}$에 대한 자세를 복원하는 과정을 수행합니다.
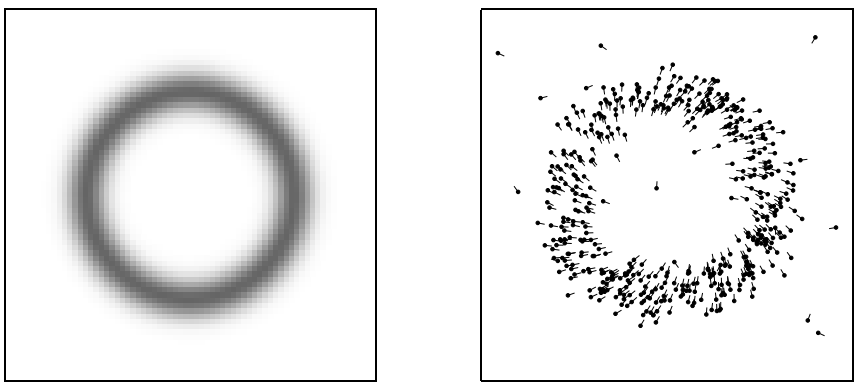
그림 6.12 랜드마크 감지 모델: (a) 로봇의 자세에서 5m거리에 30도(2차원 상으로 사영됨)로 랜드마크 감지되었을때 사후확률 분포. (b) 이 감지시 생성된 로봇 자세 샘플들. 선은 자세의 방향을 알려줌.
그림 6.12는 왼쪽 다이어그램이 자세 분포 p($x_t$ | $f_t^i$, $c_t^i$, m)과 오른쪽 다이어그램 대응관계가 알려진 샘플 랜드 마크 모델 알고리즘 sample landmark model known correspondence을 사용한 샘플들을 보여줍니다. 사후확률은 xy공간상에 사영되어 측정 거리 $r_t^i$로 인해 원형 모양이 됩니다. 3차원 공간에서는 각 $\theta$에 따라 접혀지지 않은 나선 링의 형태가 됩니다.
'번역 > 구)확률적로봇공학' 카테고리의 다른 글
| 확률적 로봇 공학 - 7. 이동 로봇 위치 추정 (0) | 2020.06.24 |
|---|---|
| 확률적 로봇 공학 - 6.6.5~ 추가적인 고려사항들 (0) | 2020.06.24 |
| 확률적 로봇 공학 - 6.6 특징 기반 센서 모델 (0) | 2020.06.24 |
| 확률적 로봇 공학 - 6.4.2 우도 필드 추가사항 (0) | 2020.06.24 |
| 확률적 로봇 공학 - 6.4 거리계에 대한 우도 필드 (0) | 2020.06.23 |