확률적 로봇 공학 - 5.4.2 오도메트리 동작 모델 샘플링 알고리즘

 

5.4.2 샘플링 알고리즘 sampling algorithm

표 5.6 오도메트리 정보를 이용한 샘플링 알고리즘

 위치 추정 문제에서 파티클 필터를 사용한다면 p($x_t$ | $u_t$, $x_{t-1}$)로 샘플링을 수행할겁니다. 4.2.1에서는 p($x_t$ | $u_t$, $x_{t-1}$)를 계산하기 보다는 p($x_t$ | $u_t$, $x_{t-1}$)의샘플을사용했는데,  표 5.6의샘플 모션 모델 오도메트리 알고리즘은 샘플링 방법을 구현한것이 됩니다. 초기 자세 $x_{t-1}$과 오도메트리 값 $u_t$를 입력으로 하고, 출력은 p($x_t$ | $u_t$, $x_{t-1}$)를 따르는 $x_t$의 분포가 됩니다. 이전의 알고리즘과 차이점은 주어진 $x_t$에 대한 확률을 계산하는것이 아닌 자세 $x_t$를 추정을 수행합니다(5 ~ 10번째 줄). 샘플 모션 오도메트리 알고리즘은 역 모델의 필요성을 피하므로, 모션 모델 오도메트리 알고리즘보다 구현하기는 쉽습니다.

 

그림 5.9 오도메트리 모션 모델로부터 샘플링. 그림 5.8과 동일한 파라미터를 사용하였고 각그림은 500개의 샘플들을 사용.

 

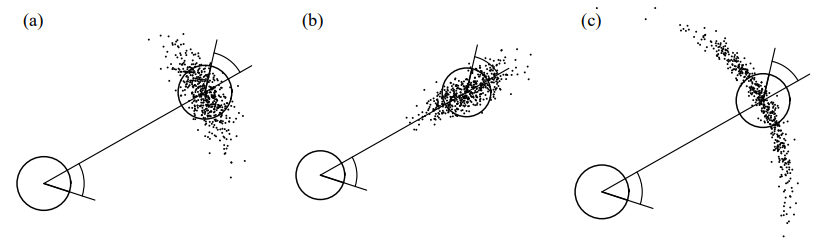
 그림 5.9는 샘플 모션 모델 오도메트리로 생성한 샘플들의 예시로 그림 5.8의 모델과 같은 파라미터를 사용하였습니다.

 

그림 5.10 무센서 로봇의 자세 사후확률 샘플링 근사. 실선은 동작이고, 시간 마다 샘플들은 다른 형태로 로봇의 신뢰드를 보여줌

 

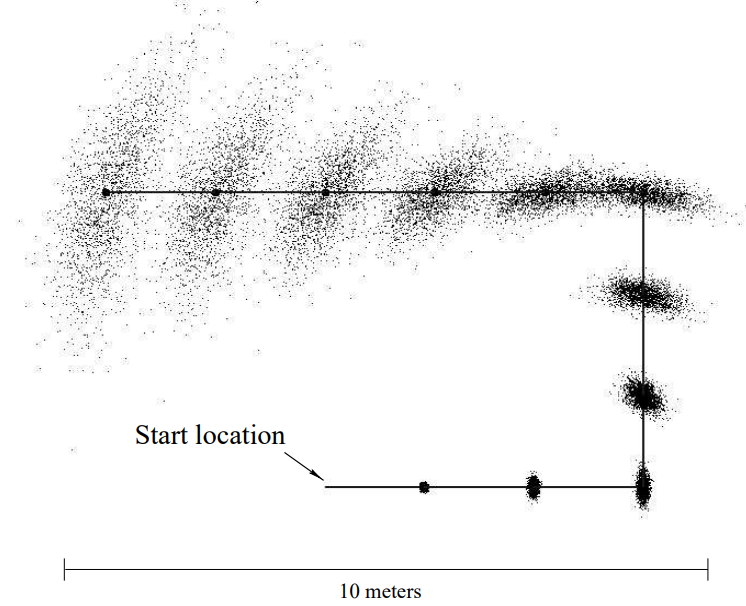
 그림 5.10은 여러 시간에 걸친 샘플 집합들로 모션 모델을 보여주고 있습니다. 이 데이터는 파티클 필터 알고리즘의 동작 갱신 방정식을 사용하여 생성되었는데 오도메트리는 로봇의 경로인 실선을 따르도록 되어잇습니다. 이 그림은 로봇이 움직일 수록 불확실성이 커지는 것을 보여주며, 샘플들이 더 넓은 공간으로 퍼지게 됩니다.